人教版数学八年级下册 18.1 平行四边形 同步练习含答案
文档属性
| 名称 | 人教版数学八年级下册 18.1 平行四边形 同步练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 116.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 13:33:43 | ||
图片预览


文档简介
平行四边形
同步练习
一、选择题
1、不能判断四边形ABCD是平行四边形的是(???
)
A.AB=CD,AD=BC?????
B.AB=CD,AB∥CD
C.AB=CD,AD∥BC?????D.AB∥CD,AD∥BC
2、在□ABCD中,∠A:∠B:∠C:∠D的值可能是(???
)
A.1:2:3:4
??????
B
.1:2:2:1
??????
C
.2:2:1:1
???????
D
.2:1:2:1
3、下面给出了四边形ABCD中∠A、∠B、∠C、∠D的度数之比,其中能判定四边形ABCD是平行四边形的是(???
)
A.1∶2∶3∶4?????
B.2∶2∶3∶3?????????
C.2∶3∶3∶2?????
D.2∶3∶2∶3
4、平行四边形的一条边长为12cm,那么这个平行四边形的两条对角线的长可以是(???
)
A.5
cm
和7
cm??
B.20
cm
和30
cm??
C.8
cm
和16
cm??
D.6
cm和10
cm
5、如图,在ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形(???
)
A.AE=CF???????
B.DE=BF
C.∠ADE=∠CBF??????
D.∠AED=∠CFB
6、如图,以□ABCD对角线的交点为坐标原点,以平行于AD边的直线为x轴,建立平面直角坐标系.若点D的坐标为(3,2),则点B的坐标为( )
?
A.(-3,-2)??
?
B.(2,3)???
C.(-2,-3)???????
D.(3,2)
7、如图,在四边形ABCD中,E是BC边的中点,连结DE并延长,交AB的延长线于F点,.添加一个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是( )A.???
?
B.?????
C.??
?
D.
8、将一张平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积.则这样的折纸方法共有( )
A、1种???????
B、2种???????
C、4种???????
D、无数种
9、如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AE于点F,则∠1=( )
A、40°
B、50°
C、60°
D、80°
10、□ABCD的周长为36
cm,AB=BC,则较长边的长为(???
)
A.15
cm?
???????B.7.5
cm?
??????C.10.5
cm??
??D.21
cm
11、已知:如图,在□ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF
于G、H,并有下列结论:(1)BE=DF;?
(2)AG=GH=HC;?
(3)EG=BG;?
(4)S△ABE=3
S△AGE.其中正确的结论有(???
)
(A)1个???????
(B)2个????
(C)3个???????
(D)4个
12、根据如图所示的(1),(2),(3)三个图所表示的规律,依次下去第个图中平行四边形的个数是(???
)
A.3n??????
B.3n(n+1)?????
C.6n??????
D.6n(n+1)
2、填空题
13、如图所示,在ABCD中,E,F分别是对角线BD上的两点,且BE=DF,要证明四边形AECF是平行四边形,最简单的方法是根据???????????
来证明.
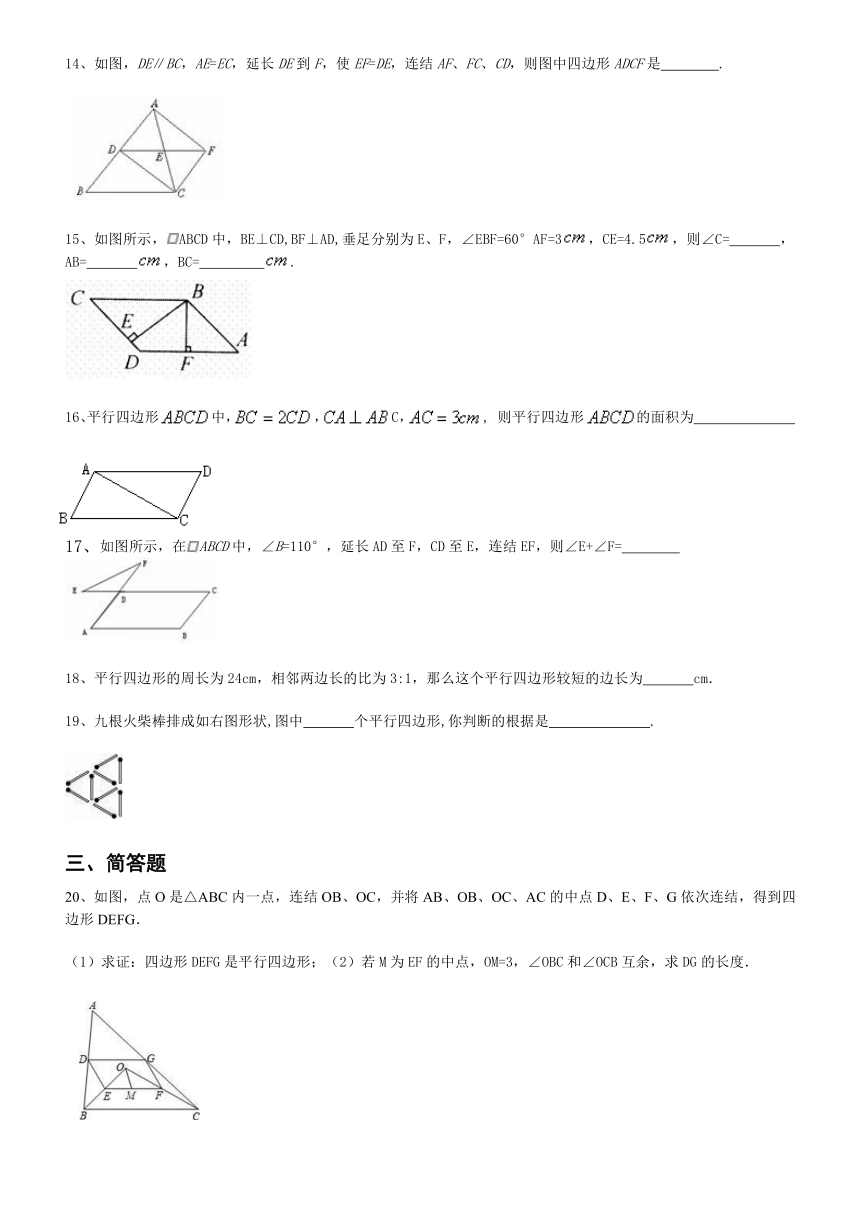
14、如图,DE∥BC,AE=EC,延长DE到F,使EF=DE,连结AF、FC、CD,则图中四边形ADCF是????.
15、如图所示,ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,∠EBF=60°AF=3,CE=4.5,则∠C=???
,AB=???
,BC=????
.?
16、平行四边形中,,C,,
则平行四边形的面积为???????
17、如图所示,在ABCD中,∠B=110°,延长AD至F,CD至E,连结EF,则∠E+∠F=????
18、平行四边形的周长为24cm,相邻两边长的比为3:1,那么这个平行四边形较短的边长为?
cm.
19、九根火柴棒排成如右图形状,图中?
个平行四边形,你判断的根据是?
?
.
3、简答题
20、如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
?
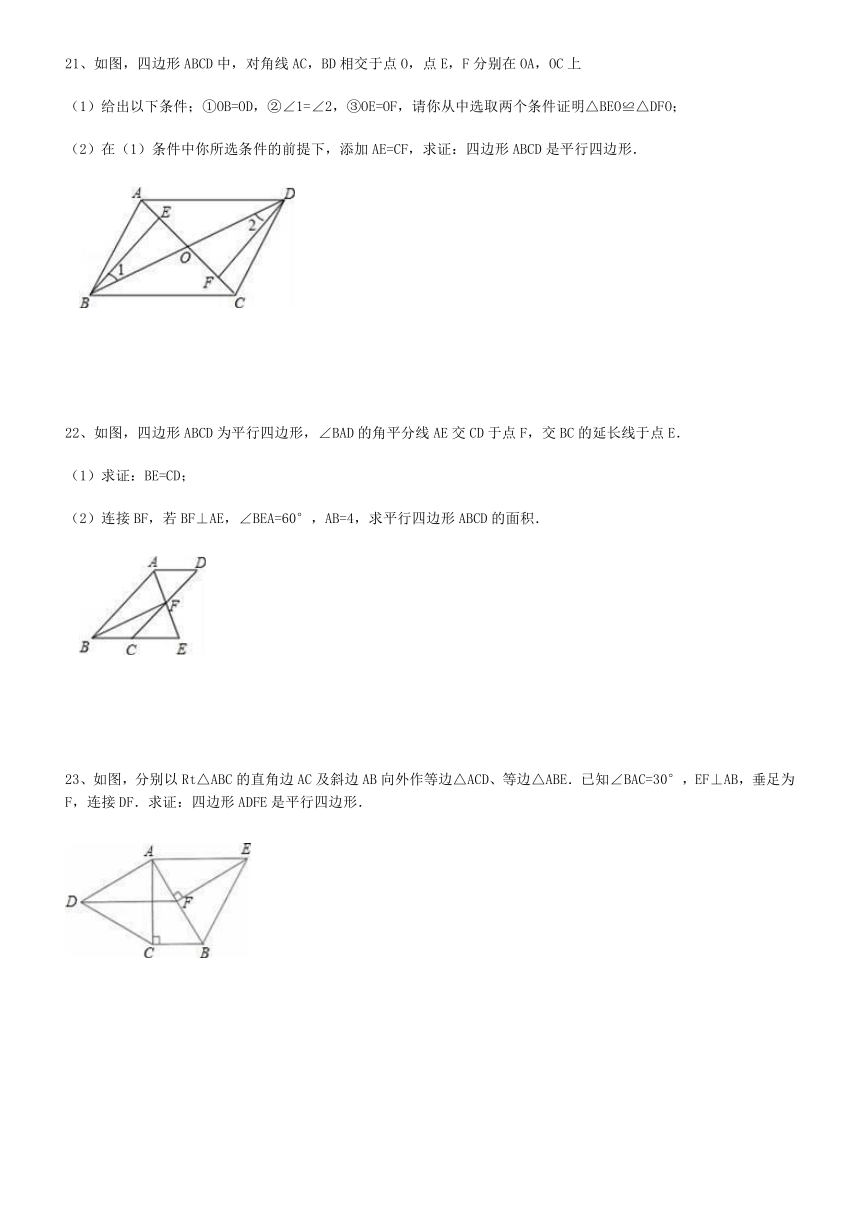
21、如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.
?
22、如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
?
23、如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.求证:四边形ADFE是平行四边形.
24、如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.
(1)求证:BE=DF;
(2)求证:AF∥CE.
25、如图1,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点P是对角线BD上的一点,PQ∥BA交AD于点Q,PS∥BC交DC于点S,四边形PQRS是平行四边形。
(1)当点P与点B重合时,图1变为图2,若∠ABD=90°,求证:△ABR≌△CRD;
(2)对于图1,若四边形PRDS也是平行四边形,此时,你能推出四边形ABCD还应满足什么条件?
参考答案
一、选择题
1、C;2、D;3、D;4、B;5、B;6、A;7、D;8、D;9、B;10、C;11、D.;12、B;
二、填空题
13、对角线互相平分;
14、平行四边形;
15、30°,6,9;
16、;
17、70°
18、3
19、有3?
两组对边分别相等的四边形是平行四边形
三、简答题
20、解:(1)∵D、G分别是AB、AC的中点,
∴DG∥BC,DG=BC,
∵E、F分别是OB、OC的中点,
∴EF∥BC,EF=
BC,
∴DG=EF,DG∥EF,
∴四边形DEFG是平行四边形;
(2)∵∠OBC和∠OCB互余,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∵M为EF的中点,OM=3,
∴EF=2OM=6.
由(1)有四边形DEFG是平行四边形,
∴DG=EF=6.
21、证明:(1)选取①②,
∵在△BEO和△DFO中
,
∴△BEO≌△DFO(ASA);
(2)由(1)得:△BEO≌△DFO,
∴EO=FO,BO=DO,
∵AE=CF,
∴AO=CO,
∴四边形ABCD是平行四边形.
22、解:四边形ABFC是平行四边形;理由如下:
∵AB∥CD,
∴∠BAE=∠CFE,
∵E是BC的中点,
∴BE=CE,
在△ABE和△FCE中,
,
∴△ABE≌△FCE(AAS);
∴AE=EF,
又∵BE=CE
∴四边形ABFC是平行四边形.
23、证明:在Rt△ABC,∠BAC=30°,
∴∠ABC=60°,
等边△ABE中,∠ABE=60°,且AB=BE,
∵EF⊥AB,
∴∠EFB=90°,
∴Rt△ABC≌Rt△EBF,
∴AC=EF,
又在等边△ACD中,∠DAC=60°,AD=AC,
又∵∠BAC=30°,
∴∠DAF=90°,
∴AD∥EF,
又∵AC=EF,∴AD=EF,
∴四边形ADFE是平行四边形.
24、(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠5=∠3,
∵∠1=∠2,
∴∠AEB=∠4,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF;
(2)由(1)得△ABE≌△CDF,
∴AE=CF,
∵∠1=∠2,
∴AE∥CF,
∴四边形AECF是平行四边形,
∴AF∥CE.
25、(1)证明:∵∠ABD=90°,AB∥CR,∴CR⊥BD
∵BC=CD,
∴∠BCR=∠DCR
∵四边形ABCR是平行四边形,
∴∠BCR=∠BAR∴∠BAR=∠DCR
又∵AB=CR,AR=BC=CD,∴△ABR≌△CRD
(2)由PS∥QR,PS∥RD知,点R在QD上,故BC∥AD。
又由AB=CD知∠A=∠CDA
因为SR∥PQ∥BA,
所以∠SRD=∠A=∠CDA,从而SR=SD。
由PS∥BC及BC=CD知SP=SD。而SP=DR,所以SR=SD=RD?
故∠CDA=60°。
因此四边形ABCD还应满足BC∥AD,∠CDA=60°
(注:若推出的条件为BC∥AD,∠BAD=60°或BC∥AD,∠BCD=120°等亦可。)
同步练习
一、选择题
1、不能判断四边形ABCD是平行四边形的是(???
)
A.AB=CD,AD=BC?????
B.AB=CD,AB∥CD
C.AB=CD,AD∥BC?????D.AB∥CD,AD∥BC
2、在□ABCD中,∠A:∠B:∠C:∠D的值可能是(???
)
A.1:2:3:4
??????
B
.1:2:2:1
??????
C
.2:2:1:1
???????
D
.2:1:2:1
3、下面给出了四边形ABCD中∠A、∠B、∠C、∠D的度数之比,其中能判定四边形ABCD是平行四边形的是(???
)
A.1∶2∶3∶4?????
B.2∶2∶3∶3?????????
C.2∶3∶3∶2?????
D.2∶3∶2∶3
4、平行四边形的一条边长为12cm,那么这个平行四边形的两条对角线的长可以是(???
)
A.5
cm
和7
cm??
B.20
cm
和30
cm??
C.8
cm
和16
cm??
D.6
cm和10
cm
5、如图,在ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形(???
)
A.AE=CF???????
B.DE=BF
C.∠ADE=∠CBF??????
D.∠AED=∠CFB
6、如图,以□ABCD对角线的交点为坐标原点,以平行于AD边的直线为x轴,建立平面直角坐标系.若点D的坐标为(3,2),则点B的坐标为( )
?
A.(-3,-2)??
?
B.(2,3)???
C.(-2,-3)???????
D.(3,2)
7、如图,在四边形ABCD中,E是BC边的中点,连结DE并延长,交AB的延长线于F点,.添加一个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是( )A.???
?
B.?????
C.??
?
D.
8、将一张平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积.则这样的折纸方法共有( )
A、1种???????
B、2种???????
C、4种???????
D、无数种
9、如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AE于点F,则∠1=( )
A、40°
B、50°
C、60°
D、80°
10、□ABCD的周长为36
cm,AB=BC,则较长边的长为(???
)
A.15
cm?
???????B.7.5
cm?
??????C.10.5
cm??
??D.21
cm
11、已知:如图,在□ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF
于G、H,并有下列结论:(1)BE=DF;?
(2)AG=GH=HC;?
(3)EG=BG;?
(4)S△ABE=3
S△AGE.其中正确的结论有(???
)
(A)1个???????
(B)2个????
(C)3个???????
(D)4个
12、根据如图所示的(1),(2),(3)三个图所表示的规律,依次下去第个图中平行四边形的个数是(???
)
A.3n??????
B.3n(n+1)?????
C.6n??????
D.6n(n+1)
2、填空题
13、如图所示,在ABCD中,E,F分别是对角线BD上的两点,且BE=DF,要证明四边形AECF是平行四边形,最简单的方法是根据???????????
来证明.
14、如图,DE∥BC,AE=EC,延长DE到F,使EF=DE,连结AF、FC、CD,则图中四边形ADCF是????.
15、如图所示,ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,∠EBF=60°AF=3,CE=4.5,则∠C=???
,AB=???
,BC=????
.?
16、平行四边形中,,C,,
则平行四边形的面积为???????
17、如图所示,在ABCD中,∠B=110°,延长AD至F,CD至E,连结EF,则∠E+∠F=????
18、平行四边形的周长为24cm,相邻两边长的比为3:1,那么这个平行四边形较短的边长为?
cm.
19、九根火柴棒排成如右图形状,图中?
个平行四边形,你判断的根据是?
?
.
3、简答题
20、如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
?
21、如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.
?
22、如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
?
23、如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.求证:四边形ADFE是平行四边形.
24、如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.
(1)求证:BE=DF;
(2)求证:AF∥CE.
25、如图1,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点P是对角线BD上的一点,PQ∥BA交AD于点Q,PS∥BC交DC于点S,四边形PQRS是平行四边形。
(1)当点P与点B重合时,图1变为图2,若∠ABD=90°,求证:△ABR≌△CRD;
(2)对于图1,若四边形PRDS也是平行四边形,此时,你能推出四边形ABCD还应满足什么条件?
参考答案
一、选择题
1、C;2、D;3、D;4、B;5、B;6、A;7、D;8、D;9、B;10、C;11、D.;12、B;
二、填空题
13、对角线互相平分;
14、平行四边形;
15、30°,6,9;
16、;
17、70°
18、3
19、有3?
两组对边分别相等的四边形是平行四边形
三、简答题
20、解:(1)∵D、G分别是AB、AC的中点,
∴DG∥BC,DG=BC,
∵E、F分别是OB、OC的中点,
∴EF∥BC,EF=
BC,
∴DG=EF,DG∥EF,
∴四边形DEFG是平行四边形;
(2)∵∠OBC和∠OCB互余,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∵M为EF的中点,OM=3,
∴EF=2OM=6.
由(1)有四边形DEFG是平行四边形,
∴DG=EF=6.
21、证明:(1)选取①②,
∵在△BEO和△DFO中
,
∴△BEO≌△DFO(ASA);
(2)由(1)得:△BEO≌△DFO,
∴EO=FO,BO=DO,
∵AE=CF,
∴AO=CO,
∴四边形ABCD是平行四边形.
22、解:四边形ABFC是平行四边形;理由如下:
∵AB∥CD,
∴∠BAE=∠CFE,
∵E是BC的中点,
∴BE=CE,
在△ABE和△FCE中,
,
∴△ABE≌△FCE(AAS);
∴AE=EF,
又∵BE=CE
∴四边形ABFC是平行四边形.
23、证明:在Rt△ABC,∠BAC=30°,
∴∠ABC=60°,
等边△ABE中,∠ABE=60°,且AB=BE,
∵EF⊥AB,
∴∠EFB=90°,
∴Rt△ABC≌Rt△EBF,
∴AC=EF,
又在等边△ACD中,∠DAC=60°,AD=AC,
又∵∠BAC=30°,
∴∠DAF=90°,
∴AD∥EF,
又∵AC=EF,∴AD=EF,
∴四边形ADFE是平行四边形.
24、(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠5=∠3,
∵∠1=∠2,
∴∠AEB=∠4,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF;
(2)由(1)得△ABE≌△CDF,
∴AE=CF,
∵∠1=∠2,
∴AE∥CF,
∴四边形AECF是平行四边形,
∴AF∥CE.
25、(1)证明:∵∠ABD=90°,AB∥CR,∴CR⊥BD
∵BC=CD,
∴∠BCR=∠DCR
∵四边形ABCR是平行四边形,
∴∠BCR=∠BAR∴∠BAR=∠DCR
又∵AB=CR,AR=BC=CD,∴△ABR≌△CRD
(2)由PS∥QR,PS∥RD知,点R在QD上,故BC∥AD。
又由AB=CD知∠A=∠CDA
因为SR∥PQ∥BA,
所以∠SRD=∠A=∠CDA,从而SR=SD。
由PS∥BC及BC=CD知SP=SD。而SP=DR,所以SR=SD=RD?
故∠CDA=60°。
因此四边形ABCD还应满足BC∥AD,∠CDA=60°
(注:若推出的条件为BC∥AD,∠BAD=60°或BC∥AD,∠BCD=120°等亦可。)
