人教A版高中数学必修四第三章《三角恒等变换》单元测试(word有答案)
文档属性
| 名称 | 人教A版高中数学必修四第三章《三角恒等变换》单元测试(word有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 657.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 17:09:20 | ||
图片预览
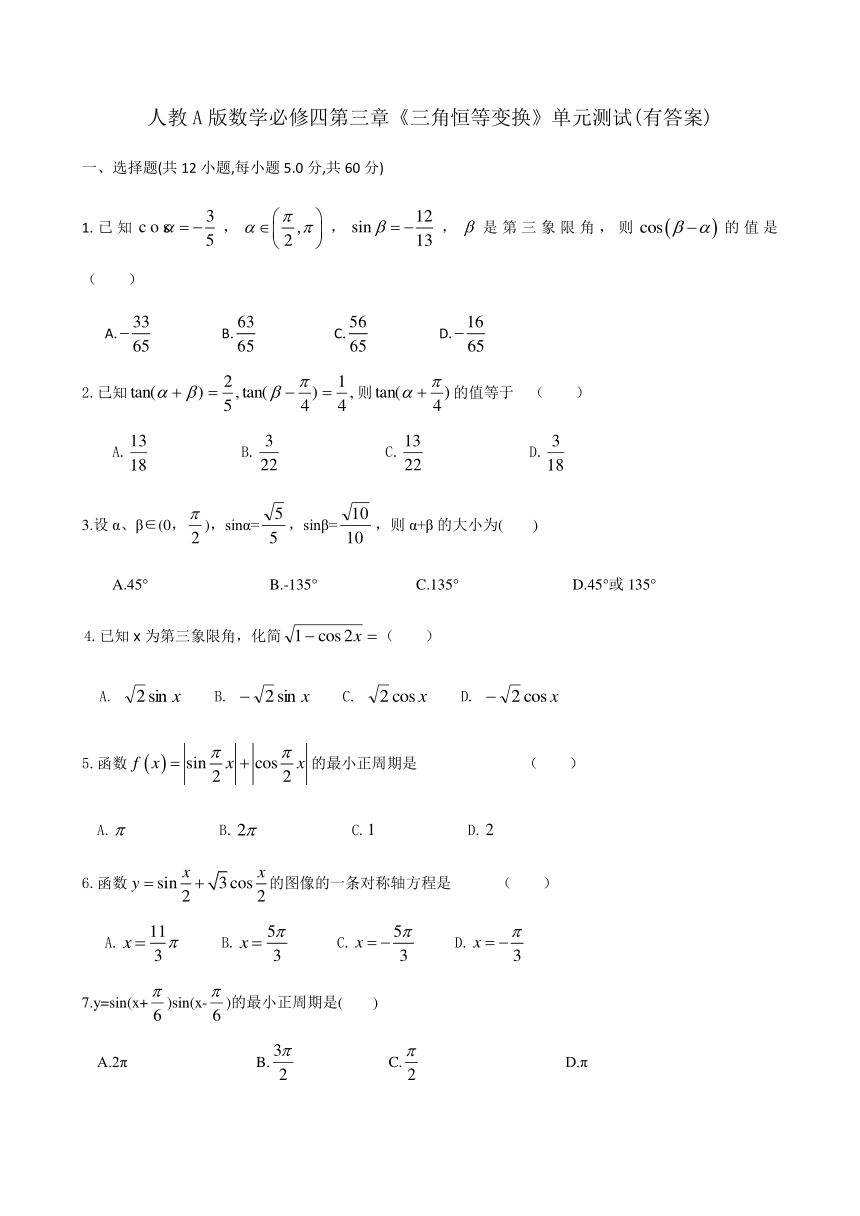



文档简介
人教A版数学必修四第三章《三角恒等变换》单元测试(有答案)
一、选择题(共12小题,每小题5.0分,共60分)
1.已知,,,是第三象限角,则的值是
(
)
A.
B.
C.
D.
2.已知则的值等于
(
)
A.
B.
C.
D.
3.设α、β∈(0,),sinα=,sinβ=,则α+β的大小为(
)
A.45°
B.-135°
C.135°
D.45°或135°
4.已知x为第三象限角,化简(
)
A.
B.
C.
D.
5.函数的最小正周期是
(
)
A.
B.
C.
D.
6.函数的图像的一条对称轴方程是
(
)
A.
B.
C.
D.
7.y=sin(x+)sin(x-)的最小正周期是(
)
A.2π
B.
C.
D.π
8.已知等腰三角形顶角的余弦值等于,则这个三角形底角的正弦值为(
)
A.
B.
C.
D.
9.已知,则(
)
A.
B.
C.
D.
10.函数y=cos2(x-)+sin2(x+)-1是(
)
A.周期为π的奇函数
B.周期为2π的偶函数
C.周期为2π的奇函数
D.周期为π的偶函数
11.已知,且,则(
)
A.2
B.
C.3
D.
12.已知不等式对于任意的恒成立,则实数的取值范围是
(
)
A.
B.
C.
D.
二、填空题(共4小题,每小题5.0分,共20分)
13.求值:_____________
14.函数的最小值是
15.已知,给出以下四个命题:
①若,则;
②直线是函数图象的一条对称轴;
③在区间上函数是增函数;
④函数的图象可由的图象向右平移个单位而得到,
其中正确命题的序号为。
16.设当时,函数取得最大值,则______
三、解答题(共7小题,共70分)
17.在锐角△ABC中,b=2,B=,,求△ABC的面积.
18.△ABC中,已知.
19.将一块圆心角为60°,半径为20cm的扇形铁电裁成一个矩形,求裁得矩形的最大面积.
20.已知函数,.
(1)求证的小正周期和最值;
(2)求这个函数的单调递增区间.
21.已知向量=(cosɑ,sinɑ),ɑ∈[-π,0].向量p=(2,1),q=(0,-),且p⊥(-q).
(1)求向量;
(2)若cos(β-π)=,0<β<π,求cos(2ɑ-β)的值.
22.如图,设A是单位圆和x轴正半轴的交点.P,Q是单位圆上两点,O是坐标原点,且∠AOP=,∠AOQ=ɑ,α∈[0,).
(1)若点Q的坐标是(,),求cos(ɑ-)的值;
(2)设函数f(ɑ)=·,求f(ɑ)的值域.
23.
设函数的图象过点P(0,1),且
的最大值是2,最小值为-2,其中.
(1)求表达式;
(2)若射线图象交点的横坐标,由小到大依次为
求的值.
【注】:部分版本教材不同,运用到等差数列相关公式可由教师决定是否告知。
参考答案
1.A
2.B
3.A
4.A
5.C
6.C
7.D
8.B
9.D
10.D
11.A
12.D
13.
14.
15.②④
16.
17.解:∵,
∴
(?http:?/??/?www.ks5u.com?/??),
∴,,
又∵为锐角,∴,∴△ABC为等边三角形,面积为.
19.如图设,则PN=,
SMNPQ=,
当时,
SMNPQ取最大值.
20(1)
(2)因为函数的单调递增区间为,
由(1)知,故
故函数的单调递增区间为
21.(1)∵=(cosα,sinα),
∴-n=(cosα,sinα+).
∵m⊥(-n),∴m·(-n)=0,
∴2cosα+sinα+=0.①
又sin2α+cos2α=1,②
由①②得sinα=-,cosα=-,∴=(-,-).
(2)∵cos(β-π)=,∴cosβ=-.
又∵0<β<π,∴sinβ==.
又∵sin
2α=2sinαcosα=2×(-)×(-)=,cos
2α=2cos2α-1=2×-1=,
∴cos(2α-β)=cos
2αcosβ+sin
2αsinβ=×(-)+×==.
注意:已知两三角函数中的隐藏条件
22.(1)由已知可得cosα=,sinα=.所以cos(α-)=cosαcos+sinαsin=×+×=.
(2)f(α)=·=(cos,sin)·(cosα,sinα)=cosα+sinα=sin(α+).
因为α∈[0,π),则α+∈[,),
所以-<sin(α+)≤1,
所以f(α)的值域是(-,1].
23.(1)
(2)由题意,知
即
的等差数列
一、选择题(共12小题,每小题5.0分,共60分)
1.已知,,,是第三象限角,则的值是
(
)
A.
B.
C.
D.
2.已知则的值等于
(
)
A.
B.
C.
D.
3.设α、β∈(0,),sinα=,sinβ=,则α+β的大小为(
)
A.45°
B.-135°
C.135°
D.45°或135°
4.已知x为第三象限角,化简(
)
A.
B.
C.
D.
5.函数的最小正周期是
(
)
A.
B.
C.
D.
6.函数的图像的一条对称轴方程是
(
)
A.
B.
C.
D.
7.y=sin(x+)sin(x-)的最小正周期是(
)
A.2π
B.
C.
D.π
8.已知等腰三角形顶角的余弦值等于,则这个三角形底角的正弦值为(
)
A.
B.
C.
D.
9.已知,则(
)
A.
B.
C.
D.
10.函数y=cos2(x-)+sin2(x+)-1是(
)
A.周期为π的奇函数
B.周期为2π的偶函数
C.周期为2π的奇函数
D.周期为π的偶函数
11.已知,且,则(
)
A.2
B.
C.3
D.
12.已知不等式对于任意的恒成立,则实数的取值范围是
(
)
A.
B.
C.
D.
二、填空题(共4小题,每小题5.0分,共20分)
13.求值:_____________
14.函数的最小值是
15.已知,给出以下四个命题:
①若,则;
②直线是函数图象的一条对称轴;
③在区间上函数是增函数;
④函数的图象可由的图象向右平移个单位而得到,
其中正确命题的序号为。
16.设当时,函数取得最大值,则______
三、解答题(共7小题,共70分)
17.在锐角△ABC中,b=2,B=,,求△ABC的面积.
18.△ABC中,已知.
19.将一块圆心角为60°,半径为20cm的扇形铁电裁成一个矩形,求裁得矩形的最大面积.
20.已知函数,.
(1)求证的小正周期和最值;
(2)求这个函数的单调递增区间.
21.已知向量=(cosɑ,sinɑ),ɑ∈[-π,0].向量p=(2,1),q=(0,-),且p⊥(-q).
(1)求向量;
(2)若cos(β-π)=,0<β<π,求cos(2ɑ-β)的值.
22.如图,设A是单位圆和x轴正半轴的交点.P,Q是单位圆上两点,O是坐标原点,且∠AOP=,∠AOQ=ɑ,α∈[0,).
(1)若点Q的坐标是(,),求cos(ɑ-)的值;
(2)设函数f(ɑ)=·,求f(ɑ)的值域.
23.
设函数的图象过点P(0,1),且
的最大值是2,最小值为-2,其中.
(1)求表达式;
(2)若射线图象交点的横坐标,由小到大依次为
求的值.
【注】:部分版本教材不同,运用到等差数列相关公式可由教师决定是否告知。
参考答案
1.A
2.B
3.A
4.A
5.C
6.C
7.D
8.B
9.D
10.D
11.A
12.D
13.
14.
15.②④
16.
17.解:∵,
∴
(?http:?/??/?www.ks5u.com?/??),
∴,,
又∵为锐角,∴,∴△ABC为等边三角形,面积为.
19.如图设,则PN=,
SMNPQ=,
当时,
SMNPQ取最大值.
20(1)
(2)因为函数的单调递增区间为,
由(1)知,故
故函数的单调递增区间为
21.(1)∵=(cosα,sinα),
∴-n=(cosα,sinα+).
∵m⊥(-n),∴m·(-n)=0,
∴2cosα+sinα+=0.①
又sin2α+cos2α=1,②
由①②得sinα=-,cosα=-,∴=(-,-).
(2)∵cos(β-π)=,∴cosβ=-.
又∵0<β<π,∴sinβ==.
又∵sin
2α=2sinαcosα=2×(-)×(-)=,cos
2α=2cos2α-1=2×-1=,
∴cos(2α-β)=cos
2αcosβ+sin
2αsinβ=×(-)+×==.
注意:已知两三角函数中的隐藏条件
22.(1)由已知可得cosα=,sinα=.所以cos(α-)=cosαcos+sinαsin=×+×=.
(2)f(α)=·=(cos,sin)·(cosα,sinα)=cosα+sinα=sin(α+).
因为α∈[0,π),则α+∈[,),
所以-<sin(α+)≤1,
所以f(α)的值域是(-,1].
23.(1)
(2)由题意,知
即
的等差数列
