人教版高一物理必修2第六章万有引力与航天——万有引力定律及其相关应用
文档属性
| 名称 | 人教版高一物理必修2第六章万有引力与航天——万有引力定律及其相关应用 |  | |
| 格式 | zip | ||
| 文件大小 | 687.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-11 16:12:29 | ||
图片预览




文档简介
万有引力定律及其相关应用——习题课
1.万有引力定律
1.在物理学发展的过程中,许多物理学家的科学研究推动了人类文明的进程.在对以下几位物理学家所作科学贡献的叙述中,正确的说法是(
)
A.英国物理学家牛顿用实验的方法测出万有引力常量G
B.第谷接受了哥白尼日心说的观点,并根据开普勒对行星运动观察记录的数据,应用严密的数学运算和椭圆轨道假说,得出了开普勒行星运动定律
C.亚里士多德认为两个从同一高度自由落下的物体,重物体与轻物体下落一样快
D.胡克认为只有在一定的条件下,弹簧的弹力才与弹簧的形变量成正比
【答案】D
【解析】牛顿在前人(如第谷、开普勒、笛卡尔等)研究的基础上,借助自己的力学成就总结出万有引力定律;1798年,即在牛顿发现万有引力定律一百多年以后,英国物理学家卡文迪许用扭秤实验证明万有引力定律是正确的,并测出万有引力恒量,选项A错误;开普勒对第谷长期天文观察的结果进行了创造性的研究与思考,开始他想用哥白尼的太阳系模型说明火星的运行轨道,但与第谷的观测结果有8分的误差,从而大胆地摒弃了天体做匀速圆周运动的观点,建立了开普勒定律,对行星的运动作出了更科学、更精确的描述,选项B错误;亚里士多德认为两个从同一高度自由落下的物体,物体越重下落越快,选项C错误;显然,选项D正确。
2.苹果落向地球,而不是地球向上碰到苹果,对此论断的正确解释是( )
A.由于地球质量比苹果质量大得多,地球对苹果的引力比苹果对地球的引力大得多造成的
B.由于地球对苹果的引力作用,而苹果对地球无引力作用造成的
C.由于苹果对地球的引力和地球对苹果的引力大小相等,但地球的质量远远大于苹果,地球不能产生明显的加速度
D.以上解释都不对
【答案】C
【解析】苹果与地球之间的吸引力是相互的,它们大小相等;在相同的力作用下,质量越大物体加速度越小,选项C正确。
3.地球可近似看成球形,由于地球表面上物体都随地球自转,所以有( )
A.物体在赤道处受的地球引力等于两极处,而重力小于两极处
B.赤道处的角速度比南纬30°大
C.地球上物体的向心加速度都指向地心,且赤道上物体的向心加速度比两极处大
D.地面上的物体随地球自转时提供向心力的是重力
【答案】A
【解析】由F=G可知,物体在地球表面任何位置受到地球的引力都相等,此引力的两个分力一个是物体的重力,另一个是物体随地球自转的向心力.在赤道上,向心力最大,重力最小,选项A正确;地表各处的角速度均等于地球自转的角速度,选项B错误;地球上只有赤道上的物体向心加速度指向地心,其他位置的向心加速度均不指向地心,选项C错误;地面上物体随地球自转的向心力是万有引力与地面支持力的合力,选项D错误.
4.牛顿以天体之间普遍存在着引力为依据,运用严密的逻辑推理,建立了万有引力定律.在创建万有引力定律的过程中,牛顿(
)
A.接受了胡克等科学家关于“吸引力与两中心距离的平方成反比”的猜想
B.根据地球上一切物体都以相同加速度下落的事实,得出物体受地球的引力与其质量成正比,即F∝m的结论
C.根据F∝m和牛顿第三定律,分析了地月间的引力关系,进而得出F∝m1m2
D.根据大量实验数据得出了比例系数G的大小
【答案】A、B.
【解析】在创建万有引力定律的过程中,牛顿接受了平方反比猜想,和物体受地球的引力与其质量成正比,即F∝m的结论,而提出万有引力定律.后来卡文迪许利用扭秤测量出万有引力常量G的大小,只有选项C是在建立万有引力定律后才进行的探索,因此符合题意的只有选项A、B.
5.地球可近似看成球形,由于地球表面上物体都随地球自转,所以有( )
A.物体在赤道处受的地球引力等于两极处,而重力小于两极处
B.赤道处的角速度比南纬30°大
C.地球上物体的向心加速度都指向地心,且赤道上物体的向心加速度比两极处大
D.地面上的物体随地球自转时提供向心力的是重力
【答案】A
【解析】由F=G可知,物体在地球表面任何位置受到地球的引力都相等,此引力的两个分力一个是物体的重力,另一个是物体随地球自转的向心力.在赤道上,向心力最大,重力最小,A对.地表各处的角速度均等于地球自转的角速度,B错.地球上只有赤道上的物体向心加速度指向地心,其他位置的向心加速度均不指向地心,C错.地面上物体随地球自转的向心力是万有引力与地面支持力的合力,D错.
6.两艘质量各为1×107kg的轮船相距100m时,它们之间的万有引力相当于( )
A.一个人的重力量级
B.一个鸡蛋的重力量级
C.一个西瓜的重力量级
D.一头牛的重力量级
【答案】B
【解析】由F引=G得F引=0.667N相当于一个鸡蛋的重力量级.
7.据报道,最近在太阳系外发现了首颗“宜居”行星,其质量约为地球质量的6.4倍,一个在地球表面重量为600N的人在这个行星表面的重量将变为960N.由此可推知,该行星的半径与地球半径之比约为( )
A.0.5
B.2
C.3.2
D.4
【答案】B
【解析】若地球质量为M0,则“宜居”行星质量为M=6.4M0,由mg=G得:=·=,所以===2.
8.1990年5月,紫金山天文台将他们发现的第2
752号小行星命名为吴健雄星,该小行星的半径为16
km.若将此小行星和地球均看成质量分布均匀的球体,小行星密度与地球相同.已知地球半径R=6
400
km,地球表面重力加速度为g.这个小行星表面的重力加速度为( )
A.400g B.g C.20g D.g
【答案】B
【解析】质量分布均匀的球体的密度ρ=3M/4πR3,地球表面的重力加速度g=GM/R2=,吴健雄星表面的重力加速度g′=GM/r2=,g/g′=R/r=400,g′=g,故选项B正确.
9.假设地球是一半径为R、质量分布均匀的球体。一矿井深度为d。已知质量分布均匀的球壳对壳内物体的引力为零。矿井底部和地面处的重力加速度大小之比为(
)
A.
B.
C.
D.
【答案】A
【解析】物体在地面上时的重力加速度可由得出。根据题中条件,球壳对其内部物体的引力为零,可认为矿井部分为一质量均匀球壳,
故矿井底部处重力加速度可由得出,故
10.位于贵州的“中国天眼”(FAST)是目前世界上口径最大的单天线射电望远镜,通过FAST可以测量地球与木星之间的距离.当FAST接收到来自木星的光线传播方向恰好与地球公转线速度方向相同时,测得地球与木星的距离是地球与太阳距离的k倍.若地球和木星绕太阳的运动均视为匀速圆周运动且轨道共面,则可知木星的公转周期为(
)
A.
年
B.
年
C.
年
D.
年
【答案】B
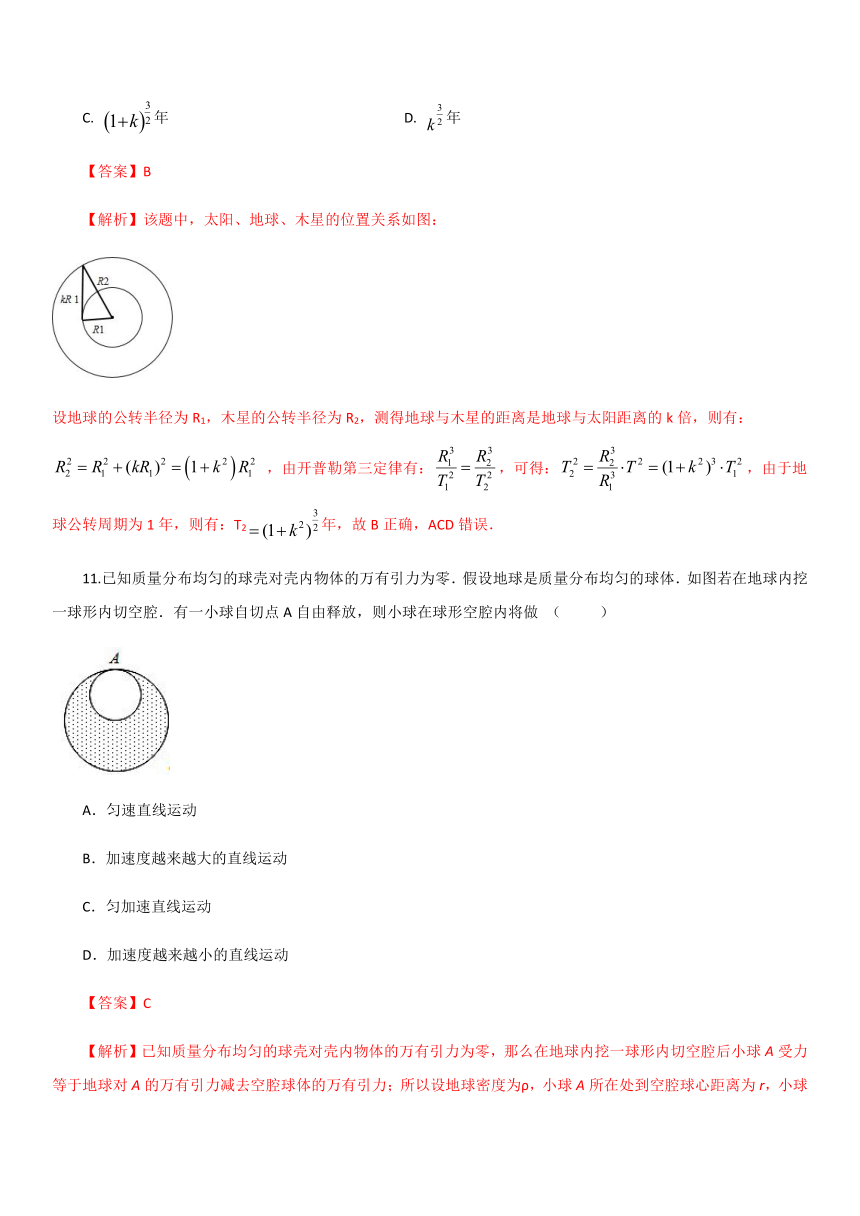
【解析】该题中,太阳、地球、木星的位置关系如图:
设地球的公转半径为R1,木星的公转半径为R2,测得地球与木星的距离是地球与太阳距离的k倍,则有:
,由开普勒第三定律有:,可得:,由于地球公转周期为1年,则有:T2年,故B正确,ACD错误.
11.已知质量分布均匀的球壳对壳内物体的万有引力为零.假设地球是质量分布均匀的球体.如图若在地球内挖一球形内切空腔.有一小球自切点A自由释放,则小球在球形空腔内将做
(
)
A.匀速直线运动
B.加速度越来越大的直线运动
C.匀加速直线运动
D.加速度越来越小的直线运动
【答案】C
【解析】已知质量分布均匀的球壳对壳内物体的万有引力为零,那么在地球内挖一球形内切空腔后小球A受力等于地球对A的万有引力减去空腔球体的万有引力;所以设地球密度为ρ,小球A所在处到空腔球心距离为r,小球A到地球中心距离为R,则R-r为两球心的距离,那么小球A受到的合外力
那么小球受到的加速度,所以小球向球心运动,加速度不变,即小球在球形空腔内将做匀加速直线运动,C正确,ACD错误。故选C
12.在一次测定引力常量的实验里,已知一个质量是0.50kg的球.以2.6×10-10N的力吸引另一个质量是12.8×10-3kg的球.这两个球相距4.0×10-2m,地球表面的重力加速度是9.8m/s2,地球直径是12.8×103km.根据这些数据计算引力常量.
【答案】6.5×10-11N·m2/kg2
【解析】对两球应用万有引力定律,由F=G
得:G==N·m2/kg2=6.5×10-11N·m2/kg2
13.你受太阳的引力是多大?和你受地球的引力比较一下,可得出什么样的结论?太阳的质量是1.99×1030
kg,地球到太阳的距离为1.5×1011m,设你的质量是60
kg.
【答案】见解析
【解析】地球半径为6.4×106
m,与地球到太阳的距离1.5×1011
m相比相差近10万倍,因此人距太阳的距离可以认为也是1.5×1011m.故人受太阳的引力F=G=6.67×10-11×N=0.35N
人受地球的引力F′=mg=60×9.8
N=588
N
==1
680
即地球对人的引力要比太阳对人的引力大一千六百多倍,所以平时计算时可以不考虑人受太阳的万有引力.
14.一物体在地球表面时重16N,它在以5m/s2的加速度上升的火箭中的视重为9N,则此时火箭离地球表面的距离为地球半径的多少倍?(g取10m/s2)
【答案】3R
【解析】设物体视重为9N时,所在位置第三重力加速度为g’,火箭对物体的支持力FN即等于物体的视重9N。对物体应用牛顿第二定律,有:,故,
解得。
由?可得:?,
从而火箭离地球表面的距离为:???。
15.火星质量是地球质量的0.1倍,半径是地球半径的0.5倍,火星被认为是除地球之外最可能有水(有生命)的星球.在经历了4.8亿公里星际旅行的美国火星探测器“勇气”号成功在火星表面上着陆,据介绍,“勇气”号在进入火星大气层之前的速度大约是声速的1.6倍,为了保证“勇气”号安全着陆,科学家给它配备了隔热舱、降落伞、减速火箭和气囊等.进入火星大气层后,先后在不同的时刻,探测器上的降落伞打开,气囊开始充气、减速火箭点火.当探测器在着陆前3s时,探测器的速度减为零,此时,降落伞的绳子被切断,探测器自由落下,求探测器自由下落的高度.假设地球和火星均为球体,由于火星的气压只有地球的大气压强的1%,则探测器所受阻力可忽略不计.(取地球表面的重力加速度g=10m/s2)
【答案】18m
【解析】设地球质量为M地,火星质量为M火,地球半径为R地,火星半径为R火,地球表面处的重力加速度为g地,火星表面处的重力加速度为g火,根据万有引力定律:
物体在地球表面上时有G=mg地①
同理,物体在火星表面上时有G=mg火②
由①÷②得:=()2=×22=0.4
g火=0.4×g地=4m/s2
由题意知,探测器在着陆前3s时开始做自由落体运动,设探测器自由下落的高度为h,则:
h=g火t2=×4×32m=18m.
2.万有引力定律的应用
1.第一宇宙速度是物体在地球表面附近环绕地球做匀速圆周运动的速度,则有( )
A.被发射的物体质量越大,第一宇宙速度越大
B.被发射的物体质量越小,第一宇宙速度越大
C.第一宇宙速度与被发射物体的质量无关
D.第一宇宙速度与地球的质量有关
【答案】 CD
【解析】第一宇宙速度v=
与地球质量M有关,与被发射物体的质量无关.
2.2003年8月29日,火星、地球和太阳处于三点一线,上演“火星冲日”的天象奇观.这是6万年来火星距地球最近的一次,与地球之间的距离只有5576万公里,为人类研究火星提供了最佳时机.如图所示为美国宇航局最新公布的“火星冲日”的虚拟图,则有( )
A.2003年8月29日,火星的线速度大于地球的线速度
B.2003年8月29日,火星的线速度小于地球的线速度
C.2004年8月29日,火星又回到了该位置
D.2004年8月29日,火星还没有回到该位置
【答案】BD
【解析】火星和地球均绕太阳做匀速圆周运动G=m可得:v=,所以轨道半径较大的火星线速度小,B正确;火星轨道半径大,线速度小,火星运动的周期较大,所以一年后地球回到该位置,而火星则还没有回到,D正确.
3.土星外层上有一个环,为了判断它是土星的一部分还是土星的卫星群,可以测量环中各层的线速度v与该层到土星中心的距离R之间的关系来判断( )
A.若v∝R,则该层是土星的一部分
B.若v2∝R,则该层是土星的卫星群
C.若v∝,则该层是土星的一部分
D.若v2∝,则该层是土星的卫星群
【答案】AD
【解析】若为土星的一部分,则它们与土星绕同一圆心做圆周运动的角速度应同土星相同,根据v=Rω可知v∝R.若为土星的卫星群,则由公式G=m可得:v=,所以v2∝,故应选A、D.
4.两颗行星相距遥远,各自有一系列卫星绕各自的行做匀速圆周运动,其卫星的线速度的平方与其轨道半径间关系的图像分别如图所示的、实线部分,由图像可知(
)
A.
可以比较两行星的质量大小
B.
不能比较两行星的密度大小
C.
不能比较两星球表面处的加速度大小
D.
在行星上将相同的卫星发射出去,需更大的发射速度
【答案】A
【解析】卫星绕行星运动,设行星质量M,卫星质量m,轨道半径r,则,,知斜率,所以,A正确;由图像知两行星半径相等,由知,B错误;在行星表面质量为物体有,可判断加速度大小,C错误;当卫星绕行星表面运行,发射速度最小,由知,所以,D错误.
5.火星探测项目我过继神舟载人航天工程、嫦娥探月工程之后又一个重大太空探索项目。假设火星探测器在火星表面附近圆形轨道运行周期为,神州飞船在地球表面附近圆形轨道运行周期为,火星质量与地球质量之比为p,火星半径与地球半径之比为q,则、之比为(
)
A.
B.
C.
D.
【答案】D
【解析】设中心天体的质量为M,半径为R,当航天器在星球表面飞行时,由
和,解得,即;又因为,所以,。
6.已知地球同步卫星离地面的高度约为地球半径的6倍。若某行星的平均密度为地球平均密度的一半,它的同步卫星距其表面的高度是其半径的2.5倍,则该行星的自转周期约为(
)
A.6小时
B.
12小时
C.
24小时
D.
36小时
【答案】B
【解析】地球的同步卫星的周期为T1=24小时,轨道半径为r1=7R1,密度ρ1。某行星的同步卫星周期为T2,轨道半径为r2=3.5R2,密度ρ2。根据牛顿第二定律和万有引力定律分别有:,,两式化简得小时。
7.位于贵州的“中国天眼”(FAST)是目前世界上口径最大的单天线射电望远镜,通过FAST可以测量地球与木星之间的距离.当FAST接收到来自木星的光线传播方向恰好与地球公转线速度方向相同时,测得地球与木星的距离是地球与太阳距离的k倍.若地球和木星绕太阳的运动均视为匀速圆周运动且轨道共面,则可知木星的公转周期为(
)
A.
年
B.
年
C.
年
D.
年
【答案】B
【解析】该题中,太阳、地球、木星的位置关系如图:
设地球的公转半径为R1,木星的公转半径为R2,测得地球与木星的距离是地球与太阳距离的k倍,则有:
,由开普勒第三定律有:,可得:,由于地球公转周期为1年,则有:T2年,故B正确,ACD错误.
8.为了对火星及其周围的空间环境进行探测,我国预计于2011年10月发射第一颗火星探测器“萤火一号”。假设探测器在离火星表面高度分别为和的圆轨道上运动时,周期分别为和。火星可视为质量分布均匀的球体,且忽略火星的自转影响,万有引力常量为G。仅利用以上数据,可以计算出(
)
A.火星的密度和火星表面的重力加速度
B.火星的质量和火星对“萤火一号”的引力
C.火星的半径和“萤火一号”的质量
D.火星表面的重力加速度和火星对“萤火一号”的引力
【答案】A
【解析】由于万有引力提供探测器做圆周运动的向心力,则有:;,可求得火星的质量和火星的半径,根据密度公式得:。在火星表面的物体有,可得火星表面的重力加速度,故选项A正确。
9.天文学家新发现了太阳系外的一颗行星。这颗行星的体积是地球的4.7倍,是地球的25倍。已知某一近地卫星绕地球运动的周期约为1.4小时,引力常量G=6.67×10-11N·m2/kg2,,由此估算该行星的平均密度为
(
)
A.1.8×103kg/m3
B.
5.6×103kg/m3
C.
1.1×104kg/m3
D.2.9×104kg/m3
【答案】D
【解析】本题考查天体运动的知识.首先根据近地卫星饶地球运动的向心力由万有引力提供,可求出地球的质量.然后根据,可得该行星的密度约为2.9×104kg/m3。
10.2019年1月3日,我国成功发射的“嫦娥四号”探测器在月球背面着陆,开启了人类探测月球的新篇章.若月球的质量是地球的、半径是地球的,“嫦娥四号”绕月球做匀速圆周运动的半径为月球半径的q倍,地球的第一宇宙速度为v1,则下列说法正确的是( )
A.“嫦娥四号”的发射速度小于v1
B.月球表面和地球表面的重力加速度大小之比为
C.月球的第一宇宙速度为
D.“嫦娥四号”绕月球运行的速度大小为
【答案】D
【解析】卫星发射后要克服地球的引力减速,故发射速度越大卫星飞的越远,第一宇宙速度是刚好能让卫星升空的最小速度,故“嫦娥四号”的发射速度一定大于第一宇宙速度;故A错误.根据星球表面的万有引力等于重力,可得,故有;故B错误.贴着星球表面转的卫星的线速度即为第一宇宙速度,而星球表面的万有引力提供向心力,,可得,则有,;故C错误.“嫦娥四号”绕月球转动由万有引力提供向心力,,可;故D正确.
11.为了探测X星球,载着登陆舱的探测飞船在以该星球中心为圆心,半径为r1的圆轨道上运动,周期为T1,总质量为m1.
随后登陆舱脱离飞船,变轨到离星球更近的半径为r2的圆轨道上运动,此时登陆舱的质量为m2,则( )
A.X星球的质量为M=
B.X星球表面的重力加速度为gx=
C.登陆舱在半径为r2轨道上做圆周运动的周期为
D.登陆舱在r1与r2轨道上运动时的速度大小之比为
【答案】AC
【解析】飞船绕星球做圆周运动,万有引力提供向心力,,那么X星球的质量为选项A对.飞船的向心加速度,而飞船并不是在星球表面,向心加速度不是重力加速度选项B错.根据开普勒第三定律,选项C对.,线速度,所以有选项D错.
12.随着我国登月计划的实施,我国宇航员登上月球已不是梦想;假如我国宇航员登上月球并在月球表面附近以初速度v0竖直向上抛出一个小球,经时间t后回到出发点。已知月球的半径为R,引力常量为G,则下列说法正确的是( )
A.
月球表面的重力加速度为
B.
月球的质量为
C.
宇航员在月球表面获得的速度就可能逃脱月球吸引
D.
宇航员在月球表面附近绕月球做匀速圆周运动的绕行周期为
【答案】A
【解析】小球在月球表面做竖直上抛运动,根据匀变速运动规律得:,,故A正确;物体在月球表面上时,由重力等于地月球的万有引力得:,解得:,故B错误;宇航员离开月球表面围绕月球做圆周运动至少应获得的速度大小即月球的第一宇宙速度大小,,此时宇航员刚好围绕月球圆周运动,但仍未逃脱月球吸引,故C错误;宇航员乘坐飞船在月球表面附近绕月球做匀速圆周运动,根据重力提供向心力得:mg月=,解得:,故D错误。
13.如图所示,曲线I是一颗绕地球做圆周运动的卫星轨道的示意图,其半径为R;曲线Ⅱ是一颗绕地球做椭圆运动的卫星轨道的示意图,O点为地球球心,AB为椭圆的长轴,两轨道和地心都在同一平面内,已知在两轨道上运动的卫星的周期相等,万有引力常量为G,地球质量为M,下列说法正确的是(
)
A.椭圆轨道的长轴长度为2R
B.卫星在I轨道的速率为,卫星在Ⅱ轨道B点的速率为,则>
C.卫星在I轨道的加速度大小为,卫星在Ⅱ轨道A点加速度大小为,则<
D.
若OA=0.5R,则卫星在B点的速率>
【答案】ABC
【解析】有开普勒第三定律可得:,因为周期相等,所以半长轴相等,圆轨道可以看成长半轴、短半轴都为椭圆,故,即椭圆轨道的长轴的长度为.故A正确.根据万有引力提供向心力可得:,故,由此可知轨道半径越大,线速度越小;设卫星以为半径做圆周运动的速度为,那么;又卫星Ⅱ在B点做向心运动,所以有,综上有.故B正确.卫星运动过程中只受到万有引力的作用,故有:,所以加速度为,又有,所以.故C正确.若,则,那么,所以.故D错误.
14.中国计划2020年左右建成覆盖全球的北斗卫星导航系统,发射北斗同步卫星的简化过程如图所示,先将北斗卫星发射至椭圆轨道I,再在A点从椭圆轨道I进入地球静止同步圆形轨道Ⅱ,关于卫星的运行,下列说法正确的是
A.
在轨道Ⅱ上运行时不受重力
B.
在轨道Ⅱ上运行时可经过北京正上方
C.
在轨道Ⅱ上运行的周期大于在轨道I上运行的周期
D.
在轨道Ⅱ上经过A点时加速度等于在轨道I上经过A点时的加速度
【答案】CD
【解析】卫星的轨道II上做匀速圆周运动,重力提供做圆周运动的向心力,卫星处于完全失重状态,A项错误;由于轨道II是地球静止同步轨道,卫星在轨道II运行时只能与赤道在同一平面内,B项错误;轨道II的半径大于轨道I的半长轴,根据开普勒第三定律知在轨道II上运行的周期长,C项正确;在轨道II上经过点时所受的万有引力等于在轨道I上经过点时的加速度等于在轨道I上经过点时的加速度,D项正确。故选CD。
15.今年我国将完成“北斗”系统全网布局,覆盖“一带一路”沿线国家,实现全球服务能力。如图所示,“北斗”系统由中圆轨道卫星(轨道1)、倾斜同步轨道卫星(轨道2)、静止同步轨道卫星(轨道3)组成。下列关于卫星的叙述中正确的是
A.为实现稳定的定位信息的传送,所有卫星必须对地球表面相对静止
B.卫星的运行速度大于第一宇宙速度
C.静止同步轨道卫星相对地面静止,所以处于平衡状态
D.卫星的向心加速度都小于地面重力加速度
【答案】D
【解析】只有静止同步轨道卫星是相对于地面静止的,选项A错误;卫星环绕速度,轨道半径越大线速度越小,除近地卫星外,运行速度均小于第一宇宙速度,选项B错误;静止同步轨道卫星绕地心运行,相对地面静止(同周期,与赤道共面,且自西向东转),有向心加速度,选项C错误;卫星的向心加速度,当时,,,,选项D正确。
16.2018年6月14日11时06分,探月工程嫦娥四号任务“鹊桥”中继星成为世界首颗成功进入地月拉格朗日L2点的Halo使命轨道的卫星,为地月信息联通搭建“天桥”。如图所示,该L2点位于地球与月球连线的延长线上,“鹊桥”位于该点,在几乎不消耗燃料的情况下与月球同步绕地球做圆周运动。已知地球、月球和“鹊桥”的质量分别为Me、Mm、m,地球和月球之间的平均距离为R,L2点离月球的距离为x,则
A.“鹊桥”的线速度大于月球的线速度
B.“鹊桥”的向心加速度小于月球的向心加速度
C.x满足
D.x满足
【答案】AC
【解析】根据题意“鹊桥”与月球运动的角速度相等,中继星绕地球转动的半径比月球绕地球的半径大,根据线速度可知
“鹊桥”中继星绕地球转动的线速度比月球绕地球转动的线速度大,故A正确;向心加速度.鹊桥”中继星统地球转动的向心加速度比月球绕地球转动的向心加速度大,故B错误:中继卫星的向心力由月球和地球引力的合力提供则有:对月球而言则有两式联立可解得:故C正确;D错误;故选AC
17.宇航员站在一星球表面上的某高处,沿水平方向抛出一小球.经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L.若抛出时初速度增大到原来的2倍,则抛出点与落地点之间的距离为L.已知两落地点在同一平面上,该星球的半径为R,万有引力常量为G.求该星球的质量M.
【答案】
【解析】设抛出点的高度为h,第一次平抛的水平射程为x,则有:x2+h2=L2①
由平抛运动规律得知,当初速增大到原来的2倍,其水平射程也增大到2x,可得:(2x)2+h2=(L)2②
由①②解得h==L。
设该星球上的重力加速度为g,由平抛运动的规律,得:h=gt2③
由万有引力定律与牛顿第二定律,得:G=mg④
式中m为小球的质量.联立以上各式,解得:M=
。
1.万有引力定律
1.在物理学发展的过程中,许多物理学家的科学研究推动了人类文明的进程.在对以下几位物理学家所作科学贡献的叙述中,正确的说法是(
)
A.英国物理学家牛顿用实验的方法测出万有引力常量G
B.第谷接受了哥白尼日心说的观点,并根据开普勒对行星运动观察记录的数据,应用严密的数学运算和椭圆轨道假说,得出了开普勒行星运动定律
C.亚里士多德认为两个从同一高度自由落下的物体,重物体与轻物体下落一样快
D.胡克认为只有在一定的条件下,弹簧的弹力才与弹簧的形变量成正比
【答案】D
【解析】牛顿在前人(如第谷、开普勒、笛卡尔等)研究的基础上,借助自己的力学成就总结出万有引力定律;1798年,即在牛顿发现万有引力定律一百多年以后,英国物理学家卡文迪许用扭秤实验证明万有引力定律是正确的,并测出万有引力恒量,选项A错误;开普勒对第谷长期天文观察的结果进行了创造性的研究与思考,开始他想用哥白尼的太阳系模型说明火星的运行轨道,但与第谷的观测结果有8分的误差,从而大胆地摒弃了天体做匀速圆周运动的观点,建立了开普勒定律,对行星的运动作出了更科学、更精确的描述,选项B错误;亚里士多德认为两个从同一高度自由落下的物体,物体越重下落越快,选项C错误;显然,选项D正确。
2.苹果落向地球,而不是地球向上碰到苹果,对此论断的正确解释是( )
A.由于地球质量比苹果质量大得多,地球对苹果的引力比苹果对地球的引力大得多造成的
B.由于地球对苹果的引力作用,而苹果对地球无引力作用造成的
C.由于苹果对地球的引力和地球对苹果的引力大小相等,但地球的质量远远大于苹果,地球不能产生明显的加速度
D.以上解释都不对
【答案】C
【解析】苹果与地球之间的吸引力是相互的,它们大小相等;在相同的力作用下,质量越大物体加速度越小,选项C正确。
3.地球可近似看成球形,由于地球表面上物体都随地球自转,所以有( )
A.物体在赤道处受的地球引力等于两极处,而重力小于两极处
B.赤道处的角速度比南纬30°大
C.地球上物体的向心加速度都指向地心,且赤道上物体的向心加速度比两极处大
D.地面上的物体随地球自转时提供向心力的是重力
【答案】A
【解析】由F=G可知,物体在地球表面任何位置受到地球的引力都相等,此引力的两个分力一个是物体的重力,另一个是物体随地球自转的向心力.在赤道上,向心力最大,重力最小,选项A正确;地表各处的角速度均等于地球自转的角速度,选项B错误;地球上只有赤道上的物体向心加速度指向地心,其他位置的向心加速度均不指向地心,选项C错误;地面上物体随地球自转的向心力是万有引力与地面支持力的合力,选项D错误.
4.牛顿以天体之间普遍存在着引力为依据,运用严密的逻辑推理,建立了万有引力定律.在创建万有引力定律的过程中,牛顿(
)
A.接受了胡克等科学家关于“吸引力与两中心距离的平方成反比”的猜想
B.根据地球上一切物体都以相同加速度下落的事实,得出物体受地球的引力与其质量成正比,即F∝m的结论
C.根据F∝m和牛顿第三定律,分析了地月间的引力关系,进而得出F∝m1m2
D.根据大量实验数据得出了比例系数G的大小
【答案】A、B.
【解析】在创建万有引力定律的过程中,牛顿接受了平方反比猜想,和物体受地球的引力与其质量成正比,即F∝m的结论,而提出万有引力定律.后来卡文迪许利用扭秤测量出万有引力常量G的大小,只有选项C是在建立万有引力定律后才进行的探索,因此符合题意的只有选项A、B.
5.地球可近似看成球形,由于地球表面上物体都随地球自转,所以有( )
A.物体在赤道处受的地球引力等于两极处,而重力小于两极处
B.赤道处的角速度比南纬30°大
C.地球上物体的向心加速度都指向地心,且赤道上物体的向心加速度比两极处大
D.地面上的物体随地球自转时提供向心力的是重力
【答案】A
【解析】由F=G可知,物体在地球表面任何位置受到地球的引力都相等,此引力的两个分力一个是物体的重力,另一个是物体随地球自转的向心力.在赤道上,向心力最大,重力最小,A对.地表各处的角速度均等于地球自转的角速度,B错.地球上只有赤道上的物体向心加速度指向地心,其他位置的向心加速度均不指向地心,C错.地面上物体随地球自转的向心力是万有引力与地面支持力的合力,D错.
6.两艘质量各为1×107kg的轮船相距100m时,它们之间的万有引力相当于( )
A.一个人的重力量级
B.一个鸡蛋的重力量级
C.一个西瓜的重力量级
D.一头牛的重力量级
【答案】B
【解析】由F引=G得F引=0.667N相当于一个鸡蛋的重力量级.
7.据报道,最近在太阳系外发现了首颗“宜居”行星,其质量约为地球质量的6.4倍,一个在地球表面重量为600N的人在这个行星表面的重量将变为960N.由此可推知,该行星的半径与地球半径之比约为( )
A.0.5
B.2
C.3.2
D.4
【答案】B
【解析】若地球质量为M0,则“宜居”行星质量为M=6.4M0,由mg=G得:=·=,所以===2.
8.1990年5月,紫金山天文台将他们发现的第2
752号小行星命名为吴健雄星,该小行星的半径为16
km.若将此小行星和地球均看成质量分布均匀的球体,小行星密度与地球相同.已知地球半径R=6
400
km,地球表面重力加速度为g.这个小行星表面的重力加速度为( )
A.400g B.g C.20g D.g
【答案】B
【解析】质量分布均匀的球体的密度ρ=3M/4πR3,地球表面的重力加速度g=GM/R2=,吴健雄星表面的重力加速度g′=GM/r2=,g/g′=R/r=400,g′=g,故选项B正确.
9.假设地球是一半径为R、质量分布均匀的球体。一矿井深度为d。已知质量分布均匀的球壳对壳内物体的引力为零。矿井底部和地面处的重力加速度大小之比为(
)
A.
B.
C.
D.
【答案】A
【解析】物体在地面上时的重力加速度可由得出。根据题中条件,球壳对其内部物体的引力为零,可认为矿井部分为一质量均匀球壳,
故矿井底部处重力加速度可由得出,故
10.位于贵州的“中国天眼”(FAST)是目前世界上口径最大的单天线射电望远镜,通过FAST可以测量地球与木星之间的距离.当FAST接收到来自木星的光线传播方向恰好与地球公转线速度方向相同时,测得地球与木星的距离是地球与太阳距离的k倍.若地球和木星绕太阳的运动均视为匀速圆周运动且轨道共面,则可知木星的公转周期为(
)
A.
年
B.
年
C.
年
D.
年
【答案】B
【解析】该题中,太阳、地球、木星的位置关系如图:
设地球的公转半径为R1,木星的公转半径为R2,测得地球与木星的距离是地球与太阳距离的k倍,则有:
,由开普勒第三定律有:,可得:,由于地球公转周期为1年,则有:T2年,故B正确,ACD错误.
11.已知质量分布均匀的球壳对壳内物体的万有引力为零.假设地球是质量分布均匀的球体.如图若在地球内挖一球形内切空腔.有一小球自切点A自由释放,则小球在球形空腔内将做
(
)
A.匀速直线运动
B.加速度越来越大的直线运动
C.匀加速直线运动
D.加速度越来越小的直线运动
【答案】C
【解析】已知质量分布均匀的球壳对壳内物体的万有引力为零,那么在地球内挖一球形内切空腔后小球A受力等于地球对A的万有引力减去空腔球体的万有引力;所以设地球密度为ρ,小球A所在处到空腔球心距离为r,小球A到地球中心距离为R,则R-r为两球心的距离,那么小球A受到的合外力
那么小球受到的加速度,所以小球向球心运动,加速度不变,即小球在球形空腔内将做匀加速直线运动,C正确,ACD错误。故选C
12.在一次测定引力常量的实验里,已知一个质量是0.50kg的球.以2.6×10-10N的力吸引另一个质量是12.8×10-3kg的球.这两个球相距4.0×10-2m,地球表面的重力加速度是9.8m/s2,地球直径是12.8×103km.根据这些数据计算引力常量.
【答案】6.5×10-11N·m2/kg2
【解析】对两球应用万有引力定律,由F=G
得:G==N·m2/kg2=6.5×10-11N·m2/kg2
13.你受太阳的引力是多大?和你受地球的引力比较一下,可得出什么样的结论?太阳的质量是1.99×1030
kg,地球到太阳的距离为1.5×1011m,设你的质量是60
kg.
【答案】见解析
【解析】地球半径为6.4×106
m,与地球到太阳的距离1.5×1011
m相比相差近10万倍,因此人距太阳的距离可以认为也是1.5×1011m.故人受太阳的引力F=G=6.67×10-11×N=0.35N
人受地球的引力F′=mg=60×9.8
N=588
N
==1
680
即地球对人的引力要比太阳对人的引力大一千六百多倍,所以平时计算时可以不考虑人受太阳的万有引力.
14.一物体在地球表面时重16N,它在以5m/s2的加速度上升的火箭中的视重为9N,则此时火箭离地球表面的距离为地球半径的多少倍?(g取10m/s2)
【答案】3R
【解析】设物体视重为9N时,所在位置第三重力加速度为g’,火箭对物体的支持力FN即等于物体的视重9N。对物体应用牛顿第二定律,有:,故,
解得。
由?可得:?,
从而火箭离地球表面的距离为:???。
15.火星质量是地球质量的0.1倍,半径是地球半径的0.5倍,火星被认为是除地球之外最可能有水(有生命)的星球.在经历了4.8亿公里星际旅行的美国火星探测器“勇气”号成功在火星表面上着陆,据介绍,“勇气”号在进入火星大气层之前的速度大约是声速的1.6倍,为了保证“勇气”号安全着陆,科学家给它配备了隔热舱、降落伞、减速火箭和气囊等.进入火星大气层后,先后在不同的时刻,探测器上的降落伞打开,气囊开始充气、减速火箭点火.当探测器在着陆前3s时,探测器的速度减为零,此时,降落伞的绳子被切断,探测器自由落下,求探测器自由下落的高度.假设地球和火星均为球体,由于火星的气压只有地球的大气压强的1%,则探测器所受阻力可忽略不计.(取地球表面的重力加速度g=10m/s2)
【答案】18m
【解析】设地球质量为M地,火星质量为M火,地球半径为R地,火星半径为R火,地球表面处的重力加速度为g地,火星表面处的重力加速度为g火,根据万有引力定律:
物体在地球表面上时有G=mg地①
同理,物体在火星表面上时有G=mg火②
由①÷②得:=()2=×22=0.4
g火=0.4×g地=4m/s2
由题意知,探测器在着陆前3s时开始做自由落体运动,设探测器自由下落的高度为h,则:
h=g火t2=×4×32m=18m.
2.万有引力定律的应用
1.第一宇宙速度是物体在地球表面附近环绕地球做匀速圆周运动的速度,则有( )
A.被发射的物体质量越大,第一宇宙速度越大
B.被发射的物体质量越小,第一宇宙速度越大
C.第一宇宙速度与被发射物体的质量无关
D.第一宇宙速度与地球的质量有关
【答案】 CD
【解析】第一宇宙速度v=
与地球质量M有关,与被发射物体的质量无关.
2.2003年8月29日,火星、地球和太阳处于三点一线,上演“火星冲日”的天象奇观.这是6万年来火星距地球最近的一次,与地球之间的距离只有5576万公里,为人类研究火星提供了最佳时机.如图所示为美国宇航局最新公布的“火星冲日”的虚拟图,则有( )
A.2003年8月29日,火星的线速度大于地球的线速度
B.2003年8月29日,火星的线速度小于地球的线速度
C.2004年8月29日,火星又回到了该位置
D.2004年8月29日,火星还没有回到该位置
【答案】BD
【解析】火星和地球均绕太阳做匀速圆周运动G=m可得:v=,所以轨道半径较大的火星线速度小,B正确;火星轨道半径大,线速度小,火星运动的周期较大,所以一年后地球回到该位置,而火星则还没有回到,D正确.
3.土星外层上有一个环,为了判断它是土星的一部分还是土星的卫星群,可以测量环中各层的线速度v与该层到土星中心的距离R之间的关系来判断( )
A.若v∝R,则该层是土星的一部分
B.若v2∝R,则该层是土星的卫星群
C.若v∝,则该层是土星的一部分
D.若v2∝,则该层是土星的卫星群
【答案】AD
【解析】若为土星的一部分,则它们与土星绕同一圆心做圆周运动的角速度应同土星相同,根据v=Rω可知v∝R.若为土星的卫星群,则由公式G=m可得:v=,所以v2∝,故应选A、D.
4.两颗行星相距遥远,各自有一系列卫星绕各自的行做匀速圆周运动,其卫星的线速度的平方与其轨道半径间关系的图像分别如图所示的、实线部分,由图像可知(
)
A.
可以比较两行星的质量大小
B.
不能比较两行星的密度大小
C.
不能比较两星球表面处的加速度大小
D.
在行星上将相同的卫星发射出去,需更大的发射速度
【答案】A
【解析】卫星绕行星运动,设行星质量M,卫星质量m,轨道半径r,则,,知斜率,所以,A正确;由图像知两行星半径相等,由知,B错误;在行星表面质量为物体有,可判断加速度大小,C错误;当卫星绕行星表面运行,发射速度最小,由知,所以,D错误.
5.火星探测项目我过继神舟载人航天工程、嫦娥探月工程之后又一个重大太空探索项目。假设火星探测器在火星表面附近圆形轨道运行周期为,神州飞船在地球表面附近圆形轨道运行周期为,火星质量与地球质量之比为p,火星半径与地球半径之比为q,则、之比为(
)
A.
B.
C.
D.
【答案】D
【解析】设中心天体的质量为M,半径为R,当航天器在星球表面飞行时,由
和,解得,即;又因为,所以,。
6.已知地球同步卫星离地面的高度约为地球半径的6倍。若某行星的平均密度为地球平均密度的一半,它的同步卫星距其表面的高度是其半径的2.5倍,则该行星的自转周期约为(
)
A.6小时
B.
12小时
C.
24小时
D.
36小时
【答案】B
【解析】地球的同步卫星的周期为T1=24小时,轨道半径为r1=7R1,密度ρ1。某行星的同步卫星周期为T2,轨道半径为r2=3.5R2,密度ρ2。根据牛顿第二定律和万有引力定律分别有:,,两式化简得小时。
7.位于贵州的“中国天眼”(FAST)是目前世界上口径最大的单天线射电望远镜,通过FAST可以测量地球与木星之间的距离.当FAST接收到来自木星的光线传播方向恰好与地球公转线速度方向相同时,测得地球与木星的距离是地球与太阳距离的k倍.若地球和木星绕太阳的运动均视为匀速圆周运动且轨道共面,则可知木星的公转周期为(
)
A.
年
B.
年
C.
年
D.
年
【答案】B
【解析】该题中,太阳、地球、木星的位置关系如图:
设地球的公转半径为R1,木星的公转半径为R2,测得地球与木星的距离是地球与太阳距离的k倍,则有:
,由开普勒第三定律有:,可得:,由于地球公转周期为1年,则有:T2年,故B正确,ACD错误.
8.为了对火星及其周围的空间环境进行探测,我国预计于2011年10月发射第一颗火星探测器“萤火一号”。假设探测器在离火星表面高度分别为和的圆轨道上运动时,周期分别为和。火星可视为质量分布均匀的球体,且忽略火星的自转影响,万有引力常量为G。仅利用以上数据,可以计算出(
)
A.火星的密度和火星表面的重力加速度
B.火星的质量和火星对“萤火一号”的引力
C.火星的半径和“萤火一号”的质量
D.火星表面的重力加速度和火星对“萤火一号”的引力
【答案】A
【解析】由于万有引力提供探测器做圆周运动的向心力,则有:;,可求得火星的质量和火星的半径,根据密度公式得:。在火星表面的物体有,可得火星表面的重力加速度,故选项A正确。
9.天文学家新发现了太阳系外的一颗行星。这颗行星的体积是地球的4.7倍,是地球的25倍。已知某一近地卫星绕地球运动的周期约为1.4小时,引力常量G=6.67×10-11N·m2/kg2,,由此估算该行星的平均密度为
(
)
A.1.8×103kg/m3
B.
5.6×103kg/m3
C.
1.1×104kg/m3
D.2.9×104kg/m3
【答案】D
【解析】本题考查天体运动的知识.首先根据近地卫星饶地球运动的向心力由万有引力提供,可求出地球的质量.然后根据,可得该行星的密度约为2.9×104kg/m3。
10.2019年1月3日,我国成功发射的“嫦娥四号”探测器在月球背面着陆,开启了人类探测月球的新篇章.若月球的质量是地球的、半径是地球的,“嫦娥四号”绕月球做匀速圆周运动的半径为月球半径的q倍,地球的第一宇宙速度为v1,则下列说法正确的是( )
A.“嫦娥四号”的发射速度小于v1
B.月球表面和地球表面的重力加速度大小之比为
C.月球的第一宇宙速度为
D.“嫦娥四号”绕月球运行的速度大小为
【答案】D
【解析】卫星发射后要克服地球的引力减速,故发射速度越大卫星飞的越远,第一宇宙速度是刚好能让卫星升空的最小速度,故“嫦娥四号”的发射速度一定大于第一宇宙速度;故A错误.根据星球表面的万有引力等于重力,可得,故有;故B错误.贴着星球表面转的卫星的线速度即为第一宇宙速度,而星球表面的万有引力提供向心力,,可得,则有,;故C错误.“嫦娥四号”绕月球转动由万有引力提供向心力,,可;故D正确.
11.为了探测X星球,载着登陆舱的探测飞船在以该星球中心为圆心,半径为r1的圆轨道上运动,周期为T1,总质量为m1.
随后登陆舱脱离飞船,变轨到离星球更近的半径为r2的圆轨道上运动,此时登陆舱的质量为m2,则( )
A.X星球的质量为M=
B.X星球表面的重力加速度为gx=
C.登陆舱在半径为r2轨道上做圆周运动的周期为
D.登陆舱在r1与r2轨道上运动时的速度大小之比为
【答案】AC
【解析】飞船绕星球做圆周运动,万有引力提供向心力,,那么X星球的质量为选项A对.飞船的向心加速度,而飞船并不是在星球表面,向心加速度不是重力加速度选项B错.根据开普勒第三定律,选项C对.,线速度,所以有选项D错.
12.随着我国登月计划的实施,我国宇航员登上月球已不是梦想;假如我国宇航员登上月球并在月球表面附近以初速度v0竖直向上抛出一个小球,经时间t后回到出发点。已知月球的半径为R,引力常量为G,则下列说法正确的是( )
A.
月球表面的重力加速度为
B.
月球的质量为
C.
宇航员在月球表面获得的速度就可能逃脱月球吸引
D.
宇航员在月球表面附近绕月球做匀速圆周运动的绕行周期为
【答案】A
【解析】小球在月球表面做竖直上抛运动,根据匀变速运动规律得:,,故A正确;物体在月球表面上时,由重力等于地月球的万有引力得:,解得:,故B错误;宇航员离开月球表面围绕月球做圆周运动至少应获得的速度大小即月球的第一宇宙速度大小,,此时宇航员刚好围绕月球圆周运动,但仍未逃脱月球吸引,故C错误;宇航员乘坐飞船在月球表面附近绕月球做匀速圆周运动,根据重力提供向心力得:mg月=,解得:,故D错误。
13.如图所示,曲线I是一颗绕地球做圆周运动的卫星轨道的示意图,其半径为R;曲线Ⅱ是一颗绕地球做椭圆运动的卫星轨道的示意图,O点为地球球心,AB为椭圆的长轴,两轨道和地心都在同一平面内,已知在两轨道上运动的卫星的周期相等,万有引力常量为G,地球质量为M,下列说法正确的是(
)
A.椭圆轨道的长轴长度为2R
B.卫星在I轨道的速率为,卫星在Ⅱ轨道B点的速率为,则>
C.卫星在I轨道的加速度大小为,卫星在Ⅱ轨道A点加速度大小为,则<
D.
若OA=0.5R,则卫星在B点的速率>
【答案】ABC
【解析】有开普勒第三定律可得:,因为周期相等,所以半长轴相等,圆轨道可以看成长半轴、短半轴都为椭圆,故,即椭圆轨道的长轴的长度为.故A正确.根据万有引力提供向心力可得:,故,由此可知轨道半径越大,线速度越小;设卫星以为半径做圆周运动的速度为,那么;又卫星Ⅱ在B点做向心运动,所以有,综上有.故B正确.卫星运动过程中只受到万有引力的作用,故有:,所以加速度为,又有,所以.故C正确.若,则,那么,所以.故D错误.
14.中国计划2020年左右建成覆盖全球的北斗卫星导航系统,发射北斗同步卫星的简化过程如图所示,先将北斗卫星发射至椭圆轨道I,再在A点从椭圆轨道I进入地球静止同步圆形轨道Ⅱ,关于卫星的运行,下列说法正确的是
A.
在轨道Ⅱ上运行时不受重力
B.
在轨道Ⅱ上运行时可经过北京正上方
C.
在轨道Ⅱ上运行的周期大于在轨道I上运行的周期
D.
在轨道Ⅱ上经过A点时加速度等于在轨道I上经过A点时的加速度
【答案】CD
【解析】卫星的轨道II上做匀速圆周运动,重力提供做圆周运动的向心力,卫星处于完全失重状态,A项错误;由于轨道II是地球静止同步轨道,卫星在轨道II运行时只能与赤道在同一平面内,B项错误;轨道II的半径大于轨道I的半长轴,根据开普勒第三定律知在轨道II上运行的周期长,C项正确;在轨道II上经过点时所受的万有引力等于在轨道I上经过点时的加速度等于在轨道I上经过点时的加速度,D项正确。故选CD。
15.今年我国将完成“北斗”系统全网布局,覆盖“一带一路”沿线国家,实现全球服务能力。如图所示,“北斗”系统由中圆轨道卫星(轨道1)、倾斜同步轨道卫星(轨道2)、静止同步轨道卫星(轨道3)组成。下列关于卫星的叙述中正确的是
A.为实现稳定的定位信息的传送,所有卫星必须对地球表面相对静止
B.卫星的运行速度大于第一宇宙速度
C.静止同步轨道卫星相对地面静止,所以处于平衡状态
D.卫星的向心加速度都小于地面重力加速度
【答案】D
【解析】只有静止同步轨道卫星是相对于地面静止的,选项A错误;卫星环绕速度,轨道半径越大线速度越小,除近地卫星外,运行速度均小于第一宇宙速度,选项B错误;静止同步轨道卫星绕地心运行,相对地面静止(同周期,与赤道共面,且自西向东转),有向心加速度,选项C错误;卫星的向心加速度,当时,,,,选项D正确。
16.2018年6月14日11时06分,探月工程嫦娥四号任务“鹊桥”中继星成为世界首颗成功进入地月拉格朗日L2点的Halo使命轨道的卫星,为地月信息联通搭建“天桥”。如图所示,该L2点位于地球与月球连线的延长线上,“鹊桥”位于该点,在几乎不消耗燃料的情况下与月球同步绕地球做圆周运动。已知地球、月球和“鹊桥”的质量分别为Me、Mm、m,地球和月球之间的平均距离为R,L2点离月球的距离为x,则
A.“鹊桥”的线速度大于月球的线速度
B.“鹊桥”的向心加速度小于月球的向心加速度
C.x满足
D.x满足
【答案】AC
【解析】根据题意“鹊桥”与月球运动的角速度相等,中继星绕地球转动的半径比月球绕地球的半径大,根据线速度可知
“鹊桥”中继星绕地球转动的线速度比月球绕地球转动的线速度大,故A正确;向心加速度.鹊桥”中继星统地球转动的向心加速度比月球绕地球转动的向心加速度大,故B错误:中继卫星的向心力由月球和地球引力的合力提供则有:对月球而言则有两式联立可解得:故C正确;D错误;故选AC
17.宇航员站在一星球表面上的某高处,沿水平方向抛出一小球.经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L.若抛出时初速度增大到原来的2倍,则抛出点与落地点之间的距离为L.已知两落地点在同一平面上,该星球的半径为R,万有引力常量为G.求该星球的质量M.
【答案】
【解析】设抛出点的高度为h,第一次平抛的水平射程为x,则有:x2+h2=L2①
由平抛运动规律得知,当初速增大到原来的2倍,其水平射程也增大到2x,可得:(2x)2+h2=(L)2②
由①②解得h==L。
设该星球上的重力加速度为g,由平抛运动的规律,得:h=gt2③
由万有引力定律与牛顿第二定律,得:G=mg④
式中m为小球的质量.联立以上各式,解得:M=
。
