人教版八年级下册 第十八章 平行四边形 18.1 平行四边形同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册 第十八章 平行四边形 18.1 平行四边形同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 146.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-18 09:12:07 | ||
图片预览

文档简介
平行四边形
同步练习
一、选择题
1、下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
2、如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是( )
A.∠3=∠4??????
B.∠A+∠ADC=180°
??
C.∠1=∠2?????
D.∠A=∠5
3、已知?ABCD的周长为32,AB=4,则BC=( )
A.4????
B.12??
C.24?
?
D.28
4、在平行四边形ABCD中,∠B=60°,那么下列各式中,不能成立的是( )
A.∠D=60°?????
B.∠A=120°??
?
C.∠C+∠D=180°?
D.∠C+∠A=180°
5、四边形ABCD中,对角线AC、
BD相交于点O,给出下列四组条件:①∠ABC
=∠ADC,AD//BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB//CD,AD=BC,其中一定能判定这个四边形是平行四边形的条件有(???
)
A.4组???
??
B.3组??????
C.2组??
?????
D.1组?
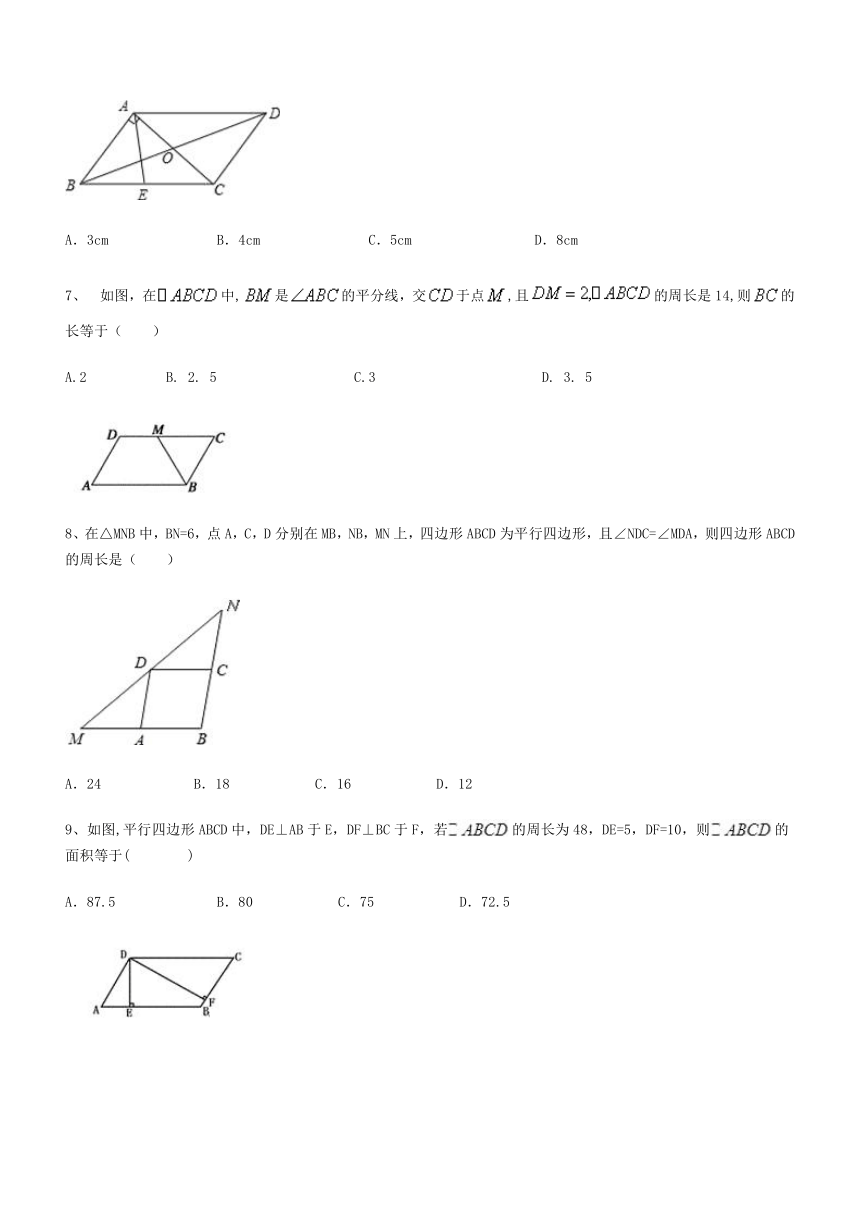
6、如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )
A.3cm???????
B.4cm???????
C.5cm????????
D.8cm
7、?如图,在中,是的平分线,交于点,且的周长是14,则的长等于( )
A.2?????
B.
2.
5?????????
C.3???????????
D.
3.
5
8、在△MNB中,BN=6,点A,C,D分别在MB,NB,MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则四边形ABCD的周长是( )
A.24??
B.18??
C.16??
D.12
9、如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若的周长为48,DE=5,DF=10,则的面积等于(????)
A.87.5
B.80
C.75
D.72.5
??
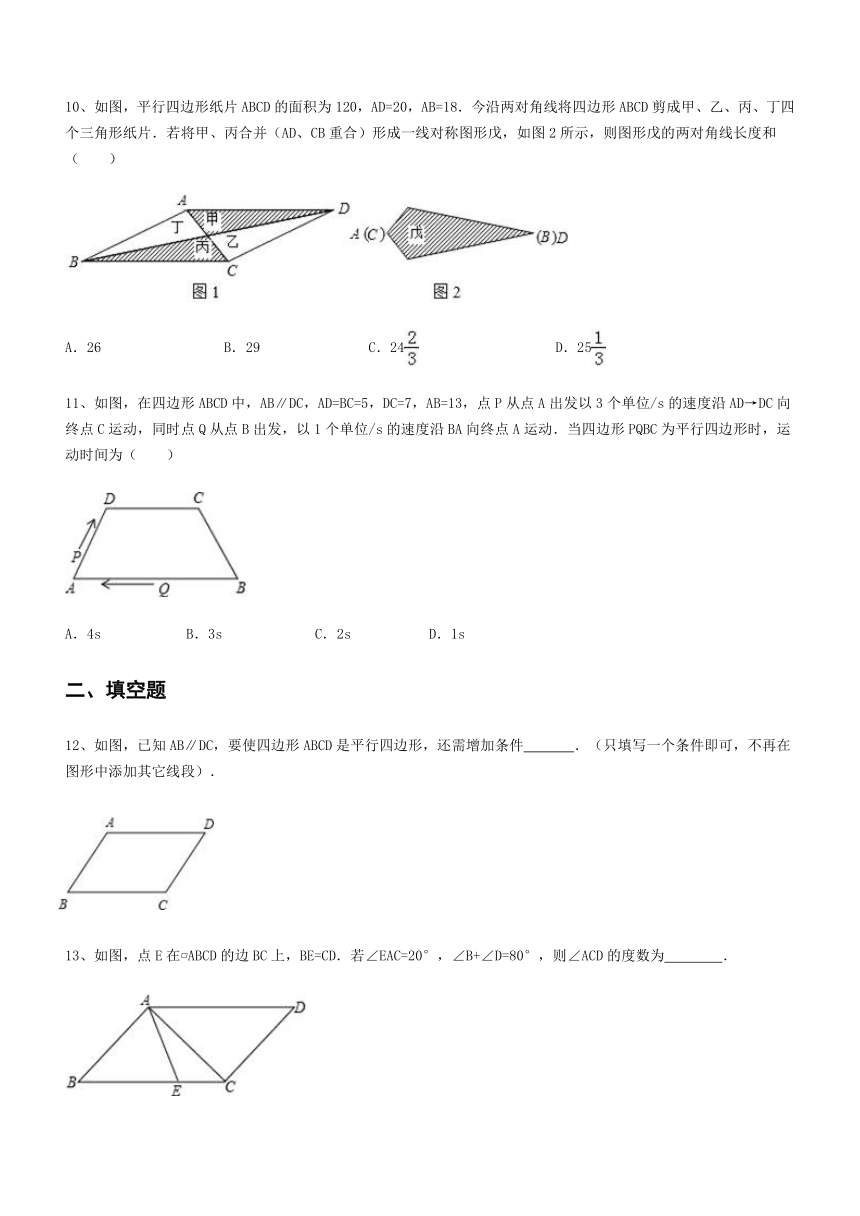
10、如图,平行四边形纸片ABCD的面积为120,AD=20,AB=18.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成一线对称图形戊,如图2所示,则图形戊的两对角线长度和( )
?
A.26????????
B.29???????
C.24????????
D.25
11、如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
A.4s
B.3s
C.2s
D.1s
二、填空题
12、如图,已知AB∥DC,要使四边形ABCD是平行四边形,还需增加条件
.(只填写一个条件即可,不再在图形中添加其它线段).
13、如图,点E在?ABCD的边BC上,BE=CD.若∠EAC=20°,∠B+∠D=80°,则∠ACD的度数为
.
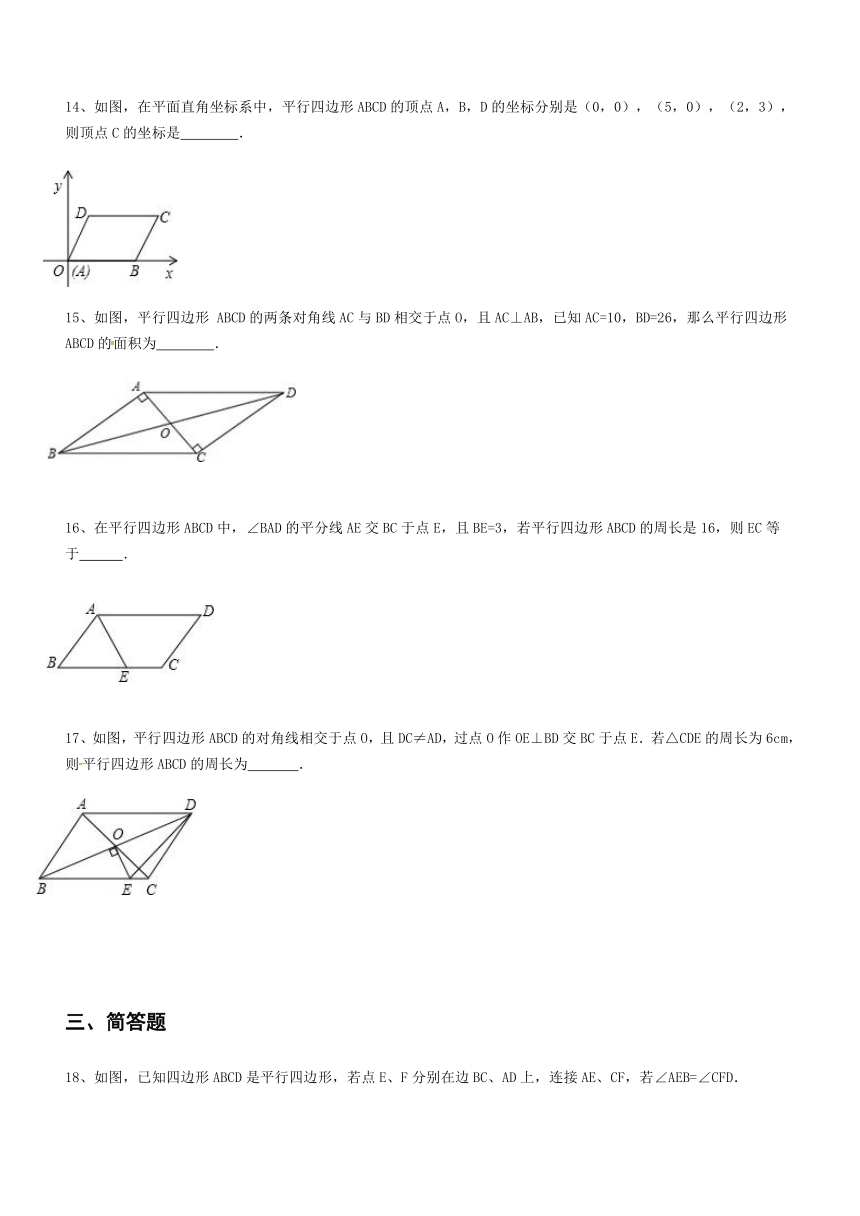
14、如图,在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是
.
15、如图,平行四边形
ABCD的两条对角线AC与BD相交于点O,且AC⊥AB,已知AC=10,BD=26,那么平行四边形ABCD的面积为
.
16、在平行四边形ABCD中,∠BAD的平分线AE交BC于点E,且BE=3,若平行四边形ABCD的周长是16,则EC等于
.
17、如图,平行四边形ABCD的对角线相交于点O,且DC≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为6cm,则平行四边形ABCD的周长为
.
三、简答题
18、如图,已知四边形ABCD是平行四边形,若点E、F分别在边BC、AD上,连接AE、CF,若∠AEB=∠CFD.
求证:四边形AECF是平行四边形.
19、如图,四边形ABCD是平行四边形,∠ABC=65°,BE平分∠ABC且交AD于E,DF∥BE,交BC于F.求∠CDF的大小.
20、如图,平行四边形ABCD的对角线相交于点O,过点O的任意一条直线与边AD相交于点E,与边BC相交于点F,求证:OE=OF.
21、如图,?ABCD中,点E、F分别在AD、BC上,且ED=BF,EF与AC相交于点O,求证:OA=OC.
22、如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在AD边上,且AE=DF,AF=CD.求证:FE=FC.
23、如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形.
参考答案
一、选择题
1、D;2、C;3、B;4、D;5、C
;6、B;7、B
;8、D;9、B;;10、A?;11、B.;
二、填空题
12、 AD∥BC??
AB=DC .(只填写一个条件即可).
13、90°
14、(7,3) .
15、120
16、2
17、12
三、简答题
18、证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠EAF,
∵∠AEB=∠CFD,
∴∠EAF=∠CFD,
∴AE∥CF,
∴四边形AECF是平行四边形.
19、解:∵四边形ABCD是平行四边形,∴DE∥BF,
∵DF∥BE,∴四边形EBFD是平行四边形,∴∠EBF=∠EDF,∴∠CDF=∠ABR,
∵∠ABC=65°,BE平分∠ABC且交AD于E,∴∠ABE=32.5°,∴∠CDF=32.5°.
20、证明::∵四边形ABCD是平行四边形,?
∴AD∥BC,OA=OC.
∴∠EAO=∠FCO,∠AEO=∠CFO,???
在△AOE和△COF中,,
∴△AEO≌△CFO(AAS),??????
∴OE=OF.
21、证明:∵四边形ABCD是平行四边形,
∴AD=CB,∠AEO=∠CFO,∠FCO=∠EAO,
又∵ED=BF,
∴AD﹣ED=BC﹣BF,即AE=CF,
在△AEO和△CFO中,,
∴△AEO≌△CFO,
∴OA=OC.
22、证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAF=∠D,
在△AEF和△FDC中,
∴△AEF≌△FDC(SAS),
∴EF=FC..
23、(1)∵△ABC和△BEF都是等边三角形,
∴AB=AC,∠EBF=∠ACB=∠BAC=60°,
∵∠EAD=60°,
∴∠EAD=∠BAC,
∴∠EAB=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD.
(2)由(1)得△ABE≌△ACD,
∴BE=CD,
∵△BEF、△ABC是等边三角形,
∴BE=EF,
∴∠EFB=∠ABC=60°,
∴EF∥CD,
∴BE=EF=CD,
∴EF=CD,且EF∥CD,
∴四边形EFCD是平行四边形.
同步练习
一、选择题
1、下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
2、如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是( )
A.∠3=∠4??????
B.∠A+∠ADC=180°
??
C.∠1=∠2?????
D.∠A=∠5
3、已知?ABCD的周长为32,AB=4,则BC=( )
A.4????
B.12??
C.24?
?
D.28
4、在平行四边形ABCD中,∠B=60°,那么下列各式中,不能成立的是( )
A.∠D=60°?????
B.∠A=120°??
?
C.∠C+∠D=180°?
D.∠C+∠A=180°
5、四边形ABCD中,对角线AC、
BD相交于点O,给出下列四组条件:①∠ABC
=∠ADC,AD//BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB//CD,AD=BC,其中一定能判定这个四边形是平行四边形的条件有(???
)
A.4组???
??
B.3组??????
C.2组??
?????
D.1组?
6、如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )
A.3cm???????
B.4cm???????
C.5cm????????
D.8cm
7、?如图,在中,是的平分线,交于点,且的周长是14,则的长等于( )
A.2?????
B.
2.
5?????????
C.3???????????
D.
3.
5
8、在△MNB中,BN=6,点A,C,D分别在MB,NB,MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则四边形ABCD的周长是( )
A.24??
B.18??
C.16??
D.12
9、如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若的周长为48,DE=5,DF=10,则的面积等于(????)
A.87.5
B.80
C.75
D.72.5
??
10、如图,平行四边形纸片ABCD的面积为120,AD=20,AB=18.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成一线对称图形戊,如图2所示,则图形戊的两对角线长度和( )
?
A.26????????
B.29???????
C.24????????
D.25
11、如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
A.4s
B.3s
C.2s
D.1s
二、填空题
12、如图,已知AB∥DC,要使四边形ABCD是平行四边形,还需增加条件
.(只填写一个条件即可,不再在图形中添加其它线段).
13、如图,点E在?ABCD的边BC上,BE=CD.若∠EAC=20°,∠B+∠D=80°,则∠ACD的度数为
.
14、如图,在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是
.
15、如图,平行四边形
ABCD的两条对角线AC与BD相交于点O,且AC⊥AB,已知AC=10,BD=26,那么平行四边形ABCD的面积为
.
16、在平行四边形ABCD中,∠BAD的平分线AE交BC于点E,且BE=3,若平行四边形ABCD的周长是16,则EC等于
.
17、如图,平行四边形ABCD的对角线相交于点O,且DC≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为6cm,则平行四边形ABCD的周长为
.
三、简答题
18、如图,已知四边形ABCD是平行四边形,若点E、F分别在边BC、AD上,连接AE、CF,若∠AEB=∠CFD.
求证:四边形AECF是平行四边形.
19、如图,四边形ABCD是平行四边形,∠ABC=65°,BE平分∠ABC且交AD于E,DF∥BE,交BC于F.求∠CDF的大小.
20、如图,平行四边形ABCD的对角线相交于点O,过点O的任意一条直线与边AD相交于点E,与边BC相交于点F,求证:OE=OF.
21、如图,?ABCD中,点E、F分别在AD、BC上,且ED=BF,EF与AC相交于点O,求证:OA=OC.
22、如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在AD边上,且AE=DF,AF=CD.求证:FE=FC.
23、如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形.
参考答案
一、选择题
1、D;2、C;3、B;4、D;5、C
;6、B;7、B
;8、D;9、B;;10、A?;11、B.;
二、填空题
12、 AD∥BC??
AB=DC .(只填写一个条件即可).
13、90°
14、(7,3) .
15、120
16、2
17、12
三、简答题
18、证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠EAF,
∵∠AEB=∠CFD,
∴∠EAF=∠CFD,
∴AE∥CF,
∴四边形AECF是平行四边形.
19、解:∵四边形ABCD是平行四边形,∴DE∥BF,
∵DF∥BE,∴四边形EBFD是平行四边形,∴∠EBF=∠EDF,∴∠CDF=∠ABR,
∵∠ABC=65°,BE平分∠ABC且交AD于E,∴∠ABE=32.5°,∴∠CDF=32.5°.
20、证明::∵四边形ABCD是平行四边形,?
∴AD∥BC,OA=OC.
∴∠EAO=∠FCO,∠AEO=∠CFO,???
在△AOE和△COF中,,
∴△AEO≌△CFO(AAS),??????
∴OE=OF.
21、证明:∵四边形ABCD是平行四边形,
∴AD=CB,∠AEO=∠CFO,∠FCO=∠EAO,
又∵ED=BF,
∴AD﹣ED=BC﹣BF,即AE=CF,
在△AEO和△CFO中,,
∴△AEO≌△CFO,
∴OA=OC.
22、证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAF=∠D,
在△AEF和△FDC中,
∴△AEF≌△FDC(SAS),
∴EF=FC..
23、(1)∵△ABC和△BEF都是等边三角形,
∴AB=AC,∠EBF=∠ACB=∠BAC=60°,
∵∠EAD=60°,
∴∠EAD=∠BAC,
∴∠EAB=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD.
(2)由(1)得△ABE≌△ACD,
∴BE=CD,
∵△BEF、△ABC是等边三角形,
∴BE=EF,
∴∠EFB=∠ABC=60°,
∴EF∥CD,
∴BE=EF=CD,
∴EF=CD,且EF∥CD,
∴四边形EFCD是平行四边形.
