人教版数学八年级上册11.1.2三角形的高、中线与角平分线 (2)课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.1.2三角形的高、中线与角平分线 (2)课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-12 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
11.1.2
三角形的高、中线与角平分线
0
知识回顾
问题探究
课堂小结
随堂检测
0
(1)三角形:由不在同一条直线上的三条线段首尾顺次相接组成的图形.
(2)构成三角形的元素:①
三个顶点;②
三条边;③
三个内角.
(3)三角形三边的数量关系:两边之和大于第三边,两边之差小于第三边.
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
回顾旧知
小学阶段是如何作出三角形的高的呢?
过三角形一个顶点向它的对边画垂线段.
探究一:
三角形的高
从
ABC的顶点A向它所对的边BC画垂线,垂足为D,所得线段AD叫做
ABC的边BC上的高.
知识回顾
问题探究
课堂小结
随堂检测
活动2
0
画出以下三角形的高
AD、BE、CF.
(1)一个三角形有几条高?
(2)三角形的高是什么线?
(3)三个图形的高有什么区别?它们在位置上有什么关系?
探究一:
三角形的高
思考:
线段
三条高
知识回顾
问题探究
课堂小结
随堂检测
活动2
0
画出以下三角形的高
AD、BE、CF.
探究一:
三角形的高
锐角三角形的高在三角形内部、直角三角形有两条高在边上、钝角三角形有两条高在外部;
三角形的三条高(或高所在的直线)都相交于一点(如上图点O),锐角三角形的三条高相交于三角形内部一点、直角三角形的三条高相交于直角顶点、钝角三角形的三条高所在的直线相交于三角形外部一点.
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
大胆猜想,探究新知识
妈妈有一块三角形蛋糕,她想平均分给小明和小亮,并且两人所得蛋糕均为三角形,你能帮妈妈出主意吗?
找到一边的中点,然后和这边所对的顶点相连,沿着这条连线切割,所得的两个三角形面积相等.
难点知识▲
探究二:
三角形的中线与角平分线
这个方法合理吗?
知识回顾
问题探究
课堂小结
随堂检测
活动2
0
难点知识▲
探究二:
三角形的中线与角平分线
反思过程,发现新概念
在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线.
(1)三角形的中线是什么线?
(2)一个三角形有几条中线?
(3)三角形的中线所分成的两个三角形面积有什么关系?
三角形的中线所分成的两个三角形的面积相等,因为等底等高的三角形面积相等.
思考:
线段
三条中线
知识回顾
问题探究
课堂小结
随堂检测
活动3
0
动手操作,大胆发现
如图,画出三角形的三条中线,并认真观察三条中线的位置关系.
三角形的三条中线都在三角形内部,并且相交于一点,这个点就是三角形的重心.
难点知识▲
探究二:
三角形的中线与角平分线
你发现了什么?
知识回顾
问题探究
课堂小结
随堂检测
活动4
0
集思广益,探究新知
请同学们画出三角形中∠A的平分线(量角器)
你能画出三角形另外的两条角平分线吗?
(1)三角形的角平分线是什么线?与角平分线有什么区别?
(2)一个三角形有几条角平分线?在位置上有什么关系?
难点知识▲
探究二:
三角形的中线与角平分线
如图,∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD叫做
ABC的角平分线.
思考:
知识回顾
问题探究
课堂小结
随堂检测
活动4
0
集思广益,探究新知
任何三角形都有三条角平分线;
任何三角形的三条角平分线都在三角形内部交于一点,我们把这个点称为三角形的内心(内切圆的圆心).
三角形的角平分线是一条线段,而角平分线是一条射线.
难点知识▲
探究二:
三角形的中线与角平分线
知识回顾
问题探究
课堂小结
随堂检测
活动5
0
合作探究,发现新知
三根木条用钉子钉成一个三角形木架,扭动它,它的形状会改变么?四根木条用钉子钉成一个四边形木架,扭动它,它的形状会改变么?
三角形具有稳定性,四边形不具有稳定性.
难点知识▲
探究二:
三角形的中线与角平分线
知识回顾
问题探究
课堂小结
随堂检测
活动5
0
如图所示,木架的形状还会改变吗?
不会.斜钉一根木条后,四边形就变成了两个三角形.因为三角形具有稳定性,所以木架形状不会改变.
三角形是具有稳定性的图形,而四边形等其他多边形不具有稳定性.把不稳定的多边形转化成若干个三角形就能使其稳定.
难点知识▲
探究二:
三角形的中线与角平分线
合作探究,发现新知
例1
(1)如图(1)所示,AD、BE、CF是
ABC的三条中线,则AB=2__________,BD=_____,AE=
_____.
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
重点、难点知识★▲
探究三:
利用三角形的高、中线及角平分线的概念解决问题
三角形的高、中线、角平分线的概念及性质
(1)
D
F
E
A
B
C
AF或BF
CD
AC
【解题过程】
(1)因为AD,BE,CF是
ABC的三条中线,
则AB=2AF=2BF,BD=CD,
AE=CE=
AC;
(2)如图(2)所示,AD、BE、CF是
ABC的三条角平分线,则∠1=_____,∠3=
______,∠ACB=2______.
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
重点、难点知识★▲
探究三:
利用三角形的高、中线及角平分线的概念解决问题
三角形的高、中线、角平分线的概念及性质
4
3
2
1
(2)
D
F
E
A
B
C
【思路点拨】已知三角形的中线,找准中点可得线段的数量关系;三角形的角平分线平分三角形的一个内角,所得的两个小角相等.
∠4
∠2
∠ABC
练习:如图,在
ABC中,AE是中线,AD是角平分线,AF是高.则BE=____=
____;∠BAD=________=
________;∠AFB=________=90°.
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
∠AFC
重点、难点知识★▲
探究三:
利用三角形的高、中线及角平分线的概念解决问题
CE
BC
∠CAD
∠BAC
【思路点拨】运用高、中线、角平分线的概念进行求解.
知识回顾
问题探究
课堂小结
随堂检测
活动2
0
三角形的中线运用
重点、难点知识★▲
探究三:
利用三角形的高、中线及角平分线的概念解决问题
例2
在
ABC中,AD是
ABC的中线,E为AB的中点,则
AED的面积与
ACD的面积的数量关系
为_______________.
【思路点拨】AD是
ABC的中线,所以AD平分
ABC的面积,同理DE也平分
ABD的面积.
【解题过程】
∵AD是
ABC的中线,∴
又∵E为AB的中点,∴
知识回顾
问题探究
课堂小结
随堂检测
活动2
0
三角形的中线运用
重点、难点知识★▲
探究三:
利用三角形的高、中线及角平分线的概念解决问题
∵D、E、F分别是BC、AD、BE的中点,∴AD是
ABC的中线,BE是
ABD的中线,AF是
ABE的中线,
又∵
=1,
∴
=2
=2,
=2
=4,
=2
=8.
【解题过程】
【思路点拨】利用三角形的中线平分三角形的面积进行求解.
练习:如图,点D、E、F分别是BC、AD、BE的中点,且
=1,求
.
知识回顾
问题探究
课堂小结
随堂检测
活动3
0
三角形的稳定性
例3
下列图形具有稳定性的是(
)
A.正方形
B.长方形
C.三角形
D.梯形
【解题过程】
具有稳定性的图形是三角形,其他多边形不具有稳定性.
C
重点、难点知识★▲
探究三:
利用三角形的高、中线及角平分线的概念解决问题
【思路点拨】
三角形具有稳定性.
知识回顾
问题探究
课堂小结
随堂检测
活动3
0
练习:下列图形不具有稳定性的是(
)
选项B里含有四边形,因为四边形不具有稳定性,故选B.
B
重点、难点知识★▲
探究三:
利用三角形的高、中线及角平分线的概念解决问题
【思路点拨】找到有四边形等不具有稳定性的图形.
【解题过程】
知识梳理
知识回顾
问题探究
课堂小结
随堂检测
0
(1)三角形的高、中线、角平分线的概念.
(2)三角形的高所在直线相交于一点;三角形的中线交于三角形内部一点,这个点叫做三角形的重心;三角形三条角平分线交于三角形内部一点,这个点叫做三角形的内心.
(3)三角形的中线把三角形分成两个面积相等的三角形.
(4)三角形具有稳定性,四边形等其他多边形不具有稳定性.
重难点突破
知识回顾
问题探究
课堂小结
随堂检测
0
(1)三角形的高、中线、角平分线都是线段.
(2)注意重心和内心分别是三角形的中线和角平分线的交点.
(3)灵活运用三角形的高、中线、角平分线的概念解决有关问题.
11.1.2
三角形的高、中线与角平分线
0
知识回顾
问题探究
课堂小结
随堂检测
0
(1)三角形:由不在同一条直线上的三条线段首尾顺次相接组成的图形.
(2)构成三角形的元素:①
三个顶点;②
三条边;③
三个内角.
(3)三角形三边的数量关系:两边之和大于第三边,两边之差小于第三边.
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
回顾旧知
小学阶段是如何作出三角形的高的呢?
过三角形一个顶点向它的对边画垂线段.
探究一:
三角形的高
从
ABC的顶点A向它所对的边BC画垂线,垂足为D,所得线段AD叫做
ABC的边BC上的高.
知识回顾
问题探究
课堂小结
随堂检测
活动2
0
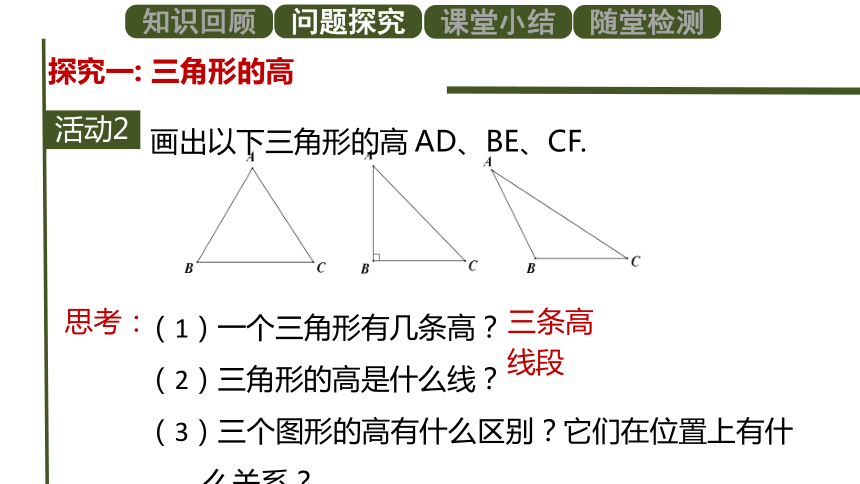
画出以下三角形的高
AD、BE、CF.
(1)一个三角形有几条高?
(2)三角形的高是什么线?
(3)三个图形的高有什么区别?它们在位置上有什么关系?
探究一:
三角形的高
思考:
线段
三条高
知识回顾
问题探究
课堂小结
随堂检测
活动2
0
画出以下三角形的高
AD、BE、CF.
探究一:
三角形的高
锐角三角形的高在三角形内部、直角三角形有两条高在边上、钝角三角形有两条高在外部;
三角形的三条高(或高所在的直线)都相交于一点(如上图点O),锐角三角形的三条高相交于三角形内部一点、直角三角形的三条高相交于直角顶点、钝角三角形的三条高所在的直线相交于三角形外部一点.
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
大胆猜想,探究新知识
妈妈有一块三角形蛋糕,她想平均分给小明和小亮,并且两人所得蛋糕均为三角形,你能帮妈妈出主意吗?
找到一边的中点,然后和这边所对的顶点相连,沿着这条连线切割,所得的两个三角形面积相等.
难点知识▲
探究二:
三角形的中线与角平分线
这个方法合理吗?
知识回顾
问题探究
课堂小结
随堂检测
活动2
0
难点知识▲
探究二:
三角形的中线与角平分线
反思过程,发现新概念
在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线.
(1)三角形的中线是什么线?
(2)一个三角形有几条中线?
(3)三角形的中线所分成的两个三角形面积有什么关系?
三角形的中线所分成的两个三角形的面积相等,因为等底等高的三角形面积相等.
思考:
线段
三条中线
知识回顾
问题探究
课堂小结
随堂检测
活动3
0
动手操作,大胆发现
如图,画出三角形的三条中线,并认真观察三条中线的位置关系.
三角形的三条中线都在三角形内部,并且相交于一点,这个点就是三角形的重心.
难点知识▲
探究二:
三角形的中线与角平分线
你发现了什么?
知识回顾
问题探究
课堂小结
随堂检测
活动4
0
集思广益,探究新知
请同学们画出三角形中∠A的平分线(量角器)
你能画出三角形另外的两条角平分线吗?
(1)三角形的角平分线是什么线?与角平分线有什么区别?
(2)一个三角形有几条角平分线?在位置上有什么关系?
难点知识▲
探究二:
三角形的中线与角平分线
如图,∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD叫做
ABC的角平分线.
思考:
知识回顾
问题探究
课堂小结
随堂检测
活动4
0
集思广益,探究新知
任何三角形都有三条角平分线;
任何三角形的三条角平分线都在三角形内部交于一点,我们把这个点称为三角形的内心(内切圆的圆心).
三角形的角平分线是一条线段,而角平分线是一条射线.
难点知识▲
探究二:
三角形的中线与角平分线
知识回顾
问题探究
课堂小结
随堂检测
活动5
0
合作探究,发现新知
三根木条用钉子钉成一个三角形木架,扭动它,它的形状会改变么?四根木条用钉子钉成一个四边形木架,扭动它,它的形状会改变么?
三角形具有稳定性,四边形不具有稳定性.
难点知识▲
探究二:
三角形的中线与角平分线
知识回顾
问题探究
课堂小结
随堂检测
活动5
0
如图所示,木架的形状还会改变吗?
不会.斜钉一根木条后,四边形就变成了两个三角形.因为三角形具有稳定性,所以木架形状不会改变.
三角形是具有稳定性的图形,而四边形等其他多边形不具有稳定性.把不稳定的多边形转化成若干个三角形就能使其稳定.
难点知识▲
探究二:
三角形的中线与角平分线
合作探究,发现新知
例1
(1)如图(1)所示,AD、BE、CF是
ABC的三条中线,则AB=2__________,BD=_____,AE=
_____.
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
重点、难点知识★▲
探究三:
利用三角形的高、中线及角平分线的概念解决问题
三角形的高、中线、角平分线的概念及性质
(1)
D
F
E
A
B
C
AF或BF
CD
AC
【解题过程】
(1)因为AD,BE,CF是
ABC的三条中线,
则AB=2AF=2BF,BD=CD,
AE=CE=
AC;
(2)如图(2)所示,AD、BE、CF是
ABC的三条角平分线,则∠1=_____,∠3=
______,∠ACB=2______.
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
重点、难点知识★▲
探究三:
利用三角形的高、中线及角平分线的概念解决问题
三角形的高、中线、角平分线的概念及性质
4
3
2
1
(2)
D
F
E
A
B
C
【思路点拨】已知三角形的中线,找准中点可得线段的数量关系;三角形的角平分线平分三角形的一个内角,所得的两个小角相等.
∠4
∠2
∠ABC
练习:如图,在
ABC中,AE是中线,AD是角平分线,AF是高.则BE=____=
____;∠BAD=________=
________;∠AFB=________=90°.
知识回顾
问题探究
课堂小结
随堂检测
活动1
0
∠AFC
重点、难点知识★▲
探究三:
利用三角形的高、中线及角平分线的概念解决问题
CE
BC
∠CAD
∠BAC
【思路点拨】运用高、中线、角平分线的概念进行求解.
知识回顾
问题探究
课堂小结
随堂检测
活动2
0
三角形的中线运用
重点、难点知识★▲
探究三:
利用三角形的高、中线及角平分线的概念解决问题
例2
在
ABC中,AD是
ABC的中线,E为AB的中点,则
AED的面积与
ACD的面积的数量关系
为_______________.
【思路点拨】AD是
ABC的中线,所以AD平分
ABC的面积,同理DE也平分
ABD的面积.
【解题过程】
∵AD是
ABC的中线,∴
又∵E为AB的中点,∴
知识回顾
问题探究
课堂小结
随堂检测
活动2
0
三角形的中线运用
重点、难点知识★▲
探究三:
利用三角形的高、中线及角平分线的概念解决问题
∵D、E、F分别是BC、AD、BE的中点,∴AD是
ABC的中线,BE是
ABD的中线,AF是
ABE的中线,
又∵
=1,
∴
=2
=2,
=2
=4,
=2
=8.
【解题过程】
【思路点拨】利用三角形的中线平分三角形的面积进行求解.
练习:如图,点D、E、F分别是BC、AD、BE的中点,且
=1,求
.
知识回顾
问题探究
课堂小结
随堂检测
活动3
0
三角形的稳定性
例3
下列图形具有稳定性的是(
)
A.正方形
B.长方形
C.三角形
D.梯形
【解题过程】
具有稳定性的图形是三角形,其他多边形不具有稳定性.
C
重点、难点知识★▲
探究三:
利用三角形的高、中线及角平分线的概念解决问题
【思路点拨】
三角形具有稳定性.
知识回顾
问题探究
课堂小结
随堂检测
活动3
0
练习:下列图形不具有稳定性的是(
)
选项B里含有四边形,因为四边形不具有稳定性,故选B.
B
重点、难点知识★▲
探究三:
利用三角形的高、中线及角平分线的概念解决问题
【思路点拨】找到有四边形等不具有稳定性的图形.
【解题过程】
知识梳理
知识回顾
问题探究
课堂小结
随堂检测
0
(1)三角形的高、中线、角平分线的概念.
(2)三角形的高所在直线相交于一点;三角形的中线交于三角形内部一点,这个点叫做三角形的重心;三角形三条角平分线交于三角形内部一点,这个点叫做三角形的内心.
(3)三角形的中线把三角形分成两个面积相等的三角形.
(4)三角形具有稳定性,四边形等其他多边形不具有稳定性.
重难点突破
知识回顾
问题探究
课堂小结
随堂检测
0
(1)三角形的高、中线、角平分线都是线段.
(2)注意重心和内心分别是三角形的中线和角平分线的交点.
(3)灵活运用三角形的高、中线、角平分线的概念解决有关问题.
