沪科版九年级数学上册第23章 解直角三角形达标测试卷 含答案
文档属性
| 名称 | 沪科版九年级数学上册第23章 解直角三角形达标测试卷 含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 336.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 17:17:19 | ||
图片预览


文档简介
第23章达标测试卷
一、选择题(每题4分,共40分)
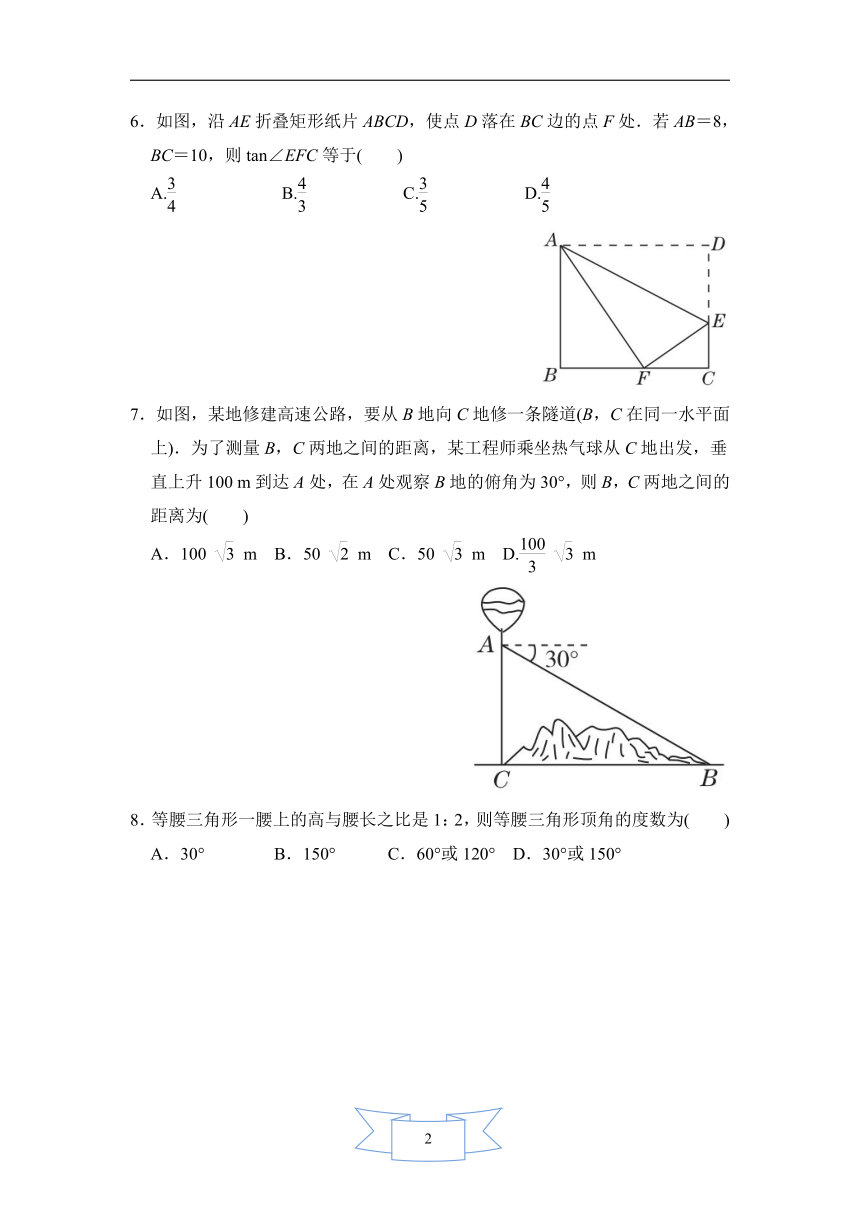
1.在Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中,正确的是( )
A.sin
B=
B.cos
B=
C.tan
B=
D.tan
B=
2.在Rt△ABC中,∠C=90°,AB=10,AC=6,则cos
A的值是( )
A.
B.
C.
D.
3.在Rt△ABC中,∠C=90°,若AB=4,sin
A=,则斜边上的高等于( )
A.
B.
C.
D.
4.如图是边长为1的小正方形组成的网格图,其中点A,B,C均为格点,则sin∠BAC为( )
A.
B.
C.
D.
5.如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠DCA=,BC=10,则AB的长是( )
A.3
B.6
C.8
D.9
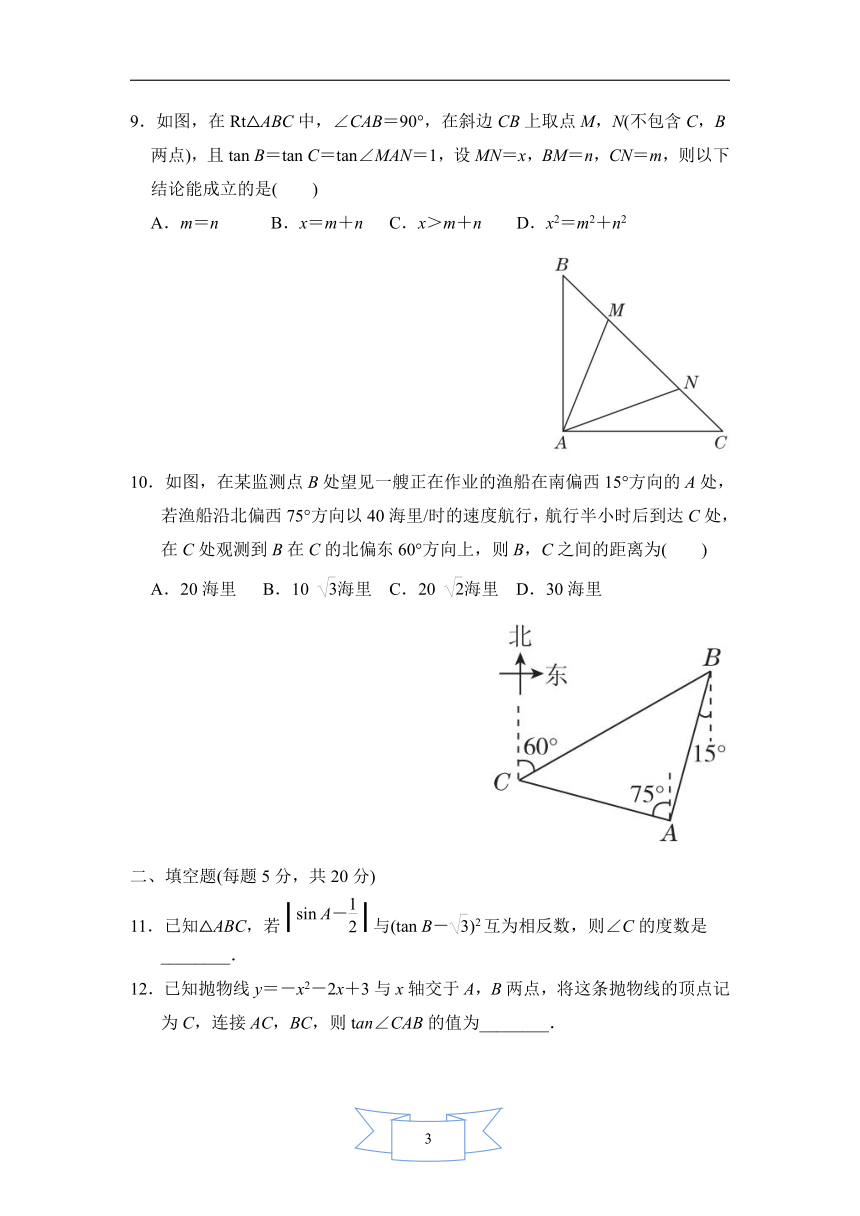
6.如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处.若AB=8,BC=10,则tan∠EFC等于( )
A.
B.
C.
D.
7.如图,某地修建高速公路,要从B地向C地修一条隧道(B,C在同一水平面上).为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100
m到达A处,在A处观察B地的俯角为30°,则B,C两地之间的距离为( )
A.100
m
B.50
m
C.50
m
D.
m
8.等腰三角形一腰上的高与腰长之比是1:2,则等腰三角形顶角的度数为( )
A.30°
B.150°
C.60°或120°
D.30°或150°
9.如图,在Rt△ABC中,∠CAB=90°,在斜边CB上取点M,N(不包含C,B两点),且tan
B=tan
C=tan∠MAN=1,设MN=x,BM=n,CN=m,则以下结论能成立的是( )
A.m=n
B.x=m+n
C.x>m+n
D.x2=m2+n2
10.如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为( )
A.20海里
B.10
海里
C.20
海里
D.30海里
二、填空题(每题5分,共20分)
11.已知△ABC,若与(tan
B-)2互为相反数,则∠C的度数是________.
12.已知抛物线y=-x2-2x+3与x轴交于A,B两点,将这条抛物线的顶点记为C,连接AC,BC,则tan∠CAB的值为________.
13.如图,正方形ABCD的边长为4,点M在边DC上,M,N两点关于对角线AC对称,若DM=1,则tan
∠ADN=________.
14.如图,已知点A(5
,0),直线y=x+b(b>0)与y轴交于点B,连接AB.若α=75°,则b=________.
三、解答题(15~18题,每题8分,19,20题,每题10分,21,22题,每题12分,23题14分,共90分)
15.计算:
(1)+(π-3)0+|1-|+tan
45°;
(2)(cos
60°)-1÷(-1)2
020+|2-|-×(tan
30°-1)0.
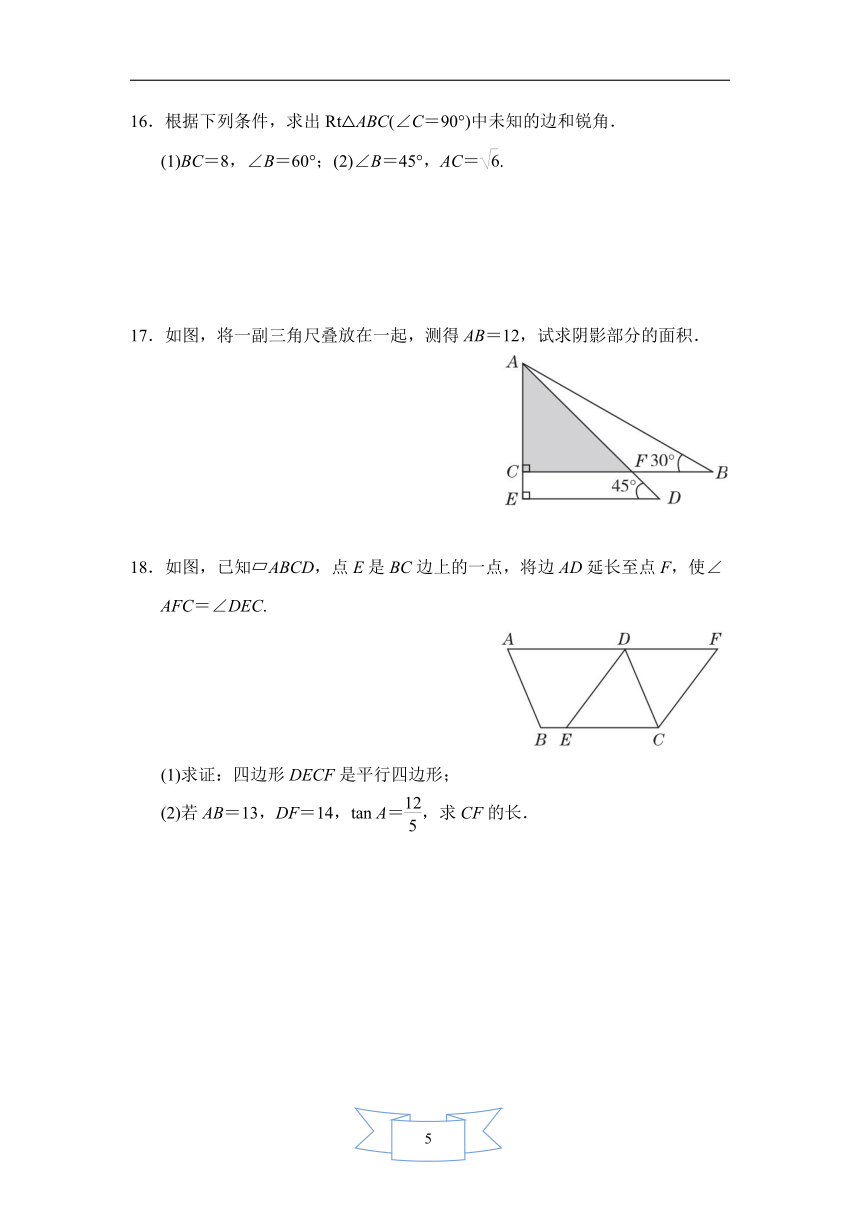
16.根据下列条件,求出Rt△ABC(∠C=90°)中未知的边和锐角.
(1)BC=8,∠B=60°;(2)∠B=45°,AC=.
17.如图,将一副三角尺叠放在一起,测得AB=12,试求阴影部分的面积.
18.如图,已知?ABCD,点E是BC边上的一点,将边AD延长至点F,使∠AFC=∠DEC.
(1)求证:四边形DECF是平行四边形;
(2)若AB=13,DF=14,tan
A=,求CF的长.
19.如图,合肥某中学九年级数学兴趣小组为测量校园主教学楼AB的高度,由于教学楼底部不能直接到达,故兴趣小组在平地上选择一点D,用测角器测得主教学楼顶端A的仰角为30°,再向主教学楼的方向前进24米,到达点E处(D,E,B三点在同一直线上),又测得主教学楼顶端A的仰角为60°,已知测角器CD的高度为1.6米,请计算主教学楼AB的高度.(≈1.73,结果精确到0.1米)
20.如图,在四边形ABCD中,∠B=∠D=90°,AB=BC,AD=7,tan
A=2.求CD的长.
21.如图,在电线杆上的C处引拉线CE,CF固定电线杆.拉线CE和地面成60°角,在离电线杆6米处安置测角仪AB,在A处测得电线杆上C处的仰角为30°.已知测角仪AB的高为1.5米,求拉线CE的长.(结果保留根号)
22.如图,在平面直角坐标系中,抛物线y=-x2+ax+b交x轴于A(1,0),B(3,0)两点,点P是抛物线上在第一象限内的一点,直线BP与y轴相交于点C.
(1)求抛物线y=-x2+ax+b的解析式;
(2)当点P是线段BC的中点时,求点P的坐标;
(3)在(2)的条件下,求sin∠OCB的值.
23.如图,有一艘渔船在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛A,B上的观测点进行观测,从A岛测得渔船在南偏东37°方向的C处,B岛在南偏东66°方向,从B岛测得渔船在正西方向,已知两个小岛间的距离为72海里.A岛上维修船的速度为20海里/时,B岛上维修船的速度为28.8海里/时,为及时赶到维修,调度中心应派遣哪个岛上的维修船前去维修?(参考数据:cos
37°≈0.8,sin
37°≈0.6,sin
66°≈0.9,cos
66°≈0.4)
答案
一、1.C
2.B 点拨:由余弦定义可得cos
A=,因为AB=10,AC=6,所以cos
A==,故选B.
3.D 4.D
5.B 点拨:因为AD=DC,所以∠DAC=∠DCA.又因为AD∥BC,所以∠DAC=∠ACB,所以∠DCA=∠ACB.在Rt△ACB中,AC=BC·cos
∠ACB=10×=8,则AB==6.
6.A 7.A
8.D 点拨:有两种情况:当顶角为锐角时,如图①,sin
A=,∠A=30°;当顶角为钝角时,如图②,sin
(180°-∠BAC)=,180°-∠BAC=30°,∠BAC=150°.
9.D 10.C
二、11.90° 点拨:由题意得sin
A=,tan
B=,因为是在△ABC中,所以∠A=30°,∠B=60°,所以∠C的度数是90°.
12.2
13. 点拨:如图,过N作NG⊥AD于点G.∵正方形ABCD的边长为4,M,N关于AC对称,DM=1,
∴MC=NC=3,∴GD=3.而GN=AB=4,∴tan
∠ADN==.
14.5 点拨:设直线y=x+b(b>0)与x轴交于点C,
易得C(-b,0),B(0,b),
∴OC=OB=b,∴∠BCO=45°.
又∵α=75°,∴∠BAO=30°.
在Rt△AOB中,∠BAO=30°,又易知OA=5
,
∴OB=OA·tan
∠BAO=5
×=5,∴b=5.
三、15.解:(1)原式=-2+1+-1+1=-1;
(2)原式=÷1+2-2-2(-1)×1=2+2-2-2+2=2.
16.解:(1)∠A=90°-∠B=90°-60°=30°.
∵sin
A=,BC=8,
∴sin
30°==,
∴AB=16,
又∵cos
A=,
∴cos
30°==,
∴AC=8
.
(2)∵∠B=45°,∠C=90°,
∴∠A=45°,
∴BC=AC=,∴AB=2
.
17.解:∵∠B=30°,∠ACB=90°,AB=12,
∴AC=6.易知BC∥ED,
∴∠AFC=∠ADE=45°,
∴AC=CF=6.
∴S△ACF=×6×6=18,
即阴影部分的面积为18.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.∴∠ADE=∠DEC.
又∵∠AFC=∠DEC,
∴∠AFC=∠ADE,∴DE∥FC.
∴四边形DECF是平行四边形.
(2)解:过点D作DH⊥BC于点H,如图.
∵四边形ABCD是平行四边形,
∴∠BCD=∠A,AB=CD=13.
又∵tan
A==tan
∠DCH=,
∴DH=12,CH=5.
∵DF=14,∴CE=14.∴EH=9.
∴DE==15.
∴CF=DE=15.
19.解:在Rt△AFG中,tan∠AFG=,
∴FG==米,
在Rt△ACG中,tan∠ACG=,
∴CG==AG米.
又∵CG-FG=24
米,
即AG-=24米,
∴AG=12米,
∴AB=12+1.6≈22.4(米).
即主教学楼AB的高度约为22.4米.
20.解:如图,延长AB,DC交于点E,
∵∠ABC=∠D=90°,
∴∠A+∠DCB=180°,
∴∠A=∠ECB,
∴tanA=tan∠ECB=2.
∵AD=7,
∴DE=AD·tan
A=14,设BC=AB=x,则BE=BC·tan
∠ECB=2x,
∴AE=3x,CE=x,在Rt△ADE中,由勾股定理得:(3x)2=72+142,解得x=
,∴CE=×
=,则CD=14-=.
21.解:如图,过点A作AM⊥CD,垂足为M.
∴AM=BD=6米,AB=MD=1.5米.
在Rt△ACM中,tan
30°=,
∴CM=AM·tan
30°=6×=2
(米).
∴CD=CM+MD=(2
+1.5)米.
在Rt△CED中,sin
60°=,
即=,
∴CE=(4+)米.
故拉线CE的长为(4+)米.
22.解:(1)将点A,B的坐标分别代入抛物线y=-x2+ax+b可得,
解得a=4,b=-3,
∴抛物线的解析式为y=-x2+4x-3;
(2)∵点C在y轴上,
∴C点的横坐标x=0,
∵点P是线段BC的中点,
∴点P的横坐标xP==,
∵点P在抛物线y=-x2+4x-3上,
∴yP=-+4×-3=,
∴点P的坐标为;
(3)∵点P的坐标为,点P是线段BC的中点,
∴点C的纵坐标为2×-0=,
∴点C的坐标为(0,),
∴BC==,
∴sin∠OCB===.
23.解:如图,作AD⊥BC,交BC的延长线于点D.
在Rt△ADB中,AD=AB·cos∠BAD=72×cos
66°≈72×0.4=28.8(海里),
BD=AB·sin
∠BAD=72×sin
66°≈72×0.9=64.8(海里).
在Rt△ADC中,AC=≈≈=36(海里).
CD=AC·sin
∠CAD≈36×sin
37°≈36×0.6=21.6(海里),
∴BC=BD-CD≈64.8-21.6=43.2(海里),
∴A岛上维修船赶到C处需要的时间
tA=≈=1.8(时),
B岛上维修船赶到C处需要的时间
tB=≈=1.5(时).
∵tA>tB,
∴调度中心应派遣B岛上的维修船前去维修.
一、选择题(每题4分,共40分)
1.在Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中,正确的是( )
A.sin
B=
B.cos
B=
C.tan
B=
D.tan
B=
2.在Rt△ABC中,∠C=90°,AB=10,AC=6,则cos
A的值是( )
A.
B.
C.
D.
3.在Rt△ABC中,∠C=90°,若AB=4,sin
A=,则斜边上的高等于( )
A.
B.
C.
D.
4.如图是边长为1的小正方形组成的网格图,其中点A,B,C均为格点,则sin∠BAC为( )
A.
B.
C.
D.
5.如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠DCA=,BC=10,则AB的长是( )
A.3
B.6
C.8
D.9
6.如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处.若AB=8,BC=10,则tan∠EFC等于( )
A.
B.
C.
D.
7.如图,某地修建高速公路,要从B地向C地修一条隧道(B,C在同一水平面上).为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100
m到达A处,在A处观察B地的俯角为30°,则B,C两地之间的距离为( )
A.100
m
B.50
m
C.50
m
D.
m
8.等腰三角形一腰上的高与腰长之比是1:2,则等腰三角形顶角的度数为( )
A.30°
B.150°
C.60°或120°
D.30°或150°
9.如图,在Rt△ABC中,∠CAB=90°,在斜边CB上取点M,N(不包含C,B两点),且tan
B=tan
C=tan∠MAN=1,设MN=x,BM=n,CN=m,则以下结论能成立的是( )
A.m=n
B.x=m+n
C.x>m+n
D.x2=m2+n2
10.如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为( )
A.20海里
B.10
海里
C.20
海里
D.30海里
二、填空题(每题5分,共20分)
11.已知△ABC,若与(tan
B-)2互为相反数,则∠C的度数是________.
12.已知抛物线y=-x2-2x+3与x轴交于A,B两点,将这条抛物线的顶点记为C,连接AC,BC,则tan∠CAB的值为________.
13.如图,正方形ABCD的边长为4,点M在边DC上,M,N两点关于对角线AC对称,若DM=1,则tan
∠ADN=________.
14.如图,已知点A(5
,0),直线y=x+b(b>0)与y轴交于点B,连接AB.若α=75°,则b=________.
三、解答题(15~18题,每题8分,19,20题,每题10分,21,22题,每题12分,23题14分,共90分)
15.计算:
(1)+(π-3)0+|1-|+tan
45°;
(2)(cos
60°)-1÷(-1)2
020+|2-|-×(tan
30°-1)0.
16.根据下列条件,求出Rt△ABC(∠C=90°)中未知的边和锐角.
(1)BC=8,∠B=60°;(2)∠B=45°,AC=.
17.如图,将一副三角尺叠放在一起,测得AB=12,试求阴影部分的面积.
18.如图,已知?ABCD,点E是BC边上的一点,将边AD延长至点F,使∠AFC=∠DEC.
(1)求证:四边形DECF是平行四边形;
(2)若AB=13,DF=14,tan
A=,求CF的长.
19.如图,合肥某中学九年级数学兴趣小组为测量校园主教学楼AB的高度,由于教学楼底部不能直接到达,故兴趣小组在平地上选择一点D,用测角器测得主教学楼顶端A的仰角为30°,再向主教学楼的方向前进24米,到达点E处(D,E,B三点在同一直线上),又测得主教学楼顶端A的仰角为60°,已知测角器CD的高度为1.6米,请计算主教学楼AB的高度.(≈1.73,结果精确到0.1米)
20.如图,在四边形ABCD中,∠B=∠D=90°,AB=BC,AD=7,tan
A=2.求CD的长.
21.如图,在电线杆上的C处引拉线CE,CF固定电线杆.拉线CE和地面成60°角,在离电线杆6米处安置测角仪AB,在A处测得电线杆上C处的仰角为30°.已知测角仪AB的高为1.5米,求拉线CE的长.(结果保留根号)
22.如图,在平面直角坐标系中,抛物线y=-x2+ax+b交x轴于A(1,0),B(3,0)两点,点P是抛物线上在第一象限内的一点,直线BP与y轴相交于点C.
(1)求抛物线y=-x2+ax+b的解析式;
(2)当点P是线段BC的中点时,求点P的坐标;
(3)在(2)的条件下,求sin∠OCB的值.
23.如图,有一艘渔船在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛A,B上的观测点进行观测,从A岛测得渔船在南偏东37°方向的C处,B岛在南偏东66°方向,从B岛测得渔船在正西方向,已知两个小岛间的距离为72海里.A岛上维修船的速度为20海里/时,B岛上维修船的速度为28.8海里/时,为及时赶到维修,调度中心应派遣哪个岛上的维修船前去维修?(参考数据:cos
37°≈0.8,sin
37°≈0.6,sin
66°≈0.9,cos
66°≈0.4)
答案
一、1.C
2.B 点拨:由余弦定义可得cos
A=,因为AB=10,AC=6,所以cos
A==,故选B.
3.D 4.D
5.B 点拨:因为AD=DC,所以∠DAC=∠DCA.又因为AD∥BC,所以∠DAC=∠ACB,所以∠DCA=∠ACB.在Rt△ACB中,AC=BC·cos
∠ACB=10×=8,则AB==6.
6.A 7.A
8.D 点拨:有两种情况:当顶角为锐角时,如图①,sin
A=,∠A=30°;当顶角为钝角时,如图②,sin
(180°-∠BAC)=,180°-∠BAC=30°,∠BAC=150°.
9.D 10.C
二、11.90° 点拨:由题意得sin
A=,tan
B=,因为是在△ABC中,所以∠A=30°,∠B=60°,所以∠C的度数是90°.
12.2
13. 点拨:如图,过N作NG⊥AD于点G.∵正方形ABCD的边长为4,M,N关于AC对称,DM=1,
∴MC=NC=3,∴GD=3.而GN=AB=4,∴tan
∠ADN==.
14.5 点拨:设直线y=x+b(b>0)与x轴交于点C,
易得C(-b,0),B(0,b),
∴OC=OB=b,∴∠BCO=45°.
又∵α=75°,∴∠BAO=30°.
在Rt△AOB中,∠BAO=30°,又易知OA=5
,
∴OB=OA·tan
∠BAO=5
×=5,∴b=5.
三、15.解:(1)原式=-2+1+-1+1=-1;
(2)原式=÷1+2-2-2(-1)×1=2+2-2-2+2=2.
16.解:(1)∠A=90°-∠B=90°-60°=30°.
∵sin
A=,BC=8,
∴sin
30°==,
∴AB=16,
又∵cos
A=,
∴cos
30°==,
∴AC=8
.
(2)∵∠B=45°,∠C=90°,
∴∠A=45°,
∴BC=AC=,∴AB=2
.
17.解:∵∠B=30°,∠ACB=90°,AB=12,
∴AC=6.易知BC∥ED,
∴∠AFC=∠ADE=45°,
∴AC=CF=6.
∴S△ACF=×6×6=18,
即阴影部分的面积为18.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.∴∠ADE=∠DEC.
又∵∠AFC=∠DEC,
∴∠AFC=∠ADE,∴DE∥FC.
∴四边形DECF是平行四边形.
(2)解:过点D作DH⊥BC于点H,如图.
∵四边形ABCD是平行四边形,
∴∠BCD=∠A,AB=CD=13.
又∵tan
A==tan
∠DCH=,
∴DH=12,CH=5.
∵DF=14,∴CE=14.∴EH=9.
∴DE==15.
∴CF=DE=15.
19.解:在Rt△AFG中,tan∠AFG=,
∴FG==米,
在Rt△ACG中,tan∠ACG=,
∴CG==AG米.
又∵CG-FG=24
米,
即AG-=24米,
∴AG=12米,
∴AB=12+1.6≈22.4(米).
即主教学楼AB的高度约为22.4米.
20.解:如图,延长AB,DC交于点E,
∵∠ABC=∠D=90°,
∴∠A+∠DCB=180°,
∴∠A=∠ECB,
∴tanA=tan∠ECB=2.
∵AD=7,
∴DE=AD·tan
A=14,设BC=AB=x,则BE=BC·tan
∠ECB=2x,
∴AE=3x,CE=x,在Rt△ADE中,由勾股定理得:(3x)2=72+142,解得x=
,∴CE=×
=,则CD=14-=.
21.解:如图,过点A作AM⊥CD,垂足为M.
∴AM=BD=6米,AB=MD=1.5米.
在Rt△ACM中,tan
30°=,
∴CM=AM·tan
30°=6×=2
(米).
∴CD=CM+MD=(2
+1.5)米.
在Rt△CED中,sin
60°=,
即=,
∴CE=(4+)米.
故拉线CE的长为(4+)米.
22.解:(1)将点A,B的坐标分别代入抛物线y=-x2+ax+b可得,
解得a=4,b=-3,
∴抛物线的解析式为y=-x2+4x-3;
(2)∵点C在y轴上,
∴C点的横坐标x=0,
∵点P是线段BC的中点,
∴点P的横坐标xP==,
∵点P在抛物线y=-x2+4x-3上,
∴yP=-+4×-3=,
∴点P的坐标为;
(3)∵点P的坐标为,点P是线段BC的中点,
∴点C的纵坐标为2×-0=,
∴点C的坐标为(0,),
∴BC==,
∴sin∠OCB===.
23.解:如图,作AD⊥BC,交BC的延长线于点D.
在Rt△ADB中,AD=AB·cos∠BAD=72×cos
66°≈72×0.4=28.8(海里),
BD=AB·sin
∠BAD=72×sin
66°≈72×0.9=64.8(海里).
在Rt△ADC中,AC=≈≈=36(海里).
CD=AC·sin
∠CAD≈36×sin
37°≈36×0.6=21.6(海里),
∴BC=BD-CD≈64.8-21.6=43.2(海里),
∴A岛上维修船赶到C处需要的时间
tA=≈=1.8(时),
B岛上维修船赶到C处需要的时间
tB=≈=1.5(时).
∵tA>tB,
∴调度中心应派遣B岛上的维修船前去维修.
