华师版九年级数学上册第24章 解直角三角形达标测试卷(含答案)
文档属性
| 名称 | 华师版九年级数学上册第24章 解直角三角形达标测试卷(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 222.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 00:00:00 | ||
图片预览


文档简介
第24章达标测试卷
一、选择题(每题3分,共30分)
1.cos
30°的值等于( )
A.
B.
C.1
D.
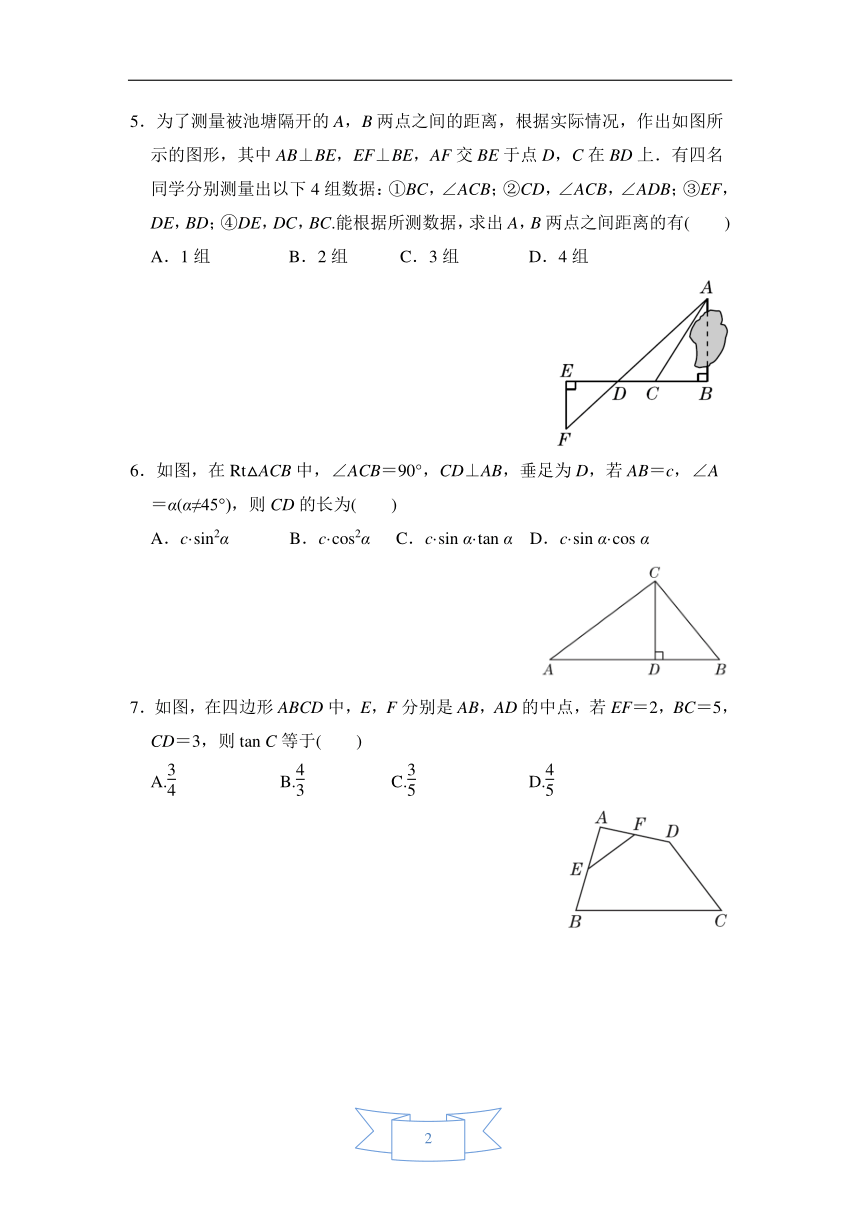
2.如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则tan
A等于( )
A.
B.
C.
D.
3.如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ACB的值为( )
A.3
B.
C.1
D.
4.如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠DCA=,BC=10,则AB的长是( )
A.3
B.6
C.8
D.9
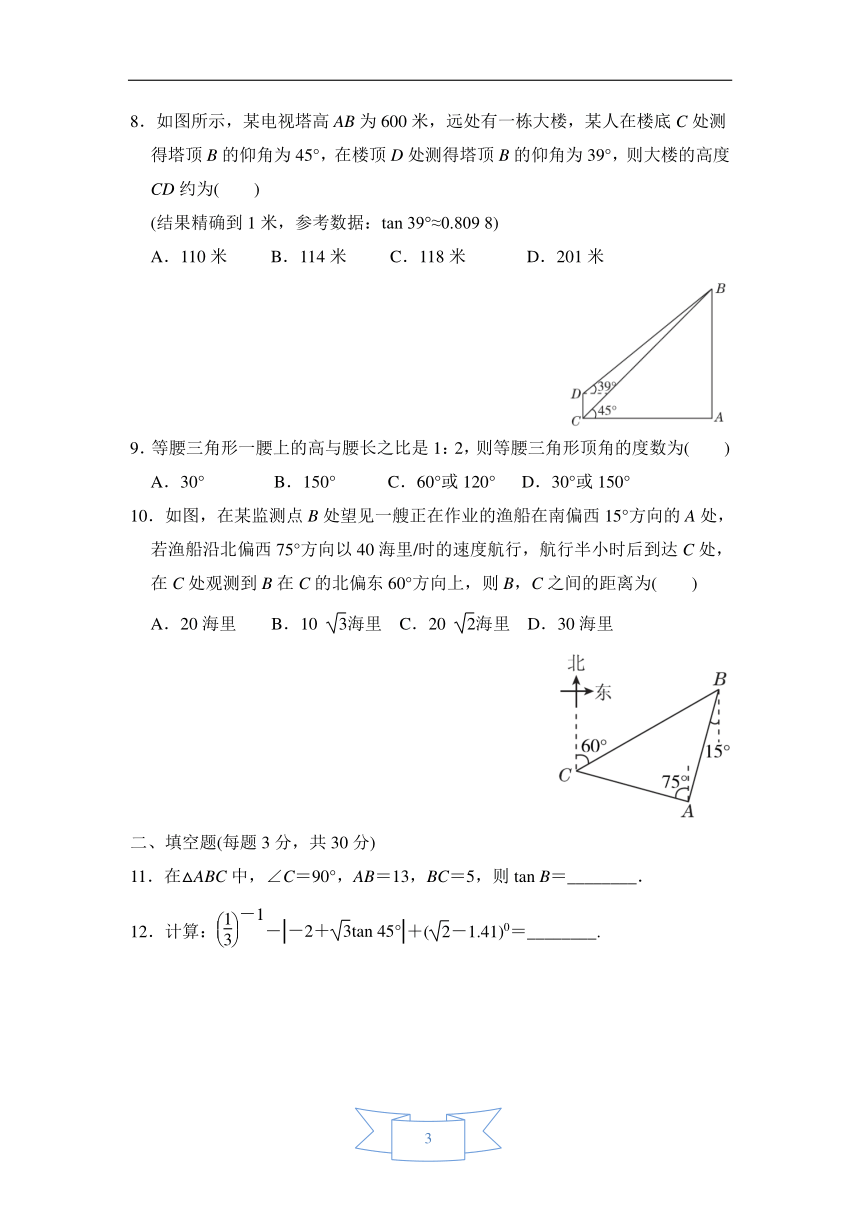
5.为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上.有四名同学分别测量出以下4组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B两点之间距离的有( )
A.1组
B.2组
C.3组
D.4组
6.如图,在Rt△ACB中,∠ACB=90°,CD⊥AB,垂足为D,若AB=c,∠A=α(α≠45°),则CD的长为( )
A.c·sin2α
B.c·cos2α
C.c·sin
α·tan
α
D.c·sin
α·cos
α
7.如图,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,则tan
C等于( )
A.
B.
C.
D.
8.如图所示,某电视塔高AB为600米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,则大楼的高度CD约为( )
(结果精确到1米,参考数据:tan
39°≈0.809
8)
A.110米
B.114米
C.118米
D.201米
9.等腰三角形一腰上的高与腰长之比是1:2,则等腰三角形顶角的度数为( )
A.30°
B.150°
C.60°或120°
D.30°或150°
10.如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为( )
A.20海里
B.10
海里
C.20
海里
D.30海里
二、填空题(每题3分,共30分)
11.在△ABC中,∠C=90°,AB=13,BC=5,则tan
B=________.
12.计算:-+(-1.41)0=________.
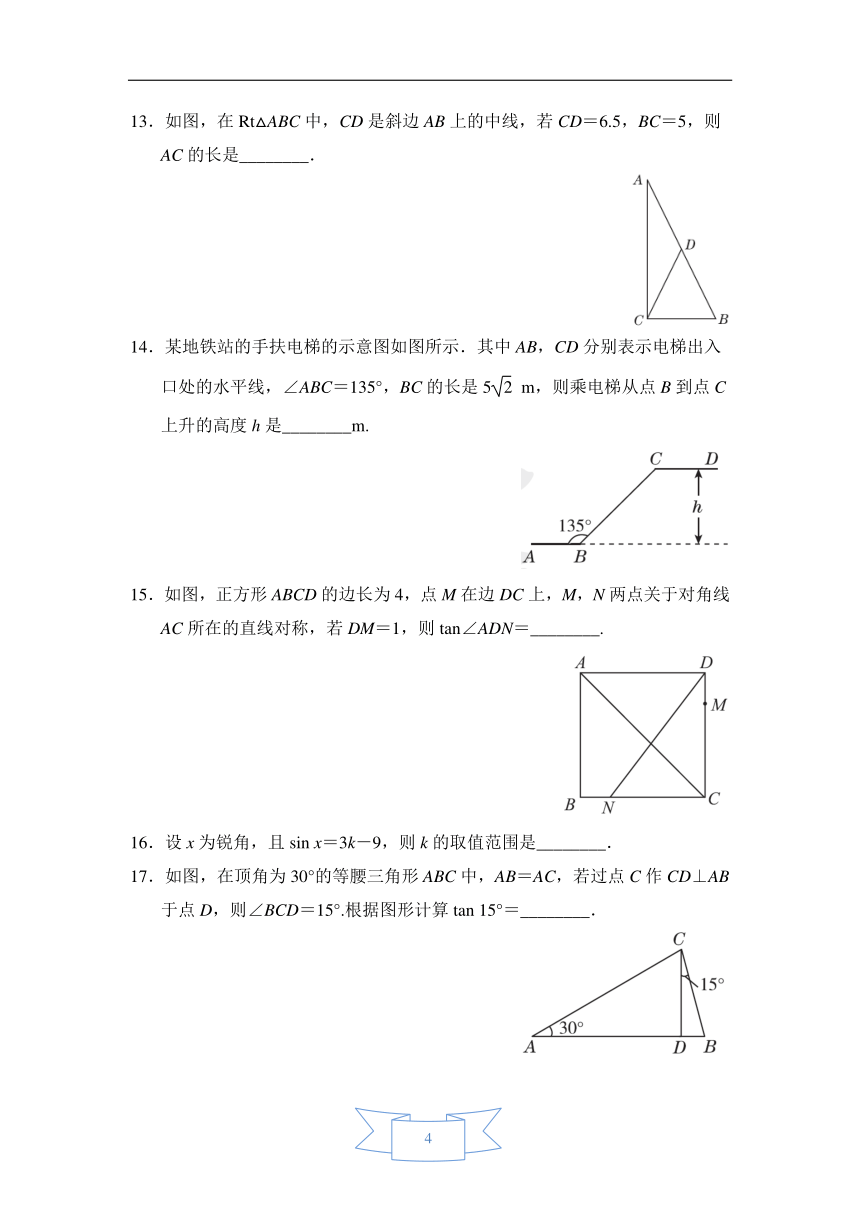
13.如图,在Rt△ABC中,CD是斜边AB上的中线,若CD=6.5,BC=5,则AC的长是________.
14.某地铁站的手扶电梯的示意图如图所示.其中AB,CD分别表示电梯出入口处的水平线,∠ABC=135°,BC的长是5
m,则乘电梯从点B到点C上升的高度h是________m.
15.如图,正方形ABCD的边长为4,点M在边DC上,M,N两点关于对角线AC所在的直线对称,若DM=1,则tan∠ADN=________.
16.设x为锐角,且sin
x=3k-9,则k的取值范围是________.
17.如图,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°.根据图形计算tan
15°=________.
18.如图,将以A为直角顶点的等腰直角三角形ABC沿直线BC平移得到△A′B′C′,使点B′与C重合,连结A′B,则tan∠A′BC′=________.
19.如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么tan∠BAD′=________.
20.一次函数的图象经过点(tan
45°,tan
60°)和(-cos
60°,-6tan
30°),则此一次函数的表达式为________.
三、解答题(21题6分,22,25题每题8分,23,24题每题12分,26题14分,共60分)
21.计算:
(1)(2cos
45°-sin
60°)+;
(2)sin
60°·cos
60°-tan
30°·tan
60°+sin245°+cos245°.
22.在△ABC中,(sin
A-1)2+=0.
(1)试判断△ABC的形状,并说明理由;
(2)若AB=10,求BC的值.
23.如图,已知△ABC中,AB=BC=5,tan∠ABC=.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
24.已知:如图,在△ABC中,AD⊥BC,D点为垂足,BE⊥AC,E点为垂足,M点为AB边的中点,连结ME,MD,ED.求证:
(1)△MED与△BMD都是等腰三角形;
(2)∠EMD=2∠DAC.
25.春汛来临之前,某防洪指挥部对长江防线的情况进行排查.发现长江边一处长500
m、高10
m、背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD,如图)急需加固,经调查论证,防洪指挥部专家组制订的加固方案是:沿背水坡面用土石进行加固,并使上底加宽3
m,加固后背水坡EF的坡比i=1:.求加固后坝底增加的宽度AF.(结果保留根号)
26.图①为学校运动会终点计时台的侧面示意图,AB∥CD,AB=1
m,DE=5
m,BC⊥DC于点C,∠ADC=30°,∠BEC=60°.
(1)求AD的长;
(2)如图②,为了避免计时台AB和AD的位置受到与水平面成45°角的光线的照射,计时台上方应放置直径是多少米的遮阳伞(即求DG的长度)?
答案
一、1.B 2.C 3.A
4.B 点拨:因为AD=DC,所以∠DAC=∠DCA.又因为AD∥BC,所以∠DAC=∠ACB.所以∠DCA=∠ACB.在Rt△ACB中,AC=BC·cos
∠BCA=10×=8,则AB==6.
5.C 点拨:对于①,可由AB=BC·tan
∠ACB求出A,B两点间的距离;对于②,由BC=,BD=,BD-BC=CD,可求出AB的长;对于③,易知△DEF∽△DBA,则=,可求出AB的长;对于④,无法求得AB的长,故有①②③共3组,故选C.
6.D
7.B 点拨:如图,连结BD,由三角形中位线定理得BD=2EF=2×2=4.又BC=5,CD=3,∴CD2+BD2=BC2.∴△BDC是直角三角形,且∠BDC=90°.∴tan
C==.
8.B
9.D 点拨:有两种情况:当顶角为锐角时,如图①,sin
A=,∴∠A=30°;当顶角为钝角时,如图②,
sin
(180°-∠BAC)=,∴180°-∠BAC=30°.∴∠BAC=150°.
10.C
二、11. 12.2+ 13.12 14.5
15.
16.3x=3k-9,所以0<3k-9<1,解得317.2-
18. 点拨:如图,过A′作A′D⊥BC′于点D,设A′D=x,则B′D=x,BC=2x,BD=3x.所以tan∠A′BC′===.
19. 点拨:由题意知BD′=BD=2
.
在Rt△ABD′中,tan
∠BAD′===.
20.y=2
x- 点拨:tan
45°=1,tan
60°=,-cos
60°=-,-6tan
30°=-2
.设y=kx+b的图象经过点(1,),,则用待定系数法可求出k=2
,b=-.
三、21.解:(1)原式=×+=2-+=2.
(2)原式=×-×++=-1++=.
22.解:(1)△ABC是等腰直角三角形.
理由:∵(sin
A-1)2+=0,
∴
∴
∴∠A=∠B=45°,
∴AC=BC,∠C=90°,
∴△ABC是等腰直角三角形.
(2)∵在△ABC中,∠C=90°,
∴sin
A==,
∴BC=10sin
45°=10×=5.
23.解:(1)过A作AE⊥BC于点E,如图,
在Rt△ABE中,tan∠ABC==,AB=5,
∴易知AE=3,BE=4,
∴CE=BC-BE=5-4=1.
在Rt△AEC中,根据勾股定理得
AC==.
(2)作BC的垂直平分线DF,交AB于点D,交BC于点F,连结CD,如图,
∵DF垂直平分BC,
∴BD=CD,BF=CF=.
∵tan∠DBF==,
∴DF=.
在Rt△BFD中,根据勾股定理得
BD==,
∴AD=5-=,
则=.
24.证明:(1)∵M为AB边的中点,AD⊥BC,BE⊥AC,
∴ME=AB,MD=AB.
∴ME=MD,
∴△MED为等腰三角形.
∵M为AB边的中点,AD⊥BC,
∴MD=BM=AB,
∴△BMD是等腰三角形.
(2)由(1)知ME=AB=MA,
∴∠MAE=∠MEA,
∴∠BME=∠MAE+∠MEA=2∠MAE.
同理可得MD=AB=MA,
∴∠MAD=∠MDA,
∴∠BMD=∠MAD+∠MDA=2∠MAD,
∴∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC.
25.解:分别过点E,D作EG⊥AB,DH⊥AB,垂足分别为点G,H.
由题意可知,EG=DH=10
m,
GH=ED=3
m.
在Rt△ADH中,
AH===10(m).
在Rt△FGE中,i==,
所以FG=EG=10
m,
所以AF=FG+GH-AH=10+3-10=(10-7)(m),
故加固后坝底增加的宽度AF为(10-7)m.
26.解:(1)过点B作BF∥AD,交DC于点F,
∴∠BFE=∠D=30°.
∵AB∥DF,
∴四边形ABFD为平行四边形,
∴DF=AB=1
m,AD=BF,
∴EF=DE-DF=4
m.
在Rt△BCF中,设BC=x
m,则BF=2x
m,CF=x
m.
在Rt△BCE中,∠BEC=60°,
∴CE=m,
∴x-=4,
解得x=2,
∴BC=2
m,
∴AD=BF=4
m.
(2)由题意知,∠BGE=45°.
在Rt△BCG中,CG=BC=2
m,
∵EC=×2=2(m),
∴GE=GC-EC=(2-2)m,
∴DG=DE-GE=(7-2)m,
即应放置直径是(7-2)m的遮阳伞.
一、选择题(每题3分,共30分)
1.cos
30°的值等于( )
A.
B.
C.1
D.
2.如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则tan
A等于( )
A.
B.
C.
D.
3.如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ACB的值为( )
A.3
B.
C.1
D.
4.如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠DCA=,BC=10,则AB的长是( )
A.3
B.6
C.8
D.9
5.为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上.有四名同学分别测量出以下4组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B两点之间距离的有( )
A.1组
B.2组
C.3组
D.4组
6.如图,在Rt△ACB中,∠ACB=90°,CD⊥AB,垂足为D,若AB=c,∠A=α(α≠45°),则CD的长为( )
A.c·sin2α
B.c·cos2α
C.c·sin
α·tan
α
D.c·sin
α·cos
α
7.如图,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,则tan
C等于( )
A.
B.
C.
D.
8.如图所示,某电视塔高AB为600米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,则大楼的高度CD约为( )
(结果精确到1米,参考数据:tan
39°≈0.809
8)
A.110米
B.114米
C.118米
D.201米
9.等腰三角形一腰上的高与腰长之比是1:2,则等腰三角形顶角的度数为( )
A.30°
B.150°
C.60°或120°
D.30°或150°
10.如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为( )
A.20海里
B.10
海里
C.20
海里
D.30海里
二、填空题(每题3分,共30分)
11.在△ABC中,∠C=90°,AB=13,BC=5,则tan
B=________.
12.计算:-+(-1.41)0=________.
13.如图,在Rt△ABC中,CD是斜边AB上的中线,若CD=6.5,BC=5,则AC的长是________.
14.某地铁站的手扶电梯的示意图如图所示.其中AB,CD分别表示电梯出入口处的水平线,∠ABC=135°,BC的长是5
m,则乘电梯从点B到点C上升的高度h是________m.
15.如图,正方形ABCD的边长为4,点M在边DC上,M,N两点关于对角线AC所在的直线对称,若DM=1,则tan∠ADN=________.
16.设x为锐角,且sin
x=3k-9,则k的取值范围是________.
17.如图,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°.根据图形计算tan
15°=________.
18.如图,将以A为直角顶点的等腰直角三角形ABC沿直线BC平移得到△A′B′C′,使点B′与C重合,连结A′B,则tan∠A′BC′=________.
19.如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么tan∠BAD′=________.
20.一次函数的图象经过点(tan
45°,tan
60°)和(-cos
60°,-6tan
30°),则此一次函数的表达式为________.
三、解答题(21题6分,22,25题每题8分,23,24题每题12分,26题14分,共60分)
21.计算:
(1)(2cos
45°-sin
60°)+;
(2)sin
60°·cos
60°-tan
30°·tan
60°+sin245°+cos245°.
22.在△ABC中,(sin
A-1)2+=0.
(1)试判断△ABC的形状,并说明理由;
(2)若AB=10,求BC的值.
23.如图,已知△ABC中,AB=BC=5,tan∠ABC=.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
24.已知:如图,在△ABC中,AD⊥BC,D点为垂足,BE⊥AC,E点为垂足,M点为AB边的中点,连结ME,MD,ED.求证:
(1)△MED与△BMD都是等腰三角形;
(2)∠EMD=2∠DAC.
25.春汛来临之前,某防洪指挥部对长江防线的情况进行排查.发现长江边一处长500
m、高10
m、背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD,如图)急需加固,经调查论证,防洪指挥部专家组制订的加固方案是:沿背水坡面用土石进行加固,并使上底加宽3
m,加固后背水坡EF的坡比i=1:.求加固后坝底增加的宽度AF.(结果保留根号)
26.图①为学校运动会终点计时台的侧面示意图,AB∥CD,AB=1
m,DE=5
m,BC⊥DC于点C,∠ADC=30°,∠BEC=60°.
(1)求AD的长;
(2)如图②,为了避免计时台AB和AD的位置受到与水平面成45°角的光线的照射,计时台上方应放置直径是多少米的遮阳伞(即求DG的长度)?
答案
一、1.B 2.C 3.A
4.B 点拨:因为AD=DC,所以∠DAC=∠DCA.又因为AD∥BC,所以∠DAC=∠ACB.所以∠DCA=∠ACB.在Rt△ACB中,AC=BC·cos
∠BCA=10×=8,则AB==6.
5.C 点拨:对于①,可由AB=BC·tan
∠ACB求出A,B两点间的距离;对于②,由BC=,BD=,BD-BC=CD,可求出AB的长;对于③,易知△DEF∽△DBA,则=,可求出AB的长;对于④,无法求得AB的长,故有①②③共3组,故选C.
6.D
7.B 点拨:如图,连结BD,由三角形中位线定理得BD=2EF=2×2=4.又BC=5,CD=3,∴CD2+BD2=BC2.∴△BDC是直角三角形,且∠BDC=90°.∴tan
C==.
8.B
9.D 点拨:有两种情况:当顶角为锐角时,如图①,sin
A=,∴∠A=30°;当顶角为钝角时,如图②,
sin
(180°-∠BAC)=,∴180°-∠BAC=30°.∴∠BAC=150°.
10.C
二、11. 12.2+ 13.12 14.5
15.
16.3
18. 点拨:如图,过A′作A′D⊥BC′于点D,设A′D=x,则B′D=x,BC=2x,BD=3x.所以tan∠A′BC′===.
19. 点拨:由题意知BD′=BD=2
.
在Rt△ABD′中,tan
∠BAD′===.
20.y=2
x- 点拨:tan
45°=1,tan
60°=,-cos
60°=-,-6tan
30°=-2
.设y=kx+b的图象经过点(1,),,则用待定系数法可求出k=2
,b=-.
三、21.解:(1)原式=×+=2-+=2.
(2)原式=×-×++=-1++=.
22.解:(1)△ABC是等腰直角三角形.
理由:∵(sin
A-1)2+=0,
∴
∴
∴∠A=∠B=45°,
∴AC=BC,∠C=90°,
∴△ABC是等腰直角三角形.
(2)∵在△ABC中,∠C=90°,
∴sin
A==,
∴BC=10sin
45°=10×=5.
23.解:(1)过A作AE⊥BC于点E,如图,
在Rt△ABE中,tan∠ABC==,AB=5,
∴易知AE=3,BE=4,
∴CE=BC-BE=5-4=1.
在Rt△AEC中,根据勾股定理得
AC==.
(2)作BC的垂直平分线DF,交AB于点D,交BC于点F,连结CD,如图,
∵DF垂直平分BC,
∴BD=CD,BF=CF=.
∵tan∠DBF==,
∴DF=.
在Rt△BFD中,根据勾股定理得
BD==,
∴AD=5-=,
则=.
24.证明:(1)∵M为AB边的中点,AD⊥BC,BE⊥AC,
∴ME=AB,MD=AB.
∴ME=MD,
∴△MED为等腰三角形.
∵M为AB边的中点,AD⊥BC,
∴MD=BM=AB,
∴△BMD是等腰三角形.
(2)由(1)知ME=AB=MA,
∴∠MAE=∠MEA,
∴∠BME=∠MAE+∠MEA=2∠MAE.
同理可得MD=AB=MA,
∴∠MAD=∠MDA,
∴∠BMD=∠MAD+∠MDA=2∠MAD,
∴∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC.
25.解:分别过点E,D作EG⊥AB,DH⊥AB,垂足分别为点G,H.
由题意可知,EG=DH=10
m,
GH=ED=3
m.
在Rt△ADH中,
AH===10(m).
在Rt△FGE中,i==,
所以FG=EG=10
m,
所以AF=FG+GH-AH=10+3-10=(10-7)(m),
故加固后坝底增加的宽度AF为(10-7)m.
26.解:(1)过点B作BF∥AD,交DC于点F,
∴∠BFE=∠D=30°.
∵AB∥DF,
∴四边形ABFD为平行四边形,
∴DF=AB=1
m,AD=BF,
∴EF=DE-DF=4
m.
在Rt△BCF中,设BC=x
m,则BF=2x
m,CF=x
m.
在Rt△BCE中,∠BEC=60°,
∴CE=m,
∴x-=4,
解得x=2,
∴BC=2
m,
∴AD=BF=4
m.
(2)由题意知,∠BGE=45°.
在Rt△BCG中,CG=BC=2
m,
∵EC=×2=2(m),
∴GE=GC-EC=(2-2)m,
∴DG=DE-GE=(7-2)m,
即应放置直径是(7-2)m的遮阳伞.
