鲁教版(五四制)数学九年级上册第一章 反比例函数达标测试卷(含答案)
文档属性
| 名称 | 鲁教版(五四制)数学九年级上册第一章 反比例函数达标测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 286.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 18:10:55 | ||
图片预览



文档简介
第一章达标测试卷
一、选择题(每题3分,共30分)
1.下列函数中,表示y是x的反比例函数的是( )
A.x(y+1)=1 B.y= C.y=- D.y=
2.反比例函数y=的图象经过点(3,-2),下列各点在图象上的是( )
A.(-3,-2)
B.(3,2)
C.(-2,-3)
D.(-2,3)
3.已知反比例函数y=,下列结论中不正确的是( )
A.其图象经过点(3,1)
B.其图象分别位于第一、第三象限
C.当x>0时,y随x的增大而减小
D.当x>1时,y>3
4.为了更好保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足关系式V=Sh(V≠0),则S关于h的函数图象大致是( )
5.若在同一直角坐标系中,正比例函数y=k1x与反比例函数y=的图象无交点,则有( )
A.k1+k2>0
B.k1+k2<0
C.k1k2>0
D.k1k2<0
6.已知点A(-1,y1),B(2,y2)都在双曲线y=上,且y1>y2,则m的取值范围是( )
A.m<0
B.m>0
C.m>-3
D.m<-3
7.y=ax+b与y=,其中ab<0,a,b为常数,它们在同一坐标系中的图象可以是( )
8.如图所示,直线y=x+2与双曲线y=相交于点A,点A的纵坐标为3,则k的值为( )
A.1
B.2
C.3
D.4
9.如图,A,B两点在反比例函数y=的图象上,C,D两点在反比例函数y=的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=,则k2-k1的值为( )
A.4
B.
C.
D.6
10.反比例函数y=(a>0,a为常数)和y=在第一象限内的图象如图所示,点M在y=的图象上,MC⊥x轴于点C,交y=的图象于点A;MD⊥y轴于点D,交y=的图象于点B.当点M在y=(x>0)的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,点B是MD的中点.其中正确的结论有( )
A.0个
B.1个
C.2个
D.3个
二、填空题(每题3分,共24分)
11.一个反比例函数的图象过点A(-2,-3),则这个反比例函数的表达式是________.
12.若点(2,y1),(3,y2)在函数y=-的图象上,则y1________y2(填“>”“<”或“=”).
13.已知直线y=ax(a≠0)与反比例函数y=(k≠0)的图象一个交点的坐标为(2,4),则它们另一个交点的坐标是________.
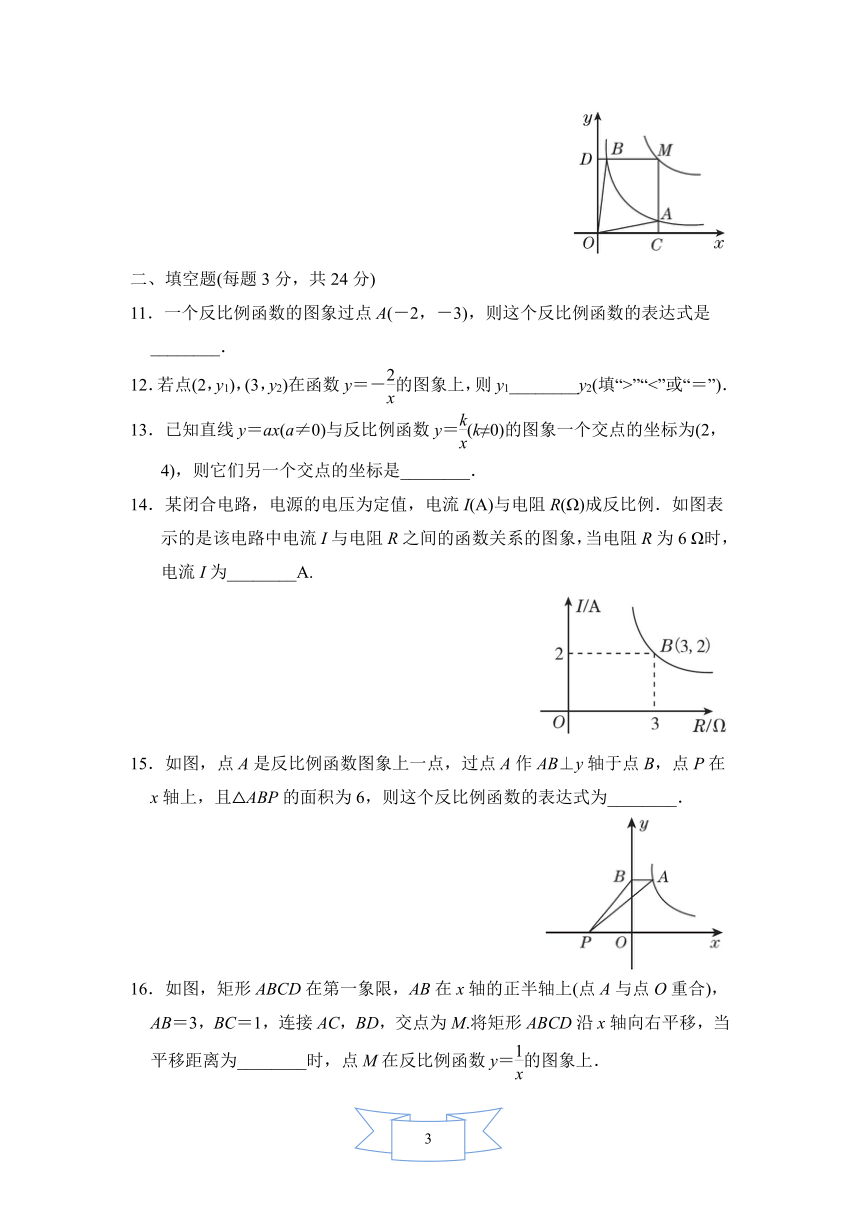
14.某闭合电路,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图表示的是该电路中电流I与电阻R之间的函数关系的图象,当电阻R为6
Ω时,电流I为________A.
15.如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,且△ABP的面积为6,则这个反比例函数的表达式为________.
16.如图,矩形ABCD在第一象限,AB在x轴的正半轴上(点A与点O重合),AB=3,BC=1,连接AC,BD,交点为M.将矩形ABCD沿x轴向右平移,当平移距离为________时,点M在反比例函数y=的图象上.
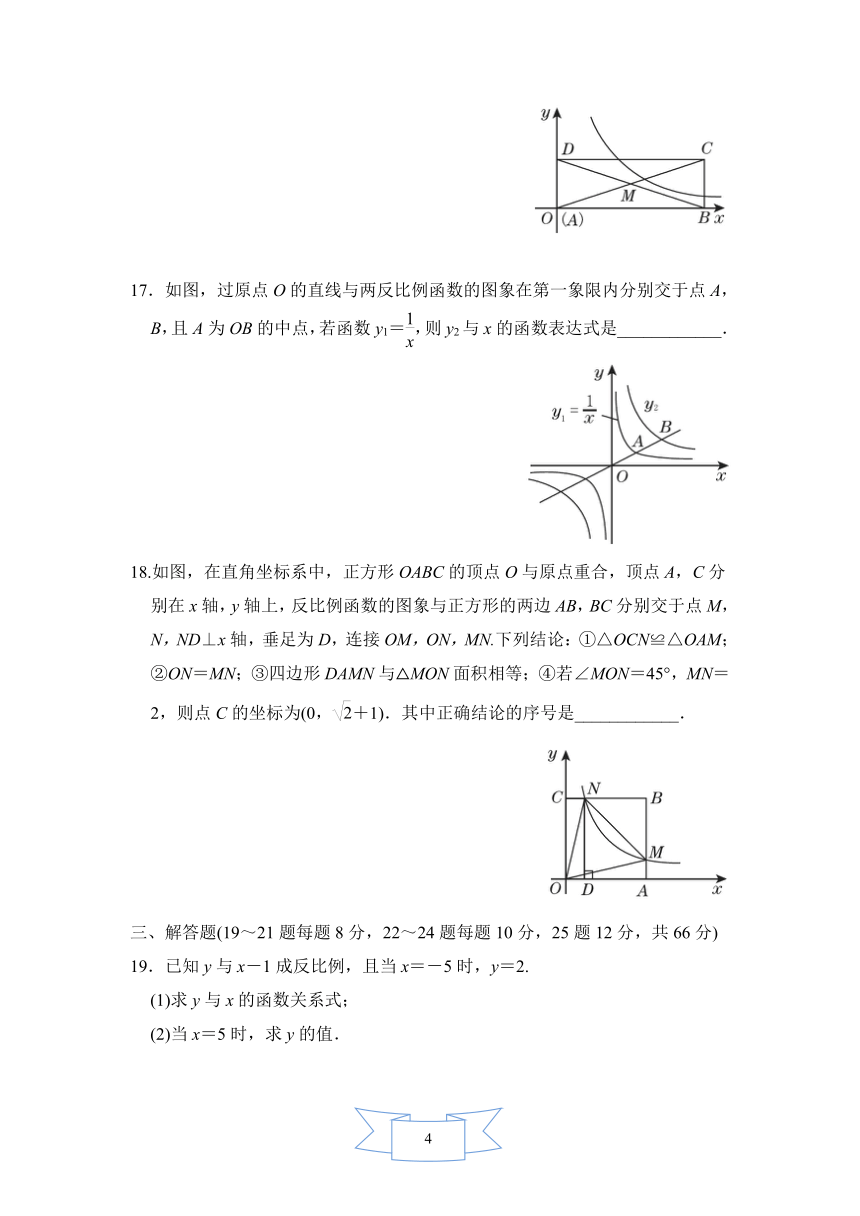
17.如图,过原点O的直线与两反比例函数的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数y1=,则y2与x的函数表达式是____________.
18.如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A,C分别在x轴,y轴上,反比例函数的图象与正方形的两边AB,BC分别交于点M,N,ND⊥x轴,垂足为D,连接OM,ON,MN.下列结论:①△OCN≌△OAM;②ON=MN;③四边形DAMN与△MON面积相等;④若∠MON=45°,MN=2,则点C的坐标为(0,+1).其中正确结论的序号是____________.
三、解答题(19~21题每题8分,22~24题每题10分,25题12分,共66分)
19.已知y与x-1成反比例,且当x=-5时,y=2.
(1)求y与x的函数关系式;
(2)当x=5时,求y的值.
20.如图,已知一次函数y=kx+b的图象与反比例函数y=的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
(1)求一次函数的表达式;
(2)求△AOB的面积.
21.已知反比例函数y=.
(1)若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2)如图,反比例函数y=(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.
22.如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-的图象交于A(-2,b),B两点.
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后,与反比例函数的图象有且只有一个公共点,求m的值.
23.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在y轴,x轴上,点B的坐标为(4,2),直线y=-x+3分别交AB,BC于点M,N,反比例函数y=的图象经过点M,N.
(1)求反比例函数的表达式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
24.教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10
℃,待加热到100
℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20
℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40
℃的开水,则他需要在什么时间段内接水?
25.如图,正比例函数y=2x的图象与反比例函数y=的图象交于A,B两点,过点A作AC⊥x轴于点C,连接BC,若△ABC的面积为2.
(1)求k的值.
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
答案
一、1.D 2.D 3.D 4.C
5.D 点拨:若k1,k2同正或同负其图象均有交点.
6.D 点拨:由题意知,反比例函数图象在第二、四象限,所以3+m<0,即m<-3.
7.C
8.C 点拨:把y=3代入y=x+2,得x=1.∴A(1,3).把点A的坐标代入y=,得k=xy=3.
9.A 点拨:设A点坐标为,B点坐标为,则C点坐标为,D点坐标为,由题意得
10.D 点拨:①由于A,B在同一反比例函数y=的图象上,则S△ODB=S△OCA=×2=1,∴①正确;②由于矩形OCMD、△ODB、△OCA的面积为定值,则四边形OAMB的面积不会发生变化,∴②正确;③连接OM,当点A是MC的中点时,S△OAM=S△OAC.
∵S△ODM=S△OCM=,
又S△ODB=S△OCA,
∴S△OBM=S△OAM,
∴S△OBD=S△OBM,
∴点B是MD的中点,
∴③正确.
二、11.y= 12.<
13.(-2,-4) 点拨:∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,∴另一个交点的坐标与点(2,4)关于原点对称,∴该点的坐标为(-2,-4).
14.1
15.y= 点拨:连接OA,则△ABP与△ABO的面积都等于6,所以反比例函数的表达式是y=.
16. 点拨:将矩形ABCD沿x轴向右平移后,过点M作ME⊥AB于点E,则AE=AB=,ME=BC=.设OA=m,则OE=OA+AE=m+,
∴M.∵点M在反比例函数y=的图象上,
∴=,解得m=.
17.y2= 18.①③④
三、19.解:(1)设y与x的函数关系式为y=,
由题意得2=,
解得k=-12.
∴y与x的函数关系式为
y=-.
(2)当x=5时,y=-=
-=-3.
20.解:(1)反比例函数y=中
x=2,则y=4,
∴点A的坐标为(2,4).
反比例函数y=中y=-2,则-2=,解得x=-4,
∴点B的坐标为(-4,-2).
∵一次函数的图象过A、B两点,
∴
解得
∴一次函数的表达式为y=x+2.
(2)令y=x+2中x=0,则y=2,
∴点C的坐标为(0,2),
∴S△AOB=OC·(xA-xB)=×2×[2-(-4)]=6.
21.
解:(1)联立方程组得kx2+4x-4=0.∵反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,∴Δ=16+16k=0,
∴k=-1.
(2)如图所示,C1平移至C2处所扫过的面积为2×3=6.
22.解:(1)根据题意,把A(-2,b)的坐标分别代入一次函数和反比例函数表达式,得解得所以一次函数的表达式为y=x+5.
(2)将直线AB向下平移m(m>0)个单位长度后,直线AB对应的函数表达式为y=x+5-m.由得x2+(5-m)x+8=0.易知Δ=(5-m)2-4××8=0,解得m=1或m=9.
23.解:(1)由题意易得点M的纵坐标为2.
将y=2代入y=-x+3,得x=2.
∴M(2,2).把点M的坐标代入y=,得k=4,
∴反比例函数的表达式是y=.
(2)由题意得S△OPM=OP·AM,
S四边形BMON=S矩形OABC-S△AOM-S△CON=4×2-2-2=4,
∵S△OPM=S四边形BMON,
∴OP·AM=4.
又易知AM=2,∴OP=4.
∴点P的坐标是(0,4)或(0,-4).
24.解:(1)当0≤x≤8时,设y=k1x+b,
将(0,20),(8,100)的坐标分别代入y=k1x+b,可求得k1=10,b=20.
∴当0≤x≤8时,y=10x+20.
当8<x≤a时,设y=,
将(8,100)的坐标代入y=,
得k2=800.
∴当8综上,当0≤x≤8时,y=10x+20;
当8<x≤a时,y=.
(2)将y=20代入y=,
解得x=40,即a=40.
(3)当y=40时,x==20.
∴要想喝到不低于40
℃的开水,x需满足8≤x≤20,即李老师要在7:38到7:50之间接水.
25.解:(1)∵正比例函数图象与反比例函数图象的两个交点关于原点对称,
∴S△AOC=S△BOC=S△ABC=1.
又∵AC⊥x轴,∴k=2.
(2)假设存在这样的点D,设点D的坐标为(m,0).
由解得
∴A(1,2),B(-1,-2).
∴AD=,
BD=,
AB==2
.
当D为直角顶点时,
∵AB=2
,∴OD=AB=.
∴D的坐标为(,0)或(-,0).
当A为直角顶点时,
由AB2+AD2=BD2,得(2
)2+(1-m)2+22=(m+1)2+22,
解得m=5,即D(5,0).当B为直角顶点时,
由BD2+AB2=AD2,得(m+1)2+22+(2
)2=(1-m)2+22,
解得m=-5,即D(-5,0).
∴存在这样的点D,使△ABD为直角三角形,点D的坐标为(,0)或(-,0)或(5,0)或(-5,0).
一、选择题(每题3分,共30分)
1.下列函数中,表示y是x的反比例函数的是( )
A.x(y+1)=1 B.y= C.y=- D.y=
2.反比例函数y=的图象经过点(3,-2),下列各点在图象上的是( )
A.(-3,-2)
B.(3,2)
C.(-2,-3)
D.(-2,3)
3.已知反比例函数y=,下列结论中不正确的是( )
A.其图象经过点(3,1)
B.其图象分别位于第一、第三象限
C.当x>0时,y随x的增大而减小
D.当x>1时,y>3
4.为了更好保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足关系式V=Sh(V≠0),则S关于h的函数图象大致是( )
5.若在同一直角坐标系中,正比例函数y=k1x与反比例函数y=的图象无交点,则有( )
A.k1+k2>0
B.k1+k2<0
C.k1k2>0
D.k1k2<0
6.已知点A(-1,y1),B(2,y2)都在双曲线y=上,且y1>y2,则m的取值范围是( )
A.m<0
B.m>0
C.m>-3
D.m<-3
7.y=ax+b与y=,其中ab<0,a,b为常数,它们在同一坐标系中的图象可以是( )
8.如图所示,直线y=x+2与双曲线y=相交于点A,点A的纵坐标为3,则k的值为( )
A.1
B.2
C.3
D.4
9.如图,A,B两点在反比例函数y=的图象上,C,D两点在反比例函数y=的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=,则k2-k1的值为( )
A.4
B.
C.
D.6
10.反比例函数y=(a>0,a为常数)和y=在第一象限内的图象如图所示,点M在y=的图象上,MC⊥x轴于点C,交y=的图象于点A;MD⊥y轴于点D,交y=的图象于点B.当点M在y=(x>0)的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,点B是MD的中点.其中正确的结论有( )
A.0个
B.1个
C.2个
D.3个
二、填空题(每题3分,共24分)
11.一个反比例函数的图象过点A(-2,-3),则这个反比例函数的表达式是________.
12.若点(2,y1),(3,y2)在函数y=-的图象上,则y1________y2(填“>”“<”或“=”).
13.已知直线y=ax(a≠0)与反比例函数y=(k≠0)的图象一个交点的坐标为(2,4),则它们另一个交点的坐标是________.
14.某闭合电路,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图表示的是该电路中电流I与电阻R之间的函数关系的图象,当电阻R为6
Ω时,电流I为________A.
15.如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,且△ABP的面积为6,则这个反比例函数的表达式为________.
16.如图,矩形ABCD在第一象限,AB在x轴的正半轴上(点A与点O重合),AB=3,BC=1,连接AC,BD,交点为M.将矩形ABCD沿x轴向右平移,当平移距离为________时,点M在反比例函数y=的图象上.
17.如图,过原点O的直线与两反比例函数的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数y1=,则y2与x的函数表达式是____________.
18.如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A,C分别在x轴,y轴上,反比例函数的图象与正方形的两边AB,BC分别交于点M,N,ND⊥x轴,垂足为D,连接OM,ON,MN.下列结论:①△OCN≌△OAM;②ON=MN;③四边形DAMN与△MON面积相等;④若∠MON=45°,MN=2,则点C的坐标为(0,+1).其中正确结论的序号是____________.
三、解答题(19~21题每题8分,22~24题每题10分,25题12分,共66分)
19.已知y与x-1成反比例,且当x=-5时,y=2.
(1)求y与x的函数关系式;
(2)当x=5时,求y的值.
20.如图,已知一次函数y=kx+b的图象与反比例函数y=的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
(1)求一次函数的表达式;
(2)求△AOB的面积.
21.已知反比例函数y=.
(1)若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2)如图,反比例函数y=(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.
22.如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-的图象交于A(-2,b),B两点.
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后,与反比例函数的图象有且只有一个公共点,求m的值.
23.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在y轴,x轴上,点B的坐标为(4,2),直线y=-x+3分别交AB,BC于点M,N,反比例函数y=的图象经过点M,N.
(1)求反比例函数的表达式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
24.教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10
℃,待加热到100
℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20
℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40
℃的开水,则他需要在什么时间段内接水?
25.如图,正比例函数y=2x的图象与反比例函数y=的图象交于A,B两点,过点A作AC⊥x轴于点C,连接BC,若△ABC的面积为2.
(1)求k的值.
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
答案
一、1.D 2.D 3.D 4.C
5.D 点拨:若k1,k2同正或同负其图象均有交点.
6.D 点拨:由题意知,反比例函数图象在第二、四象限,所以3+m<0,即m<-3.
7.C
8.C 点拨:把y=3代入y=x+2,得x=1.∴A(1,3).把点A的坐标代入y=,得k=xy=3.
9.A 点拨:设A点坐标为,B点坐标为,则C点坐标为,D点坐标为,由题意得
10.D 点拨:①由于A,B在同一反比例函数y=的图象上,则S△ODB=S△OCA=×2=1,∴①正确;②由于矩形OCMD、△ODB、△OCA的面积为定值,则四边形OAMB的面积不会发生变化,∴②正确;③连接OM,当点A是MC的中点时,S△OAM=S△OAC.
∵S△ODM=S△OCM=,
又S△ODB=S△OCA,
∴S△OBM=S△OAM,
∴S△OBD=S△OBM,
∴点B是MD的中点,
∴③正确.
二、11.y= 12.<
13.(-2,-4) 点拨:∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,∴另一个交点的坐标与点(2,4)关于原点对称,∴该点的坐标为(-2,-4).
14.1
15.y= 点拨:连接OA,则△ABP与△ABO的面积都等于6,所以反比例函数的表达式是y=.
16. 点拨:将矩形ABCD沿x轴向右平移后,过点M作ME⊥AB于点E,则AE=AB=,ME=BC=.设OA=m,则OE=OA+AE=m+,
∴M.∵点M在反比例函数y=的图象上,
∴=,解得m=.
17.y2= 18.①③④
三、19.解:(1)设y与x的函数关系式为y=,
由题意得2=,
解得k=-12.
∴y与x的函数关系式为
y=-.
(2)当x=5时,y=-=
-=-3.
20.解:(1)反比例函数y=中
x=2,则y=4,
∴点A的坐标为(2,4).
反比例函数y=中y=-2,则-2=,解得x=-4,
∴点B的坐标为(-4,-2).
∵一次函数的图象过A、B两点,
∴
解得
∴一次函数的表达式为y=x+2.
(2)令y=x+2中x=0,则y=2,
∴点C的坐标为(0,2),
∴S△AOB=OC·(xA-xB)=×2×[2-(-4)]=6.
21.
解:(1)联立方程组得kx2+4x-4=0.∵反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,∴Δ=16+16k=0,
∴k=-1.
(2)如图所示,C1平移至C2处所扫过的面积为2×3=6.
22.解:(1)根据题意,把A(-2,b)的坐标分别代入一次函数和反比例函数表达式,得解得所以一次函数的表达式为y=x+5.
(2)将直线AB向下平移m(m>0)个单位长度后,直线AB对应的函数表达式为y=x+5-m.由得x2+(5-m)x+8=0.易知Δ=(5-m)2-4××8=0,解得m=1或m=9.
23.解:(1)由题意易得点M的纵坐标为2.
将y=2代入y=-x+3,得x=2.
∴M(2,2).把点M的坐标代入y=,得k=4,
∴反比例函数的表达式是y=.
(2)由题意得S△OPM=OP·AM,
S四边形BMON=S矩形OABC-S△AOM-S△CON=4×2-2-2=4,
∵S△OPM=S四边形BMON,
∴OP·AM=4.
又易知AM=2,∴OP=4.
∴点P的坐标是(0,4)或(0,-4).
24.解:(1)当0≤x≤8时,设y=k1x+b,
将(0,20),(8,100)的坐标分别代入y=k1x+b,可求得k1=10,b=20.
∴当0≤x≤8时,y=10x+20.
当8<x≤a时,设y=,
将(8,100)的坐标代入y=,
得k2=800.
∴当8
当8<x≤a时,y=.
(2)将y=20代入y=,
解得x=40,即a=40.
(3)当y=40时,x==20.
∴要想喝到不低于40
℃的开水,x需满足8≤x≤20,即李老师要在7:38到7:50之间接水.
25.解:(1)∵正比例函数图象与反比例函数图象的两个交点关于原点对称,
∴S△AOC=S△BOC=S△ABC=1.
又∵AC⊥x轴,∴k=2.
(2)假设存在这样的点D,设点D的坐标为(m,0).
由解得
∴A(1,2),B(-1,-2).
∴AD=,
BD=,
AB==2
.
当D为直角顶点时,
∵AB=2
,∴OD=AB=.
∴D的坐标为(,0)或(-,0).
当A为直角顶点时,
由AB2+AD2=BD2,得(2
)2+(1-m)2+22=(m+1)2+22,
解得m=5,即D(5,0).当B为直角顶点时,
由BD2+AB2=AD2,得(m+1)2+22+(2
)2=(1-m)2+22,
解得m=-5,即D(-5,0).
∴存在这样的点D,使△ABD为直角三角形,点D的坐标为(,0)或(-,0)或(5,0)或(-5,0).
