鲁教版(五四制)数学九年级上册第四章投影与视图达标测试卷 含答案
文档属性
| 名称 | 鲁教版(五四制)数学九年级上册第四章投影与视图达标测试卷 含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 329.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 17:55:25 | ||
图片预览



文档简介
第四章达标测试卷
一、选择题(每题3分,共30分)
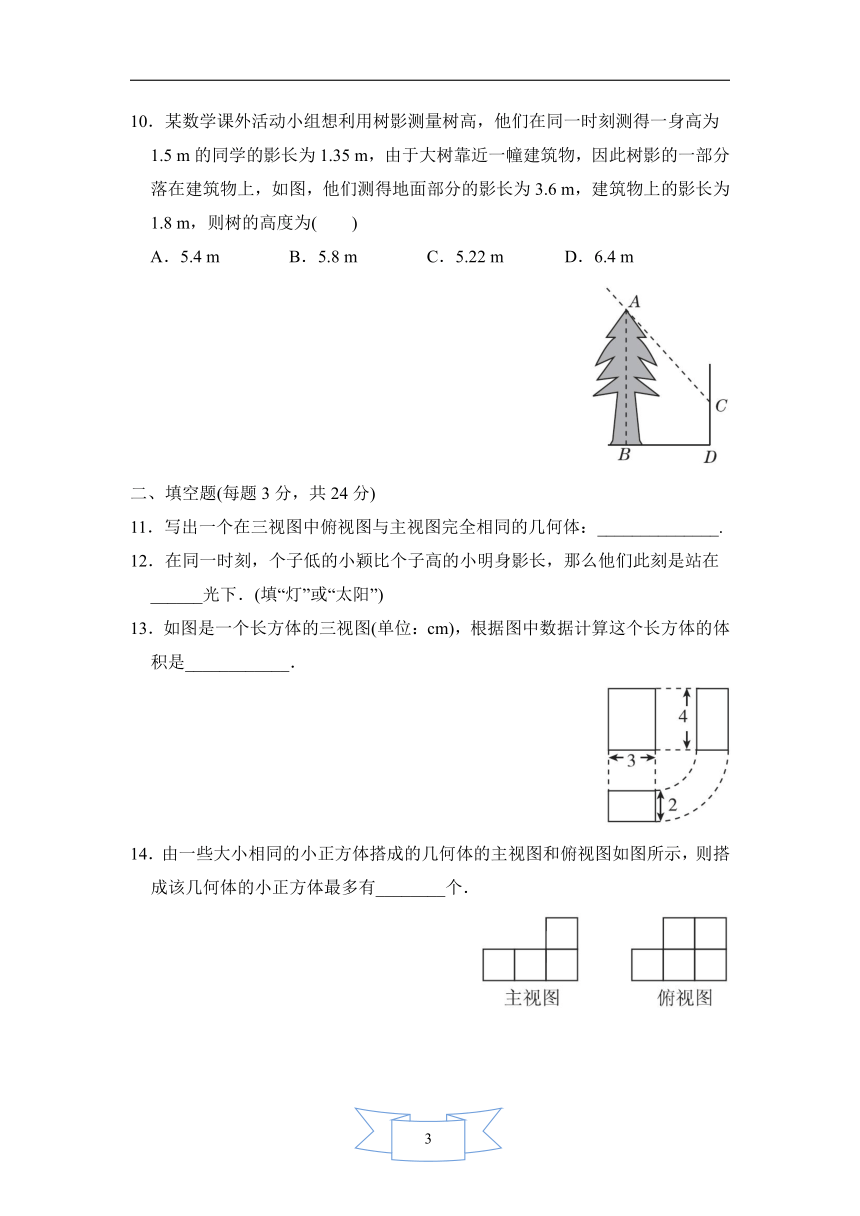
1.下列几何体中,俯视图为矩形的是( )
2.如果在同一时刻的阳光下,小莉的影子比小玉的影子长,那么在同一路灯下( )
A.小莉的影子比小玉的影子长
B.小莉的影子比小玉的影子短
C.小莉的影子与小玉的影子一样长
D.无法判断谁的影子长
3.如图是一个几何体的三视图,则此几何体为( )
4.如图,位似图形由三角尺与其在灯光照射下的中心投影组成,相似比为2∶5,且三角尺一边长为8
cm,则投影三角形的对应边长为( )
A.8
cm
B.20
cm
C.3.2
cm
D.10
cm
5.李刚同学拿一个矩形木框在阳光下摆弄,矩形木框在地面上形成的投影不可能是图中的( )
6.如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图改变,左视图改变
D.主视图改变,左视图不变
7.如图是几个一样的小正方体摆出的立体图形的三视图,由三视图可知小正方体的个数为( )
A.6个
B.5个
C.4个
D.3个
8.如图(1)、(2)、(3)、(4)是一天中四个不同时刻木杆在地面上的影子的示意图,将它们按时间先后顺序排列正确的一项是( )
A.(4)、(3)、(1)、(2)
B.(1)、(2)、(3)、(4)
C.(2)、(3)、(1)、(4)
D.(3)、(1)、(4)、(2)
9.某学校小卖部货架上摆放着某品牌的方便面,它们的三视图如图所示,则货架上的方便面至少有( )
A.7盒
B.8盒
C.9盒
D.10盒
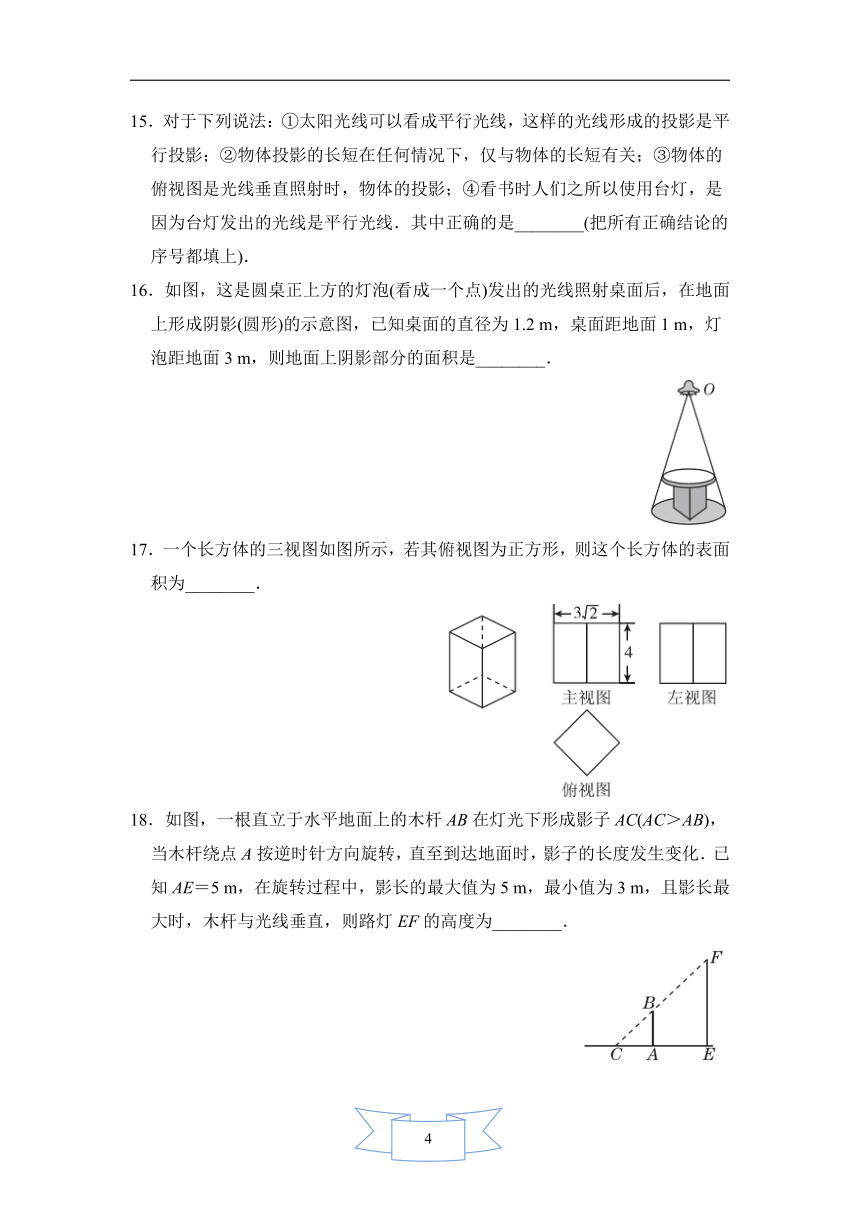
10.某数学课外活动小组想利用树影测量树高,他们在同一时刻测得一身高为1.5
m的同学的影长为1.35
m,由于大树靠近一幢建筑物,因此树影的一部分落在建筑物上,如图,他们测得地面部分的影长为3.6
m,建筑物上的影长为1.8
m,则树的高度为( )
A.5.4
m
B.5.8
m
C.5.22
m
D.6.4
m
二、填空题(每题3分,共24分)
11.写出一个在三视图中俯视图与主视图完全相同的几何体:______________.
12.在同一时刻,个子低的小颖比个子高的小明身影长,那么他们此刻是站在______光下.(填“灯”或“太阳”)
13.如图是一个长方体的三视图(单位:cm),根据图中数据计算这个长方体的体积是____________.
14.由一些大小相同的小正方体搭成的几何体的主视图和俯视图如图所示,则搭成该几何体的小正方体最多有________个.
15.对于下列说法:①太阳光线可以看成平行光线,这样的光线形成的投影是平行投影;②物体投影的长短在任何情况下,仅与物体的长短有关;③物体的俯视图是光线垂直照射时,物体的投影;④看书时人们之所以使用台灯,是因为台灯发出的光线是平行光线.其中正确的是________(把所有正确结论的序号都填上).
16.如图,这是圆桌正上方的灯泡(看成一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2
m,桌面距地面1
m,灯泡距地面3
m,则地面上阴影部分的面积是________.
17.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的表面积为________.
18.如图,一根直立于水平地面上的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5
m,在旋转过程中,影长的最大值为5
m,最小值为3
m,且影长最大时,木杆与光线垂直,则路灯EF的高度为________.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.如图是一支架(一种小零件),支架的两个台阶的高度和宽度都为同一长度,试画出它的三视图.
20.由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形.
21.如图,小华、小军、小丽同时站在路灯下,其中小军和小丽的影子分别是AB,CD.
(1)请你在图中画出路灯灯泡所在的位置(用点P表示);
(2)画出小华此时在路灯下的影子(用线段EF表示).
22.如图,小美利用所学的数学知识测量旗杆AB的高度.
(1)请你根据小美在阳光下的投影,画出此时旗杆AB在阳光下的投影;
(2)已知小美的身高为1.54
m,在同一时刻测得小美和旗杆AB的投影长分别为0.77
m和6
m,求旗杆AB的高.
23.如图是一个几何体的三视图.(单位:cm)
(1)组成该几何体的两部分分别是什么几何体?
(2)求该几何体的体积.(结果保留π)
24.为加快新农村建设,某市投入资金建设新型农村社区.图为住宅区内的两幢楼,它们的高AB=CD=30
m,现需了解甲楼对乙楼采光情况的影响.当太阳光线与水平线的夹角为30°时.试求:
(1)若两楼间的距离AC=24
m,那么甲楼的影子落在乙楼上有多高.(结果保留根号)
(2)若甲楼的影子刚好不影响乙楼,那么两楼之间的距离应当有多远.(结果保留根号)
答案
一、1.C 2.D 3.B
4.B 点拨:设所求投影三角形的对应边长为x
cm,则有=,解得x=20.
5.D
6.D 点拨:移走之前,主视图为,俯视图为,左视图为,移走之后,主视图为,俯视图为,左视图为,故只有左视图不变.
7.C 点拨:综合三视图,这个立体图形的底层应该有3个,第二层应该有1个小正方体,因此构成这个立体图形的小正方体的个数是3+1=4(个).
8.A
9.A 点拨:当货架上的方便面盒数最少时,如图所示,数字表示该位置叠放的方便面盒数,因此至少有7盒.
10.B 点拨:如图,分别延长AC,BD交于点E.
∵BD=3.6
m,CD=1.8
m,且同一时刻测得一身高为1.5
m的同学的影长为1.35
m,∴=,即=.∴DE=1.62
m.∵CD∥AB,∴∠ABD=∠CDE,∠BAC=∠DCE.∴△ABE∽△CDE.∴=,即=.解得AB=5.8
m.
二、11.正方体(答案不唯一)
12.灯 点拨:在灯光下,离点光源越近,影子越短;离点光源越远,影子越长.所以他们是站在灯光下.
13.24
cm3
14.7 点拨:根据题意得搭成该几何体的小正方体最多有1+1+1+2+2=7(个).
15.① 16.0.81π
m2
17.66 点拨:由三视图的定义及勾股定理知长方体的长与宽均为3,高为4,故表面积为2×(3×3+3×4+3×4)=66.
18.7.5
m 点拨:当木杆旋转到达地面时,影长最短,等于AB的长.
∵影长的最小值为3
m,
∴AB=3
m.∵影长最大时,木杆与光线垂直(如图),此时AC=5
m,
∴BC==4
m.
∵∠CBA=∠CEF=90°,∠C=∠C,∴△CAB∽△CFE.
∴=,即=
.
∴EF=7.5
m.
三、19.解:如图所示.
20.解:如图所示.
点拨:由左、俯视图可判断,该几何体共两层,底层有3×3=9(个)小正方体,上层中间一行有小正方体,若使主视图为轴对称图形使中间一行、中间一列有一个小正方体即可,答案不唯一.
21.解:如图.(1)点P就是所求的点.(2)EF就是小华此时在路灯下的影子.
22.解:(1)如图.BC为此时旗杆AB在阳光下的投影.
(2)如图,因为DE,AB都垂直于地面,且光线DF∥AC,
所以∠DEF=∠ABC=90°,∠DFE=∠ACB.
所以△DEF∽△ABC.
所以=,即=.
所以AB=12
m.
因此旗杆AB的高为12
m.
23.解:(1)由题图可知,该几何体的下部分是长方体,上部分是圆柱.
(2)该几何体的体积为30×40×25+π×(20÷2)2×32=30
000+3
200π(cm3).
24.解:(1)∵AB=CD=30
m,BA⊥AC,CD⊥AC,∴四边形ABDC是矩形.∴BD=AC=24
m,∠BDE=90°.∵∠DBE=30°,
∴设DE=x
m,则BE=2x
m.
∴在Rt△BDE中,BD===x(m).
∴x=24,解得x=8
.
∴EC=CD-DE=(30-8
)m,
即甲楼的影子落在乙楼上有(30-8
)m高.
(2)如图.当太阳光照射到C时,甲楼的影子刚好不影响乙楼.在Rt△ABC中,AB=30
m,
∠ACB=30°,
∴BC=2AB=60
m.
在Rt△ABC中,由勾股定理得
AC===30
(m).
∴若甲楼的影子刚好不影响乙楼时,两楼之间的距离应当为30
m.
一、选择题(每题3分,共30分)
1.下列几何体中,俯视图为矩形的是( )
2.如果在同一时刻的阳光下,小莉的影子比小玉的影子长,那么在同一路灯下( )
A.小莉的影子比小玉的影子长
B.小莉的影子比小玉的影子短
C.小莉的影子与小玉的影子一样长
D.无法判断谁的影子长
3.如图是一个几何体的三视图,则此几何体为( )
4.如图,位似图形由三角尺与其在灯光照射下的中心投影组成,相似比为2∶5,且三角尺一边长为8
cm,则投影三角形的对应边长为( )
A.8
cm
B.20
cm
C.3.2
cm
D.10
cm
5.李刚同学拿一个矩形木框在阳光下摆弄,矩形木框在地面上形成的投影不可能是图中的( )
6.如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图改变,左视图改变
D.主视图改变,左视图不变
7.如图是几个一样的小正方体摆出的立体图形的三视图,由三视图可知小正方体的个数为( )
A.6个
B.5个
C.4个
D.3个
8.如图(1)、(2)、(3)、(4)是一天中四个不同时刻木杆在地面上的影子的示意图,将它们按时间先后顺序排列正确的一项是( )
A.(4)、(3)、(1)、(2)
B.(1)、(2)、(3)、(4)
C.(2)、(3)、(1)、(4)
D.(3)、(1)、(4)、(2)
9.某学校小卖部货架上摆放着某品牌的方便面,它们的三视图如图所示,则货架上的方便面至少有( )
A.7盒
B.8盒
C.9盒
D.10盒
10.某数学课外活动小组想利用树影测量树高,他们在同一时刻测得一身高为1.5
m的同学的影长为1.35
m,由于大树靠近一幢建筑物,因此树影的一部分落在建筑物上,如图,他们测得地面部分的影长为3.6
m,建筑物上的影长为1.8
m,则树的高度为( )
A.5.4
m
B.5.8
m
C.5.22
m
D.6.4
m
二、填空题(每题3分,共24分)
11.写出一个在三视图中俯视图与主视图完全相同的几何体:______________.
12.在同一时刻,个子低的小颖比个子高的小明身影长,那么他们此刻是站在______光下.(填“灯”或“太阳”)
13.如图是一个长方体的三视图(单位:cm),根据图中数据计算这个长方体的体积是____________.
14.由一些大小相同的小正方体搭成的几何体的主视图和俯视图如图所示,则搭成该几何体的小正方体最多有________个.
15.对于下列说法:①太阳光线可以看成平行光线,这样的光线形成的投影是平行投影;②物体投影的长短在任何情况下,仅与物体的长短有关;③物体的俯视图是光线垂直照射时,物体的投影;④看书时人们之所以使用台灯,是因为台灯发出的光线是平行光线.其中正确的是________(把所有正确结论的序号都填上).
16.如图,这是圆桌正上方的灯泡(看成一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2
m,桌面距地面1
m,灯泡距地面3
m,则地面上阴影部分的面积是________.
17.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的表面积为________.
18.如图,一根直立于水平地面上的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5
m,在旋转过程中,影长的最大值为5
m,最小值为3
m,且影长最大时,木杆与光线垂直,则路灯EF的高度为________.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.如图是一支架(一种小零件),支架的两个台阶的高度和宽度都为同一长度,试画出它的三视图.
20.由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形.
21.如图,小华、小军、小丽同时站在路灯下,其中小军和小丽的影子分别是AB,CD.
(1)请你在图中画出路灯灯泡所在的位置(用点P表示);
(2)画出小华此时在路灯下的影子(用线段EF表示).
22.如图,小美利用所学的数学知识测量旗杆AB的高度.
(1)请你根据小美在阳光下的投影,画出此时旗杆AB在阳光下的投影;
(2)已知小美的身高为1.54
m,在同一时刻测得小美和旗杆AB的投影长分别为0.77
m和6
m,求旗杆AB的高.
23.如图是一个几何体的三视图.(单位:cm)
(1)组成该几何体的两部分分别是什么几何体?
(2)求该几何体的体积.(结果保留π)
24.为加快新农村建设,某市投入资金建设新型农村社区.图为住宅区内的两幢楼,它们的高AB=CD=30
m,现需了解甲楼对乙楼采光情况的影响.当太阳光线与水平线的夹角为30°时.试求:
(1)若两楼间的距离AC=24
m,那么甲楼的影子落在乙楼上有多高.(结果保留根号)
(2)若甲楼的影子刚好不影响乙楼,那么两楼之间的距离应当有多远.(结果保留根号)
答案
一、1.C 2.D 3.B
4.B 点拨:设所求投影三角形的对应边长为x
cm,则有=,解得x=20.
5.D
6.D 点拨:移走之前,主视图为,俯视图为,左视图为,移走之后,主视图为,俯视图为,左视图为,故只有左视图不变.
7.C 点拨:综合三视图,这个立体图形的底层应该有3个,第二层应该有1个小正方体,因此构成这个立体图形的小正方体的个数是3+1=4(个).
8.A
9.A 点拨:当货架上的方便面盒数最少时,如图所示,数字表示该位置叠放的方便面盒数,因此至少有7盒.
10.B 点拨:如图,分别延长AC,BD交于点E.
∵BD=3.6
m,CD=1.8
m,且同一时刻测得一身高为1.5
m的同学的影长为1.35
m,∴=,即=.∴DE=1.62
m.∵CD∥AB,∴∠ABD=∠CDE,∠BAC=∠DCE.∴△ABE∽△CDE.∴=,即=.解得AB=5.8
m.
二、11.正方体(答案不唯一)
12.灯 点拨:在灯光下,离点光源越近,影子越短;离点光源越远,影子越长.所以他们是站在灯光下.
13.24
cm3
14.7 点拨:根据题意得搭成该几何体的小正方体最多有1+1+1+2+2=7(个).
15.① 16.0.81π
m2
17.66 点拨:由三视图的定义及勾股定理知长方体的长与宽均为3,高为4,故表面积为2×(3×3+3×4+3×4)=66.
18.7.5
m 点拨:当木杆旋转到达地面时,影长最短,等于AB的长.
∵影长的最小值为3
m,
∴AB=3
m.∵影长最大时,木杆与光线垂直(如图),此时AC=5
m,
∴BC==4
m.
∵∠CBA=∠CEF=90°,∠C=∠C,∴△CAB∽△CFE.
∴=,即=
.
∴EF=7.5
m.
三、19.解:如图所示.
20.解:如图所示.
点拨:由左、俯视图可判断,该几何体共两层,底层有3×3=9(个)小正方体,上层中间一行有小正方体,若使主视图为轴对称图形使中间一行、中间一列有一个小正方体即可,答案不唯一.
21.解:如图.(1)点P就是所求的点.(2)EF就是小华此时在路灯下的影子.
22.解:(1)如图.BC为此时旗杆AB在阳光下的投影.
(2)如图,因为DE,AB都垂直于地面,且光线DF∥AC,
所以∠DEF=∠ABC=90°,∠DFE=∠ACB.
所以△DEF∽△ABC.
所以=,即=.
所以AB=12
m.
因此旗杆AB的高为12
m.
23.解:(1)由题图可知,该几何体的下部分是长方体,上部分是圆柱.
(2)该几何体的体积为30×40×25+π×(20÷2)2×32=30
000+3
200π(cm3).
24.解:(1)∵AB=CD=30
m,BA⊥AC,CD⊥AC,∴四边形ABDC是矩形.∴BD=AC=24
m,∠BDE=90°.∵∠DBE=30°,
∴设DE=x
m,则BE=2x
m.
∴在Rt△BDE中,BD===x(m).
∴x=24,解得x=8
.
∴EC=CD-DE=(30-8
)m,
即甲楼的影子落在乙楼上有(30-8
)m高.
(2)如图.当太阳光照射到C时,甲楼的影子刚好不影响乙楼.在Rt△ABC中,AB=30
m,
∠ACB=30°,
∴BC=2AB=60
m.
在Rt△ABC中,由勾股定理得
AC===30
(m).
∴若甲楼的影子刚好不影响乙楼时,两楼之间的距离应当为30
m.
