人教版高中物理必修2第七章第4节 重力势能(共18张PPT)
文档属性
| 名称 | 人教版高中物理必修2第七章第4节 重力势能(共18张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-11 20:45:38 | ||
图片预览





文档简介
(共18张PPT)
第七章
机械能守恒定律
4
重力势能
物体由于被举高而具有的能量叫
重力势能.
重力势能的大小与哪些因素有关?
又如何定量表示呢?
用自己的课本做如下实验
1)同一课本从不同高度下落到自己手
上,感觉
?
?
?
2)不同质量的课本从同一高度下落到自己手上,感觉
?
?
?
结论:重力相同,高度差越大,重力势能越大;
同一高度,重力越大,重力势能越大。重力势能的表达式应该符合这些特征。
5
控制变量法
探究:重力做功的特点
问题:小朋友沿不同路径从滑梯上端到下端,请判
断重力做功情况?
一、重力做功
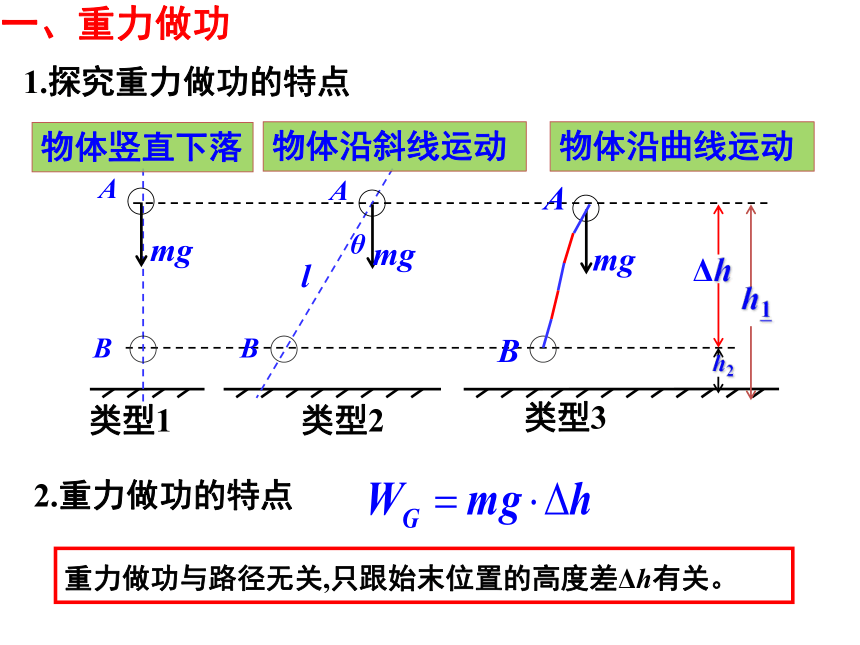
1.探究重力做功的特点
物体竖直下落
物体沿斜线运动
物体沿曲线运动
2.重力做功的特点
重力做功与路径无关,只跟始末位置的高度差Δh有关。
1.重力做功大小只与重力和物体高度变化有关,与受其他力及运动状态均无关.
2.物体下降时重力做正功,物体上升时重力做负功.
3.在一些往复运动或多个运动过程的复杂问题中求重力做功时,利用重力做功的特点,可以省去大量中间过程,一步求解.
2.重力势能的表达式
即:物体的重力势能等于物体的重量和它的高度的乘积。
二、重力势能
1.定义:物体由于被举高而使物体具有的能量叫重力势能。
1.重力做功与重力势能变化的关系
WG=Ep1-Ep2=-ΔEp
2.重力势能的相对性
物体的重力势能总是相对于某一水平参考面,选不同的参考面,物体重力势能的数值是不同的.故在计算重力势能时,必须首先选取参考平面.
3.重力势能是标量,但有正负之分,物体在零势能面上方,物体的重力势能是正值,表示物体的重力势能比在参考平面上时要多,物体在零势能面下方,物体的重力势能是负值,表示物体的重力势能比在参考平面上时要少.
4.重力势能的变化量与参考平面的选择无关.
思考并回答以下问题:
1.什么叫参考平面?在参考平面,物体的重力势能是多少?
2.通常情况下,如何选取参考平面?
3.对选定的参考平面而言,什么情况下
重力势能为正值?什么情况下重力势能为负值?
想一想:重力势能跟重力做功密切相关,
如果没有了重力,物体还有重力势能吗?
没有!
提示:
严格地说,重力势能是地球与物体所组成的“系统”所共有的,平常所说的“物体”的重力势能,只是一种简化的说法。
三、重力做功与重力势能变化的关系
物体向下运动,重力做___功,重力势能____
。
物体向上运动,重力做___功,重力势能____
。
正
减少
负
增加
正功
mgh
负功
-mgh
减少
mgh
增加
mgh
重力做的功等于重力势能的减少
物体克服重力做的功等于重力势能的增加
重力做功WG
(正、负)
重力势能EP
(增加、减少)
重力做功和重力势能变化的关系
物体
上升
物体
下降
如图,质量0.5kg的小球,从桌面以上h1=1.2m的A点落到地面的B点,桌面高h2=0.8m.请按要求填写下表.并思考
(g=10m/s2)
6J
10J
-4J
0
10J
10J
减少10J
减少10J
选取不同的参考平面,物体的重力势能EP的数值不同
对一个确定的过程,WG和△EP是确定的,与参考面的选择无关,只取决于两点间的高度差
课堂练习
参考
平面
小球在A点重力势能
小球在B点重力势能
下落过程小球重力做功
下落过程小球重力势能变化
桌面
地面
巩固训练
关于重力做功和物体的重力势能,下列说法正确的是:
A、当重力对物体做正功时,物体的重力势能一定减少;
B、地球上物体一个物体的重力势能都有一个确定值;
C、重力势能等于零的物体,一定不会对别的物体做功
;
D、重力做功的多少与参考平面的选取无关。
(AD)
例1
如图所示,一粗糙的四分之一圆弧轨道,半径为R,轨道圆心O)与A点等高。一质量为m的小球在不另外施力的情况下,能以速度v沿轨道自A点匀速率运动到B点,取小球在A点时为计时起点,且此时的重力势能为零,重力加速度为g,
则在此过程中,下列说法正确的是
A.从A点到达底端过程,重力做功的功率先增后减
B.重力做的功等于小球克服摩擦力做的功
C.小球重力势能随时间的变化关系为E?p?=mgRsin
D.小球重力做功随时间的变化关系为WG=mgRsin
重力势能的计算(软体,流体)
方法总结:由于物体的重力势能等于物体的重力与物体的重心相对于参考平面的高度的乘积,因此,确定物体的重力势能时,需分析物体的重心所在位置.当物体整体的重心位置发生变化或者不便确定时,可考虑用分段法确定各部分物体的重力势能,然后再确定整体的重力势能.
例2:如图甲所示,质量为m、长度为l的均质铁链的一半搁在倾角为30°的粗糙斜面上,其余部分竖直下垂.在铁链下滑至整条铁链刚好全部离开斜面的过程中,铁链的重力势能减少了多少?
解:如图乙所示,由于初、末状态BB’部分均有铁链,故可以等效为B’C’部分由AB部分直接填补而来,所以:
答案
变式训练:如图所示,有一质量为m、长为L的均匀金属链条,一半长度在光滑斜面上,斜面倾角为θ,另一半长度沿竖直方向下垂在空中,当链条从静止开始释放后链条滑动,以斜面最高点为重力势能的零点,则:
(1)开始时和链条刚好从右侧全部滑出斜面时重力势能各是多大?
(2)重力在此过程中做了多少功?
第七章
机械能守恒定律
4
重力势能
物体由于被举高而具有的能量叫
重力势能.
重力势能的大小与哪些因素有关?
又如何定量表示呢?
用自己的课本做如下实验
1)同一课本从不同高度下落到自己手
上,感觉
?
?
?
2)不同质量的课本从同一高度下落到自己手上,感觉
?
?
?
结论:重力相同,高度差越大,重力势能越大;
同一高度,重力越大,重力势能越大。重力势能的表达式应该符合这些特征。
5
控制变量法
探究:重力做功的特点
问题:小朋友沿不同路径从滑梯上端到下端,请判
断重力做功情况?
一、重力做功
1.探究重力做功的特点
物体竖直下落
物体沿斜线运动
物体沿曲线运动
2.重力做功的特点
重力做功与路径无关,只跟始末位置的高度差Δh有关。
1.重力做功大小只与重力和物体高度变化有关,与受其他力及运动状态均无关.
2.物体下降时重力做正功,物体上升时重力做负功.
3.在一些往复运动或多个运动过程的复杂问题中求重力做功时,利用重力做功的特点,可以省去大量中间过程,一步求解.
2.重力势能的表达式
即:物体的重力势能等于物体的重量和它的高度的乘积。
二、重力势能
1.定义:物体由于被举高而使物体具有的能量叫重力势能。
1.重力做功与重力势能变化的关系
WG=Ep1-Ep2=-ΔEp
2.重力势能的相对性
物体的重力势能总是相对于某一水平参考面,选不同的参考面,物体重力势能的数值是不同的.故在计算重力势能时,必须首先选取参考平面.
3.重力势能是标量,但有正负之分,物体在零势能面上方,物体的重力势能是正值,表示物体的重力势能比在参考平面上时要多,物体在零势能面下方,物体的重力势能是负值,表示物体的重力势能比在参考平面上时要少.
4.重力势能的变化量与参考平面的选择无关.
思考并回答以下问题:
1.什么叫参考平面?在参考平面,物体的重力势能是多少?
2.通常情况下,如何选取参考平面?
3.对选定的参考平面而言,什么情况下
重力势能为正值?什么情况下重力势能为负值?
想一想:重力势能跟重力做功密切相关,
如果没有了重力,物体还有重力势能吗?
没有!
提示:
严格地说,重力势能是地球与物体所组成的“系统”所共有的,平常所说的“物体”的重力势能,只是一种简化的说法。
三、重力做功与重力势能变化的关系
物体向下运动,重力做___功,重力势能____
。
物体向上运动,重力做___功,重力势能____
。
正
减少
负
增加
正功
mgh
负功
-mgh
减少
mgh
增加
mgh
重力做的功等于重力势能的减少
物体克服重力做的功等于重力势能的增加
重力做功WG
(正、负)
重力势能EP
(增加、减少)
重力做功和重力势能变化的关系
物体
上升
物体
下降
如图,质量0.5kg的小球,从桌面以上h1=1.2m的A点落到地面的B点,桌面高h2=0.8m.请按要求填写下表.并思考
(g=10m/s2)
6J
10J
-4J
0
10J
10J
减少10J
减少10J
选取不同的参考平面,物体的重力势能EP的数值不同
对一个确定的过程,WG和△EP是确定的,与参考面的选择无关,只取决于两点间的高度差
课堂练习
参考
平面
小球在A点重力势能
小球在B点重力势能
下落过程小球重力做功
下落过程小球重力势能变化
桌面
地面
巩固训练
关于重力做功和物体的重力势能,下列说法正确的是:
A、当重力对物体做正功时,物体的重力势能一定减少;
B、地球上物体一个物体的重力势能都有一个确定值;
C、重力势能等于零的物体,一定不会对别的物体做功
;
D、重力做功的多少与参考平面的选取无关。
(AD)
例1
如图所示,一粗糙的四分之一圆弧轨道,半径为R,轨道圆心O)与A点等高。一质量为m的小球在不另外施力的情况下,能以速度v沿轨道自A点匀速率运动到B点,取小球在A点时为计时起点,且此时的重力势能为零,重力加速度为g,
则在此过程中,下列说法正确的是
A.从A点到达底端过程,重力做功的功率先增后减
B.重力做的功等于小球克服摩擦力做的功
C.小球重力势能随时间的变化关系为E?p?=mgRsin
D.小球重力做功随时间的变化关系为WG=mgRsin
重力势能的计算(软体,流体)
方法总结:由于物体的重力势能等于物体的重力与物体的重心相对于参考平面的高度的乘积,因此,确定物体的重力势能时,需分析物体的重心所在位置.当物体整体的重心位置发生变化或者不便确定时,可考虑用分段法确定各部分物体的重力势能,然后再确定整体的重力势能.
例2:如图甲所示,质量为m、长度为l的均质铁链的一半搁在倾角为30°的粗糙斜面上,其余部分竖直下垂.在铁链下滑至整条铁链刚好全部离开斜面的过程中,铁链的重力势能减少了多少?
解:如图乙所示,由于初、末状态BB’部分均有铁链,故可以等效为B’C’部分由AB部分直接填补而来,所以:
答案
变式训练:如图所示,有一质量为m、长为L的均匀金属链条,一半长度在光滑斜面上,斜面倾角为θ,另一半长度沿竖直方向下垂在空中,当链条从静止开始释放后链条滑动,以斜面最高点为重力势能的零点,则:
(1)开始时和链条刚好从右侧全部滑出斜面时重力势能各是多大?
(2)重力在此过程中做了多少功?
