人教版数学七年级下册 第九章不等式与不等式组 复习课件(共30张PPT)
文档属性
| 名称 | 人教版数学七年级下册 第九章不等式与不等式组 复习课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 768.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 20:32:09 | ||
图片预览










文档简介
(共30张PPT)
第九章
不等式与不等式组
复习课
人教版数学七下
2020.6.10
by
wyj
学习目标
学习目标
1.熟记不等式的基本性质.
2.能熟练地解一元一次不等式和一元一次不等式组,并会运用一元一次不等式的知识解决实际问题.
3.通过解一元一次不等式(组),学会数形结合、分类讨论等数学思想.
重点
一元一次不等式(组)的解法
一、知识梳理
核心梳理
1.使不等式成立的
叫做不等式的解;不等式的
组成这个不等式的解集.
未知数的值
一个未知数
2.一元一次不等式:只含有
,并且未知数的最高次数是
.
所有的解
1
二、知识梳理
3.不等式的性质:
同一个数(或式子)
性质1:不等式两边都加(或减)
,不等号的方向
;
性质2:不等式的两边都乘(或除以)
,不等号的方向______.
性质3:不等式的两边都乘(或除以)
,不等号的方向______.?
同一个正数
同一个负数
不变
不变
改变
一、知识梳理
4.解一元一次不等式的一般步骤为:
(1)
(运用不等式的性质3,注意不要
),
漏乘不含分母的项
去分母
去括号
(2)
,
移项
合并同类项
相反数
(3)
(运用不等式的性质1,注意:被移的项要变为原来的
),
(4)
,
(5)
(运用不等式的性质2、3,注意何时需要改变不等号方向),
系数化为1
(6)把解集表示在数轴上.(注意:空心、实心小圆圈的区别;“>”“≥”向右拐,“<”“≤”向左拐)
5.解一元一次不等式组的步骤:
(1)
;
求出不等式组中每个不等式的解集
借助数轴找出各解集的公共部分
(2)
;
(3)
;
写出不等式组的解集
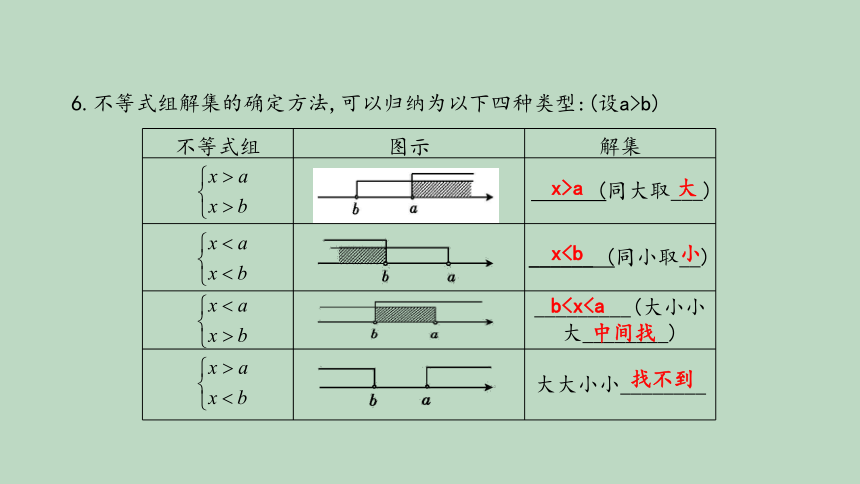
6.不等式组解集的确定方法,可以归纳为以下四种类型:(设a>b)
xbx>a
不等式组
图示
解集
(同大取___)
______
(同小取__)
_________(大小小大________)
大大小小________
大
小
中间找
找不到
7.列一元一次不等式解应用题的一般步骤:
(1)审题;
(2)
;
设未知数
找不等关系
(3)
,列不等式
(4)
;
解不等式
(5)检验并作答.
活动:下列式子中,一元一次不等式有(
)
①3x-1≥4
②
2+3x>6
③
3-
<5
④
⑤
⑥
x+xy≥y2
⑦x>0
A.5个
B.4个
C.6个
D.3个
A
√
√
×
√
√
×
√
探究一:不等式及其相关概念
二、知识应用
【归纳总结】一元一次不等式的概念含几个要点:
(3)只含有一个未知数,且含有未知数的项的最高次数为1.
(2)不等号两边都是关于未知数的整式;
(1)用不等号连接;
探究二:解不等式(组)
活动1:解不等式:x+
>1-
.
解:去分母,得8x+3(x+1)>8-4(x-5),
去括号,得8x+3x+3>8-4x+20,
移项、合并同类项,得15x>25,
系数化为1,得x>
.
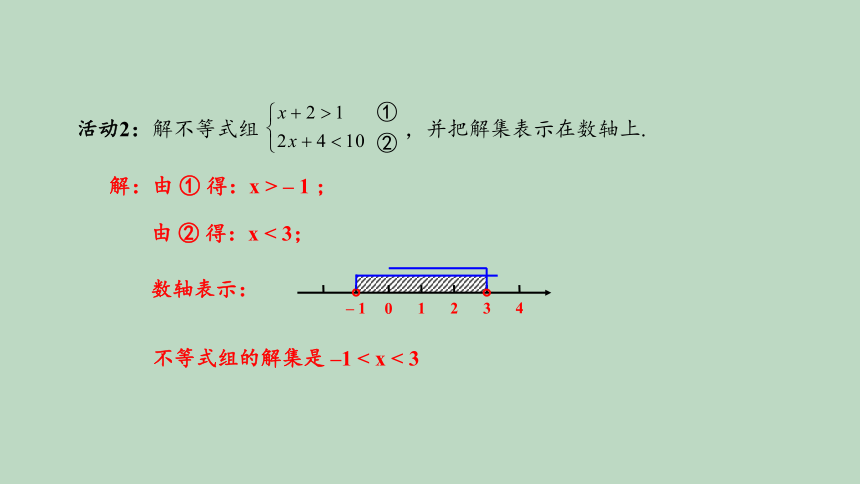
解:由
①
得:x
>
–
1
;
活动2:解不等式组
,并把解集表示在数轴上.
①②
由
②
得:x
<
3;
–
1
0
1
2
3
4
数轴表示:
不等式组的解集是
–1
<
x
<
3
探究三:列不等式解应用题
活动:春运期间,某汽车站设有6个检票口,假设有120名乘客要上车,启用3个检票口,4分钟全部检查完.假若有180名乘客要上车,要在5分钟内全部检查完,则至少得启用几个检票口?
解:
要启用x个检票口,根据题意,得:
因为x取整数,所以x=4.
故至少启用4个检票口.
x>
,解得x>3.6.
D
3.某品牌电脑的成本价为2400元,售价为2800元,该商店准备举行打折促销
活动,要求利润率不低于5%,如果将这种品牌的电脑打x折销售,则下列不
等式中能正确表示该商店的促销方式的是( )
A.2800x≥2400×5%
B.2800x﹣2400≥2400×5%
C.2800×
≥2400×5%
D.2800×
﹣2400≥2400×5%
4.一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数.
解:
设小朋友总共有x人,由此可得不等式组
3x+4-4(x-1)≥0,
3x+4-4(x-1)<3;
解得5所以x=6,7,8.
所以有三种可能:
因为x是整数,
①小朋友有6人,玩具有22件;
②小朋友有7人,玩具有25件;
③小朋友有8人,玩具有28件
二、易错点辨析
1
易错点
不等式变形后忘记改变不等号的方向
防错警示:
本题的易错点为在应用不等式的性质3将不等式变形时,忘记改变不等号的方向.
2
易错点
忽略不等式中字母取0的特殊情况
防错警示:
3
易错点
去分母时漏乘常数项
防错警示:
去分母时,不等式的两边的各项都应乘各分泌的最小公倍数,不要漏乘常数项.
4
易错点
去分母时忽略分数线的括号作用
防错警示:
分数线不仅起着除号的作用,还起着括号的作用.去分母时,如果忽略分数线的括号作用,可能导致某些项的符号错误.因此,去分母时要注意添加括号.
5
易错点
因疏忽而漏解
防错警示:
6
易错点
列不等式组时,忽略隐含条件
例:某校计划将一批图书分给数学兴趣小组的同学,若每名同学分得5本,则
还余2本;若每名同学分得6本,则最后一名同学分得的图书少于2本.求兴
趣小组同学的人数和图书的本数.
解:设兴趣小组的同学有x人,则图书共有(5x+2)本.
根据题意,得0≤(5x+2)-6(x-1)<2,
解得6因为x为整数,所以x=7或x=8.
当x=7时,5x+2=37;
当x=8时,5x+2=42.
答:当兴趣小组的同学有7人时,图书共有37本;
当兴趣小组的同学有8人时,图书共有42本.
防错警示:
本题易出现将不等式组列为(5x+2)-6(x-1)<2的错误.本题中“最后一名同学分得的图书少于2本”包含两层含义,即最后一名同学分得的图书本数小于2,且大于等于0.出错的原因就是忽略了大于等于0这一隐含条件.
三、专题整合
1
专题
不等式性质的应用
不等式的性质不仅是不等式变形的重要依据,还是解不等式(组)的基础.
因此,掌握和灵活运用不等式的性质显得尤为重要.要特别注意不等式的基本性
质3,在不等式的两边都乘(或除以)同一个负数时,一定要改变不等号的方向.
解析:不等式的两边加(或减)同一个数(或式子),不等号的方向不变,所以A,C项
正确;不等号的两边乘(或除以)同一个正数,不等号的方向不变,所以B项正确;
不等式的两边乘(或除以)同一个负数,不等号的方向改变,所以D项错误.故选D.
警示:
应用不等式的性质解题时的两点注意
(1)当不等式两边乘(或除以)同一个负数时,不等号的方向要改变;
(2)挖掘不等式中的隐含条件,如由am2>bm2得到a>b,其中的隐含条件是m≠0.
2
专题
一元一次不等式(组)的解法
一元一次不等式(组)的解法是初中数学的重要内容之一.它是在解一元一次方程的基础上的延伸,由相等关系转化为了不等关系,其解法和步骤与解一元一次方程有相同点,但也有不同点.
反思:
本题考查的是一元一次不等式的解法,是中考中的常规题,过程与解一元一次方程类似.
方法:
解一元一次不等式组的关键是掌握确定各不等式解集公共部分的规律:同大取大,同小取小,大小小大中间找,大大小小无处找.
3
专题
求不等式(组)中字母参数的值或取值范围
由已知不等式(组)的解集或特殊解来确定字母参数的值或取值范围,常用的求解方法是先用解不等式(组)的方法求出含字母参数的不等式(组)的解集,再代入已给出的条件中,即可求出字母参数的值或取值范围.
技巧:
本题是有关不等式组的整数解问题的逆向运用,即已知不等式组的整数解的个数求字母参数的取值范围的问题.解答本题可以借助数轴,并注意对-4,-5的取舍.
4
专题
一元一次不等式(组)的实际应用
列一元一次不等式(组)解决实际问题,其关键是寻找题目中的不等关系.题目中给出的不等关系可分为两类:一是题目中的关键词语,如“大于”“小于”“至多”“至少”“超过”“不超过”等,直接根据关键词语表示不等关系;二是没有明显的关键词语,要在充分理解题意的基础上,提炼出具有不等关系的量,列出不等关系.
例:为支援灾区,某市民政局组织募捐了240吨救灾物资,现准备租用甲、乙两种货车,将这批救灾物资一次性全部运往灾区,它们的载质量和租金如下表:
车型
甲种货车
乙种货车
载质量(吨/辆)
45
30
租金(元/辆)
400
300
如果计划租用6辆货车,且租车的总费用不超过2300元,求最省钱的租车方案.
分析:不等关系有两种:货车的总载质量≥240吨,租车总费用≤2300.
4
专题
一元一次不等式(组)的实际应用
反思:
在利用不等式(组)解集实际问题时,要善于结合日常生活经验,从题目中寻找不等关系.另外,求不等式(组)的整数解是解决方案设计题最常用的方法之一.
四、思想方法
1
专题
数形结合思想
所谓数形结合就是在研究问题时,把数和形结合起来考虑.在本章解不等式组时,通常将各不等式的解集在数轴上表示出来,从而直观、快捷地得到不等式组的解集情况,也可逆用不等式组的解集,确定参数的取值或取值范围.
方法:A
数形结合思想是一种重要的数学思想方法,本题借助于数轴将不等式组的解集直观地表示出来,即可快捷地求出a的取值范围.
2
专题
分类讨论思想
有时要研究的问题的条件或结论中可能存在多种情况,为了准确求出问题的结果,我们在解题时要对条件或结论中存在的多种情况一一进行讨论,保证解答的严密性.分类讨论的关键是要做到不重不漏.
反思:
当问题存在多种不同情况时,要注意加以分类讨论,否则易因考虑不全面而出错.
第九章
不等式与不等式组
复习课
人教版数学七下
2020.6.10
by
wyj
学习目标
学习目标
1.熟记不等式的基本性质.
2.能熟练地解一元一次不等式和一元一次不等式组,并会运用一元一次不等式的知识解决实际问题.
3.通过解一元一次不等式(组),学会数形结合、分类讨论等数学思想.
重点
一元一次不等式(组)的解法
一、知识梳理
核心梳理
1.使不等式成立的
叫做不等式的解;不等式的
组成这个不等式的解集.
未知数的值
一个未知数
2.一元一次不等式:只含有
,并且未知数的最高次数是
.
所有的解
1
二、知识梳理
3.不等式的性质:
同一个数(或式子)
性质1:不等式两边都加(或减)
,不等号的方向
;
性质2:不等式的两边都乘(或除以)
,不等号的方向______.
性质3:不等式的两边都乘(或除以)
,不等号的方向______.?
同一个正数
同一个负数
不变
不变
改变
一、知识梳理
4.解一元一次不等式的一般步骤为:
(1)
(运用不等式的性质3,注意不要
),
漏乘不含分母的项
去分母
去括号
(2)
,
移项
合并同类项
相反数
(3)
(运用不等式的性质1,注意:被移的项要变为原来的
),
(4)
,
(5)
(运用不等式的性质2、3,注意何时需要改变不等号方向),
系数化为1
(6)把解集表示在数轴上.(注意:空心、实心小圆圈的区别;“>”“≥”向右拐,“<”“≤”向左拐)
5.解一元一次不等式组的步骤:
(1)
;
求出不等式组中每个不等式的解集
借助数轴找出各解集的公共部分
(2)
;
(3)
;
写出不等式组的解集
6.不等式组解集的确定方法,可以归纳为以下四种类型:(设a>b)
x
不等式组
图示
解集
(同大取___)
______
(同小取__)
_________(大小小大________)
大大小小________
大
小
中间找
找不到
7.列一元一次不等式解应用题的一般步骤:
(1)审题;
(2)
;
设未知数
找不等关系
(3)
,列不等式
(4)
;
解不等式
(5)检验并作答.
活动:下列式子中,一元一次不等式有(
)
①3x-1≥4
②
2+3x>6
③
3-
<5
④
⑤
⑥
x+xy≥y2
⑦x>0
A.5个
B.4个
C.6个
D.3个
A
√
√
×
√
√
×
√
探究一:不等式及其相关概念
二、知识应用
【归纳总结】一元一次不等式的概念含几个要点:
(3)只含有一个未知数,且含有未知数的项的最高次数为1.
(2)不等号两边都是关于未知数的整式;
(1)用不等号连接;
探究二:解不等式(组)
活动1:解不等式:x+
>1-
.
解:去分母,得8x+3(x+1)>8-4(x-5),
去括号,得8x+3x+3>8-4x+20,
移项、合并同类项,得15x>25,
系数化为1,得x>
.
解:由
①
得:x
>
–
1
;
活动2:解不等式组
,并把解集表示在数轴上.
①②
由
②
得:x
<
3;
–
1
0
1
2
3
4
数轴表示:
不等式组的解集是
–1
<
x
<
3
探究三:列不等式解应用题
活动:春运期间,某汽车站设有6个检票口,假设有120名乘客要上车,启用3个检票口,4分钟全部检查完.假若有180名乘客要上车,要在5分钟内全部检查完,则至少得启用几个检票口?
解:
要启用x个检票口,根据题意,得:
因为x取整数,所以x=4.
故至少启用4个检票口.
x>
,解得x>3.6.
D
3.某品牌电脑的成本价为2400元,售价为2800元,该商店准备举行打折促销
活动,要求利润率不低于5%,如果将这种品牌的电脑打x折销售,则下列不
等式中能正确表示该商店的促销方式的是( )
A.2800x≥2400×5%
B.2800x﹣2400≥2400×5%
C.2800×
≥2400×5%
D.2800×
﹣2400≥2400×5%
4.一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数.
解:
设小朋友总共有x人,由此可得不等式组
3x+4-4(x-1)≥0,
3x+4-4(x-1)<3;
解得5
所以有三种可能:
因为x是整数,
①小朋友有6人,玩具有22件;
②小朋友有7人,玩具有25件;
③小朋友有8人,玩具有28件
二、易错点辨析
1
易错点
不等式变形后忘记改变不等号的方向
防错警示:
本题的易错点为在应用不等式的性质3将不等式变形时,忘记改变不等号的方向.
2
易错点
忽略不等式中字母取0的特殊情况
防错警示:
3
易错点
去分母时漏乘常数项
防错警示:
去分母时,不等式的两边的各项都应乘各分泌的最小公倍数,不要漏乘常数项.
4
易错点
去分母时忽略分数线的括号作用
防错警示:
分数线不仅起着除号的作用,还起着括号的作用.去分母时,如果忽略分数线的括号作用,可能导致某些项的符号错误.因此,去分母时要注意添加括号.
5
易错点
因疏忽而漏解
防错警示:
6
易错点
列不等式组时,忽略隐含条件
例:某校计划将一批图书分给数学兴趣小组的同学,若每名同学分得5本,则
还余2本;若每名同学分得6本,则最后一名同学分得的图书少于2本.求兴
趣小组同学的人数和图书的本数.
解:设兴趣小组的同学有x人,则图书共有(5x+2)本.
根据题意,得0≤(5x+2)-6(x-1)<2,
解得6
当x=7时,5x+2=37;
当x=8时,5x+2=42.
答:当兴趣小组的同学有7人时,图书共有37本;
当兴趣小组的同学有8人时,图书共有42本.
防错警示:
本题易出现将不等式组列为(5x+2)-6(x-1)<2的错误.本题中“最后一名同学分得的图书少于2本”包含两层含义,即最后一名同学分得的图书本数小于2,且大于等于0.出错的原因就是忽略了大于等于0这一隐含条件.
三、专题整合
1
专题
不等式性质的应用
不等式的性质不仅是不等式变形的重要依据,还是解不等式(组)的基础.
因此,掌握和灵活运用不等式的性质显得尤为重要.要特别注意不等式的基本性
质3,在不等式的两边都乘(或除以)同一个负数时,一定要改变不等号的方向.
解析:不等式的两边加(或减)同一个数(或式子),不等号的方向不变,所以A,C项
正确;不等号的两边乘(或除以)同一个正数,不等号的方向不变,所以B项正确;
不等式的两边乘(或除以)同一个负数,不等号的方向改变,所以D项错误.故选D.
警示:
应用不等式的性质解题时的两点注意
(1)当不等式两边乘(或除以)同一个负数时,不等号的方向要改变;
(2)挖掘不等式中的隐含条件,如由am2>bm2得到a>b,其中的隐含条件是m≠0.
2
专题
一元一次不等式(组)的解法
一元一次不等式(组)的解法是初中数学的重要内容之一.它是在解一元一次方程的基础上的延伸,由相等关系转化为了不等关系,其解法和步骤与解一元一次方程有相同点,但也有不同点.
反思:
本题考查的是一元一次不等式的解法,是中考中的常规题,过程与解一元一次方程类似.
方法:
解一元一次不等式组的关键是掌握确定各不等式解集公共部分的规律:同大取大,同小取小,大小小大中间找,大大小小无处找.
3
专题
求不等式(组)中字母参数的值或取值范围
由已知不等式(组)的解集或特殊解来确定字母参数的值或取值范围,常用的求解方法是先用解不等式(组)的方法求出含字母参数的不等式(组)的解集,再代入已给出的条件中,即可求出字母参数的值或取值范围.
技巧:
本题是有关不等式组的整数解问题的逆向运用,即已知不等式组的整数解的个数求字母参数的取值范围的问题.解答本题可以借助数轴,并注意对-4,-5的取舍.
4
专题
一元一次不等式(组)的实际应用
列一元一次不等式(组)解决实际问题,其关键是寻找题目中的不等关系.题目中给出的不等关系可分为两类:一是题目中的关键词语,如“大于”“小于”“至多”“至少”“超过”“不超过”等,直接根据关键词语表示不等关系;二是没有明显的关键词语,要在充分理解题意的基础上,提炼出具有不等关系的量,列出不等关系.
例:为支援灾区,某市民政局组织募捐了240吨救灾物资,现准备租用甲、乙两种货车,将这批救灾物资一次性全部运往灾区,它们的载质量和租金如下表:
车型
甲种货车
乙种货车
载质量(吨/辆)
45
30
租金(元/辆)
400
300
如果计划租用6辆货车,且租车的总费用不超过2300元,求最省钱的租车方案.
分析:不等关系有两种:货车的总载质量≥240吨,租车总费用≤2300.
4
专题
一元一次不等式(组)的实际应用
反思:
在利用不等式(组)解集实际问题时,要善于结合日常生活经验,从题目中寻找不等关系.另外,求不等式(组)的整数解是解决方案设计题最常用的方法之一.
四、思想方法
1
专题
数形结合思想
所谓数形结合就是在研究问题时,把数和形结合起来考虑.在本章解不等式组时,通常将各不等式的解集在数轴上表示出来,从而直观、快捷地得到不等式组的解集情况,也可逆用不等式组的解集,确定参数的取值或取值范围.
方法:A
数形结合思想是一种重要的数学思想方法,本题借助于数轴将不等式组的解集直观地表示出来,即可快捷地求出a的取值范围.
2
专题
分类讨论思想
有时要研究的问题的条件或结论中可能存在多种情况,为了准确求出问题的结果,我们在解题时要对条件或结论中存在的多种情况一一进行讨论,保证解答的严密性.分类讨论的关键是要做到不重不漏.
反思:
当问题存在多种不同情况时,要注意加以分类讨论,否则易因考虑不全面而出错.
