华师大版八年级下数学19.2.2菱形的判定经典课件(35张)
文档属性
| 名称 | 华师大版八年级下数学19.2.2菱形的判定经典课件(35张) |  | |
| 格式 | zip | ||
| 文件大小 | 623.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 23:23:45 | ||
图片预览









文档简介
(共35张PPT)
§19.2
.2
菱形的判定
菱形
学习目标
1.理解并掌握菱形的判定方法.
2.能应用菱形的判定方法解决简单的证明题和计算题.
复习与回顾:
1.菱形的定义:
2.菱形的性质:
有一组邻边相等的平行四边形叫做菱形。
?
?
对边平行
四边相等
对角相等
对角线互相平分、互相垂直且平分每一组对角
菱形性质
边
角
对角线
邻角互补
复习巩固
1、菱形的两条对角线长分别是6cm和8cm,则菱形
的周长
,面积
。
2、菱形的面积为24cm2,一条对角线的长为6cm,则另一条对角线长为
;边长为
。
3、已知菱形的两个邻角的比是1:5,高是
8cm,则菱形的周长为
。
4、已知菱形的周长为40cm,两对角线的比为3:4,则两对角线的长分别是
。
变式题
(1)菱形两条对角线长为6和8,菱形的边长
为
,面积为
。
(2)菱形ABCD的面积为96,对角线AC长
为16
,此菱形的边长为
。
(3)菱形对角线的平方和等于一边平方的___
(
)
A.
2倍
B.
3倍
C.4倍
D.
5倍
5
4
10
C
变式题
(1)菱形两条对角线长为6和8,菱形的边长
为
,面积为
。
(2)菱形ABCD的面积为96,对角线AC长
为16
,此菱形的边长为
。
(3)菱形对角线的平方和等于一边平方的___
(
)
A.
2倍
B.
3倍
C.4倍
D.
5倍
5
4
10
C
A
B
C
D
E
F
变式题(1):菱形ABCD
,E、F分别ABCD的中点,求证:CE=CF.
(2)如果上题中还有CE⊥AB,
CF⊥AD,求各内角的度数
A
B
C
E
F
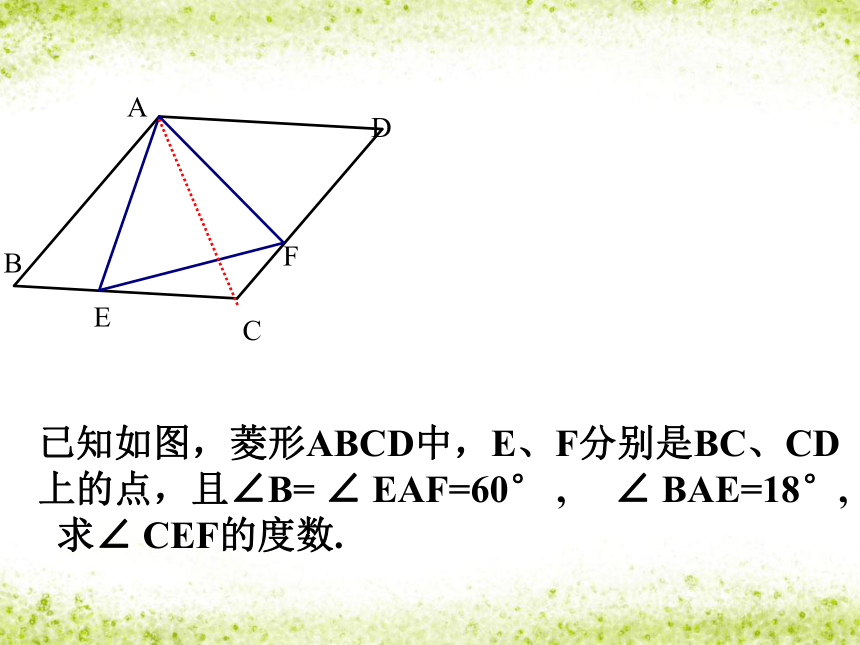
已知如图,菱形ABCD中,E、F分别是BC、CD
上的点,且∠B=
∠
EAF=60°
,
∠
BAE=18°,
求∠
CEF的度数.
D
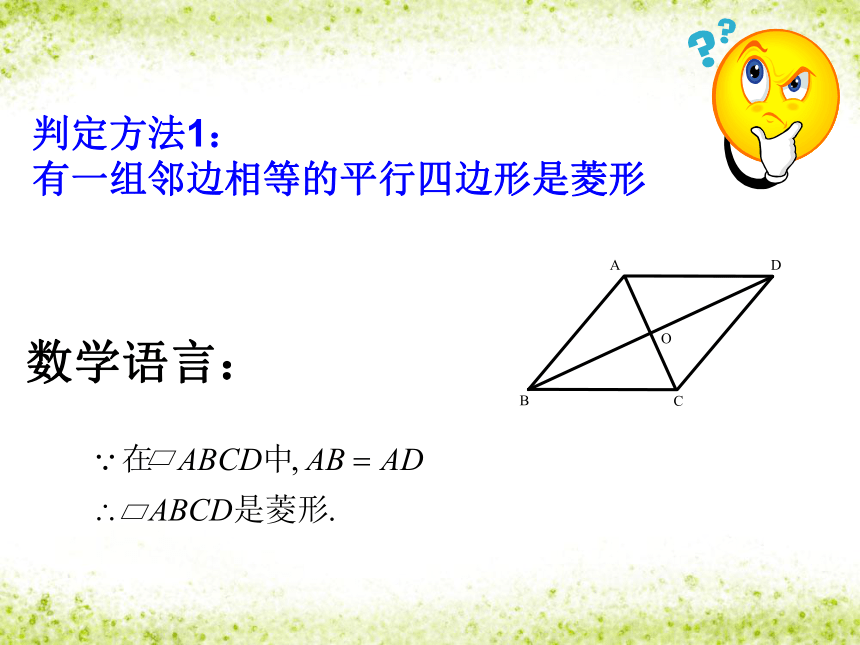
数学语言:
判定方法1:
有一组邻边相等的平行四边形是菱形
想一想
如果一个四边形是平行四边形,则只要再有什么条件就可以判定它是一个菱形?根据什么?
有一组邻边相等的平行四边形叫做菱形.
根据定义得:
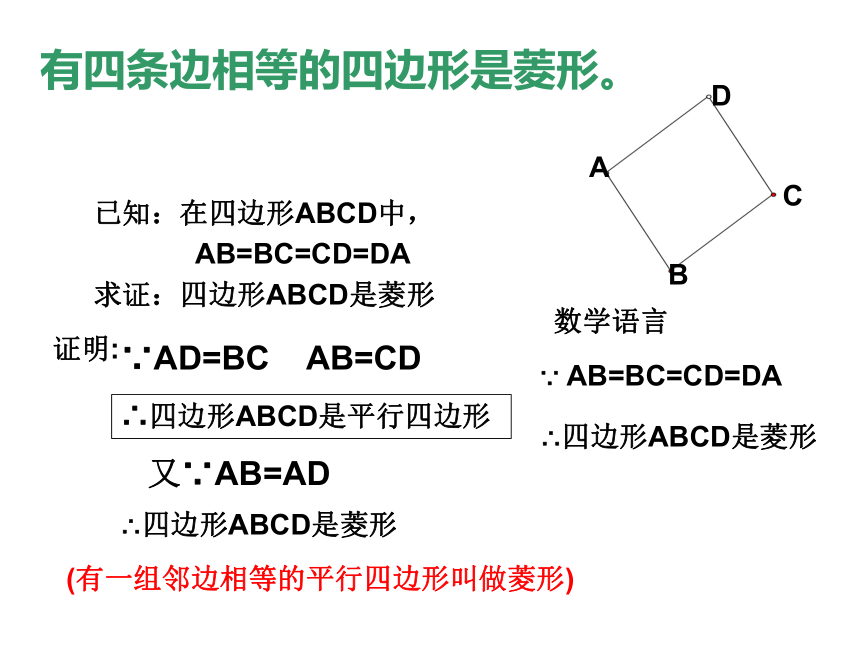
有四条边相等的四边形是菱形。
数学语言
∴四边形ABCD是平行四边形
已知:在四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形
证明:
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵
AB=BC=CD=DA
∴四边形ABCD是菱形
∵AD=BC
AB=CD
又∵AB=AD
对角线互相垂直的平行四边形是菱形.
证明:
∴
ABCD是菱形
又∵
AC
⊥
BD;
∵四边形ABCD是平行四边形
∴OA=OC
∴BA=BC
数学语言
∵四边形ABCD是平行四边形;
AC
⊥
BD;
∴
□
ABCD是菱形
O
(线段垂直平分线上的点到线段两个端点的距离相等)
(有一组邻边相等的
平行四边形叫做菱形).
归纳
菱形常用的判定方法:
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有四条边相等的四边形是菱形.
菱形的判定:
∵AB=BC=CD=DA
∴□ABCD是菱形
∵
AC⊥BD
∴□ABCD
是菱形
AB=AD
∴四边形ABCD是菱形
一组邻边相等的平行四边形是菱形
文字语言
图形语言
符号语言
判定法一
∵
判定
法二
四边相等的四边形是菱形
判定法三
对角线互相垂直的平行四边形是菱形
1、下列三个图形是不是菱形,为什么?
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
2、判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(
)
(2)对角线互相垂直平分的四边形是菱形;(
)
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(
)
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
(
)
╳
√
╳
╳
3、□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是
形;
(2)若AC=BD,则□ABCD是
形;
(3)若∠ABC是直角,则□ABCD是
形;
(4)若∠BAO=∠DAO,则□ABCD是
形。
矩
菱
矩
菱
做一做:判断下列命题是否正确,并说明理由.
(1)对角线互相平分且邻边相等的四边形是菱形.
(2)两组对边分别平行且一组邻边相等的四边形
是菱形.
(3)邻角相等的四边形是菱形.
(4)有一组邻边相等的四边形是菱形.
(5)两组对角分别相等且对角线互相垂直的四边形
。
(8)一条对角线平分一个内角的平行四边形是菱形。
(1).下列命题中正确的是(
)
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
(2).对角线互相垂直且平分的四边形是(
)
A.矩形
B.一般的平行四边形
C.菱形
D.以上都不对
C
(3).下列条件中,不能判定四边形ABCD为菱形的是(
)
A.AC⊥BD,AC与BD互相平分
B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD
D.AB=CD,AD=BC,AC⊥BD
C
4、选择:
24㎝?
菱形
=
=
如图,
ABCD的两条对角线AC、BD相交于点O,AB=
5
,AC=8,DB=6
求证:四边形ABCD是菱形.
∴四边形ABCD是菱形.
∴OA=OC=4
OB=OD=3
证明:
∵
AB=5
∴AC⊥BD
∴
∠AOB=
(1)∵
四边形ABCD是平行四边形
(平行四边形的对角线互相平分)
(对角线互相垂直的平行四边形是菱形).
例题1
例题2
已知:
ABCD的对角线AC的垂直平分线与边AD
、BC分别交于E、F
求证:四边形AFCE是菱形。
分析:
(1)利用定义判定
(2)
由已知可知
OA=OC,EF⊥AC.
(3)利用四边相等,你会吗?
分析:
四边形AFCE是菱形
AE=EC=CF=FA
AE=EC
AF=CF
AE=AF
EF
垂直平分AC
∠1=
∠2
∠1=
∠3
∠2=
∠3
AE∥FC
四边形ABCD
是平行四边形
AF=CF
EF
⊥AC
1
2
3
8、已知:如图,AD平分∠BAC,DE∥AC
交AB于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形.
∴
□AEDF是菱形
证明:∵DE∥AC
DF∥AB
∴四边形AEDF是平行四边形
∵
DE∥AC
∴∠2=∠3
∵
AD是△ABC的角平分线
∴
∠1=∠2
∴AE=DE
∴
∠1=∠3
如图,AD∥BC,BD垂直平分AC,四边形ABCD一定是菱形吗?若是,请说明理由。
思考题:
┐
)
1
2
(
∟
∟
E
F
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
思考:
请你动脑筋
1、如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,说明CE⊥DF.
2.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE
∥BD.
求证:四边形OCED是菱形
3.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于点E,连接AE、CD.
求证:四边形ADCE是菱形
B
C
N
4、如图,Rt△ABC中,∠ACB=900,∠BAC=600,DE垂直平分BC,垂足为D,交AB于E,又点F在DE的延长线上,且AF=CE,求证:四边形ACEF是菱形。
7、已知如图,AD是的角平分线,DE∥AC,DF∥AB.
求证:四边形AEDF是菱形。
对于这道,小林是这样证明的。
证明:∵AD平分∠EAF,
∴∠1=∠2,
∵DE∥AC,∴∠2=∠3
∵DF∥AB,∴∠1=∠4
又有AD=AD,∴△AED≌△AFD.
∴AE=AF,DE=DF.
∴四边形AEDF是菱形.
老师说小林的解题过程有错误,你能看出来吗?
⑴请你帮小林指出他的错误是什么?(先在解答过程中划出来,再说明他错误的原因)
⑵请你帮小林做出正确的解答。
如图在△ABC中,∠BAC=90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于C,EF⊥BC于F,四边形AEFG是菱形吗?
探究释疑
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
小结:
矩形与菱形
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
平行四边形的性质
性质
边
角
对角线
四个角都是直角
相等
互相垂直且平分每一组对角
判定
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
有一组邻边相等的平行四边形
对角线互相垂直的平行四边形
四条边都相等的四边形
四条边都相等
矩形
菱形
定义
§19.2
.2
菱形的判定
菱形
学习目标
1.理解并掌握菱形的判定方法.
2.能应用菱形的判定方法解决简单的证明题和计算题.
复习与回顾:
1.菱形的定义:
2.菱形的性质:
有一组邻边相等的平行四边形叫做菱形。
?
?
对边平行
四边相等
对角相等
对角线互相平分、互相垂直且平分每一组对角
菱形性质
边
角
对角线
邻角互补
复习巩固
1、菱形的两条对角线长分别是6cm和8cm,则菱形
的周长
,面积
。
2、菱形的面积为24cm2,一条对角线的长为6cm,则另一条对角线长为
;边长为
。
3、已知菱形的两个邻角的比是1:5,高是
8cm,则菱形的周长为
。
4、已知菱形的周长为40cm,两对角线的比为3:4,则两对角线的长分别是
。
变式题
(1)菱形两条对角线长为6和8,菱形的边长
为
,面积为
。
(2)菱形ABCD的面积为96,对角线AC长
为16
,此菱形的边长为
。
(3)菱形对角线的平方和等于一边平方的___
(
)
A.
2倍
B.
3倍
C.4倍
D.
5倍
5
4
10
C
变式题
(1)菱形两条对角线长为6和8,菱形的边长
为
,面积为
。
(2)菱形ABCD的面积为96,对角线AC长
为16
,此菱形的边长为
。
(3)菱形对角线的平方和等于一边平方的___
(
)
A.
2倍
B.
3倍
C.4倍
D.
5倍
5
4
10
C
A
B
C
D
E
F
变式题(1):菱形ABCD
,E、F分别ABCD的中点,求证:CE=CF.
(2)如果上题中还有CE⊥AB,
CF⊥AD,求各内角的度数
A
B
C
E
F
已知如图,菱形ABCD中,E、F分别是BC、CD
上的点,且∠B=
∠
EAF=60°
,
∠
BAE=18°,
求∠
CEF的度数.
D
数学语言:
判定方法1:
有一组邻边相等的平行四边形是菱形
想一想
如果一个四边形是平行四边形,则只要再有什么条件就可以判定它是一个菱形?根据什么?
有一组邻边相等的平行四边形叫做菱形.
根据定义得:
有四条边相等的四边形是菱形。
数学语言
∴四边形ABCD是平行四边形
已知:在四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形
证明:
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵
AB=BC=CD=DA
∴四边形ABCD是菱形
∵AD=BC
AB=CD
又∵AB=AD
对角线互相垂直的平行四边形是菱形.
证明:
∴
ABCD是菱形
又∵
AC
⊥
BD;
∵四边形ABCD是平行四边形
∴OA=OC
∴BA=BC
数学语言
∵四边形ABCD是平行四边形;
AC
⊥
BD;
∴
□
ABCD是菱形
O
(线段垂直平分线上的点到线段两个端点的距离相等)
(有一组邻边相等的
平行四边形叫做菱形).
归纳
菱形常用的判定方法:
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有四条边相等的四边形是菱形.
菱形的判定:
∵AB=BC=CD=DA
∴□ABCD是菱形
∵
AC⊥BD
∴□ABCD
是菱形
AB=AD
∴四边形ABCD是菱形
一组邻边相等的平行四边形是菱形
文字语言
图形语言
符号语言
判定法一
∵
判定
法二
四边相等的四边形是菱形
判定法三
对角线互相垂直的平行四边形是菱形
1、下列三个图形是不是菱形,为什么?
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
2、判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(
)
(2)对角线互相垂直平分的四边形是菱形;(
)
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(
)
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
(
)
╳
√
╳
╳
3、□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是
形;
(2)若AC=BD,则□ABCD是
形;
(3)若∠ABC是直角,则□ABCD是
形;
(4)若∠BAO=∠DAO,则□ABCD是
形。
矩
菱
矩
菱
做一做:判断下列命题是否正确,并说明理由.
(1)对角线互相平分且邻边相等的四边形是菱形.
(2)两组对边分别平行且一组邻边相等的四边形
是菱形.
(3)邻角相等的四边形是菱形.
(4)有一组邻边相等的四边形是菱形.
(5)两组对角分别相等且对角线互相垂直的四边形
。
(8)一条对角线平分一个内角的平行四边形是菱形。
(1).下列命题中正确的是(
)
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
(2).对角线互相垂直且平分的四边形是(
)
A.矩形
B.一般的平行四边形
C.菱形
D.以上都不对
C
(3).下列条件中,不能判定四边形ABCD为菱形的是(
)
A.AC⊥BD,AC与BD互相平分
B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD
D.AB=CD,AD=BC,AC⊥BD
C
4、选择:
24㎝?
菱形
=
=
如图,
ABCD的两条对角线AC、BD相交于点O,AB=
5
,AC=8,DB=6
求证:四边形ABCD是菱形.
∴四边形ABCD是菱形.
∴OA=OC=4
OB=OD=3
证明:
∵
AB=5
∴AC⊥BD
∴
∠AOB=
(1)∵
四边形ABCD是平行四边形
(平行四边形的对角线互相平分)
(对角线互相垂直的平行四边形是菱形).
例题1
例题2
已知:
ABCD的对角线AC的垂直平分线与边AD
、BC分别交于E、F
求证:四边形AFCE是菱形。
分析:
(1)利用定义判定
(2)
由已知可知
OA=OC,EF⊥AC.
(3)利用四边相等,你会吗?
分析:
四边形AFCE是菱形
AE=EC=CF=FA
AE=EC
AF=CF
AE=AF
EF
垂直平分AC
∠1=
∠2
∠1=
∠3
∠2=
∠3
AE∥FC
四边形ABCD
是平行四边形
AF=CF
EF
⊥AC
1
2
3
8、已知:如图,AD平分∠BAC,DE∥AC
交AB于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形.
∴
□AEDF是菱形
证明:∵DE∥AC
DF∥AB
∴四边形AEDF是平行四边形
∵
DE∥AC
∴∠2=∠3
∵
AD是△ABC的角平分线
∴
∠1=∠2
∴AE=DE
∴
∠1=∠3
如图,AD∥BC,BD垂直平分AC,四边形ABCD一定是菱形吗?若是,请说明理由。
思考题:
┐
)
1
2
(
∟
∟
E
F
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
思考:
请你动脑筋
1、如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,说明CE⊥DF.
2.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE
∥BD.
求证:四边形OCED是菱形
3.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于点E,连接AE、CD.
求证:四边形ADCE是菱形
B
C
N
4、如图,Rt△ABC中,∠ACB=900,∠BAC=600,DE垂直平分BC,垂足为D,交AB于E,又点F在DE的延长线上,且AF=CE,求证:四边形ACEF是菱形。
7、已知如图,AD是的角平分线,DE∥AC,DF∥AB.
求证:四边形AEDF是菱形。
对于这道,小林是这样证明的。
证明:∵AD平分∠EAF,
∴∠1=∠2,
∵DE∥AC,∴∠2=∠3
∵DF∥AB,∴∠1=∠4
又有AD=AD,∴△AED≌△AFD.
∴AE=AF,DE=DF.
∴四边形AEDF是菱形.
老师说小林的解题过程有错误,你能看出来吗?
⑴请你帮小林指出他的错误是什么?(先在解答过程中划出来,再说明他错误的原因)
⑵请你帮小林做出正确的解答。
如图在△ABC中,∠BAC=90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于C,EF⊥BC于F,四边形AEFG是菱形吗?
探究释疑
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
小结:
矩形与菱形
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
平行四边形的性质
性质
边
角
对角线
四个角都是直角
相等
互相垂直且平分每一组对角
判定
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
有一组邻边相等的平行四边形
对角线互相垂直的平行四边形
四条边都相等的四边形
四条边都相等
矩形
菱形
定义
