华师大版八年级下数学19.2.1菱形的性质与判定课件(24张ppt)
文档属性
| 名称 | 华师大版八年级下数学19.2.1菱形的性质与判定课件(24张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 292.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-12 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
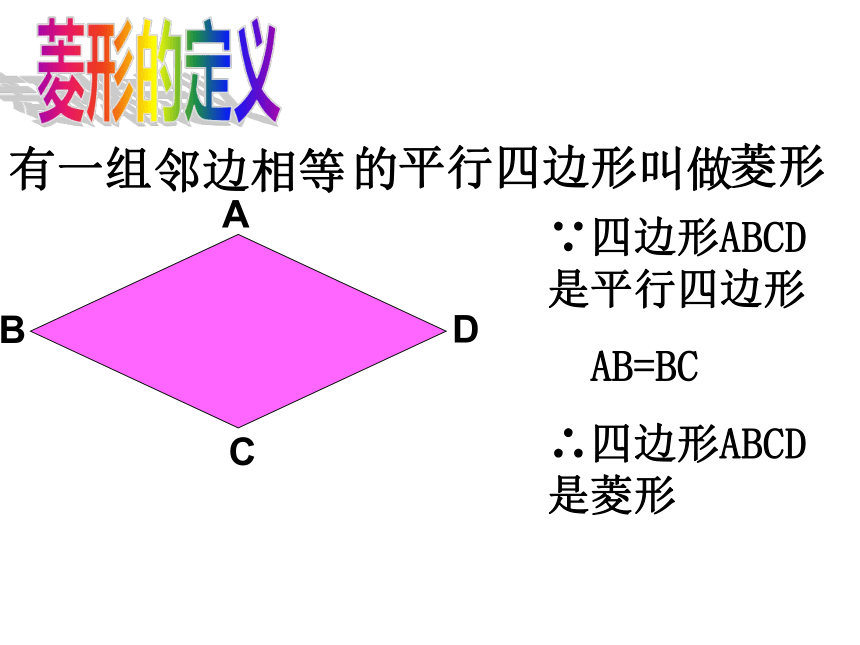
在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
平行四边形
菱形
菱形的性质与判定
有一组
的
叫做
邻边相等
平行四边形
A
D
C
B
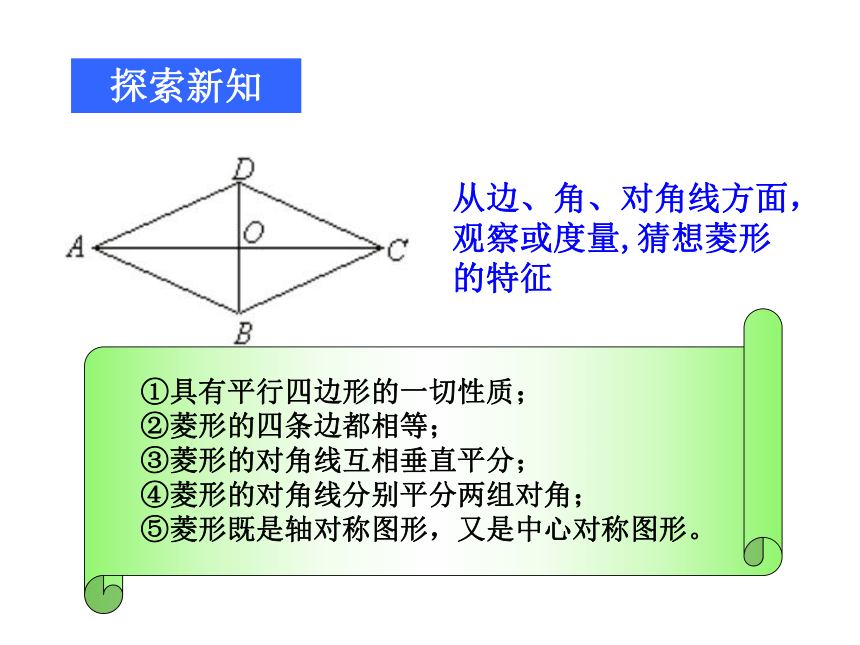
∵四边形ABCD是平行四边形
AB=BC
∴四边形ABCD是菱形
菱形
从边、角、对角线方面,观察或度量,猜想菱形的特征
①具有平行四边形的一切性质;
②菱形的四条边都相等;
③菱形的对角线互相垂直平分;
④菱形的对角线分别平分两组对角;
⑤菱形既是轴对称图形,又是中心对称图形。
探索新知
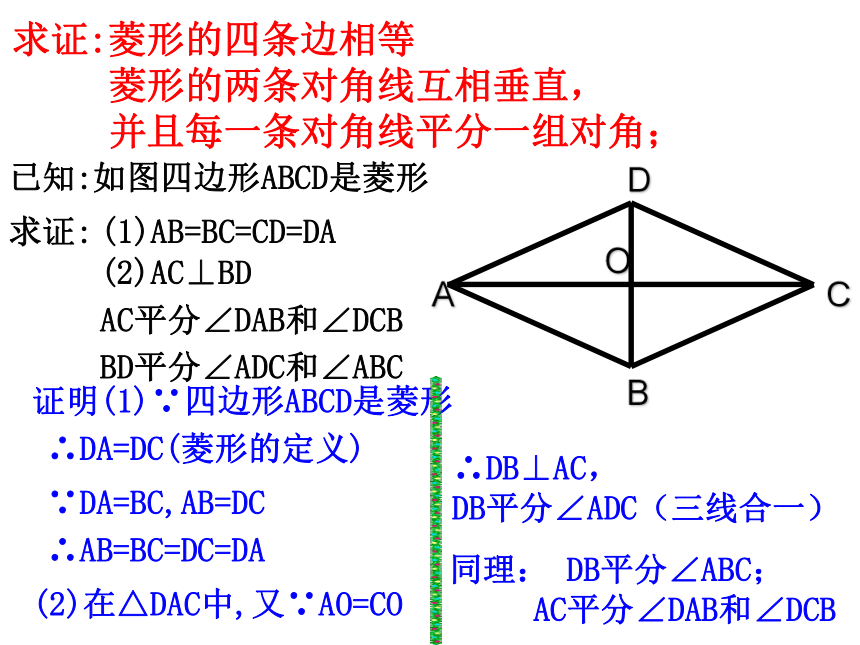
已知:如图四边形ABCD是菱形
求证:菱形的四条边相等
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;
证明(1)∵四边形ABCD是菱形
∴DA=DC(菱形的定义)
∵DA=BC,AB=DC
∴AB=BC=DC=DA
(2)在△DAC中,又∵AO=CO
∴DB⊥AC,
DB平分∠ADC(三线合一)
同理:
DB平分∠ABC;
AC平分∠DAB和∠DCB
(1)AB=BC=CD=DA
(2)AC⊥BD
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC
求证:
1.菱形具有而平行四边形不具有的性质是:( )
(A)对角线互相平分
(B)对角线相等
(C)对角线互相垂直且相等
(D)对角线互相垂直且每一条对角线平分一组对角
D
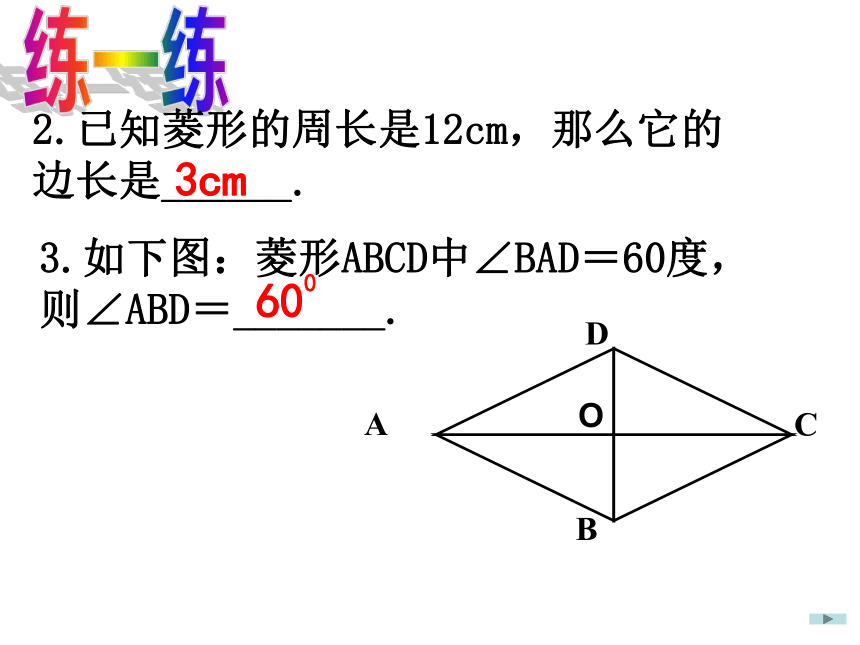
3cm
600
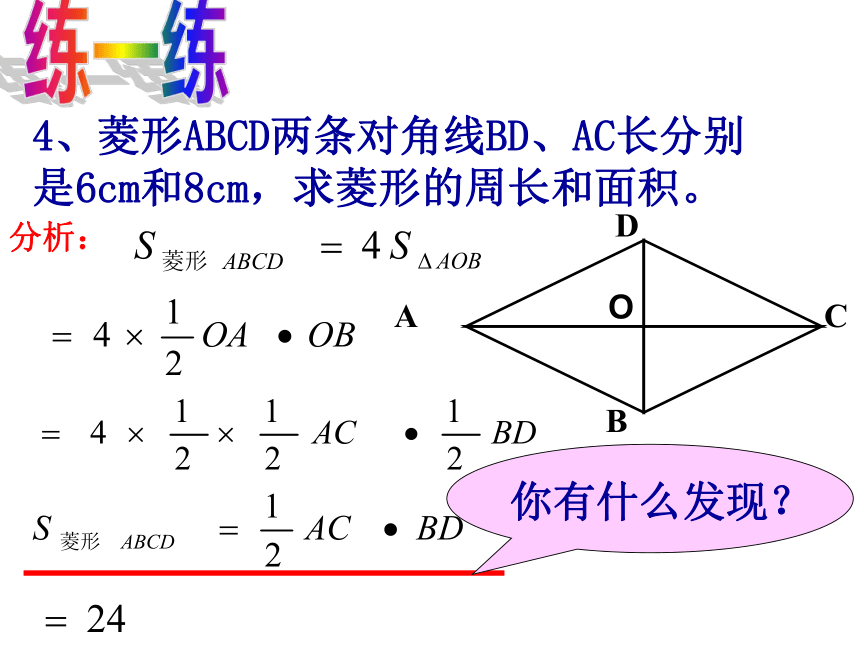
4、菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的周长和面积。
分析:
如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。
你敢挑战吗?
交流反思
1.菱形概念
2.菱形特征
3.菱形与平行四边形的关系
①具有平行四边形的一切性质;
②菱形的四条边都相等;
③菱形的对角线互相垂直平分;
④菱形的对角线分别平分两组对角;
⑤菱形既是轴对称图形,又是中心对称图形。
有一组邻边相等的平行四边形叫做菱形
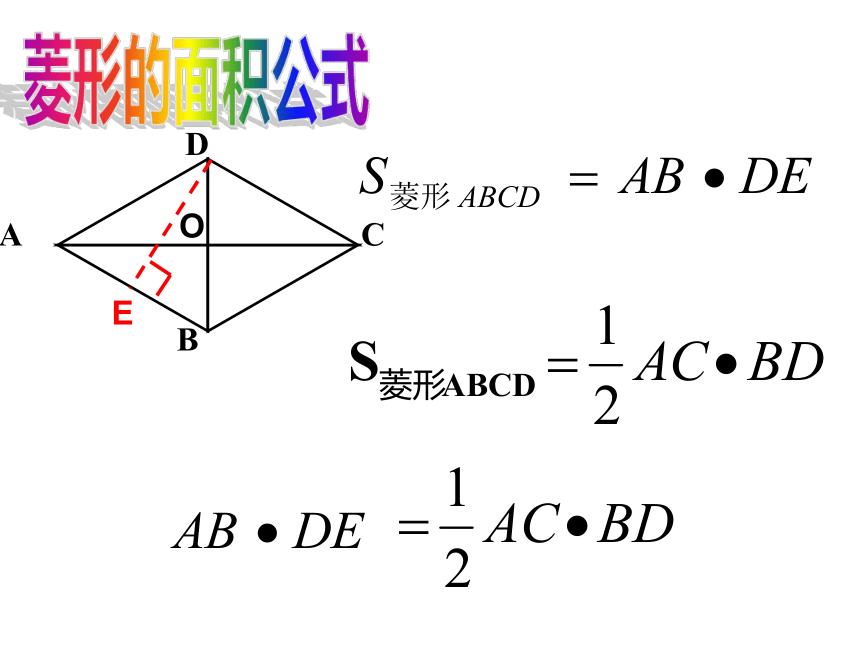
4.菱形的面积
=
对角线乘积的一半
菱形的判定
1.菱形判定方法1:用定义
有一组邻边相等的平行四边形叫做菱形。
平行四边形
符号语言:
∵四边形ABCD是
平行四边形
AB=AD
已知:在
ABCD
中,对角线AC⊥BD
求证:
ABCD是菱形。
证明:
∵四边形ABCD是平行四边形,
∴OB=OD
又∵AC⊥BD
∴AB=AD
菱形判定方法:
对角线互相垂直的平行四边形是菱形。
符号语言:
O
命题:有四条边相等的四边形是菱形。
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
∵AB=BC=CD=DA
∴四边形ABCD是菱形。
符号语言:
菱形的判定
观察与思考:如图,四边形ABCD的对角线AC⊥BD,则四边形ABCD是不是菱形?
注:
对角线互相垂直的四边形不能判定为菱形。
菱形的判定:
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵在□ABCD中
AC⊥BD
∴四边形ABCD是菱形
∵在□ABCD中
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
一组邻边相等的平行四边形是菱形
文字语言
图形语言
符号语言
判定法一
判定
法二
对角线互相垂直的平行四边形是菱形
判定法三
四边相等的四边形是菱形
方法总结:
四边形
平行四边形
一组邻边相等
对角线互相垂直
菱形
有四条边相等
菱形
判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(
)
(2)对角线互相垂直平分的四边形是菱形;(
)
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(
)
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
(
)
╳
√
╳
╳
□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是
形;
(2)若AC=BD,则□ABCD是
形;
(3)若∠ABC是直角,则□ABCD是
形;
(4)若∠BAO=∠DAO,则□ABCD是
形。
矩
菱
矩
菱
如图,矩形ABCD的对角线相交于点O,DE∥AC,AE∥DB,AE交DE于E。
求证:四边形AODE是菱形。
2、将两张宽度相等的矩形纸片叠放在一起得到如图所示的四边形ABCD.
求证:四边形ABCD是菱形。
M
N
3、如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别交于点E、F。四边形AFCE是菱形吗?为什么?
4、已知,如图,在△ABC中,AD是角平分线,
E是AB上一点,且AE=AC,EF∥BC,
EF交AD于点F.
求证:四边形CDEF是菱形。
在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
平行四边形
菱形
菱形的性质与判定
有一组
的
叫做
邻边相等
平行四边形
A
D
C
B
∵四边形ABCD是平行四边形
AB=BC
∴四边形ABCD是菱形
菱形
从边、角、对角线方面,观察或度量,猜想菱形的特征
①具有平行四边形的一切性质;
②菱形的四条边都相等;
③菱形的对角线互相垂直平分;
④菱形的对角线分别平分两组对角;
⑤菱形既是轴对称图形,又是中心对称图形。
探索新知
已知:如图四边形ABCD是菱形
求证:菱形的四条边相等
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;
证明(1)∵四边形ABCD是菱形
∴DA=DC(菱形的定义)
∵DA=BC,AB=DC
∴AB=BC=DC=DA
(2)在△DAC中,又∵AO=CO
∴DB⊥AC,
DB平分∠ADC(三线合一)
同理:
DB平分∠ABC;
AC平分∠DAB和∠DCB
(1)AB=BC=CD=DA
(2)AC⊥BD
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC
求证:
1.菱形具有而平行四边形不具有的性质是:( )
(A)对角线互相平分
(B)对角线相等
(C)对角线互相垂直且相等
(D)对角线互相垂直且每一条对角线平分一组对角
D
3cm
600
4、菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的周长和面积。
分析:
如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。
你敢挑战吗?
交流反思
1.菱形概念
2.菱形特征
3.菱形与平行四边形的关系
①具有平行四边形的一切性质;
②菱形的四条边都相等;
③菱形的对角线互相垂直平分;
④菱形的对角线分别平分两组对角;
⑤菱形既是轴对称图形,又是中心对称图形。
有一组邻边相等的平行四边形叫做菱形
4.菱形的面积
=
对角线乘积的一半
菱形的判定
1.菱形判定方法1:用定义
有一组邻边相等的平行四边形叫做菱形。
平行四边形
符号语言:
∵四边形ABCD是
平行四边形
AB=AD
已知:在
ABCD
中,对角线AC⊥BD
求证:
ABCD是菱形。
证明:
∵四边形ABCD是平行四边形,
∴OB=OD
又∵AC⊥BD
∴AB=AD
菱形判定方法:
对角线互相垂直的平行四边形是菱形。
符号语言:
O
命题:有四条边相等的四边形是菱形。
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
∵AB=BC=CD=DA
∴四边形ABCD是菱形。
符号语言:
菱形的判定
观察与思考:如图,四边形ABCD的对角线AC⊥BD,则四边形ABCD是不是菱形?
注:
对角线互相垂直的四边形不能判定为菱形。
菱形的判定:
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵在□ABCD中
AC⊥BD
∴四边形ABCD是菱形
∵在□ABCD中
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
一组邻边相等的平行四边形是菱形
文字语言
图形语言
符号语言
判定法一
判定
法二
对角线互相垂直的平行四边形是菱形
判定法三
四边相等的四边形是菱形
方法总结:
四边形
平行四边形
一组邻边相等
对角线互相垂直
菱形
有四条边相等
菱形
判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(
)
(2)对角线互相垂直平分的四边形是菱形;(
)
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(
)
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
(
)
╳
√
╳
╳
□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是
形;
(2)若AC=BD,则□ABCD是
形;
(3)若∠ABC是直角,则□ABCD是
形;
(4)若∠BAO=∠DAO,则□ABCD是
形。
矩
菱
矩
菱
如图,矩形ABCD的对角线相交于点O,DE∥AC,AE∥DB,AE交DE于E。
求证:四边形AODE是菱形。
2、将两张宽度相等的矩形纸片叠放在一起得到如图所示的四边形ABCD.
求证:四边形ABCD是菱形。
M
N
3、如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别交于点E、F。四边形AFCE是菱形吗?为什么?
4、已知,如图,在△ABC中,AD是角平分线,
E是AB上一点,且AE=AC,EF∥BC,
EF交AD于点F.
求证:四边形CDEF是菱形。
