华师大版八年级下数学19.1.2矩形的判定课件(19张ppt)
文档属性
| 名称 | 华师大版八年级下数学19.1.2矩形的判定课件(19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 612.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-12 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
19.1.2
矩形的判定
一个角是直角
有
的平行四边形叫做矩形
矩形
平行四边形
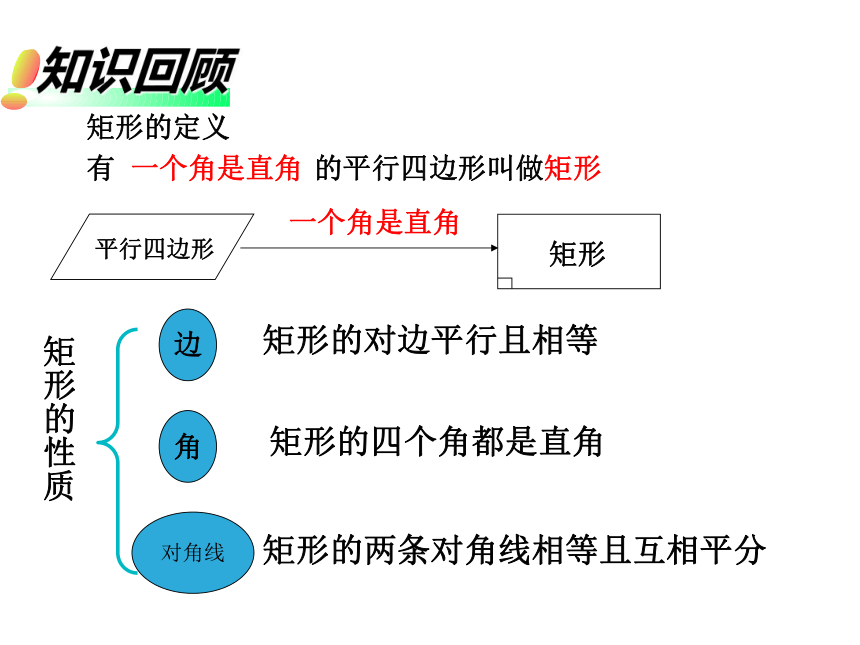
矩形的两条对角线相等且互相平分
矩形的对边平行且相等
矩形的四个角都是直角
边
对角线
角
矩形的定义
矩形的性质
一个角是直角
知识回顾
一天,小丽和吴娟到一个商店准备给今天要过生日的肖华买生日礼物,选了半天,她们俩最后决定买相框送给她,在里面摆放她们三个好朋友的相片,为了保证相框摆放的美观性,她们选择了矩形的相框,那么她们是用什么方法可以知道她们拿的就是矩形相框呢?
情境引入
思考:小丽和吴娟是怎样知道所买的相框是矩形的呢?
方法:通过测量四个角是直角
矩形的定义:
有一个角是直角的平行四边形是矩形.
思考:你还有其它的判定方法吗?
∠A=900
四边形ABCD是矩形
ABCD
新知学习
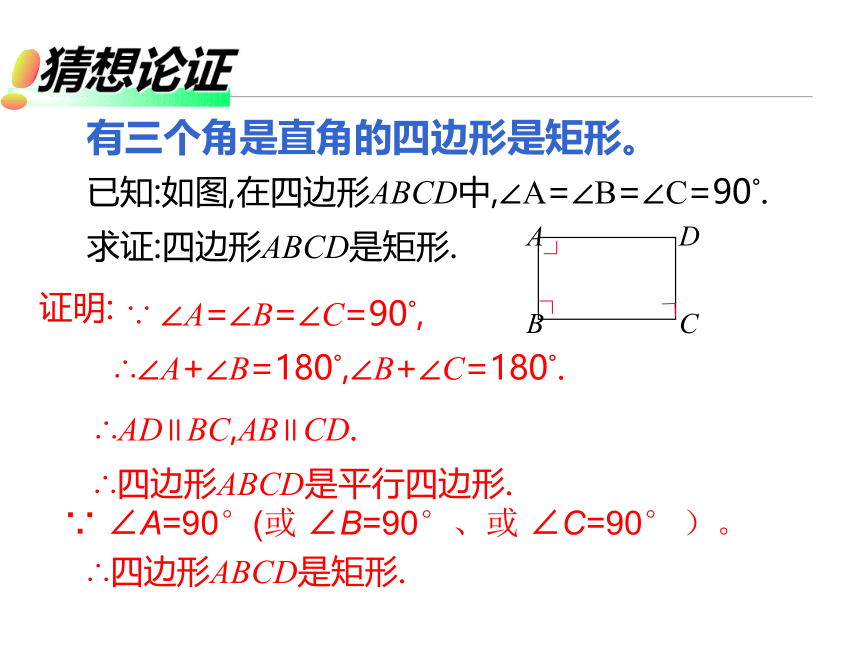
有三个角是直角的四边形是矩形。
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
证明:
∵
∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
D
B
C
A
∟
∟
∟
∵
∠A=90°(或
∠B=90°、或
∠C=90°
)。
猜想论证
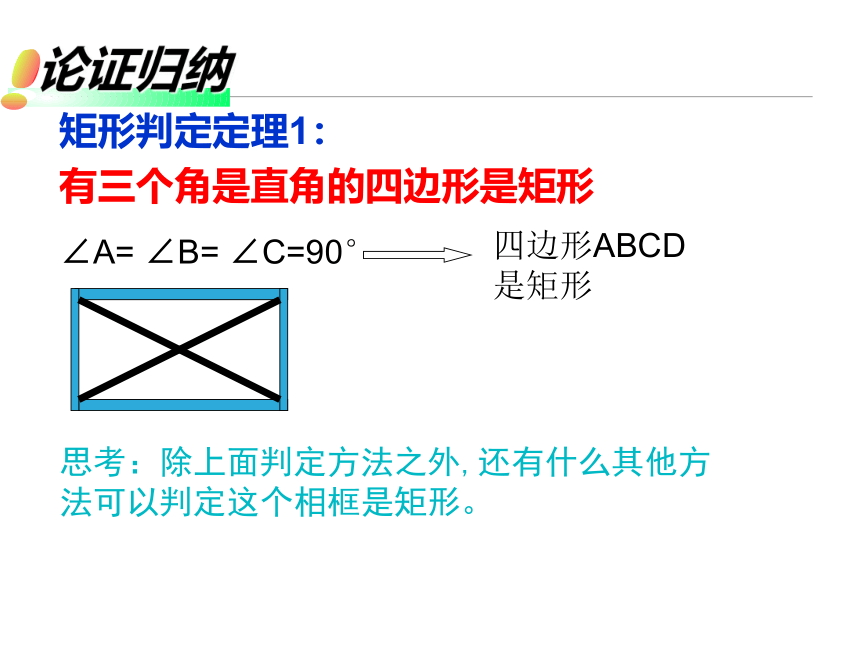
矩形判定定理1:
有三个角是直角的四边形是矩形
∠A=
∠B=
∠C=90°
四边形ABCD
是矩形
论证归纳
思考:除上面判定方法之外,还有什么其他方法可以判定这个相框是矩形。
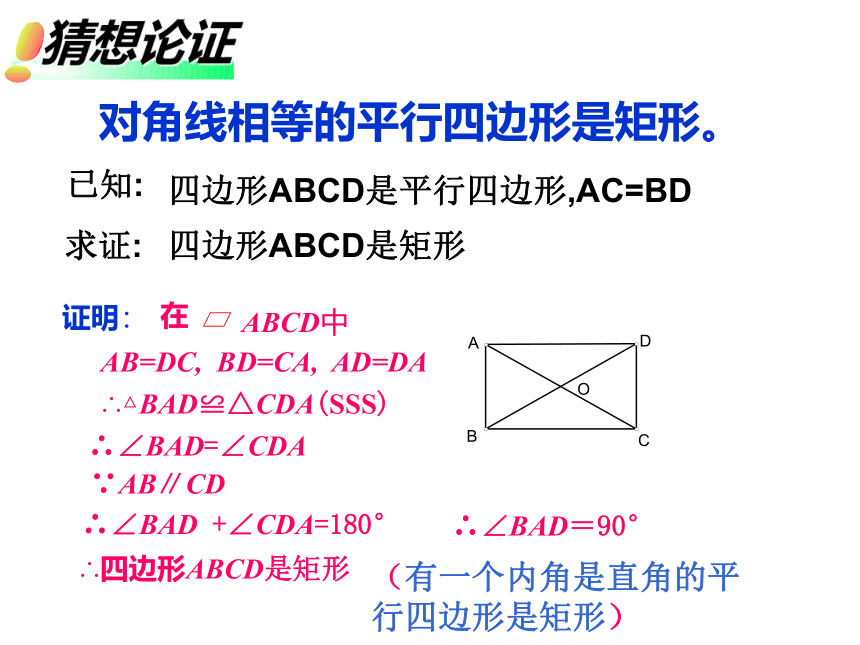
证明:
在
ABCD中
AB=DC,
BD=CA,
AD=DA
∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA
∵AB∥CD
∴∠BAD
+∠CDA=180°
∴∠BAD=90°
∴四边形ABCD是矩形
对角线相等的平行四边形是矩形。
四边形ABCD是平行四边形,AC=BD
四边形ABCD是矩形
已知:
求证:
(有一个内角是直角的平行四边形是矩形)
猜想论证
矩形判定定理2:
对角线相等的平行四边形是矩形。
几何语言:
∵四边形ABCD是平行四边形
AC=BD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形.)
A
B
C
D
O
(或OA=OC=OB=OD)
论证归纳
知识点
由直角的个数判定矩形
方法一(定义判定):有一个角是直角的平行四边形
是矩形;
方法二(角判定):有三个角是直角的四边形是矩形;
1
矩形的判定方法:
由对角线的关系判定矩形
知识点
2
方法三(对角线判定):对角线相等的平行四边形是矩
形;或对角线相等且互相平分的四边形是矩形.
(1)矩形具有而平行四边形不具有的性质(
)
(A)内角和是360度
(B)对角相等
(C)对边平行且相等
(D)对角线相等
(2)下面性质中,矩形不一定具有的是(
)
(A)对角线相等
(B)四个角相等
(C)是轴对称图形
(D)对角线垂直
D
D
一.选择题
课堂练习
二.判断题
对角线相等的四边形是矩形。(
)
对角线互相平分且相等的四边形是矩形。(
)
有一个角是直角的四边形是矩形。(
)
四个角都是直角的四边形是矩形。(
)
四个角都相等的四边形是矩形。(
)
对角线相等且互相垂直的四边形是矩形。(
)
课堂练习
例1:已知,如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO上的一点
,且AE=BF=CG=DH.求证四边形EFGH是矩形.
证明:
∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等)
AO=BO=CO=DO(矩形的对角线互相平分)
∵
AE=BF=CG=DH
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形(对角线
互相平分的四边形是平行四边形)
∵EO+OG=FO+OH
即EG=FH
∴四边形EFGH是矩形(对角线相等的平行四边形是矩形)
B
C
D
E
F
G
H
O
A
例题精讲
例2
如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M、N分别为BC、AD
的中点.
求证:四边形BMDN是矩形.
例题精讲
证明:
∵△ABD和△BCD是全等的正三角形,
∴∠ADB=∠CDB=60°.
又∵M、N分别为BC、AD的中点,
∴BN⊥AD,DM⊥BC,
∠BDM=30°,
∴∠DNB=∠DMB=90°,
∠MDN=∠ADB+∠BDM=90°,
∴四边形BMDN是矩形(有三个角是直角的四边形是矩形).
1.
如图,平行四边形ABCD中,∠1=∠2.
求证:四边形ABCD矩形
证明:∵四边形ABCD是平行四边形
∴AO=CO,BO=DO
(平行四边形对角线互相平分)
∵
∠1=∠2
∴AO=BO(等角对等边
)
∴AC=BD
∴四边形ABCD是矩形
(对角线相等的平行四边形是矩形)
综合运用
2.
如图,在平行四边形ABCD中,AB=6,
BC=8,
AC=10.求证四边形ABCD是矩形.
证明:∵
AB=6,BC=8,AC=10
且62+82=102
∴AB2+BC2=AC2
∴
∠B=900(勾股定理逆定理
)
∵
ABCD是平行四边形
∴四边形ABCD是矩形
(有一个角是直角的平行四边形是矩形)
综合运用
3.
如图,△ABC中,AB=AC,
AD、AE分别是∠A与∠A的外角的平分线,BE⊥AE.求证:
AB=DE。
证明:∵AB=AC,AD平分∠BAC
∴AD⊥BC,
∠1=
∠BAC
/2
(等腰三角形三线合一)
∵
AE平分∠BAF
∴
∠2=
∠BAF/2
∵
∠BAC
+
∠BAF=1800
∴
∠1+
∠2=(∠BAC
+
∠BAF)/2=900
∵
BE⊥AE
∴
∠BDA=
∠DAE=
∠BEA=900
∴四边形BDAE是矩形(有三个角
是直角的四边形是矩形)
1
2
F
综合运用
4.已知:如图,
???ABCD的四个内角的平分线分别相交于E、F、G、H,
求证:四边形
EFGH为矩形.
∴∠BGC=90°
同理可证∠AFB=∠AED=90°
∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形)
证明:∵AB∥CD
∴∠ABC+∠BCD=180°
∵BG平分∠ABC,CG平分∠BCD
???????????????????????????????????????
综合运用
1、判定矩形的方法有哪些?(学生小结):
(1)
一个角是直角的平行四边形
(2)
有三个角是直角的四边形
(3)
对角线相等的平行四边形
注:矩形的判定定理(1)、(3)的两个条件:
①是平行四边形,②有一个角是直角或对角线相等.
判定方定理(2)的两个条件是:
①是四边形,②有三个直角
——是矩形。
课堂小结
19.1.2
矩形的判定
一个角是直角
有
的平行四边形叫做矩形
矩形
平行四边形
矩形的两条对角线相等且互相平分
矩形的对边平行且相等
矩形的四个角都是直角
边
对角线
角
矩形的定义
矩形的性质
一个角是直角
知识回顾
一天,小丽和吴娟到一个商店准备给今天要过生日的肖华买生日礼物,选了半天,她们俩最后决定买相框送给她,在里面摆放她们三个好朋友的相片,为了保证相框摆放的美观性,她们选择了矩形的相框,那么她们是用什么方法可以知道她们拿的就是矩形相框呢?
情境引入
思考:小丽和吴娟是怎样知道所买的相框是矩形的呢?
方法:通过测量四个角是直角
矩形的定义:
有一个角是直角的平行四边形是矩形.
思考:你还有其它的判定方法吗?
∠A=900
四边形ABCD是矩形
ABCD
新知学习
有三个角是直角的四边形是矩形。
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
证明:
∵
∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
D
B
C
A
∟
∟
∟
∵
∠A=90°(或
∠B=90°、或
∠C=90°
)。
猜想论证
矩形判定定理1:
有三个角是直角的四边形是矩形
∠A=
∠B=
∠C=90°
四边形ABCD
是矩形
论证归纳
思考:除上面判定方法之外,还有什么其他方法可以判定这个相框是矩形。
证明:
在
ABCD中
AB=DC,
BD=CA,
AD=DA
∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA
∵AB∥CD
∴∠BAD
+∠CDA=180°
∴∠BAD=90°
∴四边形ABCD是矩形
对角线相等的平行四边形是矩形。
四边形ABCD是平行四边形,AC=BD
四边形ABCD是矩形
已知:
求证:
(有一个内角是直角的平行四边形是矩形)
猜想论证
矩形判定定理2:
对角线相等的平行四边形是矩形。
几何语言:
∵四边形ABCD是平行四边形
AC=BD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形.)
A
B
C
D
O
(或OA=OC=OB=OD)
论证归纳
知识点
由直角的个数判定矩形
方法一(定义判定):有一个角是直角的平行四边形
是矩形;
方法二(角判定):有三个角是直角的四边形是矩形;
1
矩形的判定方法:
由对角线的关系判定矩形
知识点
2
方法三(对角线判定):对角线相等的平行四边形是矩
形;或对角线相等且互相平分的四边形是矩形.
(1)矩形具有而平行四边形不具有的性质(
)
(A)内角和是360度
(B)对角相等
(C)对边平行且相等
(D)对角线相等
(2)下面性质中,矩形不一定具有的是(
)
(A)对角线相等
(B)四个角相等
(C)是轴对称图形
(D)对角线垂直
D
D
一.选择题
课堂练习
二.判断题
对角线相等的四边形是矩形。(
)
对角线互相平分且相等的四边形是矩形。(
)
有一个角是直角的四边形是矩形。(
)
四个角都是直角的四边形是矩形。(
)
四个角都相等的四边形是矩形。(
)
对角线相等且互相垂直的四边形是矩形。(
)
课堂练习
例1:已知,如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO上的一点
,且AE=BF=CG=DH.求证四边形EFGH是矩形.
证明:
∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等)
AO=BO=CO=DO(矩形的对角线互相平分)
∵
AE=BF=CG=DH
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形(对角线
互相平分的四边形是平行四边形)
∵EO+OG=FO+OH
即EG=FH
∴四边形EFGH是矩形(对角线相等的平行四边形是矩形)
B
C
D
E
F
G
H
O
A
例题精讲
例2
如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M、N分别为BC、AD
的中点.
求证:四边形BMDN是矩形.
例题精讲
证明:
∵△ABD和△BCD是全等的正三角形,
∴∠ADB=∠CDB=60°.
又∵M、N分别为BC、AD的中点,
∴BN⊥AD,DM⊥BC,
∠BDM=30°,
∴∠DNB=∠DMB=90°,
∠MDN=∠ADB+∠BDM=90°,
∴四边形BMDN是矩形(有三个角是直角的四边形是矩形).
1.
如图,平行四边形ABCD中,∠1=∠2.
求证:四边形ABCD矩形
证明:∵四边形ABCD是平行四边形
∴AO=CO,BO=DO
(平行四边形对角线互相平分)
∵
∠1=∠2
∴AO=BO(等角对等边
)
∴AC=BD
∴四边形ABCD是矩形
(对角线相等的平行四边形是矩形)
综合运用
2.
如图,在平行四边形ABCD中,AB=6,
BC=8,
AC=10.求证四边形ABCD是矩形.
证明:∵
AB=6,BC=8,AC=10
且62+82=102
∴AB2+BC2=AC2
∴
∠B=900(勾股定理逆定理
)
∵
ABCD是平行四边形
∴四边形ABCD是矩形
(有一个角是直角的平行四边形是矩形)
综合运用
3.
如图,△ABC中,AB=AC,
AD、AE分别是∠A与∠A的外角的平分线,BE⊥AE.求证:
AB=DE。
证明:∵AB=AC,AD平分∠BAC
∴AD⊥BC,
∠1=
∠BAC
/2
(等腰三角形三线合一)
∵
AE平分∠BAF
∴
∠2=
∠BAF/2
∵
∠BAC
+
∠BAF=1800
∴
∠1+
∠2=(∠BAC
+
∠BAF)/2=900
∵
BE⊥AE
∴
∠BDA=
∠DAE=
∠BEA=900
∴四边形BDAE是矩形(有三个角
是直角的四边形是矩形)
1
2
F
综合运用
4.已知:如图,
???ABCD的四个内角的平分线分别相交于E、F、G、H,
求证:四边形
EFGH为矩形.
∴∠BGC=90°
同理可证∠AFB=∠AED=90°
∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形)
证明:∵AB∥CD
∴∠ABC+∠BCD=180°
∵BG平分∠ABC,CG平分∠BCD
???????????????????????????????????????
综合运用
1、判定矩形的方法有哪些?(学生小结):
(1)
一个角是直角的平行四边形
(2)
有三个角是直角的四边形
(3)
对角线相等的平行四边形
注:矩形的判定定理(1)、(3)的两个条件:
①是平行四边形,②有一个角是直角或对角线相等.
判定方定理(2)的两个条件是:
①是四边形,②有三个直角
——是矩形。
课堂小结
