人教八下数学19.2.3一次函数与方程不等式 课件(18张ppt)
文档属性
| 名称 | 人教八下数学19.2.3一次函数与方程不等式 课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 746.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-12 08:29:30 | ||
图片预览



文档简介
(共18张PPT)
第十九章
一次函数
19.2
一次函数
学习目标:
1.认识一次函数与方程(组)、一元一次不等式之间的联系.会用函数观点解释方程和不等式及其解(解集)的意义;
2.经历用函数图象表示方程、不等式解的过程,进一步体会“以形表示数,以数解释形”的数形结合思想.
学习重点:
1、理解一次函数与方程(组)的联系.
2、能根据函数图象直接写出不等式的解集。
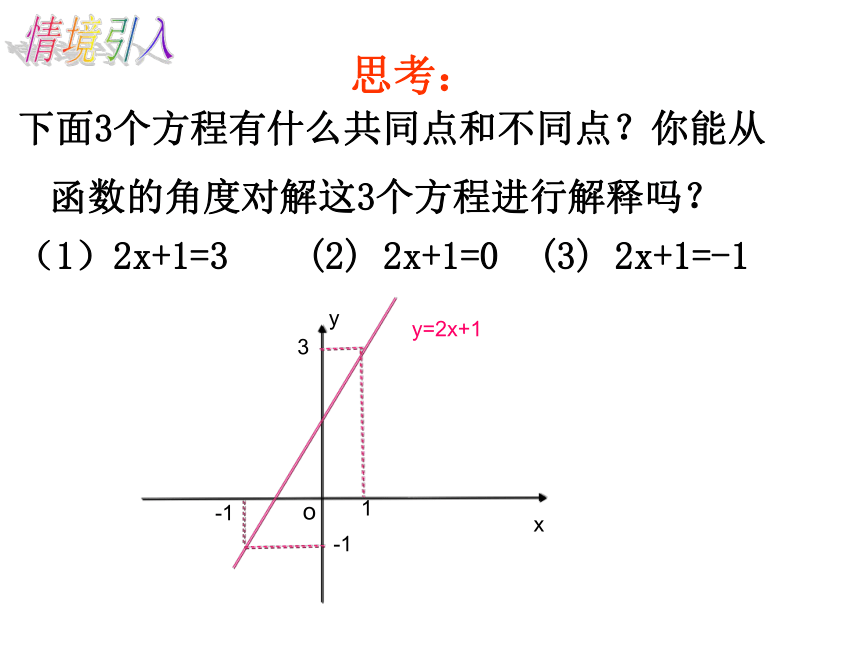
下面3个方程有什么共同点和不同点?你能从函数的角度对解这3个方程进行解释吗?
(1)2x+1=3
(2)
2x+1=0
(3)
2x+1=-1
思考:
3
1
x
y
o
这3个方程的等号左边都是2x+1,右边分别是3,0,-1。这3个方程相当于在一次函数y=2x+1的值分别为3,0,-1时,求自变量x的值。所以
解一元一次方程相当于在某个
一次函数y=ax+b的值为0时,
求自变量x的值。
x
y
3
-1
0
1
-1
(一)一次函数与方程
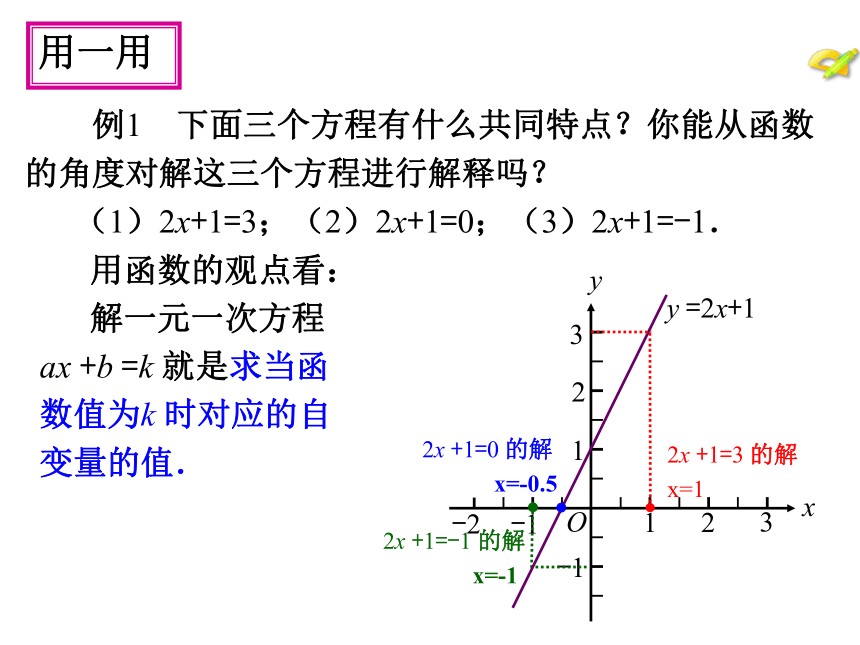
例1 下面三个方程有什么共同特点?你能从函数
的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
用函数的观点看:
解一元一次方程
ax
+b
=k
就是求当函
数值为k
时对应的自
变量的值.
用一用
2x
+1=3
的解
x=1
y
=2x+1
2x
+1=0
的解
x=-0.5
2x
+1=-1
的解
x=-1
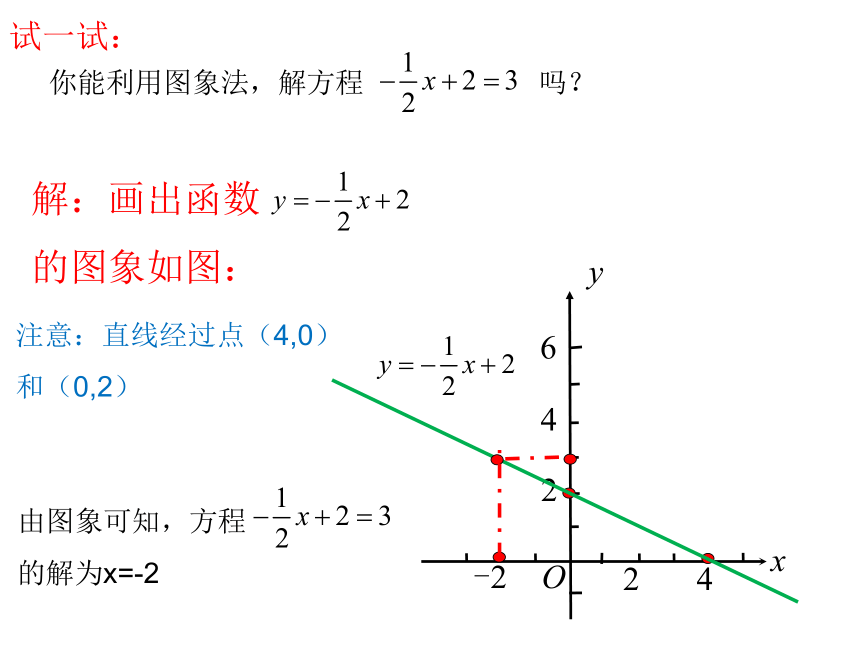
你能利用图象法,解方程
吗?
试一试:
解:画出函数
的图象如图:
注意:直线经过点(4,0)
和(0,2)
由图象可知,方程
的解为x=-2
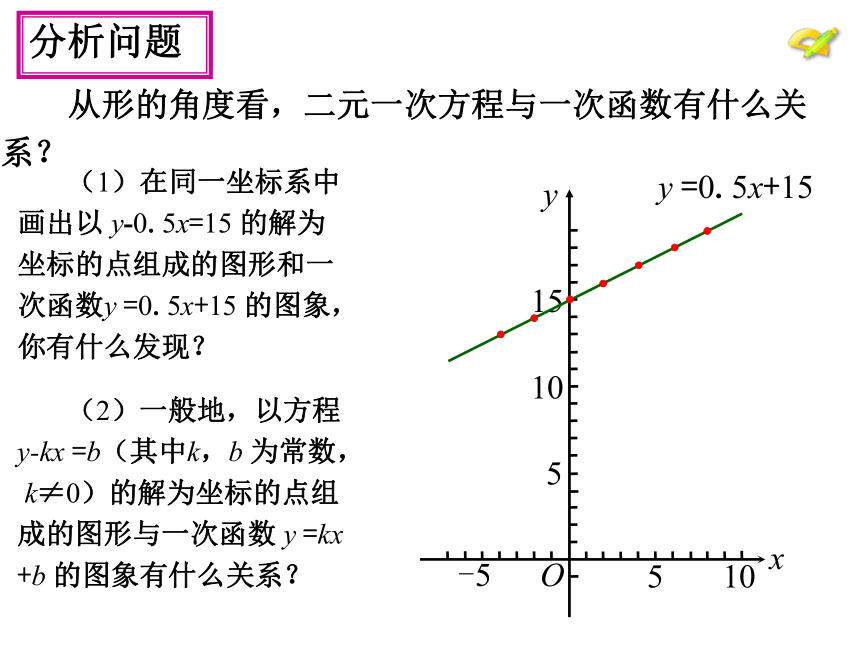
分析问题
(1)在同一坐标系中
画出以
y-0.5x=15
的解为
坐标的点组成的图形和一
次函数y
=0.5x+15
的图象,
你有什么发现?
从形的角度看,二元一次方程与一次函数有什么关
系?
(2)一般地,以方程
y-kx
=b(其中k,b
为常数,
k≠0)的解为坐标的点组
成的图形与一次函数
y
=kx
+b
的图象有什么关系?
二元一次方程与一次函数的关系
知识小结
一次函数
二元一次方程
1号探测气球从海拔5
m
处出发,以1
m/min
的速度上升.与此同时,2
号探测气球从海拔15
m
处出发,以0.5
m/min
的速度上升.两个气球都上升了1
h.
请用解析式分别表示两个气
球所在位置的海拔
y(m)与气球
上升时间
x(min)的函数关系.
拓展问题
气球1
海拔高度:y
=x+5;
气球2
海拔高度:y
=0.5x+15.
(二)一次函数与方程组
从数的角度看:
就是求自变量为何值时,两个
一次函数
y
=x+5,y
=0.5x+15
的函
数值相等,并求出函数值.
拓展问题
什么时刻,1
号气球的高度赶上2
号气球的高度?大
家会从数和形两方面分别加以研究吗?
气球1
海拔高度:y
=x+5
气球2
海拔高度:y
=0.5x+15
二元一次方程
组的解就是相应的
两个一次函数图象
的交点坐标.
拓展问题
A(20,25)
30
25
20
15
10
5
10
20
y
=x+5
y
=0.5x+15
15
5
O
x
y
从形的角度看,二元一次方程组与一次函数有什么
关系?
思考 下面三个不等式有什么共同特点?你能从函
数的角度对解这三个不等式进行解释吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
知识延伸
3个不等式
相同的特点是:不等号左边都是
;
不同点是:不等号及不等号右边分别是__,___,___.
2
0
-1
3x+2
(三)一次函数与不等式
思考
你能从函数的角度对解这三个不等式进行解释吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
y
=3x+2
y
=2
y
=-1
不等式3x+2>2的解集就是使函数y=3x+2的函数值大于2时所对于的自变量x的取值范围_______.
不等式3x+2<0的解集就是使函数y=3x+2的函数值小于0时所对于的自变量x的取值范围________.
不等式3x+2<-1的解集就是使函数y=3x+2的函数值小于-1时所对于的自变量x的取值范围______.
知识延伸
y
=0
x>0
x<-1
试一试
一次函数y=ax+b的图象如图所示:
由图象直接写出:
1.不等式ax+b>0的解集_______.
2.不等式ax+b<-4的解集_______.
3.不等式ax+b<-6的解集_______.
x>2
x<0
x<-1
当堂检测
1、如图,已知函数y=kx+b,观察图象回答下列问题:
(1)方程kx+b
=0的解;
(2)不等式kx+b
>0的解集;
(3)不等式kx+b
<0的解集;
(4)不等式-5<
kx+b
<0的解集;
x=3
x>3
x<3
0<x<3
2、某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通话时间x(分钟)与收费y(元)之间的函数关系如图所示.
当堂检测
根据函数图象回答:
1.有月租的是方式____,月租是_____元.
2.当通话时间x=______分钟时,两种收费相同,即方式①收费=方式②收费.
3.当通话时间
_____________分钟时,方式①收费<方式②收费.
3.当通话时间______________分钟时,方式①收费>方式②收费.
②
30
400
0≤X<400
X
>
400
作业:(课本99页,第8题,第12题)
8、当自变量x取何值时,函数y=5/2x+1与y=5x+17的值相等?这个函数值是多少?
12、(1)当b>0时,函数百y=x+b的图像经过哪几个象限??
(2)当b<0时,函数y=-x+b的图像经过哪几个象限?
(3)当k>0时,函数y=kx+1的图像经过哪几个象限?
(4)当k<0时,函数y=kx+1的图像经过哪几个象限?
作业答案:(课本99页,第8题,第12题)
8、当自变量x取何值时,函数y=
x+1与y=5x+17的值相等?这个函数值是多少?
解:由题意得:
x+1=5x+17
x=
.
∴y=-15.
当自变量
x=
时,函数值是-15.
12、
解(1)当b>0时,函数百y=x+b的图像经过一、二、三象限,?
(2)当b<0时,函数y=-x+b的图像经过二、三、四象限。
(3)当k>0时,函数y=kx+1的图像经过一、二、三象限,
(4)当k<0时,函数y=kx+1的图像经过一、二、四象限。
第十九章
一次函数
19.2
一次函数
学习目标:
1.认识一次函数与方程(组)、一元一次不等式之间的联系.会用函数观点解释方程和不等式及其解(解集)的意义;
2.经历用函数图象表示方程、不等式解的过程,进一步体会“以形表示数,以数解释形”的数形结合思想.
学习重点:
1、理解一次函数与方程(组)的联系.
2、能根据函数图象直接写出不等式的解集。
下面3个方程有什么共同点和不同点?你能从函数的角度对解这3个方程进行解释吗?
(1)2x+1=3
(2)
2x+1=0
(3)
2x+1=-1
思考:
3
1
x
y
o
这3个方程的等号左边都是2x+1,右边分别是3,0,-1。这3个方程相当于在一次函数y=2x+1的值分别为3,0,-1时,求自变量x的值。所以
解一元一次方程相当于在某个
一次函数y=ax+b的值为0时,
求自变量x的值。
x
y
3
-1
0
1
-1
(一)一次函数与方程
例1 下面三个方程有什么共同特点?你能从函数
的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
用函数的观点看:
解一元一次方程
ax
+b
=k
就是求当函
数值为k
时对应的自
变量的值.
用一用
2x
+1=3
的解
x=1
y
=2x+1
2x
+1=0
的解
x=-0.5
2x
+1=-1
的解
x=-1
你能利用图象法,解方程
吗?
试一试:
解:画出函数
的图象如图:
注意:直线经过点(4,0)
和(0,2)
由图象可知,方程
的解为x=-2
分析问题
(1)在同一坐标系中
画出以
y-0.5x=15
的解为
坐标的点组成的图形和一
次函数y
=0.5x+15
的图象,
你有什么发现?
从形的角度看,二元一次方程与一次函数有什么关
系?
(2)一般地,以方程
y-kx
=b(其中k,b
为常数,
k≠0)的解为坐标的点组
成的图形与一次函数
y
=kx
+b
的图象有什么关系?
二元一次方程与一次函数的关系
知识小结
一次函数
二元一次方程
1号探测气球从海拔5
m
处出发,以1
m/min
的速度上升.与此同时,2
号探测气球从海拔15
m
处出发,以0.5
m/min
的速度上升.两个气球都上升了1
h.
请用解析式分别表示两个气
球所在位置的海拔
y(m)与气球
上升时间
x(min)的函数关系.
拓展问题
气球1
海拔高度:y
=x+5;
气球2
海拔高度:y
=0.5x+15.
(二)一次函数与方程组
从数的角度看:
就是求自变量为何值时,两个
一次函数
y
=x+5,y
=0.5x+15
的函
数值相等,并求出函数值.
拓展问题
什么时刻,1
号气球的高度赶上2
号气球的高度?大
家会从数和形两方面分别加以研究吗?
气球1
海拔高度:y
=x+5
气球2
海拔高度:y
=0.5x+15
二元一次方程
组的解就是相应的
两个一次函数图象
的交点坐标.
拓展问题
A(20,25)
30
25
20
15
10
5
10
20
y
=x+5
y
=0.5x+15
15
5
O
x
y
从形的角度看,二元一次方程组与一次函数有什么
关系?
思考 下面三个不等式有什么共同特点?你能从函
数的角度对解这三个不等式进行解释吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
知识延伸
3个不等式
相同的特点是:不等号左边都是
;
不同点是:不等号及不等号右边分别是__,___,___.
2
0
-1
3x+2
(三)一次函数与不等式
思考
你能从函数的角度对解这三个不等式进行解释吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
y
=3x+2
y
=2
y
=-1
不等式3x+2>2的解集就是使函数y=3x+2的函数值大于2时所对于的自变量x的取值范围_______.
不等式3x+2<0的解集就是使函数y=3x+2的函数值小于0时所对于的自变量x的取值范围________.
不等式3x+2<-1的解集就是使函数y=3x+2的函数值小于-1时所对于的自变量x的取值范围______.
知识延伸
y
=0
x>0
x<-1
试一试
一次函数y=ax+b的图象如图所示:
由图象直接写出:
1.不等式ax+b>0的解集_______.
2.不等式ax+b<-4的解集_______.
3.不等式ax+b<-6的解集_______.
x>2
x<0
x<-1
当堂检测
1、如图,已知函数y=kx+b,观察图象回答下列问题:
(1)方程kx+b
=0的解;
(2)不等式kx+b
>0的解集;
(3)不等式kx+b
<0的解集;
(4)不等式-5<
kx+b
<0的解集;
x=3
x>3
x<3
0<x<3
2、某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通话时间x(分钟)与收费y(元)之间的函数关系如图所示.
当堂检测
根据函数图象回答:
1.有月租的是方式____,月租是_____元.
2.当通话时间x=______分钟时,两种收费相同,即方式①收费=方式②收费.
3.当通话时间
_____________分钟时,方式①收费<方式②收费.
3.当通话时间______________分钟时,方式①收费>方式②收费.
②
30
400
0≤X<400
X
>
400
作业:(课本99页,第8题,第12题)
8、当自变量x取何值时,函数y=5/2x+1与y=5x+17的值相等?这个函数值是多少?
12、(1)当b>0时,函数百y=x+b的图像经过哪几个象限??
(2)当b<0时,函数y=-x+b的图像经过哪几个象限?
(3)当k>0时,函数y=kx+1的图像经过哪几个象限?
(4)当k<0时,函数y=kx+1的图像经过哪几个象限?
作业答案:(课本99页,第8题,第12题)
8、当自变量x取何值时,函数y=
x+1与y=5x+17的值相等?这个函数值是多少?
解:由题意得:
x+1=5x+17
x=
.
∴y=-15.
当自变量
x=
时,函数值是-15.
12、
解(1)当b>0时,函数百y=x+b的图像经过一、二、三象限,?
(2)当b<0时,函数y=-x+b的图像经过二、三、四象限。
(3)当k>0时,函数y=kx+1的图像经过一、二、三象限,
(4)当k<0时,函数y=kx+1的图像经过一、二、四象限。
