算法初步
图片预览











文档简介
(共37张PPT)
1、把冰箱门打开 2、把大象装进去 3、把冰箱门关上
2000春晚小品《钟点工》
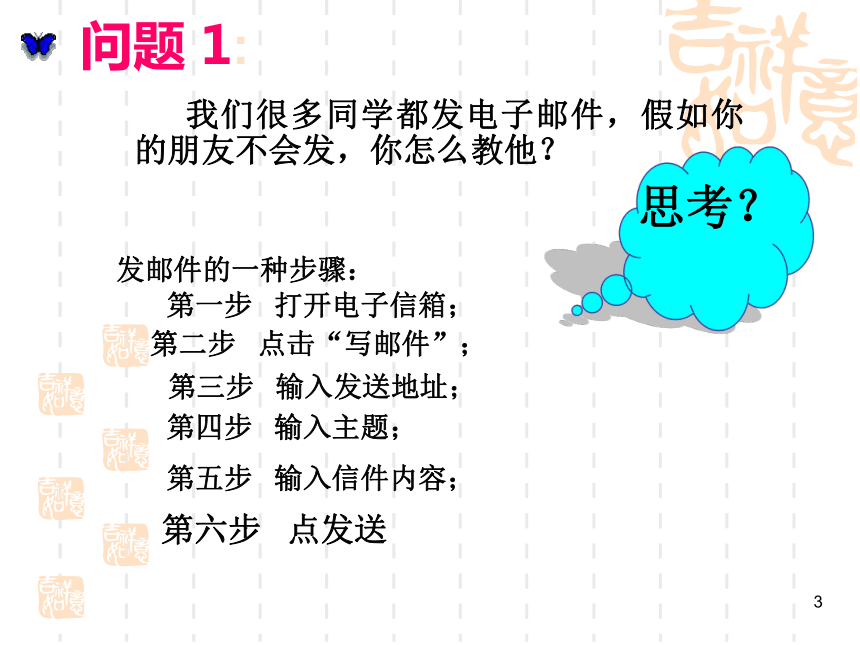
问题 1:
我们很多同学都发电子邮件,假如你的朋友不会发,你怎么教他?
第五步 输入信件内容;
思考?
第二步 点击“写邮件”;
发邮件的一种步骤:
第一步 打开电子信箱;
第三步 输入发送地址;
第四步 输入主题;
第六步 点发送
算法: 算法是解决一类问题的一系列步骤。
算法特点:
(1)有限性
(2)确定性
(3)不唯一性
我们日常生活中有哪些算法呢?
(4)有效 性
1.下面的四种叙述不能称为算法的是( )
(A)广播的广播操图解
(B)歌曲的歌谱
(C)做饭用米
(D)做米饭需要刷锅、淘米、添水、加热这些步骤
体验:
C
2.下列关于算法的说法正确的是( )
(A)某算法可以无止境地运算下去
(B)一个问题的算法步骤可以是可逆的
(C)完成一件事情的算法有且只有一种
(D)设计算法要本着简单、方便、可操作的原则
D
3.下列关于算法的说法中,正确的是( ).
A. 算法就是某个问题的解题过程
B. 算法执行后可以不产生确定的结果
C. 解决某类问题的算法不是惟一的
D. 算法可以无限地操作下去不停止
C
4.下列运算中不属于我们所讨论算法范畴的是( ).
A. 已知圆的半径求圆的面积
B. 从一副扑克牌随意抽取3张扑克牌抽到24点的可能性
C. 已知坐标平面内的两点求直线的方程
D. 加减乘除运算法则
B
5.下列语句表达中是算法的有( ).
① 从济南到巴黎可以先乘火车到北京再坐飞机抵达;
②利用公式 S = ah÷2 计算底为1高为2的三角形的面积; ③ x>2x +4;
④求M(1,2)与N(3,5)两点连线的方程可先求MN的斜率再利用点斜式方程求得.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
C
解:第一步:② - ①×2,得: 5y=3; ③
第三步:将
代入①,得
例1:解二元一次方程组:
第二步:解③得
体验 :写出解方程x2-2x-3=0的一个算法.
解:解法一:配方法
S1 移项,得x2-2x=3 ①
S2 ①式两边同加1并配方得 (x-1)2=4 ② S3 ②式两边开方,得x-1=±2 ③
S4 解③式得x=3或x=-1
解法二:因式分解法
S1 将方程左边因式分解得(x-3)(x+1)=0 ①
S2 由①得x-3=0或x+1=0 ②
S3 解②得x=3或x-1
解法三:公式法
S1 计算方程的判别式,判断其符号
△=(-2)2-4×(-3)>0;
S2 将a=1,b=-2,c=-3代入求根公式,
得x=3或x=-1
解决一个问题可能有多个算法,其中操作简单,步骤少且能解决一类问题的算法称为最优算法。
只要有公式可以利用,利用公式
决问题是最理想打得算法
练习:写出一元二次方程
的求解过程。
练习:解二元一次方程组:
课堂总结:
1.算法的概念;
2.算法的特点:
有限性;确定性;
有效;不唯一性。
3.解方程,方程组的算法。
一位商人有9枚银元,其中有1枚略轻的是假银元,你能用天平(不用砝码)将假银元找出来吗?
试 一 试
第一步:把九枚硬币平均分成三份,取其中两份放天平上称,若平衡则重的在剩下的一份里,若不平衡则在重的一份里;
第二步:在重的一份里取两枚放天平的两边,若平衡则剩下的一枚就是所找的,若不平衡则重的那枚就是所要找的。
例1:给定素数表,设计算法,将936分解成素因数的乘积。
判断936是否为素数
确定936的最小素因数
确定468的最小素因数
判断468是否为素数
判断234是否为素数
确定234的最小素因数
否
2
936=468 ×2
936=234 ×22
936=117 ×23
否
2
否
2
解:算法步骤如下:
判断117是否为素数
否
确定117的最小素因数
936=39 × 23 ×3
3
判断39是否为素数
否
确定39的最小素因数
3
936=13 × 23 ×32
判断13是否为素数
是
结束
∴ 936=13 × 23 ×32
9 3 6
4 6 8
2 3 4
1 1 7
3 9
2
2
2
3
1 3
3
例2:设计一个算法,求 840 与 1764 的最大公因数
解:算法步骤如下:1、先将840进行素因数分解:840= ;
2、然后将1764进行素因数分解1764= ;
3、确定它们的公共素因数:2,3,7;
4、确定公共素因数的指数:公共素因数2,3,7的指数分别为2,1,1;
5、最大公因数为:
1. 求18的所有正约数,设计两种算法;
小试身手
2. 求324,440的最大公因数及最小公倍数。
韩 信 点 兵
分析:(1)士兵的人数除以3余2;
(2)士兵的人数除以5余3;
(3)士兵的人数除以7余4;
猜数游戏
电视娱乐节目“幸运52”中,有一种有趣的“猜数”游戏:竞猜者如在规定的时间内猜出某种商品的价格,就可获得该件商品.
现在一商品,价格在0~1000元之间,采取怎样的策略,才能在较短的时间内说出正确的答案呢?
猜数游戏
案例1
在函数的应用部分,我们学习了用二分法求方程f(x)=0的近似解.如图所示
y
x
O
a
b
x*
二分法的基本思想是:将方程的有解区间分为两个小区间,然后判断解在哪个小区间;继续把有解的区间一分为二进行判断,如此周而复始,直到求出满足精度要求的近似解.
例1.求方程f(x)=x3+x2-1=0在区间 上的实数解,精确度为0.1.
解:1.因为f(0)=-1,f(1)=1,f(0)f(1)<0,则区 间 为有解区间,精度 1-0=1>0.1
2.取 的区间中点0.5;
3.计算f(0.5)= -0.125;
4.由于f(0.5)f(1)<0,可得新的有解区间
,精度1 – 0.5=0.5>0.1
6.计算f(0.75)= - 0.1563;
7.由于f(0.75)f(1)<0,可得新的有解区间 ,精度1-0.75=0.25>0.1
8.取区间 的中点0.875;
9.计算f(0.875)=0.43555
10.由于f(0.75)f(0.875)<0,可得
精度0.875-0.75=0.125>0.1;
11.取区间 的中点0.8125
5.取 的区间中点0.75;
11.计算f(0.8125)=0.19653
12.因f(0.75)f(0.8125)<0, 得区间 精度0.8125-0.75=0.0625<0.1
13.该区间一满足精确度的要求,所以取该区间的中点0.78125,它是方程的一个近似解.
1.确定有解区间 (f(a)f(b)<0).
2.取 的中点
3.计算函数f(x)在中点处的函数值
4.判断函数值 是否为零
如果为零, 就是方程的解,问题就得到解决.
f(a)
1)若 <0,则得新有解区间为
b) 如果函数值 不为零, 则分下列两种情形:
2)若 则确定新的有解
区间为
5.判断新的有解区间长度是否小于精确度:
(1)如果新的有解区间长度大于精确度,则在新的有解区间的基础上重复上述步骤;
(2)如果新的有解区间长度小于或等于精确度,则取新的有解区间的中点为方程的近似解.
简化写法:
第一步:令f(x)=x3+x2-1,因为f(0)f(1)<0,所以设x1=0,x2=1.
第二步:令m= ,判断f(m)是否为0,若是,则m为所求;若否,则继续判断f(x1)f(m)大于0还是小于0.
第三步:若f(x1)f(m)>0,则令x1= m;否则,令x2= m.
第四步:判断|x1-x2|<0.1是否成立 若是,则x1,x2之间的中间值为满足条件的近似根;若否,则返回第二步
算法,出现在12世纪,指的是运用阿拉伯数字进行算术运算的过程.在数学中,现代意义上的“算法”,通常指的是可以用计算机来解决来解决的某一类问题的程序或步骤,这些程序或步骤必须是明确的有效的,而且能够在有限步之内完成.
1、算法的含义:为一类问题的机械的、统一的求解方法
2、算法的特征 : 明确性、有效性、有限性
3、算法的思想 :程序化思思想
1、把冰箱门打开 2、把大象装进去 3、把冰箱门关上
2000春晚小品《钟点工》
问题 1:
我们很多同学都发电子邮件,假如你的朋友不会发,你怎么教他?
第五步 输入信件内容;
思考?
第二步 点击“写邮件”;
发邮件的一种步骤:
第一步 打开电子信箱;
第三步 输入发送地址;
第四步 输入主题;
第六步 点发送
算法: 算法是解决一类问题的一系列步骤。
算法特点:
(1)有限性
(2)确定性
(3)不唯一性
我们日常生活中有哪些算法呢?
(4)有效 性
1.下面的四种叙述不能称为算法的是( )
(A)广播的广播操图解
(B)歌曲的歌谱
(C)做饭用米
(D)做米饭需要刷锅、淘米、添水、加热这些步骤
体验:
C
2.下列关于算法的说法正确的是( )
(A)某算法可以无止境地运算下去
(B)一个问题的算法步骤可以是可逆的
(C)完成一件事情的算法有且只有一种
(D)设计算法要本着简单、方便、可操作的原则
D
3.下列关于算法的说法中,正确的是( ).
A. 算法就是某个问题的解题过程
B. 算法执行后可以不产生确定的结果
C. 解决某类问题的算法不是惟一的
D. 算法可以无限地操作下去不停止
C
4.下列运算中不属于我们所讨论算法范畴的是( ).
A. 已知圆的半径求圆的面积
B. 从一副扑克牌随意抽取3张扑克牌抽到24点的可能性
C. 已知坐标平面内的两点求直线的方程
D. 加减乘除运算法则
B
5.下列语句表达中是算法的有( ).
① 从济南到巴黎可以先乘火车到北京再坐飞机抵达;
②利用公式 S = ah÷2 计算底为1高为2的三角形的面积; ③ x>2x +4;
④求M(1,2)与N(3,5)两点连线的方程可先求MN的斜率再利用点斜式方程求得.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
C
解:第一步:② - ①×2,得: 5y=3; ③
第三步:将
代入①,得
例1:解二元一次方程组:
第二步:解③得
体验 :写出解方程x2-2x-3=0的一个算法.
解:解法一:配方法
S1 移项,得x2-2x=3 ①
S2 ①式两边同加1并配方得 (x-1)2=4 ② S3 ②式两边开方,得x-1=±2 ③
S4 解③式得x=3或x=-1
解法二:因式分解法
S1 将方程左边因式分解得(x-3)(x+1)=0 ①
S2 由①得x-3=0或x+1=0 ②
S3 解②得x=3或x-1
解法三:公式法
S1 计算方程的判别式,判断其符号
△=(-2)2-4×(-3)>0;
S2 将a=1,b=-2,c=-3代入求根公式,
得x=3或x=-1
解决一个问题可能有多个算法,其中操作简单,步骤少且能解决一类问题的算法称为最优算法。
只要有公式可以利用,利用公式
决问题是最理想打得算法
练习:写出一元二次方程
的求解过程。
练习:解二元一次方程组:
课堂总结:
1.算法的概念;
2.算法的特点:
有限性;确定性;
有效;不唯一性。
3.解方程,方程组的算法。
一位商人有9枚银元,其中有1枚略轻的是假银元,你能用天平(不用砝码)将假银元找出来吗?
试 一 试
第一步:把九枚硬币平均分成三份,取其中两份放天平上称,若平衡则重的在剩下的一份里,若不平衡则在重的一份里;
第二步:在重的一份里取两枚放天平的两边,若平衡则剩下的一枚就是所找的,若不平衡则重的那枚就是所要找的。
例1:给定素数表,设计算法,将936分解成素因数的乘积。
判断936是否为素数
确定936的最小素因数
确定468的最小素因数
判断468是否为素数
判断234是否为素数
确定234的最小素因数
否
2
936=468 ×2
936=234 ×22
936=117 ×23
否
2
否
2
解:算法步骤如下:
判断117是否为素数
否
确定117的最小素因数
936=39 × 23 ×3
3
判断39是否为素数
否
确定39的最小素因数
3
936=13 × 23 ×32
判断13是否为素数
是
结束
∴ 936=13 × 23 ×32
9 3 6
4 6 8
2 3 4
1 1 7
3 9
2
2
2
3
1 3
3
例2:设计一个算法,求 840 与 1764 的最大公因数
解:算法步骤如下:1、先将840进行素因数分解:840= ;
2、然后将1764进行素因数分解1764= ;
3、确定它们的公共素因数:2,3,7;
4、确定公共素因数的指数:公共素因数2,3,7的指数分别为2,1,1;
5、最大公因数为:
1. 求18的所有正约数,设计两种算法;
小试身手
2. 求324,440的最大公因数及最小公倍数。
韩 信 点 兵
分析:(1)士兵的人数除以3余2;
(2)士兵的人数除以5余3;
(3)士兵的人数除以7余4;
猜数游戏
电视娱乐节目“幸运52”中,有一种有趣的“猜数”游戏:竞猜者如在规定的时间内猜出某种商品的价格,就可获得该件商品.
现在一商品,价格在0~1000元之间,采取怎样的策略,才能在较短的时间内说出正确的答案呢?
猜数游戏
案例1
在函数的应用部分,我们学习了用二分法求方程f(x)=0的近似解.如图所示
y
x
O
a
b
x*
二分法的基本思想是:将方程的有解区间分为两个小区间,然后判断解在哪个小区间;继续把有解的区间一分为二进行判断,如此周而复始,直到求出满足精度要求的近似解.
例1.求方程f(x)=x3+x2-1=0在区间 上的实数解,精确度为0.1.
解:1.因为f(0)=-1,f(1)=1,f(0)f(1)<0,则区 间 为有解区间,精度 1-0=1>0.1
2.取 的区间中点0.5;
3.计算f(0.5)= -0.125;
4.由于f(0.5)f(1)<0,可得新的有解区间
,精度1 – 0.5=0.5>0.1
6.计算f(0.75)= - 0.1563;
7.由于f(0.75)f(1)<0,可得新的有解区间 ,精度1-0.75=0.25>0.1
8.取区间 的中点0.875;
9.计算f(0.875)=0.43555
10.由于f(0.75)f(0.875)<0,可得
精度0.875-0.75=0.125>0.1;
11.取区间 的中点0.8125
5.取 的区间中点0.75;
11.计算f(0.8125)=0.19653
12.因f(0.75)f(0.8125)<0, 得区间 精度0.8125-0.75=0.0625<0.1
13.该区间一满足精确度的要求,所以取该区间的中点0.78125,它是方程的一个近似解.
1.确定有解区间 (f(a)f(b)<0).
2.取 的中点
3.计算函数f(x)在中点处的函数值
4.判断函数值 是否为零
如果为零, 就是方程的解,问题就得到解决.
f(a)
1)若 <0,则得新有解区间为
b) 如果函数值 不为零, 则分下列两种情形:
2)若 则确定新的有解
区间为
5.判断新的有解区间长度是否小于精确度:
(1)如果新的有解区间长度大于精确度,则在新的有解区间的基础上重复上述步骤;
(2)如果新的有解区间长度小于或等于精确度,则取新的有解区间的中点为方程的近似解.
简化写法:
第一步:令f(x)=x3+x2-1,因为f(0)f(1)<0,所以设x1=0,x2=1.
第二步:令m= ,判断f(m)是否为0,若是,则m为所求;若否,则继续判断f(x1)f(m)大于0还是小于0.
第三步:若f(x1)f(m)>0,则令x1= m;否则,令x2= m.
第四步:判断|x1-x2|<0.1是否成立 若是,则x1,x2之间的中间值为满足条件的近似根;若否,则返回第二步
算法,出现在12世纪,指的是运用阿拉伯数字进行算术运算的过程.在数学中,现代意义上的“算法”,通常指的是可以用计算机来解决来解决的某一类问题的程序或步骤,这些程序或步骤必须是明确的有效的,而且能够在有限步之内完成.
1、算法的含义:为一类问题的机械的、统一的求解方法
2、算法的特征 : 明确性、有效性、有限性
3、算法的思想 :程序化思思想
