人教版数学八年级上册13.3.2等边三角形课件(共76张PPT)
文档属性
| 名称 | 人教版数学八年级上册13.3.2等边三角形课件(共76张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 686.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-13 00:17:32 | ||
图片预览






文档简介
(共76张PPT)
等边三角形
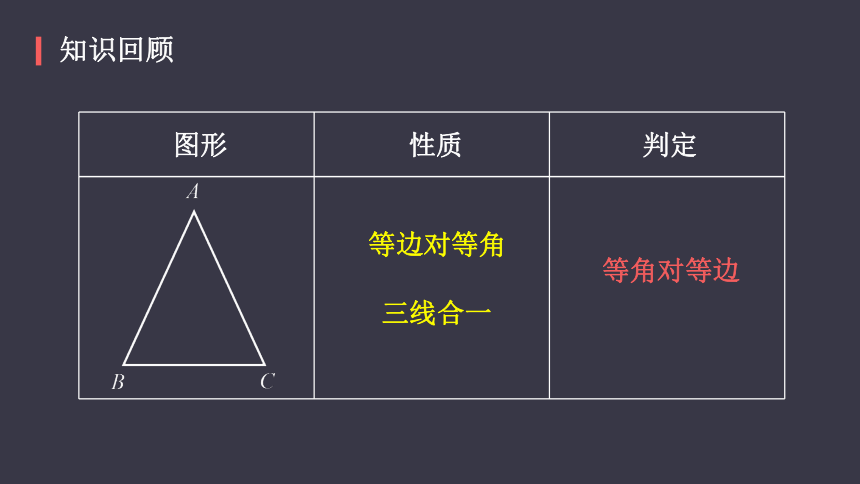
知识回顾
三线合一
等角对等边
图形
判定
性质
等边对等角
知识回顾
满足什么条件的三角形是等边三角形?
三边都相等的三角形是等边三角形
等边三角形也叫
正三角形
探究
等腰三角形有哪些特殊的性质呢??
从边的角度:
从角的角度:
从对称的角度:
两腰相等
等边对等角
三线合一
将等腰三角形的性质用于等边三角形,
你能得到什么结论??
猜想
结合等腰三角形的性质,
你能填出等边三角形对应的结论吗?
图形
轴对称图形
边
角
两边相等
两底角相等
底边上的
三线合一
三边相等
三角相等
都等于60°
三边的
三线合一
证明
等边三角形的三个内角都相等,
并且每一个角都等于60°
已知:△ABC
是等边三角形.求证:∠A
=∠B
=∠C=60°.
证明:∵ △ABC
是等边三角形,
∴ BC
=AC,BC
=AB.∴ ∠A
=∠B,∠A
=∠C
.∴ ∠A
=∠B
=∠C
.
∵ ∠A
+∠B
+∠C
=180°,
∴ ∠A
=60°.
∴ ∠A
=∠B
=∠C
=60°.
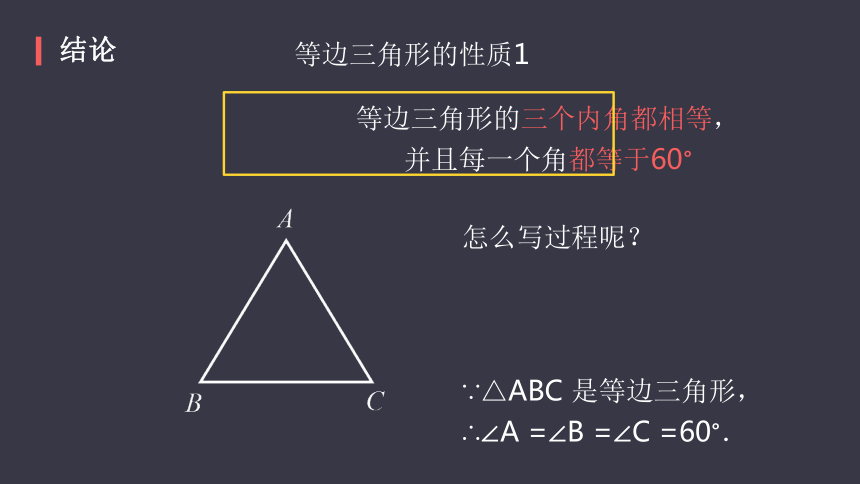
结论
等边三角形的性质1
等边三角形的三个内角都相等,
并且每一个角都等于60°
怎么写过程呢?
∵△ABC
是等边三角形,
∴∠A
=∠B
=∠C
=60°.
猜想
等边三角形是轴对称图形吗?
如果是,指出它的对称轴.
等边三角形是轴对称图形
等边三角形有三条对称轴
每条边上的中线、高和这条边所对的角的平分线所在的所有直线都是它的对称轴
等边三角形的每条边上的中线、高和这条边所对的角的平分线都分别重合.
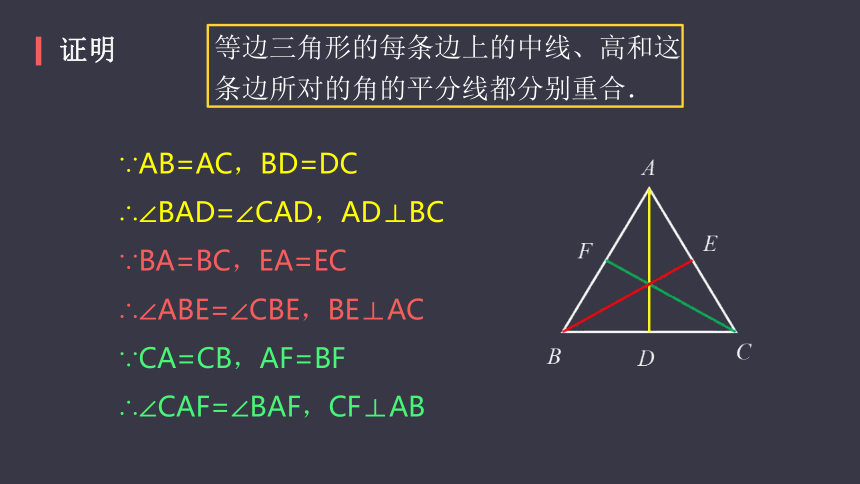
证明
等边三角形的每条边上的中线、高和这条边所对的角的平分线都分别重合.
∵AB=AC,BD=DC
∴∠BAD=∠CAD,AD⊥BC
∵BA=BC,EA=EC
∴∠ABE=∠CBE,BE⊥AC
∵CA=CB,AF=BF
∴∠CAF=∠BAF,CF⊥AB
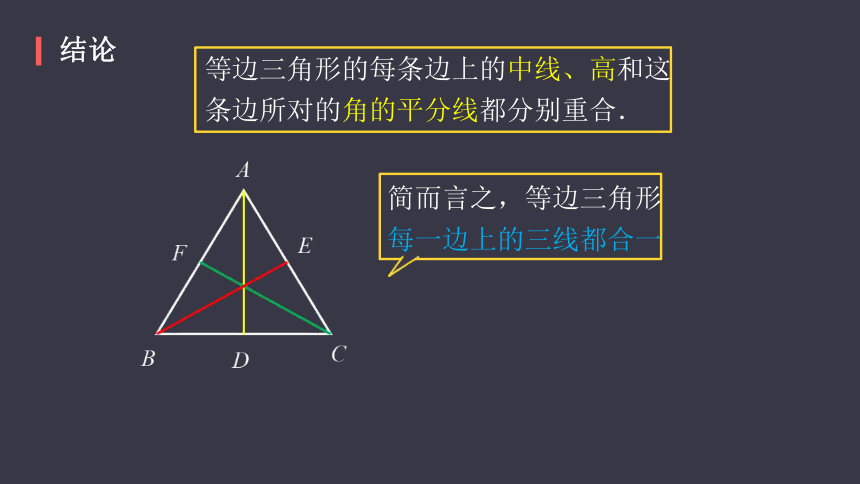
结论
等边三角形的每条边上的中线、高和这条边所对的角的平分线都分别重合.
简而言之,等边三角形
每一边上的三线都合一
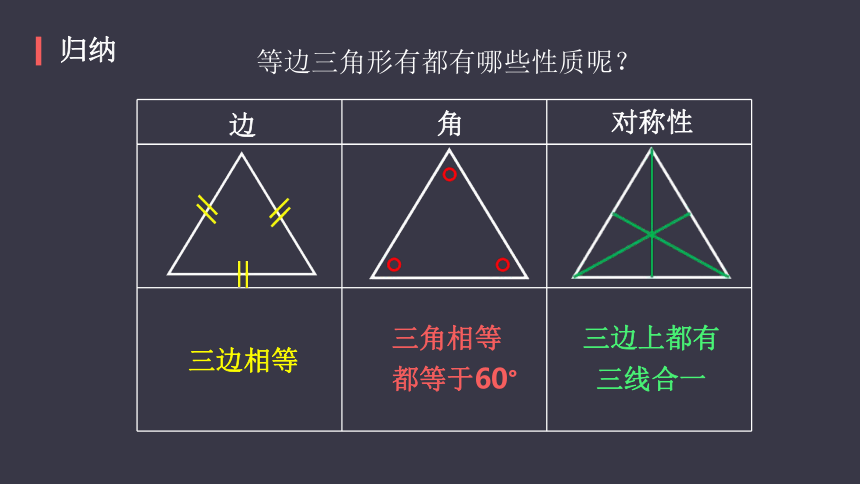
归纳
等边三角形有都有哪些性质呢?
三角相等
都等于60°
三边上都有三线合一
边
角
对称性
三边相等
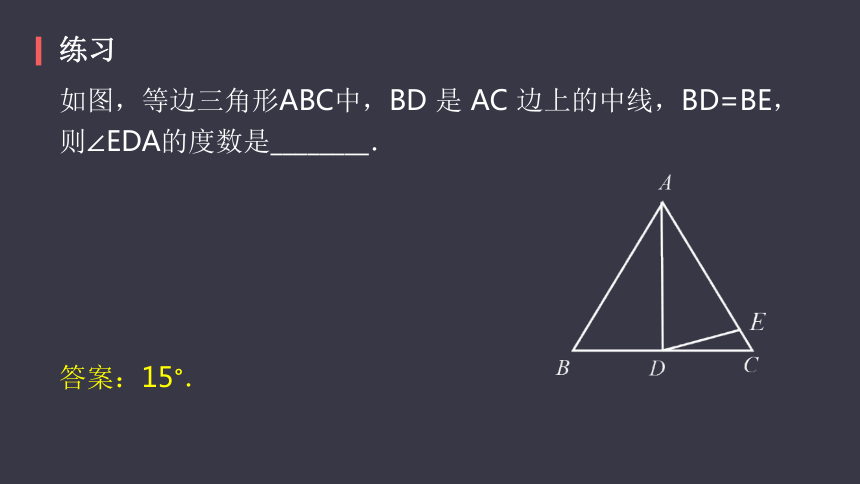
练习
如图,等边三角形ABC中,BD
是
AC
边上的中线,BD=BE,则∠EDA的度数是________.
答案:15°.
练习
如图,△ABC
是等边三角形,AD⊥AB于A,DC⊥BC
于C.求证:△DAC
是等腰三角形.
提示:证明∠DAC
=∠DCA.
练习
如图,已知,△ABC
是等边三角形,BD是中线,BD=6,延长BC到E.使CE=CD,求DE长.
提示:证明BD=DE.
思考
你知道怎么判定一个三角形是等边三角形吗?
可以利用定义,证明它的三边相等
除此之外,还有没有其他办法呢?
证明它三角相等行不行呢?
猜想:三个角都相等的三角形是等边三角形
证明
三个角都相等的三角形是等边三角形
已知:△ABC
中,∠A=∠B=∠C.
求证:△ABC
是等边三角形.
证明:∵∠A=∠B=∠C,
∴BC
=AC
=AB(等角对等边),
∴△ABC
是等边三角形.
思考
三边相等或三角相等都能直接判定一个三角形是等边三角形
除此之外还有没有其他判定方法呢?
我们知道,等边三角形是特殊的等腰三角形,
等腰三角形加个什么条件,能变成等边三角形呢?
有一个角是60°?
猜想
有一个角是60°的等腰三角形是等边三角形
这个60°角的位置有哪几种情况呢?
60°角是等腰三角形的顶角
60°角是等腰三角形的底角
证明
先证60°角是等腰三角形的顶角的情况
已知:△ABC,AB=AC,∠A=60°.
求证:△ABC
是等边三角形.
证明:∵∠A=60°,
∴∠B+∠C
=120°.
∵AB=AC,
∴∠B=∠C,
∴∠B=∠C
=60°,
∴∠A=∠B=∠C,
∴△ABC
是等边三角形.
证明
再证60°角是等腰三角形的底角的情况
已知:△ABC,AB=AC,∠B=60°.
求证:△ABC
是等边三角形.
证明:∵AB=AC,
∴∠B=∠C,
∵∠B=60°
∴∠B=∠C=60°,
∴∠A=60°,
∴∠A=∠B=∠C,
∴△ABC
是等边三角形.
归纳
要判定一个三角形是等边三角形有哪几种方法?
方法二
方法三
有一个角是60°的等腰三角形是等边三角形
三角相等的三角形是等边三角形
三边相等的三角形是等边三角形
方法一
例题
如图,△ABC
是等边三角形,DE∥BC,
分别交AB,AC
于点D,E.求证:△ADE
是等边三角形.
证明:
∵△ABC
是等边三角形,
∴∠A
=∠B
=∠C
=60°.
∵DE∥BC,
∴∠B
=∠ADE,∠C
=∠AED.
∴∠A=∠ADE
=∠AED.
∴△ADE
是等边三角形.
想一想,还有其他证法吗?
练习
如图,△ABC
是等边三角形,DE∥BC,
分别交AB,AC
的延长线于点D,E.求证:△ADE
是等边三角形.
证明:
∵△ABC
是等边三角形,
∴∠A
=∠B
=∠C
=60°.
∵DE∥BC,
∴∠B
=∠ADE,∠C
=∠AED.
∴∠A=∠ADE
=∠AED.
∴△ADE
是等边三角形.
练习
如图,△ABC
是等边三角形,DE∥BC,
分别交AB,AC
的方向延长线于点D,E.求证:△ADE
是等边三角形.
证明:
∵△ABC
是等边三角形,
∴∠A
=∠B
=∠C
=60°.
∵DE∥BC,
∴∠B
=∠ADE,∠C
=∠AED.
∴∠A=∠ADE
=∠AED.
∴△ADE
是等边三角形.
练习
已知:
D,E
分别是等边△ABC
中AB,AC
边上的点,且BD=CE.求证:△ABC
是等边三角形
.
提示:有一个角是60°的等腰三角形是等边三角形.
练习
已知△ABC
中,∠A
=60°,(
??????
?)
请你在括号内补充一个条件,使△ABC
能成为等边三角形.
答案:∠B=60°或∠C
=60°
或AB=BC
或AC
=BC.
练习
已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC
的周长为_______.
答案:9cm.
练习
△ABC
是等腰三角形,周长为15cm,且∠A=60°,则BC
=_______.
答案:5cm.
练习
如图,D、E、F分别是等边三角形ABC
三边上三点,且AD=BE=CF.试问:△DEF
是什么三角形?
提示:证明△ADF
≌△BED
≌△CFE.
练习
1.等边三角形是轴对称图形吗?如果是,指出它的对称轴.
练习
2.如图,等边三角形△ABC
中,AD是BC
边上的高,∠BDE=∠CDF=60°,图中与BD相等的线段有哪些?
探究
将两个含有30°的三角尺摆放在一起
你能借助这个图形,找到Rt△ABC?的直角BC?与斜边AB?之间的数量关系吗?
你能用学过的方法证明吗?
证明
如图,已知△ABC
≌△ADC,∠ACB=∠ACD=90°,∠BAC
=∠DAC
=30°.求证:
证明:∵△ABC≌△ADC,
∴AB=AD,
BC=CD,
又∵∠BAC=∠DAC=30°
∴∠BAD=
60°,
∴△ABD是等边三角形.
∴BD=AB,
∴BC=DC=
还有别的证法吗?
证明
如图,已知△ABC,∠ACB=90°,∠BAC
=30°.
求证:
证明:在BA上截取BD=BC,
∵∠BAC=30°,∠ACB=90°,
∴∠B=60°
∴△ABD是等边三角形,
∴BC=CD=BD,∠DCB=60°,
∴∠DCA=30°,
∴∠DCA=∠A,
∴AD=DC,
∴AD=BD=BC.
结论
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
这个定理该怎么写过程呢?
∵在Rt△ABC
中,
∠C
=90°,∠A=30°,
∴
例题
下图是屋架设计图的一部分,点D
是斜梁AB
的中点,立柱BC、
DE?垂直于横梁AC,AB=7.4m,∠A=30°,立柱BC
、
DE?要多长?
答案:3.7m,1.85m.
练习
在Rt△ABC
中,∠C
=90°
,∠B=2∠A
,∠B
和∠A各是多少度,边AB
和BC
之间有什么关系?
答案:60°,30°;AB=2BC.
练习
如图,在△ABC
中,∠C
=90°,∠A
=30°,AB
=10,则BC
的长为________.
答案:5.
练习
如图,在△ABC
中,∠ACB
=90°,CD
是高,∠A
=30°,AB
=4.则BD
=______
.?
答案:1.
练习
如图:在Rt△ABC中∠A=30°,AB+BC=12cm,则AB=_____cm.
答案:8.
练习
如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm,BD=_______,BE=_______.
答案:4cm,2cm.
练习
如图,在△ABC中,∠C
=90°,∠B=15°,DE
是AB
的中垂线,BE=5,则AE=______,AC
=_____.
答案:5,2.5.
练习
如图:已知
在△ABC
中,∠A=30°,
∠C
=90°,BD
平分∠ABC.求证:AD=2DC.
提示:证明∠DAC=30°.
等边共顶点
已知:如图,B,O,C
三点在一条直线上,△AOB
和△COD都是等边三角形,AC,BD
交于点
E
.
求证:(1)AC
=BD;(2)∠AEB=60°.
提示:证明△AOC
≌△BOD.
等边共顶点
如图,△ABC
和△DEC
都是等边三角形,连接BD、AE,且BD交AC
于F、AE
交CD
于H,连接FH.
(1)求证:BD=AE;
提示:证明△BCD
≌△ACE.
总结:等边共顶点就会有边角边全等.
等边共顶点
如图,△ABC
和△DEC
都是等边三角形,连接BD、AE,且BD交AC
于F、AE交CD
于H,连接FH.
(2)求证:CF=CH;
(3)判断△CFH是什么特殊三角形并说明理由.
提示:证明△BCF
≌△ACH.
等边内的点到三边的距离之和
如图,已知等边三角形ABC,P是三角形内一点,PD⊥BC,PE⊥AC,PF⊥AB,求证:PD+PE+PF是等于等边三角形的高.
提示:连接PA,PB,PC,利用面积相等.
含30°直角三角形的剖分
要把一块三角形的土地均匀分给甲
、
乙、丙三家农户去种植,如果∠C=90°,∠B=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.
构造含30°的直角三角形
如图,在△ABC
中,AB=AC,∠A=120°,AB
的垂直平分线MN交BC
于M,交AB
于N.求证:CM=2BM.
提示:连接AM.
构造含30°的直角三角形
如图,在△ABC
中,AB=AC,∠A=120°,EF
垂直平分AC
且交BC
于F.求证:BF=2CF.
提示:连接AF.
构造含30°的直角三角形
如图在△
ABC
中,
AB=AC
=2a,∠ABC
=∠ACB=15°,求△ABC
的面积.
提示:作出AB边上的高.
构造含30°的直角三角形
腰长为
2,底角为15°的等腰三角形的面积为_______.
提示:作出底边上的高.
答案:1.
等边与全等综合
如图,△ABC
为等边三角形,D,E
两点分别在
BC,AC
边上,AE=AD,AD,BE
相交点于
P,BQ⊥AD
于点
Q,若PQ=3,PE=1,求
AD
的长.
提示1:证明△ACD
≌△BAE.
提示2:∠BPQ=∠BAP+∠ABP.
等边与全等综合
已知:如图,在等边△ABC
中,D、E分别为BC、AC上的点,且AE=CD,连结AD、BE
交于点P,作BQ⊥AD
于Q,
求证:(1)∠APE=60°;(2)BP=2PQ.
提示1:证明△ABD
≌△BCE.
提示2:∠APE=∠BAP+∠ABP.
等边与全等综合
如图,在等边△ABC
中,AC=9,点
O
在
AB
上,且
BO=3,点
P
是
BC
上一动点,连结
OP,将线段
OP
绕点
O
逆时针旋转
60°
得到线段
OD.要使点
D
恰好落在
AC
上,则
BP
的长是_____.
提示:先画出示意图,然后证明△BOP
≌△ADO.
答案:6.
直角边是斜边的一半
已知:如图,在△ABC中,∠ACB=90°,BC=
?
?
?
AB.
求证:∠A=30°.
提示:延长BC
至D,使得CD=BC,连接AD.
总结:若直角边是斜边的一半,则直角边所对的角是30°.
与代数综合的问题
若三边长
a,b,c
满足(a-b)(b-c)(c-a)=0,则三角形的形状为____________.
答案:等腰三角形.
与代数综合的问题
若三边长
a,b,c
满足(a-b)
?+(b-c)
?+(c-a)
?=0,则三角形的形状为____________.
答案:等边三角形.
2
2
2
总结
这节课我们学到了什么?
等边三角形的性质
三角相等
都等于60°
三边上都有三线合一
三边相等
对称性
边
角
总结
这节课我们还学到了什么?
等边三角形的判定
方法一
方法二
方法三
三角相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形
三边相等的三角形是等边三角形
总结
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
这节课我们还学到了什么?
复习巩固
1.(1)等腰三角形的一个角是110°,它的另外两个角是多少度?
?
?(2)等腰三角形的一个角是80°,它的另外两个角是多少度?
复习巩固
2.如图,AD∥BC,BD平分∠ABC
.
求证AB=AD
.
复习巩固
3.如图,五角星的五个角都是顶角为36°的等腰三角形,为了画出五角星,还需要知道∠AMB
的度数
.
算一算∠AMB
等于多少度
.?
复习巩固
4.如图,厂房屋顶钢架外框是等腰三角形,其中AB=AC,立柱AD⊥BC,且顶角∠BAC=120°
.
∠B,∠C,∠BAD,∠CAD
各是多少度?
复习巩固
5.如图,∠A=∠B,CE∥DA,CE
交AB
于点E
.
求证:△CEB是等腰三角形
.
复习巩固
6.如图,点D,E在△ABC
的边BC上,AB=AC,AD=AE
.
求证BD=CE
.?
复习巩固
7.如图,AB=AC,∠A=40°,AB
的垂直平分线MN
交AC
于点D
.
求∠DBC
的度数
.?
综合运用
8.尺规作图:经过已知直线上的一点作这条直线的垂线
.?
综合运用
9.某地地震过后,河沿村中学的同学用下面的方法检测教室的房梁是否水平:
在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端挂一个铅锤,把这块三角尺的斜边贴在房梁上,结果线绳经过三角尺的直角顶点
.
同学们由此确信房梁是水平的
.
他们的判断对吗?为什么?
综合运用
10.如图,△ABC
中,BO
平分∠ABC,CO
平分∠ACB,MN
经过点O,与AB,AC
相交于点M,N,且MN∥BC
.
求证:△AMN
的周长等于AB+AC
.?
综合运用
11.上午8时,一条船从海岛A出发,以15
n
mile/h(海里/时,1
n
mile
=1
852
m)的速度向正北航行,10时到达海岛B
处
.
从A,B望灯塔C,测得∠NAC
=42°,∠NBC=84°.
求从海岛B
到灯塔C
的距离
.?
综合运用
12.如图,△ABD,△AEC都是等边三角形
.
求证BE=DC
.?
综合运用
11.等腰三角形两底角的平分线相等吗?两腰上的中线呢?两腰上的高呢?证明其中的一个结论
.?
拓广探索
14.如图,P,Q是△ABC
的边BC上的两点,并且BP=PQ=QC=AP=AQ,求∠BAC
的度数
.?
拓广探索
15.如图,要把一块三角形的土地均匀分给甲、乙、丙三家农户,如果∠C=90°,∠B=30°,要使这三家农户所得土地的大小、形状都相同,请你试着分一分,并在图上画出来
.?
等边三角形
知识回顾
三线合一
等角对等边
图形
判定
性质
等边对等角
知识回顾
满足什么条件的三角形是等边三角形?
三边都相等的三角形是等边三角形
等边三角形也叫
正三角形
探究
等腰三角形有哪些特殊的性质呢??
从边的角度:
从角的角度:
从对称的角度:
两腰相等
等边对等角
三线合一
将等腰三角形的性质用于等边三角形,
你能得到什么结论??
猜想
结合等腰三角形的性质,
你能填出等边三角形对应的结论吗?
图形
轴对称图形
边
角
两边相等
两底角相等
底边上的
三线合一
三边相等
三角相等
都等于60°
三边的
三线合一
证明
等边三角形的三个内角都相等,
并且每一个角都等于60°
已知:△ABC
是等边三角形.求证:∠A
=∠B
=∠C=60°.
证明:∵ △ABC
是等边三角形,
∴ BC
=AC,BC
=AB.∴ ∠A
=∠B,∠A
=∠C
.∴ ∠A
=∠B
=∠C
.
∵ ∠A
+∠B
+∠C
=180°,
∴ ∠A
=60°.
∴ ∠A
=∠B
=∠C
=60°.
结论
等边三角形的性质1
等边三角形的三个内角都相等,
并且每一个角都等于60°
怎么写过程呢?
∵△ABC
是等边三角形,
∴∠A
=∠B
=∠C
=60°.
猜想
等边三角形是轴对称图形吗?
如果是,指出它的对称轴.
等边三角形是轴对称图形
等边三角形有三条对称轴
每条边上的中线、高和这条边所对的角的平分线所在的所有直线都是它的对称轴
等边三角形的每条边上的中线、高和这条边所对的角的平分线都分别重合.
证明
等边三角形的每条边上的中线、高和这条边所对的角的平分线都分别重合.
∵AB=AC,BD=DC
∴∠BAD=∠CAD,AD⊥BC
∵BA=BC,EA=EC
∴∠ABE=∠CBE,BE⊥AC
∵CA=CB,AF=BF
∴∠CAF=∠BAF,CF⊥AB
结论
等边三角形的每条边上的中线、高和这条边所对的角的平分线都分别重合.
简而言之,等边三角形
每一边上的三线都合一
归纳
等边三角形有都有哪些性质呢?
三角相等
都等于60°
三边上都有三线合一
边
角
对称性
三边相等
练习
如图,等边三角形ABC中,BD
是
AC
边上的中线,BD=BE,则∠EDA的度数是________.
答案:15°.
练习
如图,△ABC
是等边三角形,AD⊥AB于A,DC⊥BC
于C.求证:△DAC
是等腰三角形.
提示:证明∠DAC
=∠DCA.
练习
如图,已知,△ABC
是等边三角形,BD是中线,BD=6,延长BC到E.使CE=CD,求DE长.
提示:证明BD=DE.
思考
你知道怎么判定一个三角形是等边三角形吗?
可以利用定义,证明它的三边相等
除此之外,还有没有其他办法呢?
证明它三角相等行不行呢?
猜想:三个角都相等的三角形是等边三角形
证明
三个角都相等的三角形是等边三角形
已知:△ABC
中,∠A=∠B=∠C.
求证:△ABC
是等边三角形.
证明:∵∠A=∠B=∠C,
∴BC
=AC
=AB(等角对等边),
∴△ABC
是等边三角形.
思考
三边相等或三角相等都能直接判定一个三角形是等边三角形
除此之外还有没有其他判定方法呢?
我们知道,等边三角形是特殊的等腰三角形,
等腰三角形加个什么条件,能变成等边三角形呢?
有一个角是60°?
猜想
有一个角是60°的等腰三角形是等边三角形
这个60°角的位置有哪几种情况呢?
60°角是等腰三角形的顶角
60°角是等腰三角形的底角
证明
先证60°角是等腰三角形的顶角的情况
已知:△ABC,AB=AC,∠A=60°.
求证:△ABC
是等边三角形.
证明:∵∠A=60°,
∴∠B+∠C
=120°.
∵AB=AC,
∴∠B=∠C,
∴∠B=∠C
=60°,
∴∠A=∠B=∠C,
∴△ABC
是等边三角形.
证明
再证60°角是等腰三角形的底角的情况
已知:△ABC,AB=AC,∠B=60°.
求证:△ABC
是等边三角形.
证明:∵AB=AC,
∴∠B=∠C,
∵∠B=60°
∴∠B=∠C=60°,
∴∠A=60°,
∴∠A=∠B=∠C,
∴△ABC
是等边三角形.
归纳
要判定一个三角形是等边三角形有哪几种方法?
方法二
方法三
有一个角是60°的等腰三角形是等边三角形
三角相等的三角形是等边三角形
三边相等的三角形是等边三角形
方法一
例题
如图,△ABC
是等边三角形,DE∥BC,
分别交AB,AC
于点D,E.求证:△ADE
是等边三角形.
证明:
∵△ABC
是等边三角形,
∴∠A
=∠B
=∠C
=60°.
∵DE∥BC,
∴∠B
=∠ADE,∠C
=∠AED.
∴∠A=∠ADE
=∠AED.
∴△ADE
是等边三角形.
想一想,还有其他证法吗?
练习
如图,△ABC
是等边三角形,DE∥BC,
分别交AB,AC
的延长线于点D,E.求证:△ADE
是等边三角形.
证明:
∵△ABC
是等边三角形,
∴∠A
=∠B
=∠C
=60°.
∵DE∥BC,
∴∠B
=∠ADE,∠C
=∠AED.
∴∠A=∠ADE
=∠AED.
∴△ADE
是等边三角形.
练习
如图,△ABC
是等边三角形,DE∥BC,
分别交AB,AC
的方向延长线于点D,E.求证:△ADE
是等边三角形.
证明:
∵△ABC
是等边三角形,
∴∠A
=∠B
=∠C
=60°.
∵DE∥BC,
∴∠B
=∠ADE,∠C
=∠AED.
∴∠A=∠ADE
=∠AED.
∴△ADE
是等边三角形.
练习
已知:
D,E
分别是等边△ABC
中AB,AC
边上的点,且BD=CE.求证:△ABC
是等边三角形
.
提示:有一个角是60°的等腰三角形是等边三角形.
练习
已知△ABC
中,∠A
=60°,(
??????
?)
请你在括号内补充一个条件,使△ABC
能成为等边三角形.
答案:∠B=60°或∠C
=60°
或AB=BC
或AC
=BC.
练习
已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC
的周长为_______.
答案:9cm.
练习
△ABC
是等腰三角形,周长为15cm,且∠A=60°,则BC
=_______.
答案:5cm.
练习
如图,D、E、F分别是等边三角形ABC
三边上三点,且AD=BE=CF.试问:△DEF
是什么三角形?
提示:证明△ADF
≌△BED
≌△CFE.
练习
1.等边三角形是轴对称图形吗?如果是,指出它的对称轴.
练习
2.如图,等边三角形△ABC
中,AD是BC
边上的高,∠BDE=∠CDF=60°,图中与BD相等的线段有哪些?
探究
将两个含有30°的三角尺摆放在一起
你能借助这个图形,找到Rt△ABC?的直角BC?与斜边AB?之间的数量关系吗?
你能用学过的方法证明吗?
证明
如图,已知△ABC
≌△ADC,∠ACB=∠ACD=90°,∠BAC
=∠DAC
=30°.求证:
证明:∵△ABC≌△ADC,
∴AB=AD,
BC=CD,
又∵∠BAC=∠DAC=30°
∴∠BAD=
60°,
∴△ABD是等边三角形.
∴BD=AB,
∴BC=DC=
还有别的证法吗?
证明
如图,已知△ABC,∠ACB=90°,∠BAC
=30°.
求证:
证明:在BA上截取BD=BC,
∵∠BAC=30°,∠ACB=90°,
∴∠B=60°
∴△ABD是等边三角形,
∴BC=CD=BD,∠DCB=60°,
∴∠DCA=30°,
∴∠DCA=∠A,
∴AD=DC,
∴AD=BD=BC.
结论
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
这个定理该怎么写过程呢?
∵在Rt△ABC
中,
∠C
=90°,∠A=30°,
∴
例题
下图是屋架设计图的一部分,点D
是斜梁AB
的中点,立柱BC、
DE?垂直于横梁AC,AB=7.4m,∠A=30°,立柱BC
、
DE?要多长?
答案:3.7m,1.85m.
练习
在Rt△ABC
中,∠C
=90°
,∠B=2∠A
,∠B
和∠A各是多少度,边AB
和BC
之间有什么关系?
答案:60°,30°;AB=2BC.
练习
如图,在△ABC
中,∠C
=90°,∠A
=30°,AB
=10,则BC
的长为________.
答案:5.
练习
如图,在△ABC
中,∠ACB
=90°,CD
是高,∠A
=30°,AB
=4.则BD
=______
.?
答案:1.
练习
如图:在Rt△ABC中∠A=30°,AB+BC=12cm,则AB=_____cm.
答案:8.
练习
如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm,BD=_______,BE=_______.
答案:4cm,2cm.
练习
如图,在△ABC中,∠C
=90°,∠B=15°,DE
是AB
的中垂线,BE=5,则AE=______,AC
=_____.
答案:5,2.5.
练习
如图:已知
在△ABC
中,∠A=30°,
∠C
=90°,BD
平分∠ABC.求证:AD=2DC.
提示:证明∠DAC=30°.
等边共顶点
已知:如图,B,O,C
三点在一条直线上,△AOB
和△COD都是等边三角形,AC,BD
交于点
E
.
求证:(1)AC
=BD;(2)∠AEB=60°.
提示:证明△AOC
≌△BOD.
等边共顶点
如图,△ABC
和△DEC
都是等边三角形,连接BD、AE,且BD交AC
于F、AE
交CD
于H,连接FH.
(1)求证:BD=AE;
提示:证明△BCD
≌△ACE.
总结:等边共顶点就会有边角边全等.
等边共顶点
如图,△ABC
和△DEC
都是等边三角形,连接BD、AE,且BD交AC
于F、AE交CD
于H,连接FH.
(2)求证:CF=CH;
(3)判断△CFH是什么特殊三角形并说明理由.
提示:证明△BCF
≌△ACH.
等边内的点到三边的距离之和
如图,已知等边三角形ABC,P是三角形内一点,PD⊥BC,PE⊥AC,PF⊥AB,求证:PD+PE+PF是等于等边三角形的高.
提示:连接PA,PB,PC,利用面积相等.
含30°直角三角形的剖分
要把一块三角形的土地均匀分给甲
、
乙、丙三家农户去种植,如果∠C=90°,∠B=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.
构造含30°的直角三角形
如图,在△ABC
中,AB=AC,∠A=120°,AB
的垂直平分线MN交BC
于M,交AB
于N.求证:CM=2BM.
提示:连接AM.
构造含30°的直角三角形
如图,在△ABC
中,AB=AC,∠A=120°,EF
垂直平分AC
且交BC
于F.求证:BF=2CF.
提示:连接AF.
构造含30°的直角三角形
如图在△
ABC
中,
AB=AC
=2a,∠ABC
=∠ACB=15°,求△ABC
的面积.
提示:作出AB边上的高.
构造含30°的直角三角形
腰长为
2,底角为15°的等腰三角形的面积为_______.
提示:作出底边上的高.
答案:1.
等边与全等综合
如图,△ABC
为等边三角形,D,E
两点分别在
BC,AC
边上,AE=AD,AD,BE
相交点于
P,BQ⊥AD
于点
Q,若PQ=3,PE=1,求
AD
的长.
提示1:证明△ACD
≌△BAE.
提示2:∠BPQ=∠BAP+∠ABP.
等边与全等综合
已知:如图,在等边△ABC
中,D、E分别为BC、AC上的点,且AE=CD,连结AD、BE
交于点P,作BQ⊥AD
于Q,
求证:(1)∠APE=60°;(2)BP=2PQ.
提示1:证明△ABD
≌△BCE.
提示2:∠APE=∠BAP+∠ABP.
等边与全等综合
如图,在等边△ABC
中,AC=9,点
O
在
AB
上,且
BO=3,点
P
是
BC
上一动点,连结
OP,将线段
OP
绕点
O
逆时针旋转
60°
得到线段
OD.要使点
D
恰好落在
AC
上,则
BP
的长是_____.
提示:先画出示意图,然后证明△BOP
≌△ADO.
答案:6.
直角边是斜边的一半
已知:如图,在△ABC中,∠ACB=90°,BC=
?
?
?
AB.
求证:∠A=30°.
提示:延长BC
至D,使得CD=BC,连接AD.
总结:若直角边是斜边的一半,则直角边所对的角是30°.
与代数综合的问题
若三边长
a,b,c
满足(a-b)(b-c)(c-a)=0,则三角形的形状为____________.
答案:等腰三角形.
与代数综合的问题
若三边长
a,b,c
满足(a-b)
?+(b-c)
?+(c-a)
?=0,则三角形的形状为____________.
答案:等边三角形.
2
2
2
总结
这节课我们学到了什么?
等边三角形的性质
三角相等
都等于60°
三边上都有三线合一
三边相等
对称性
边
角
总结
这节课我们还学到了什么?
等边三角形的判定
方法一
方法二
方法三
三角相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形
三边相等的三角形是等边三角形
总结
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
这节课我们还学到了什么?
复习巩固
1.(1)等腰三角形的一个角是110°,它的另外两个角是多少度?
?
?(2)等腰三角形的一个角是80°,它的另外两个角是多少度?
复习巩固
2.如图,AD∥BC,BD平分∠ABC
.
求证AB=AD
.
复习巩固
3.如图,五角星的五个角都是顶角为36°的等腰三角形,为了画出五角星,还需要知道∠AMB
的度数
.
算一算∠AMB
等于多少度
.?
复习巩固
4.如图,厂房屋顶钢架外框是等腰三角形,其中AB=AC,立柱AD⊥BC,且顶角∠BAC=120°
.
∠B,∠C,∠BAD,∠CAD
各是多少度?
复习巩固
5.如图,∠A=∠B,CE∥DA,CE
交AB
于点E
.
求证:△CEB是等腰三角形
.
复习巩固
6.如图,点D,E在△ABC
的边BC上,AB=AC,AD=AE
.
求证BD=CE
.?
复习巩固
7.如图,AB=AC,∠A=40°,AB
的垂直平分线MN
交AC
于点D
.
求∠DBC
的度数
.?
综合运用
8.尺规作图:经过已知直线上的一点作这条直线的垂线
.?
综合运用
9.某地地震过后,河沿村中学的同学用下面的方法检测教室的房梁是否水平:
在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端挂一个铅锤,把这块三角尺的斜边贴在房梁上,结果线绳经过三角尺的直角顶点
.
同学们由此确信房梁是水平的
.
他们的判断对吗?为什么?
综合运用
10.如图,△ABC
中,BO
平分∠ABC,CO
平分∠ACB,MN
经过点O,与AB,AC
相交于点M,N,且MN∥BC
.
求证:△AMN
的周长等于AB+AC
.?
综合运用
11.上午8时,一条船从海岛A出发,以15
n
mile/h(海里/时,1
n
mile
=1
852
m)的速度向正北航行,10时到达海岛B
处
.
从A,B望灯塔C,测得∠NAC
=42°,∠NBC=84°.
求从海岛B
到灯塔C
的距离
.?
综合运用
12.如图,△ABD,△AEC都是等边三角形
.
求证BE=DC
.?
综合运用
11.等腰三角形两底角的平分线相等吗?两腰上的中线呢?两腰上的高呢?证明其中的一个结论
.?
拓广探索
14.如图,P,Q是△ABC
的边BC上的两点,并且BP=PQ=QC=AP=AQ,求∠BAC
的度数
.?
拓广探索
15.如图,要把一块三角形的土地均匀分给甲、乙、丙三家农户,如果∠C=90°,∠B=30°,要使这三家农户所得土地的大小、形状都相同,请你试着分一分,并在图上画出来
.?
