人教版数学八年级上册13.3.1等腰三角形的判定课件(共52张ppt)
文档属性
| 名称 | 人教版数学八年级上册13.3.1等腰三角形的判定课件(共52张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 624.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-13 00:00:00 | ||
图片预览









文档简介
(共52张PPT)
等腰三角形的判定
知识回顾
等腰三角形的性质1:
等腰三角形的两个底角相等
简称为“等边对等角”
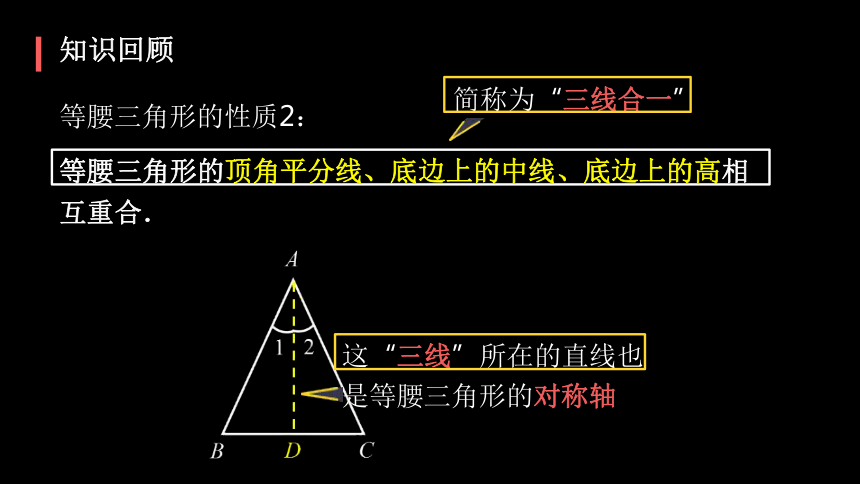
知识回顾
等腰三角形的性质2:
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
简称为“三线合一”
这“三线”所在的直线也是等腰三角形的对称轴
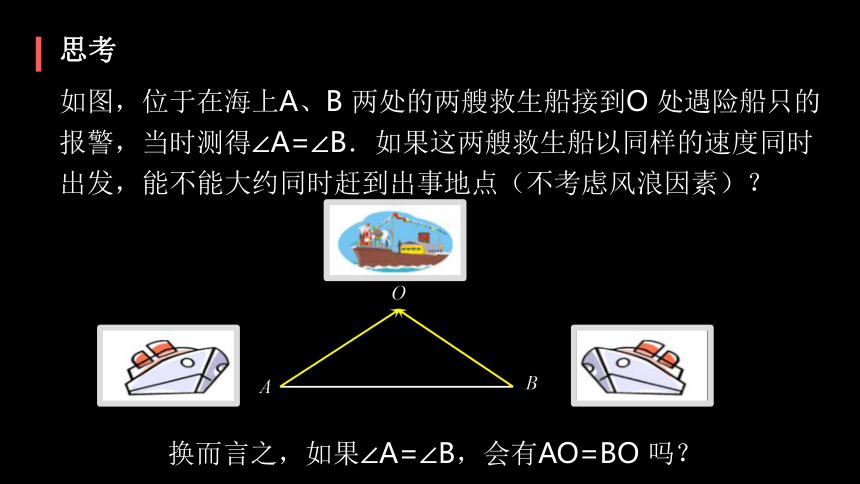
思考
如图,位于在海上A、B
两处的两艘救生船接到O
处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
换而言之,如果∠A=∠B,会有AO=BO
吗?
猜想与证明
如果一个三角形有两个角相等,
那么这两个角所对的边也相等.
你知道怎么证明吗?
先变成符号形式
已知:△ABC
中,∠B=∠C.
求证:AB=AC.
怎么证明边相等呢?
可以证三角形全等
没有全等怎么办呢?
可以构造
怎么构造呢?
可以作出顶角的平分线
猜想与证明
已知:△ABC
中,∠B=∠C.
求证:AB=AC.
证明:
作∠BAC
的平分线AD,
∴
∠
BAD=∠CAD.
在△BAD
和△CAD
中,
∠BAD=∠CAD,
∠B=∠C,
AD=AD
∴
△BAD
≌△CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
还有其他证法吗?
也可以过点A作高
猜想与证明
已知:△ABC
中,∠B=∠C.
求证:AB=AC.
证明:
作AD⊥BC
于点D,
∴
∠
ADB=∠ADC
=90°.
在△BAD
和△CAD中,
∠B=∠C,
∠ADB=∠ADC,
AD=AD
∴
△BAD
≌△CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
作角平分线和高都可以证明,作中线行吗?
猜想与证明
已知:△ABC
中,∠B=∠C.
求证:AB=AC.
证明:
取BC
中点D,连结AD,
∴
BD=CD.
在△BAD
和△CAD中,
AD=AD,
BD=CD,
∠B=∠C
这是边边角,
能判定全等吗?
不能
作中线不能证明这个结论
结论
等腰三角形的判定
如果一个三角形有两个角相等,
那么这两个角所对的边也相等.
简称为“等角对等边”
注意:“等角对等边”指的是都是同一个三角形中的边角关系.
等腰三角形的判定
在证明中怎么写过程呢?
在△ABC中,
∵
∠B=∠C
(
已知)
∴
AC=AB
(等边对等角)
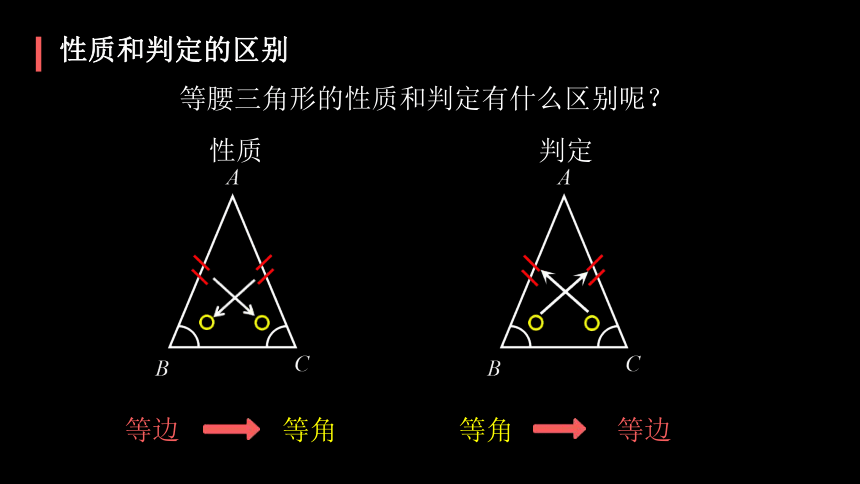
性质和判定的区别
等腰三角形的性质和判定有什么区别呢?
性质
判定
等边
等角
等角
等边
例题
求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:∠CAE是△ABC
的外角,AD平分∠CAE
AD∥BC.
求证:AB=AC.
∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠C(两直线平行,内错角相等)
∵AD平分∠CAE
,
∴∠1=∠2,
∴∠B=∠C,
∴
△ABC是等腰三角形.
证明:
练习
已知一个三角形的两个内角为50°和80°,则第三个角为_______,它是________三角形.
答案:50°,等腰.
练习
在△ABC
中,其两个内角如下,则能判定△ABC
为等腰三角形的是
(
)
C
A.∠A=40°,∠B=50°
B.∠A=40°,∠B=60°
C.∠A=40°,∠B=70°
D.∠A=40°,∠B=80°
练习
如图,∠A
=36°,AB=AC,BD平分∠
ABC,则图中一共有________个等腰三角形.
答案:3.
练习
如图,∠A
=36°,AB=AC,BD
平分∠
ABC,
CE平分∠
ACB
交BD
于点O,则图中一共有________个等腰三角形.
答案:8.
练习
如图,上午10
时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B
处,从A、B
望灯塔C,∠NAC=40°,∠NBC=80°.求从B
处到灯塔C
的距离.
提示:等角对等边.
提示:等角对等边.
练习
已知:如图,△ABC中,
∠
A=∠B=∠C.
求证:AB=AC=BC.
练习
如图△ABC
中,AB=AC,∠B=36°,D、E
分别是BC
边上两点,且∠ADE=∠AED=2∠BAD,则图中等腰三角形有____个.
答案:6.
练习
已知:如图,△ABC
的
BC
边上有
D,E
两点,∠1=∠2,∠3=∠4.求证:△ABC
是等腰三角形
.
提示:先证明∠B=∠C.
已知:如图,AD
∥BC,BD
平分∠ABC.
求证:AB=AD.
提示:先把相等的边标在图中.
总结:角平分线+平行→等腰.
角平分线+平行→等腰三角形
角平分线+平行→等腰三角形
如图,△ABC
中,∠ABC、∠ACB
的平分线交于点O,过点O作DE//BC,分别交AB、AC
于点D、E,求证:BD+EC=DE.
提示:角平分线+平行→等腰.
如图,BD是等腰三角形ABC的底边AC上的高,DE∥BC,交AB于点E.
判断△BDE是不是等腰三角形,并说明理由.
角平分线+平行→等腰三角形
提示:角平分线+平行→等腰.
角平分线+平行→等腰三角形
提示:角平分线+平行→等腰.
如图,△ABC
中,BI,CI
平分∠ABC,∠ACF,过点I
作ID∥BC
分别交AC,AB
于点E,D.若BD=9cm,CE=4cm,则DE
等于(?
?)
B
练习
1.如图,∠A
=36°,∠DBC
=36°,∠C
=72°,分别计算∠1,∠2的度数,并说明图中有哪些等腰三角形.
练习
2.如图,把一张矩形的纸沿对角线折叠,重合的部分是一个等腰三角形吗?为什么?
思考:“折叠”隐藏着什么条件呢?
所有的对应边相等,
所有的对应角相等.
看到折叠,就可以把等量关系标在图中.
提示:平行+角平分线→等腰.
练习
3.求证:如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形.
练习
4.如图,AC
和BD
相交于点O,且AB∥DC,OA
=OB.求证:OC
=OD.
例题
已知等腰三角形底边长为a
,底边上的高的长为h
,求作这个等腰三角形.
作法:
(1)作线段AB
=a;
(2)作线段AB
的垂直平分线MN,与AB
相交于点D;
(3)在MN上取一点C,使DC
=h;?
(4)连接AC,BC,则△ABC
就是所求作的等腰三角形.
如右图所示,△ABC
是等腰三角形,AB=AC,倘若一不留心.它的一部分被墨水涂没了,只留下一条底边BC
和一个底角∠C.同学们想一想,有没有办法把原来的等腰三角形ABC
重新画出来?大家试试看.
练习
方法一:用角的相等来画
方法二:用过一边中点作垂线的方法来画
角平分线+垂线
如图,已知△ABC
的面积为
12,AD平分∠BAC,且AD⊥BD
于点
D,则△ADC
的面积是
______.
提示:延长BD.
总结:角平分线+垂线→等腰三角形.
6
角平分线+垂线
提示:延长BE.
如图所示,在△ABC
中,AE
平分∠BAC,BE⊥AE,∠ABE
=2∠C.
求证:AC-AB=2BE.
角平分线+垂线
如图,已知等腰
Rt△ABC
中,AB
=
AC,∠BAC
=
90°,BF
平分∠ABC,CD
⊥
BD
交
BF的延长线于
D.求证:BF
=
2CD.
提示:延长CD.
与等角对等边有关的证明
已知:如图,
AD是△BAC
的平分线,E
为
BC
延长线上一点,∠EAC
=∠B,EF⊥AD????
于点
F
.
求证:EF
平分∠AEB.
提示:先证明△ADE是等腰三角形.
与等角对等边有关的证明
P是等腰三角形底边BC上的一点,过P
作PQ⊥BC
交AB
于Q,交CA的延长线于R.求证:△AQR是等腰三角形.
提示:先把等角在图中标出来.
与等角对等边有关的证明
P是等腰三角形底边BC所在直线上的一点,过P作PQ⊥BC交AB于Q,交CA的延长线于R,先补全图形,然后证明△AQR是等腰三角形.
提示:先把等角在图中标出来.
在△ABC
中,AD
平分∠BAC.BD
⊥
AD,垂足为
D,过
D
作DE∥AC,交
AB
于
E.
(1)求证:AE
=
DE;
(2)若
AB
=
8,求线段
DE
的长.
与等角对等边有关的证明
提示1:角平分线+平行→等腰三角形.
提示2:证明ED=EB.
与等角对等边有关的证明
已知:如图,四边形ABCD
中,AB=AD,∠B=∠D.
求证:BC=CD.
提示:连接BD.
等腰直角斜边中点模型
在△ABC
中,AB=AC,∠B=90°,点D、E
分别是AB、BC边上的动点,且BD与CE
相等,点M是AC
的中点,试探究在D、E
运动过程中,
△DEM
的形状是否发生变化,它是什么形状的三角形?
提示1:连接BM.
提示2:证明△BDM
≌△CEM.
等腰与全等综合
如图所示,在△ABC中,AB=AC,点
D,E,F
分别在
AB,BC,AC
边上,且BE=CF,BD=CE????.
(1)求证△DEF是等腰三角形
;
(2)当∠A=40°
时,求∠DEF的度数
.
提示:证△BED
≌△CFE.
答案:(2)70°.
等腰与全等综合
已知:如图,△ABC
中,AB=AC,D点在AB上,E点在AC
的延长线上,且BD=CE,连结DE,交BC
于F.
求证:DF=EF.
提示:过点D
做DP∥AC
.
总结:证线段相等,就要想到证全等,没有就得构造.
等腰与全等综合
已知:如图,△ABC
中,AB=AC,D点在AB上,E
点在AC
的延长线上,且DF=EF,连结DE,交BC
于F.
求证:BD=CE.
提示:过点D
做DP∥AC
.
总结:证线段相等,就要想到证全等,没有就得构造.
寻找满足等腰的点
如图,已知
Rt△ABC,∠C
=
90°,∠A
=
20°,在直线
BC
或
AC
上取一点
P,使得△PAB
是等腰三角形,则符合条件的
P
点有_______个.
答案:8.
寻找满足等腰的点
在正方形ABCD内找一点P,使△PAB、△PBC、△PCD、△PAD
都是等腰三角形,这样的P点有几个?在正方形ABCD
外呢?
利用二倍角构造等腰
当一个三角形中出现一个角是另一个角的2倍时,我们就可以通过转化倍角寻找到等腰三角形.
(1)如图中,若∠ABC=2∠C,如果作
BD
平分∠ABC,则△DBC
是等腰三角形.
利用二倍角构造等腰
当一个三角形中出现一个角是另一个角的
2倍时,我们就可以通过转化倍角寻找到等腰三角形.
(2)如图中,若∠ABC=2∠C,如果延长线
CB
到
D,使BD=BA,连结
AD,则△ADC
是等腰三角形.
利用二倍角构造等腰
当一个三角形中出现一个角是另一个角的
2倍时,我们就可以通过转化倍角寻找到等腰三角形.
(3)如图中,若∠ABC=2∠C,如果以
C
为角的顶点,CA
为角的一边,在形外作∠ACD=∠ACB,交
BA
的延长线于点D,则△DBC
是等腰三角形.
利用二倍角构造等腰
如图,∠ACB=2∠B,BC=2AC.求证:∠A=90°.
提示:作∠ACB
的平分线.
黄金三角形的剖分
如图,在△ABC中,AB=AC,
∠A=36°,你能把△ABC分成三个等腰三角形吗?(提供两中以上不同的作图方案)
黄金三角形的剖分
如图,在△ABC
中,AB=AC,
∠A=36°,你能把△ABC
分成三个等腰三角形吗?(提供两中以上不同的作图方案)
剖分出等腰三角形
在△ABC
中,∠ABC
=
30°,∠BAC
=
70°.在△ABC
所在平面内画一条直线,将△ABC
分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画几条?
提示:按剖分线所过的顶点分类.
总结
这节课我们学到了什么?
如果一个三角形有两个角相等,
那么这两个角所对的边也相等.
简称为“等角对等边”
注意:“等角对等边”指的是都是同一个三角形中的边角关系.
总结
等腰三角形的性质和判定有什么区别呢?
性质
判定
等边
等角
等角
等边
等腰三角形的判定
知识回顾
等腰三角形的性质1:
等腰三角形的两个底角相等
简称为“等边对等角”
知识回顾
等腰三角形的性质2:
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
简称为“三线合一”
这“三线”所在的直线也是等腰三角形的对称轴
思考
如图,位于在海上A、B
两处的两艘救生船接到O
处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
换而言之,如果∠A=∠B,会有AO=BO
吗?
猜想与证明
如果一个三角形有两个角相等,
那么这两个角所对的边也相等.
你知道怎么证明吗?
先变成符号形式
已知:△ABC
中,∠B=∠C.
求证:AB=AC.
怎么证明边相等呢?
可以证三角形全等
没有全等怎么办呢?
可以构造
怎么构造呢?
可以作出顶角的平分线
猜想与证明
已知:△ABC
中,∠B=∠C.
求证:AB=AC.
证明:
作∠BAC
的平分线AD,
∴
∠
BAD=∠CAD.
在△BAD
和△CAD
中,
∠BAD=∠CAD,
∠B=∠C,
AD=AD
∴
△BAD
≌△CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
还有其他证法吗?
也可以过点A作高
猜想与证明
已知:△ABC
中,∠B=∠C.
求证:AB=AC.
证明:
作AD⊥BC
于点D,
∴
∠
ADB=∠ADC
=90°.
在△BAD
和△CAD中,
∠B=∠C,
∠ADB=∠ADC,
AD=AD
∴
△BAD
≌△CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
作角平分线和高都可以证明,作中线行吗?
猜想与证明
已知:△ABC
中,∠B=∠C.
求证:AB=AC.
证明:
取BC
中点D,连结AD,
∴
BD=CD.
在△BAD
和△CAD中,
AD=AD,
BD=CD,
∠B=∠C
这是边边角,
能判定全等吗?
不能
作中线不能证明这个结论
结论
等腰三角形的判定
如果一个三角形有两个角相等,
那么这两个角所对的边也相等.
简称为“等角对等边”
注意:“等角对等边”指的是都是同一个三角形中的边角关系.
等腰三角形的判定
在证明中怎么写过程呢?
在△ABC中,
∵
∠B=∠C
(
已知)
∴
AC=AB
(等边对等角)
性质和判定的区别
等腰三角形的性质和判定有什么区别呢?
性质
判定
等边
等角
等角
等边
例题
求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:∠CAE是△ABC
的外角,AD平分∠CAE
AD∥BC.
求证:AB=AC.
∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠C(两直线平行,内错角相等)
∵AD平分∠CAE
,
∴∠1=∠2,
∴∠B=∠C,
∴
△ABC是等腰三角形.
证明:
练习
已知一个三角形的两个内角为50°和80°,则第三个角为_______,它是________三角形.
答案:50°,等腰.
练习
在△ABC
中,其两个内角如下,则能判定△ABC
为等腰三角形的是
(
)
C
A.∠A=40°,∠B=50°
B.∠A=40°,∠B=60°
C.∠A=40°,∠B=70°
D.∠A=40°,∠B=80°
练习
如图,∠A
=36°,AB=AC,BD平分∠
ABC,则图中一共有________个等腰三角形.
答案:3.
练习
如图,∠A
=36°,AB=AC,BD
平分∠
ABC,
CE平分∠
ACB
交BD
于点O,则图中一共有________个等腰三角形.
答案:8.
练习
如图,上午10
时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B
处,从A、B
望灯塔C,∠NAC=40°,∠NBC=80°.求从B
处到灯塔C
的距离.
提示:等角对等边.
提示:等角对等边.
练习
已知:如图,△ABC中,
∠
A=∠B=∠C.
求证:AB=AC=BC.
练习
如图△ABC
中,AB=AC,∠B=36°,D、E
分别是BC
边上两点,且∠ADE=∠AED=2∠BAD,则图中等腰三角形有____个.
答案:6.
练习
已知:如图,△ABC
的
BC
边上有
D,E
两点,∠1=∠2,∠3=∠4.求证:△ABC
是等腰三角形
.
提示:先证明∠B=∠C.
已知:如图,AD
∥BC,BD
平分∠ABC.
求证:AB=AD.
提示:先把相等的边标在图中.
总结:角平分线+平行→等腰.
角平分线+平行→等腰三角形
角平分线+平行→等腰三角形
如图,△ABC
中,∠ABC、∠ACB
的平分线交于点O,过点O作DE//BC,分别交AB、AC
于点D、E,求证:BD+EC=DE.
提示:角平分线+平行→等腰.
如图,BD是等腰三角形ABC的底边AC上的高,DE∥BC,交AB于点E.
判断△BDE是不是等腰三角形,并说明理由.
角平分线+平行→等腰三角形
提示:角平分线+平行→等腰.
角平分线+平行→等腰三角形
提示:角平分线+平行→等腰.
如图,△ABC
中,BI,CI
平分∠ABC,∠ACF,过点I
作ID∥BC
分别交AC,AB
于点E,D.若BD=9cm,CE=4cm,则DE
等于(?
?)
B
练习
1.如图,∠A
=36°,∠DBC
=36°,∠C
=72°,分别计算∠1,∠2的度数,并说明图中有哪些等腰三角形.
练习
2.如图,把一张矩形的纸沿对角线折叠,重合的部分是一个等腰三角形吗?为什么?
思考:“折叠”隐藏着什么条件呢?
所有的对应边相等,
所有的对应角相等.
看到折叠,就可以把等量关系标在图中.
提示:平行+角平分线→等腰.
练习
3.求证:如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形.
练习
4.如图,AC
和BD
相交于点O,且AB∥DC,OA
=OB.求证:OC
=OD.
例题
已知等腰三角形底边长为a
,底边上的高的长为h
,求作这个等腰三角形.
作法:
(1)作线段AB
=a;
(2)作线段AB
的垂直平分线MN,与AB
相交于点D;
(3)在MN上取一点C,使DC
=h;?
(4)连接AC,BC,则△ABC
就是所求作的等腰三角形.
如右图所示,△ABC
是等腰三角形,AB=AC,倘若一不留心.它的一部分被墨水涂没了,只留下一条底边BC
和一个底角∠C.同学们想一想,有没有办法把原来的等腰三角形ABC
重新画出来?大家试试看.
练习
方法一:用角的相等来画
方法二:用过一边中点作垂线的方法来画
角平分线+垂线
如图,已知△ABC
的面积为
12,AD平分∠BAC,且AD⊥BD
于点
D,则△ADC
的面积是
______.
提示:延长BD.
总结:角平分线+垂线→等腰三角形.
6
角平分线+垂线
提示:延长BE.
如图所示,在△ABC
中,AE
平分∠BAC,BE⊥AE,∠ABE
=2∠C.
求证:AC-AB=2BE.
角平分线+垂线
如图,已知等腰
Rt△ABC
中,AB
=
AC,∠BAC
=
90°,BF
平分∠ABC,CD
⊥
BD
交
BF的延长线于
D.求证:BF
=
2CD.
提示:延长CD.
与等角对等边有关的证明
已知:如图,
AD是△BAC
的平分线,E
为
BC
延长线上一点,∠EAC
=∠B,EF⊥AD????
于点
F
.
求证:EF
平分∠AEB.
提示:先证明△ADE是等腰三角形.
与等角对等边有关的证明
P是等腰三角形底边BC上的一点,过P
作PQ⊥BC
交AB
于Q,交CA的延长线于R.求证:△AQR是等腰三角形.
提示:先把等角在图中标出来.
与等角对等边有关的证明
P是等腰三角形底边BC所在直线上的一点,过P作PQ⊥BC交AB于Q,交CA的延长线于R,先补全图形,然后证明△AQR是等腰三角形.
提示:先把等角在图中标出来.
在△ABC
中,AD
平分∠BAC.BD
⊥
AD,垂足为
D,过
D
作DE∥AC,交
AB
于
E.
(1)求证:AE
=
DE;
(2)若
AB
=
8,求线段
DE
的长.
与等角对等边有关的证明
提示1:角平分线+平行→等腰三角形.
提示2:证明ED=EB.
与等角对等边有关的证明
已知:如图,四边形ABCD
中,AB=AD,∠B=∠D.
求证:BC=CD.
提示:连接BD.
等腰直角斜边中点模型
在△ABC
中,AB=AC,∠B=90°,点D、E
分别是AB、BC边上的动点,且BD与CE
相等,点M是AC
的中点,试探究在D、E
运动过程中,
△DEM
的形状是否发生变化,它是什么形状的三角形?
提示1:连接BM.
提示2:证明△BDM
≌△CEM.
等腰与全等综合
如图所示,在△ABC中,AB=AC,点
D,E,F
分别在
AB,BC,AC
边上,且BE=CF,BD=CE????.
(1)求证△DEF是等腰三角形
;
(2)当∠A=40°
时,求∠DEF的度数
.
提示:证△BED
≌△CFE.
答案:(2)70°.
等腰与全等综合
已知:如图,△ABC
中,AB=AC,D点在AB上,E点在AC
的延长线上,且BD=CE,连结DE,交BC
于F.
求证:DF=EF.
提示:过点D
做DP∥AC
.
总结:证线段相等,就要想到证全等,没有就得构造.
等腰与全等综合
已知:如图,△ABC
中,AB=AC,D点在AB上,E
点在AC
的延长线上,且DF=EF,连结DE,交BC
于F.
求证:BD=CE.
提示:过点D
做DP∥AC
.
总结:证线段相等,就要想到证全等,没有就得构造.
寻找满足等腰的点
如图,已知
Rt△ABC,∠C
=
90°,∠A
=
20°,在直线
BC
或
AC
上取一点
P,使得△PAB
是等腰三角形,则符合条件的
P
点有_______个.
答案:8.
寻找满足等腰的点
在正方形ABCD内找一点P,使△PAB、△PBC、△PCD、△PAD
都是等腰三角形,这样的P点有几个?在正方形ABCD
外呢?
利用二倍角构造等腰
当一个三角形中出现一个角是另一个角的2倍时,我们就可以通过转化倍角寻找到等腰三角形.
(1)如图中,若∠ABC=2∠C,如果作
BD
平分∠ABC,则△DBC
是等腰三角形.
利用二倍角构造等腰
当一个三角形中出现一个角是另一个角的
2倍时,我们就可以通过转化倍角寻找到等腰三角形.
(2)如图中,若∠ABC=2∠C,如果延长线
CB
到
D,使BD=BA,连结
AD,则△ADC
是等腰三角形.
利用二倍角构造等腰
当一个三角形中出现一个角是另一个角的
2倍时,我们就可以通过转化倍角寻找到等腰三角形.
(3)如图中,若∠ABC=2∠C,如果以
C
为角的顶点,CA
为角的一边,在形外作∠ACD=∠ACB,交
BA
的延长线于点D,则△DBC
是等腰三角形.
利用二倍角构造等腰
如图,∠ACB=2∠B,BC=2AC.求证:∠A=90°.
提示:作∠ACB
的平分线.
黄金三角形的剖分
如图,在△ABC中,AB=AC,
∠A=36°,你能把△ABC分成三个等腰三角形吗?(提供两中以上不同的作图方案)
黄金三角形的剖分
如图,在△ABC
中,AB=AC,
∠A=36°,你能把△ABC
分成三个等腰三角形吗?(提供两中以上不同的作图方案)
剖分出等腰三角形
在△ABC
中,∠ABC
=
30°,∠BAC
=
70°.在△ABC
所在平面内画一条直线,将△ABC
分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画几条?
提示:按剖分线所过的顶点分类.
总结
这节课我们学到了什么?
如果一个三角形有两个角相等,
那么这两个角所对的边也相等.
简称为“等角对等边”
注意:“等角对等边”指的是都是同一个三角形中的边角关系.
总结
等腰三角形的性质和判定有什么区别呢?
性质
判定
等边
等角
等角
等边
