苏科版八年级数学下册11.3《用反比例函数解决问题》课时练习含答案
文档属性
| 名称 | 苏科版八年级数学下册11.3《用反比例函数解决问题》课时练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 156.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-12 16:06:55 | ||
图片预览


文档简介
八年级数学11.3《用反比例函数解决问题》课时练习
一、选择题:
1、等腰三角形底角与顶角之间的函数关系是( )
A.正比例函数
B.一次函数
C.反比例函数
D.二次函数
2、已知水池的容量为50立方米,每时灌水量为n立方米,灌满水所需时间为t小时,那么t与n之间的函数关系式是
A.
t=50n
B.
t=50-n
C.
t=50/n
D.t=50+n
3、某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(h)变化的函数图象,其中BC段是双曲线y=k/x(k≠0)的一部分,则当x=16时,大棚内的温度约为???
A.18℃
B.15.5℃
C.
13.5℃
D.12℃
4、如图,市煤气公司计划在地下修建一个容积为104m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是
A.
B.
C.
D.
5、下列不是反比例函数图象的特点的是
(
)
A.图象是由两部分构成
B.图象与坐标轴无交点
C.图象要么总向右上方,要么总向右下方
D.图象在坐标轴相交而成的一对对顶角内
6、为了更好地保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的长方体污水处理池,池的底面积S(m2)与其深度h(m)满足关系式V=Sh(V≠0),则S关于h的函数图象大致是?
?
A.
B.
C.
D.
7、如果反比例函数y=k/x的图像经过点(-3,-4),那么函数的图像应在( )
A.第一、三象限
B.第一、二象限
C.第二、四象限
D.第三、四象限
8、春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过5min的集中药物喷洒,再封闭宿舍10min,然后打开门窗进行通风,室内每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(min)之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
A.经过5min集中喷洒药物,室内空气中的含药量最高达到10mg/m3
B.室内空气中的含药量不低于8mg/m3的持续时间达到了11min
C.当室内空气中的含药量不低于5mg/m3且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
D.当室内空气中的含药量低于2mg/m3时,对人体才是安全的,所以从室内空气中的含药量达到2mg/m3开始,需经过59min后,学生才能进入室内
二、填空题:
9、验光师测的一组关于近视眼镜的度数y与镜片的焦距x的数据,如表:则y关于x的函数关系式是________.
10、u与t成反比,且当u=6时,t=1/8,这个函数解析式为 .
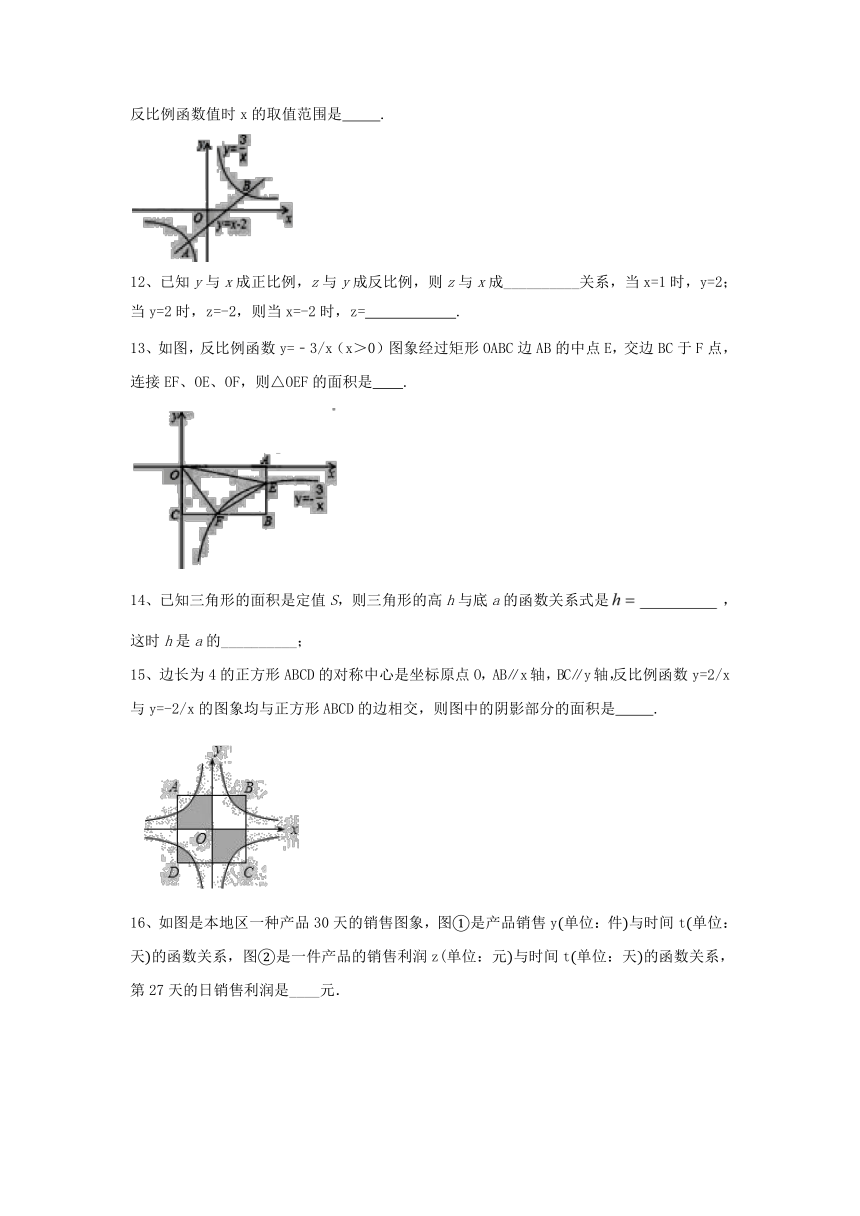
11、在图中,一次函数y=x﹣2与反比例函数y=3/x的图象交点为A、B.则一次函数值小于反比例函数值时x的取值范围是
.
12、已知y与x成正比例,z与y成反比例,则z与x成__________关系,当x=1时,y=2;当y=2时,z=-2,则当x=-2时,z=
.
13、如图,反比例函数y=﹣3/x(x>0)图象经过矩形OABC边AB的中点E,交边BC于F点,
连接EF、OE、OF,则△OEF的面积是
.
14、已知三角形的面积是定值S,则三角形的高h与底a的函数关系式是,这时h是a的__________;
15、边长为4的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴,反比例函数y=2/x与y=-2/x的图象均与正方形ABCD的边相交,则图中的阴影部分的面积是
.
16、如图是本地区一种产品30天的销售图象,图是产品销售y单位:件与时间t单位:天的函数关系,图是一件产品的销售利润z(单位:元与时间t单位:天的函数关系,第27天的日销售利润是____元.
三、解答题:
17、如图,A、B两点在反比例函数y=4/x上,分别经过A、B两点向轴作垂线段,已知图中阴影部分面积S阴影=1,求图中S1+S2部分的面积?
18、在某一电路中,保持电压U(伏特)不变,电流I(安培)与电阻R(欧姆)成反比例,当电阻R=5伏特时,电流I=2安培。
(1)求I与R之间的函数关系式。
(2)当电流I=0.5安培时,求电阻R的值。
19、已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).
(1)求v关于t的函数表达式.
(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
20、我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=k/x的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
3一天24小时大棚内温度超过12℃的时间有多少小时?
21、心理学家研究发现,一般情况下,一节课
40
分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数
y随时间x(分钟)的变化规律如右图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲
19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
参考答案
一、选择题:
1、B
2、
C
3、C
4、
A
5、
C
6、C
7、A
8、C
二、填空题:
9、y=100/x
10、u=48t
11、x<﹣1
或
0<x<3
12、反比例
1
13、2.25
14、h=2S/a
反比例函数
15、8
16、875
三、解答题:
17、6
18、(1)I=U/R
(2)20欧姆
19、(1)
v=100/t;
(2)
平均每小时至少要卸货20吨.
20、(1)10小时
(2)216
(3)17.2小时
21、(1)
第
30
分钟注意力更集中.
(2)
经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
一、选择题:
1、等腰三角形底角与顶角之间的函数关系是( )
A.正比例函数
B.一次函数
C.反比例函数
D.二次函数
2、已知水池的容量为50立方米,每时灌水量为n立方米,灌满水所需时间为t小时,那么t与n之间的函数关系式是
A.
t=50n
B.
t=50-n
C.
t=50/n
D.t=50+n
3、某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(h)变化的函数图象,其中BC段是双曲线y=k/x(k≠0)的一部分,则当x=16时,大棚内的温度约为???
A.18℃
B.15.5℃
C.
13.5℃
D.12℃
4、如图,市煤气公司计划在地下修建一个容积为104m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是
A.
B.
C.
D.
5、下列不是反比例函数图象的特点的是
(
)
A.图象是由两部分构成
B.图象与坐标轴无交点
C.图象要么总向右上方,要么总向右下方
D.图象在坐标轴相交而成的一对对顶角内
6、为了更好地保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的长方体污水处理池,池的底面积S(m2)与其深度h(m)满足关系式V=Sh(V≠0),则S关于h的函数图象大致是?
?
A.
B.
C.
D.
7、如果反比例函数y=k/x的图像经过点(-3,-4),那么函数的图像应在( )
A.第一、三象限
B.第一、二象限
C.第二、四象限
D.第三、四象限
8、春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过5min的集中药物喷洒,再封闭宿舍10min,然后打开门窗进行通风,室内每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(min)之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
A.经过5min集中喷洒药物,室内空气中的含药量最高达到10mg/m3
B.室内空气中的含药量不低于8mg/m3的持续时间达到了11min
C.当室内空气中的含药量不低于5mg/m3且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
D.当室内空气中的含药量低于2mg/m3时,对人体才是安全的,所以从室内空气中的含药量达到2mg/m3开始,需经过59min后,学生才能进入室内
二、填空题:
9、验光师测的一组关于近视眼镜的度数y与镜片的焦距x的数据,如表:则y关于x的函数关系式是________.
10、u与t成反比,且当u=6时,t=1/8,这个函数解析式为 .
11、在图中,一次函数y=x﹣2与反比例函数y=3/x的图象交点为A、B.则一次函数值小于反比例函数值时x的取值范围是
.
12、已知y与x成正比例,z与y成反比例,则z与x成__________关系,当x=1时,y=2;当y=2时,z=-2,则当x=-2时,z=
.
13、如图,反比例函数y=﹣3/x(x>0)图象经过矩形OABC边AB的中点E,交边BC于F点,
连接EF、OE、OF,则△OEF的面积是
.
14、已知三角形的面积是定值S,则三角形的高h与底a的函数关系式是,这时h是a的__________;
15、边长为4的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴,反比例函数y=2/x与y=-2/x的图象均与正方形ABCD的边相交,则图中的阴影部分的面积是
.
16、如图是本地区一种产品30天的销售图象,图是产品销售y单位:件与时间t单位:天的函数关系,图是一件产品的销售利润z(单位:元与时间t单位:天的函数关系,第27天的日销售利润是____元.
三、解答题:
17、如图,A、B两点在反比例函数y=4/x上,分别经过A、B两点向轴作垂线段,已知图中阴影部分面积S阴影=1,求图中S1+S2部分的面积?
18、在某一电路中,保持电压U(伏特)不变,电流I(安培)与电阻R(欧姆)成反比例,当电阻R=5伏特时,电流I=2安培。
(1)求I与R之间的函数关系式。
(2)当电流I=0.5安培时,求电阻R的值。
19、已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).
(1)求v关于t的函数表达式.
(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
20、我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=k/x的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
3一天24小时大棚内温度超过12℃的时间有多少小时?
21、心理学家研究发现,一般情况下,一节课
40
分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数
y随时间x(分钟)的变化规律如右图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲
19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
参考答案
一、选择题:
1、B
2、
C
3、C
4、
A
5、
C
6、C
7、A
8、C
二、填空题:
9、y=100/x
10、u=48t
11、x<﹣1
或
0<x<3
12、反比例
1
13、2.25
14、h=2S/a
反比例函数
15、8
16、875
三、解答题:
17、6
18、(1)I=U/R
(2)20欧姆
19、(1)
v=100/t;
(2)
平均每小时至少要卸货20吨.
20、(1)10小时
(2)216
(3)17.2小时
21、(1)
第
30
分钟注意力更集中.
(2)
经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
