高一数学(人教B版)-10.2.1复数的加法与减法-PPT课件(共129张PPT)
文档属性
| 名称 | 高一数学(人教B版)-10.2.1复数的加法与减法-PPT课件(共129张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-14 00:00:00 | ||
图片预览









文档简介
(共129张PPT)
复数的加法与减法
高一年级
数学
复
数
z
?
a
?
bi(a,b
?
R)
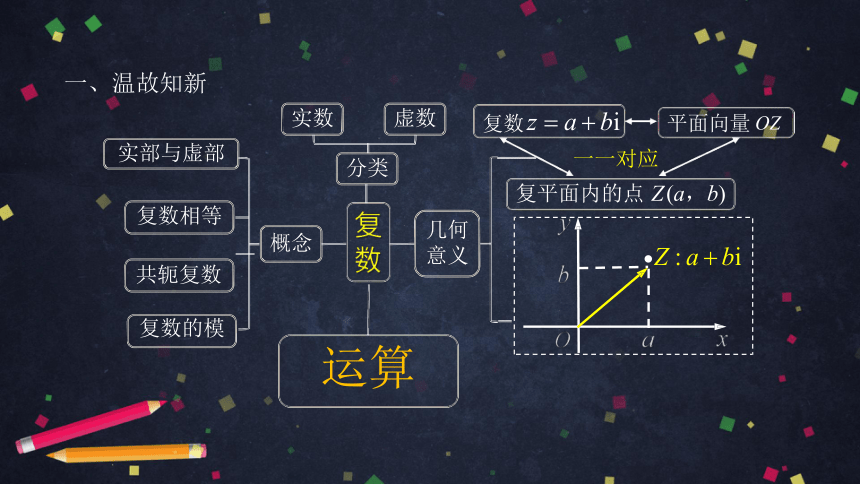
一、温故知新
复
数
概念
共轭复数
复数相等
z
?
a
?
bi(a,b
?
R)
复数的模
一、温故知新
实部与虚部
分类
实数
虚数
复数相等
概念
共轭复数
z
?
a
?
bi(a,b
?
R)
复数的模
实部与虚部
一、温故知新
复
数
概念
几何
意义
分类
实数
虚数
共轭复数
复数相等
z
?
a
?
bi(a,b
?
R)
复数的模
实部与虚部
一、温故知新
一一对应
复数z
?
a
?
bi
平面向量OZ
复平面内的点
Z
(a,b)
Z
:
a
?
bi
运算
概念
几何
意义
分类
实数
虚数
共轭复数
复数相等
复数的模
实部与虚部
一、温故知新
一一对应
复数z
?
a
?
bi
平面向量OZ
复平面内的点
Z
(a,b)
Z
:
a
?
bi
一、温故知新
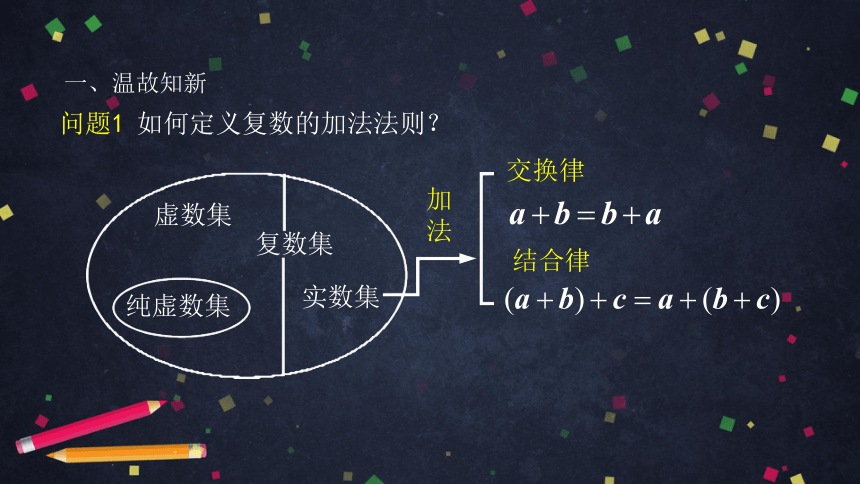
问题1
如何定义复数的加法法则?
一、温故知新
问题1
如何定义复数的加法法则?
实数集
加
法
交换律
a
?
b
?
b
?
a
结合律
(a
?
b)
?
c
?
a
?
(b
?
c)
虚数集
复数集
纯虚数集
实数集
加
法
交换律
a
?
b
?
b
?
a
结合律
(a
?
b)
?
c
?
a
?
(b
?
c)
一、温故知新
问题1
如何定义复数的加法法则?
二、探究新知—加法法则
尝试与发现
式的值应该等于多少?
(1)z1
?
z2
???.
(2)(z1
?
z2
)?
z3
?
.
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
类比多项式加法—合并同类项
二、探究新知—加法法则
尝试与发现
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
式的值应该等于多少?
z1
?
z2
?
(1?
i)
?
(2
?
2i)
?
.
二、探究新知—加法法则
类比多项式加法—合并同类项
尝试与发现
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
式的值应该等于多少?
1+2=3
z1
?
z2
?
(1?
i)
?
(2
?
2i)
?
.
二、探究新知—加法法则
尝试与发现
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
式的值应该等于多少?
1+2=3
z1
?
z2
?
(1?
i)
?
(2
?
2i)
?
.
i+(-2i)=
?
i
类比多项式加法—合并同类项
二、探究新知—加法法则
尝试与发现
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
式的值应该等于多少?
1+2=3
z1
?
z2
?
(1?
i)
?
(2
?
2i)
?
3_?_i_.
i+(-2i)=
?
i
类比多项式加法—合并同类项
二、探究新知—加法法则
尝试与发现
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
式的值应该等于多少?
(1)z1
?
z2
?
(1?
i)
?
(2
?
2i)
???3_?
i
.
(2)(z1
?
z2
)?
z3
?
(3
?
i)
?
(
?
2
?
3i)
?
.
二、探究新知—加法法则
尝试与发现
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
式的值应该等于多少?
(1)z1
?
z2
?
(1?
i)
?
(2
?
2i)
???3_?
i
.
3+(
?
2)=1
(2)(z1
?
z2
)?
z3
?
(3
?
i)
?
(
?
2
?
3i)
?
.
二、探究新知—加法法则
尝试与发现
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
式的值应该等于多少?
(1)z1
?
z2
?
(1?
i)
?
(2
?
2i)
???3_?
i
.
3+(
?
2)=1
(2)(z1
?
z2
)?
z3
?
(3
?
i)
?
(
?
2
?
3i)
?
.
-i+3i=2i
二、探究新知—加法法则
尝试与发现
式的值应该等于多少?
(1)z1
?
z2
?
(1?
i)
?
(2
?
2i)
???3_?
i
.
3+(
?
2)=1
(2)(z1
?
z2
)?
z3
?
(3
?
i)
?
(
?
2
?
3i)
?
1_+_2_i
.
-i+3i=2i
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
一般地,设z1
?
a
?
bi,z2
?
c
?
di(a,b,c,d
?R
)
称
z1
?
z2
二、探究新知—加法法则
为
z1
与z2
的和,并规定
z1
?
z2
?
(a
?
bi)
?
(c
?
di)
二、探究新知—加法法则
一般地,设z1
?
a
?
bi,z2
?
c
?
di(a,b,c,d
?R
)
称
z1
?
z2
为
z1
与z2
的和,并规定
z1
?
z2
?
(a
?
bi)
?
(c
?
di)
=(a
?
c)+(bi
?
di)
说明:
(1)运算思路:复数的加法运算类似于实数的多项式加法;
=(a
?
c)+(b
?
d
)i.
说明:
(2)运算法则:实部与实部相加,虚部与虚部相加;←文字语言
←符号语言
二、探究新知—加法法则
一般地,设z1
?
a
?
bi,z2
?
c
?
di(a,b,c,d
?R
)
称
z1
?
z2
为
z1
与z2
的和,并规定
z1
?
z2
?
(a
?
bi)
?
(c
?
di)
=(a
?
c)+(bi
?
di)
=(a
?
c)+(b
?
d
)i.
说明:
运算思路:复数的加法运算类似于实数的多项式加法;
运算法则:实部与实部相加,虚部与虚部相加;←文字语言
运算结果:两个复数的和仍然是一个复数.
←符号语言
二、探究新知—加法法则
一般地,设z1
?
a
?
bi,z2
?
c
?
di(a,b,c,d
?R
)
称
z1
?
z2
为
z1
与z2
的和,并规定
z1
?
z2
?
(a
?
bi)
?
(c
?
di)
=(a
?
c)+(bi
?
di)
二、探究新知—加法法则
思考
对任意一个实数
a
,有0
?
a
?
a
?
0
?
a
,对于任意一个复数
z
是否仍然成立?
二、探究新知—加法法则
是否仍然成立?
设
z
?
a
?
bi(a,b
?
R)
,则
0+z
?
(0
?
a)
?
bi
?
a
?
bi
?
z,
z+0
?
(a
?
0)
?
bi
?
a
?
bi
?
z.
思考
对任意一个实数
a
,有0
?
a
?
a
?
0
?
a
,对于任意一个复数
z
二、探究新知—加法法则
是否仍然成立?
设
z
?
a
?
bi(a,b
?
R)
,则
0+z
?
(0
?
a)
?
bi
?
a
?
bi
?
z,
z+0
?
(a
?
0)
?
bi
?
a
?
bi
?
z.
结论:对于任意一个复数
z
,有
0
?
z
?
z
?
0
?
z
.
思考
对任意一个实数
a
,有0
?
a
?
a
?
0
?
a
,对于任意一个复数
z
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(3)z2
?
z1
???.
(4)z1
?
(z2
?
z3
)
???.
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(3)z2
?
z1
?
.
z2
?
z1
?
(2
?
2i)
?
(1?
i)
(4)z1
?
(z2
?
z3
)
?
.
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(3)z2
?
z1
?
.
z2
?
z1
?
(2
?
2i)
?
(1?
i)
?
(2
?1)
?
(?2
?1)i
(4)z1
?
(z2
?
z3
)
?
.
z2
?
z1
?
(2
?
2i)
?
(1?
i)
?
(2
?1)
?
(?2
?1)i
?
3
?
i
2
1
(3)z
?
z
?
3
?
i
.
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(4)z1
?
(z2
?
z3
)
?
.
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
z1
?
(z2
?
z3
)
=(1
?
i)
?[(2
?
2i)
?
(
?
2
?
3i)]
1
2
3
(4)z
?
(z
?
z
)
?
.
z2
?
z1
?
(2
?
2i)
?
(1?
i)
?
(2
?1)
?
(?2
?1)i
?
3
?
i
2
1
(3)z
?
z
?
3
?
i
.
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
1
2
3
(4)z
?
(z
?
z
)
?
.
z1
?
(z2
?
z3
)
=(1
?
i)
?[(2
?
2i)
?
(
?
2
?
3i)]
?
(1?
i)
?[(2
?
2)
?
(
?
2
?
3)i]
z2
?
z1
?
(2
?
2i)
?
(1?
i)
?
(2
?1)
?
(?2
?1)i
?
3
?
i
2
1
(3)z
?
z
?
3
?
i
.
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
1
2
3
(4)z
?
(z
?
z
)
?
.
z1
?
(z2
?
z3
)
=(1
?
i)
?[(2
?
2i)
?
(
?
2
?
3i)]
?
(1?
i)
?[(2
?
2)
?
(
?
2
?
3)i]
?
(1?
i)
?
i
z2
?
z1
?
(2
?
2i)
?
(1?
i)
?
(2
?1)
?
(?2
?1)i
?
3
?
i
2
1
(3)z
?
z
?
3
?
i
.
1
2
3
z1
?
(z2
?
z3
)
=(1
?
i)
?[(2
?
2i)
?
(
?
2
?
3i)]
?
(1?
i)
?[(2
?
2)
?
(
?
2
?
3)i]
?
(1?
i)
?
i
?
1?
2i
(4)z
?
(z
?
z
)
?
1+2i
.
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
z2
?
z1
?
(2
?
2i)
?
(1?
i)
?
(2
?1)
?
(?2
?1)i
?
3
?
i
2
1
(3)z
?
z
?
3
?
i
.
(4)
z1
?
(z2
?
z3
)
?
_1_+2_i
.
对比
观察
二、探究新知—加法法则
尝试与发现
(1)z1
?
z2
?
3_?
i
.
(2)(z1
?
z2
)
?
z3
?
_1_+2_i
.
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(3)z2
?
z1
?
3_?
i
.
复数的加法
交换律
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(3)z2
?
z1
?
3_?
i
.
(4)
z1
?
(z2
?
z3
)
?
_1_+2_i
.
尝试与发现
(1)z1
?
z2
?
3_?
i
.
(2)(z1
?
z2
)
?
z3
?
_1_+2_i
.
复数的加法
交换律
结合律
二、探究新知—加法法则
(4)
z1
?
(z2
?
z3
)
?
_1_+2_i
.
尝试与发现
(1)z1
?
z2
?
3_?
i
.
(2)(z1
?
z2
)
?
z3
?
_1_+2_i
.
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(3)z2
?
z1
?
3_?
i
.
任意复数的加法
交换律?
结合律?
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(3)z2
?
z1
?
3_?
i
.
(4)
z1
?
(z2
?
z3
)
?
_1_+2_i
.
特殊
一般
尝试与发现
(1)z1
?
z2
?
3_?
i
.
(2)(z1
?
z2
)
?
z3
?
_1_+2_i
.
证明:复数的加法满足交换律.
二、探究新知—加法法则
证明:复数的加法满足交换律.
设
z1
?
a1
?
b1i,z2
=a2
?
b2i(a1,b1,
a2,
b2
?R
),
二、探究新知—加法法则
二、探究新知—加法法则
证明:复数的加法满足交换律.
设
z1
?
a1
?
b1i,z2
=a2
?
b2i(a1,b1,
a2,
b2
?R
),
Q
z1
?
z2
?
(a1
?
b1i)
?
(a2
?
b2i)=(a1
?
a2
)
?
(b1
?
b2
)i,
z2
?
z1
?
(a2
?
b2i)
?
(a1
?
b1i)=(a2
?
a1
)
?
(b2
?
b1
)i
二、探究新知—加法法则
证明:复数的加法满足交换律.
设
z1
?
a1
?
b1i,z2
=a2
?
b2i(a1,b1,
a2,
b2
?R
),
Q
z1
?
z2
?
(a1
?
b1i)
?
(a2
?
b2i)=(a1
?
a2
)
?
(b1
?
b2
)i,
z2
?
z1
?
(a2
?
b2i)
?
(a1
?
b1i)=(a2
?
a1
)
?
(b2
?
b1
)i
又
a1
?
a2
?
a2
?
a1,b1
?
b2
?
b2
?
b1,
二、探究新知—加法法则
证明:复数的加法满足交换律.
设
z1
?
a1
?
b1i,z2
=a2
?
b2i(a1,b1,
a2,
b2
?R
),
Q
z1
?
z2
?
(a1
?
b1i)
?
(a2
?
b2i)=(a1
?
a2
)
?
(b1
?
b2
)i,
z2
?
z1
?
(a2
?
b2i)
?
(a1
?
b1i)=(a2
?
a1
)
?
(b2
?
b1
)i
又
a1
?
a2
?
a2
?
a1,b1
?
b2
?
b2
?
b1,
?
z1
?
z2
?
z2
?
z1.
二、探究新知—加法法则
证明:复数的加法满足交换律.
设
z1
?
a1
?
b1i,z2
=a2
?
b2i(a1,b1,
a2,
b2
?R
),
Q
z1
?
z2
?
(a1
?
b1i)
?
(a2
?
b2i)=(a1
?
a2
)
?
(b1
?
b2
)i,
z2
?
z1
?
(a2
?
b2i)
?
(a1
?
b1i)=(a2
?
a1
)
?
(b2
?
b1
)i
又
a1
?
a2
?
a2
?
a1,b1
?
b2
?
b2
?
b1,
?
z1
?
z2
?
z2
?
z1.
请同学们独立证明:复数的加法满足结合律.
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
操作
z1
?
z2
?
1?
2i.
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
操作
1
2
z
?
z
?
1?
2i.
复数
z1
?
2
?
2i
向量
OZ1
?
(2,2)
,
1
2
x
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
y
1
Z
2
1
O
?1
?2
?3
??
操作
1
2
z
?
z
?
1?
2i.
复数
z1
?
2
?
2i
向量
OZ1
?
(2,2)
,
2
2
复数z
?
?1?
4i
向量OZ
?
(?1,?
4),
1
2
x
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
y
1
Z
2
1
O
?1
?2
?3
Z2??
操作
1
2
z
?
z
?
1?
2i.
复数
z1
?
2
?
2i
向量
OZ1
?
(2,2)
,
2
2
复数z
?
?1?
4i
向量OZ
?
(?1,?
4),
复数z1
?
z2
?
1
?
2i
向量OZ
?
(1,?
2),
1
2
x
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
y
1
Z
2
1
O
?1
?2
?3
Z2??
Z
发现
1
2
z
?
z
?
1?
2i.
复数
z1
?
2
?
2i
向量
OZ1
?
(2,2)
,
2
2
复数z
?
?1?
4i
向量OZ
?
(?1,?
4),
复数z1
?
z2
?
1
?
2i
向量OZ
?
(1,?
2),
OZ1
?
OZ2
?
(1,?
2)
?
OZ.
1
2
x
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
y
1
Z
2
1
O
?1
?2
?3
Z2??
Z
发现
OZ1
?
OZ2
?
OZ.
复数z1
?
z2
1
2
z
?
z
?
1?
2i.
复数
z1
?
2
?
2i
向量
OZ1
?
(2,2)
,
2
2
复数z
?
?1?
4i
向量OZ
?
(?1,?
4),
复数z1
?
z2
?
1
?
2i
向量OZ
?
(1,?
2),
1
2
x
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
y
1
Z
2
1
O
?1
?2
?3
2
Z
??
Z
猜想
向量OZ1
复数
z1
,
记:OZ1
?
OZ2
?
OZ,
2
2
向量OZ
复数
z
,
1
2
z
?
z
任意复数
向量OZ
.
1
2
x
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
y
1
Z
2
1
O
?1
?2
?3
2
Z
??
Z
二、探究新知—加法法则
问题2
你能由复数与向量的对应关系探究复数加法的几何意义?
二、探究新知—加法法则
问题2
你能由复数与向量的对应关系探究复数加法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R).
Z1(a,b)
二、探究新知—加法法则
问题2
你能由复数与向量的对应关系探究复数加法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R).
复数
z1
向量
OZ1
?
(a,b)
,
Z1(a,b)
Z2(c,d)
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
复数
z1
复数
z2
二、探究新知—加法法则
问题2
你能由复数与向量的对应关系探究复数加法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R).
Z1(a,b)
Z
Z2(c,d)
2
复数
z
向量OZ
?
(c,d
)
,
二、探究新知—加法法则
问题2
你能由复数与向量的对应关系探究复数加法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R).
复数
z1
向量
OZ1
?
(a,b)
,
OZ
?
OZ1
2
?
OZ2
?
(a
?
c,b
?
d),
Z1(a,b)
Z2(c,d)
z1
?
z2
?
(a
?
c)
?
(b
?
d
)i
二、探究新知—加法法则
问题2
你能由复数与向量的对应关系探究复数加法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R).
复
数
z1
复
数
z2
OZ
?
OZ1
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
?
OZ2
?
(a
?
c,b
?
d),
二、探究新知—加法法则
问题2
你能由复数与向量的对应关系探究复数加法的几何意义?
Z1(a,b)
Z2(c,d)
向量OZ
.
复数
z1
?
z2
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R).
z1
?
z2
?
(a
?
c)
?
(b
?
d
)i
复
数
z1
复
数
z2
OZ
?
OZ1
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
?
OZ2
?
(a
?
c,b
?
d),
Z1(a,b)
Z2(c,d)
复数z1
?
z2
向量
OZ
复数加法的几何意义
二、探究新知—加法法则
2
z1
?
z2
?
z1
?
z2
?
z1
?
z
由复数加法的几何意义得
1
|z
|
二、探究新知—加法法则
|z1
+z2
|
复数z1
?
z2
向量
OZ
Z1(a,b)
|z2
|
Z2(c,d)
复数加法的几何意义
二、探究新知—减法法则
问题3
如何定义复数的减法法则?
二、探究新知—减法法则
问题3
如何定义复数的减法法则?
尝试与发现
设
z1
?
5
?
8i,z2
?
5
?
3i
猜测
z2
的相反数以及
z1
?
z2
的值.
二、探究新知—减法法则
尝试与发现
设
z1
?
5
?
8i,z2
?
5
?
3i
猜测
z2
的相反数以及
z1
?
z2
的值.
猜测
z2
的相反数为?5+3i.
类比
相反数
实数
b
?
(?b)
?
0
b
的相反数为?b
复数
(a
?
bi)
?
(?a
?
bi)
?
0
a
?
bi
的相反数为?
a
?
bi
二、探究新知—减法法则
尝试与发现
设
z1
?
5
?
8i,z2
?
5
?
3i
猜测
z2
的相反数以及
z1
?
z2
的值.
猜测
z2
的相反数为?5+3i.
二、探究新知—减法法则
猜测
z2
的相反数为?5+3i.
尝试与发现
设
z1
?
5
?
8i,z2
?
5
?
3i
猜测
z2
的相反数以及
z1
?
z2
的值.
猜
测
z1
?
z2
?
z1
?
(
?
z2
)
?
(5
?
8i)
?
(
?
5
?
3i)
?
11i
1
2
?
z
?
(
?
z
)
猜
测
z1
?
z2
减法
实数
a
?
b
?
a
?
(
?
b)
复数
z1
?
z2
?
z1
?
(
?
z2
)
?
(5
?
8i)
?
(
?
5
?
3i)
?
11i
类比
二、探究新知—减法法则
尝试与发现
设
z1
?
5
?
8i,z2
?
5
?
3i
猜测
z2
的相反数以及
z1
?
z2
的值.
猜测
z2
的相反数为?5+3i.
二、探究新知—减法法则
一般地,复数z
?
a
?
bi(a,b
?
R)
的相反数记作
?z
,并规定
?z
?
?(a
?
bi)
?
?a
?
bi.
复数
z1
减去
z2的差记作
z1
?
z2
,并规定
z1
?
z2
?
z1
?
(?z2
).
二、探究新知—减法法则
一般地,如果
z1
?
a
?
bi,z2
?
c
?
di(a,b,c,d
?R
)
则
z1
?
z2
?
z1
?
(
?
z2
)
?
(a
?
bi)
?
(
?
c
?
di)
说明:
(1)运算思路:复数的减法法则—减去一个复数等于加上这个复数的相反数;
?
(a
?
c)
?
(b
?
d
)i
说明:
←符号语言
运算思路:复数的减法法则—减去一个复数等于加上这个复数的相反数;
运算法则:实部与实部相减,虚部与虚部相减;←文字语言
二、探究新知—减法法则
一般地,如果
z1
?
a
?
bi,z2
?
c
?
di(a,b,c,d
?R
)
则
z1
?
z2
?
z1
?
(
?
z2
)
?
(a
?
bi)
?
(
?
c
?
di)
运算思路:复数的减法法则—减去一个复数等于加上这个复数的相反数;
运算法则:实部与实部相减,虚部与虚部相减;←文字语言
运算结果:两个复数的差仍然是一个复数.
?
(a
?
c)
?
(b
?
d
)i
说明:
←符号语言
二、探究新知—减法法则
一般地,如果
z1
?
a
?
bi,z2
?
c
?
di(a,b,c,d
?R
)
则
z1
?
z2
?
z1
?
(
?
z2
)
?
(a
?
bi)
?
(
?
c
?
di)
二、探究新知—减法法则
练习2
设
z1
?
3
?
2i
,z2
?
5
?
i,计算下列各式的值.
(5)z1
?
z2
?
.
(6)z2
?
z1
?
.
(6)z2
?
z1
?
.
(5)z1
?
z2
?
_?_2_?
3_i
.
z1
?
z2
?
z1
?
(?z2
)
?
(3
?
2i)
?
(?5
?
i)
?
(3
?
5)
?
(2
?1)i
?
?2
?
3i.
二、探究新知—减法法则
练习2
设
z1
?
3
?
2i
,z2
?
5
?
i,计算下列各式的值.
(5)z1
?
z2
?
_?_2_?
3_i
.
z1
?
z2
?
z1
?
(?z2
)
?
(3
?
2i)
?
(?5
?
i)
?
(3
?
5)
?
(2
?1)i
?
?2
?
3i.
二、探究新知—减法法则
练习2
设
z1
?
3
?
2i
,z2
?
5
?
i,计算下列各式的值.
(6)z2
?
z1
?
2_?_3_i
.
z2
?
z1
?
(5
?
i)
?
(3
?
2i)
?
(5
?
3)
?
(
?1?
2)i
?
2
?
3i.
(5)z1
?
z2
?
_?_2_?
3_i
.
(6)z2
?
z1
?
2_?_3_i
.
复数的减法
不满足交换律
z1
?
z2
与
z2
?
z1互为相反数
二、探究新知—减法法则
练习2
设
z1
?
3
?
2i
,z2
?
5
?
i,计算下列各式的值.
二、探究新知—减法法则
问题4
探究复数减法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R)
二、探究新知—减法法则
问题4
探究复数减法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R)
复数
z1
向量
OZ1
?
(a,b)
,
O
x
y
Z1(a,b)
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
复数
z1
复数
z2
二、探究新知—减法法则
问题4
探究复数减法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R)
O
y
Z1(a,b)
x
Z2(c,d)
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
复数
z1
复数
z2
二、探究新知—减法法则
问题4
探究复数减法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R)
OZ1
?
OZ2
?
Z2
Z1
?
(a
?
c,b
?
d
)
O
y
Z1(a,b)
x
Z2(c,d)
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
复数
z1
复数
z2
二、探究新知—减法法则
问题4
探究复数减法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R)
O
y
Z1(a,b)
x
Z2(c,d)
OZ1
?
OZ2
?
Z2
Z1
?
(a
?
c,b
?
d
)
z1
?
z2
?
(a
?
c)
?
(b
?
d
)i,
复数
z1
?
z2
向量
Z2
Z1
.
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
复数
z1
复数
z2
二、探究新知—减法法则
问题4
探究复数减法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R)
O
y
Z1(a,b)
x
Z2(c,d)
OZ1
?
OZ2
?
Z2
Z1
?
(a
?
c,b
?
d
)
z1
?
z2
?
(a
?
c)
?
(b
?
d
)i,
O
Z(a?c,b?d)
y
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
复数
z1
复数
z2
二、探究新知—减法法则
问题4
探究复数减法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R)
复数
z1
?
z2
向量
Z2
Z1
=OZ
.
Z1(a,b)
x
Z2(c,d)
OZ1
?
OZ2
?
Z2
Z1
?
(a
?
c,b
?
d
)
z1
?
z2
?
(a
?
c)
?
(b
?
d
)i,OZ
=(a
?
c,b
?
d
),
二、探究新知—减法法则
复数减法的几何意义
复数z1
?
z2
向量
Z2Z1
?
OZ
O
Z1(a,b)
x
Z2(c,d)
Z(a?c,b?d)
y
二、探究新知—减法法则
2
z1
?
z2
?
z1
?
z2
?
z1
?
z
由复数减法的几何意义得
复数减法的几何意义
1
z
z2
复数z1
?
z2
向量
Z2Z1
?
OZ
O
z1
?
z2
x
Z1(a,b)
Z2(c,d)
Z(a?c,b?d)
y
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
设复数z
?
a
?
bi(a,b
?
R)
共轭复数
z
?
a
?
bi.
分
析
问
题
复数z
?
a
?
bi(a,b
?
R)
实数(b
?
0)
虚数(b
?
0)
纯虚数(a
?
0且b
?
0)
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
设复数z
?
a
?
bi(a,b
?
R)
共轭复数
z
?
a
?
bi.
分
析
问
题
复数的加法
z
?
z
??
复数的减法
z
?
z
??
复数z
?
a
?
bi(a,b
?
R)
实数(b
?
0)
虚数(b
?
0)
纯虚数(a
?
0且b
?
0)
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
设复数z
?
a
?
bi(a,b
?
R)
共轭复数
z
?
a
?
bi.
分
析
问
题
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
解:
设
z
?
a
?
bi(a,b
?
R),则
z
?
a
?
bi.
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
解:
设
z
?
a
?
bi(a,b
?
R),则
z
?
a
?
bi.
z+z
?
2a
?
R
,两个共轭复数的和为实数.
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
解:
设
z
?
a
?
bi(a,b
?
R),则
z
?
a
?
bi.
z+z
?
2a
?
R
,两个共轭复数的和为实数.
z
?
z
?
2bi
分类
讨论
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
解:
设
z
?
a
?
bi(a,b
?
R),则
z
?
a
?
bi.
z+z
?
2a
?
R
,两个共轭复数的和为实数.
z
?
z
?
2bi
讨论
z
?
z
?
2bi
分类
(1)当
b
?
0
时,z
?
z
?
0为实数.
(2)当
b
?
0
时,z
?
z
?
2bi
为纯虚数.
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
解:
设
z
?
a
?
bi(a,b
?
R),则
z
?
a
?
bi.
z+z
?
2a
?
R
,两个共轭复数的和为实数.
故命题①为真命题,命题②为假命题.
讨论
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
解:
设
z
?
a
?
bi(a,b
?
R),则
z
?
a
?
bi.
z+z
?
2a
?
R
,两个共轭复数的和为实数.
z
?
z
?
2bi
分类
(1)当
b
?
0
时,z
?
z
?
0为实数.
(2)当
b
?
0
时,z
?
z
?
2bi
为纯虚数.
四、学以致用
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
四、学以致用
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
分
析
问
题
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
四、学以致用
复数加减
混合运算
分
析
问
题
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
四、学以致用
复数的和
复数加减
混合运算
分
析
问
题
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
复数的差
四、学以致用
复数的和
复数加减
混合运算
分
析
问
题
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
四、学以致用
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
解:根据定义有
法1
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
四、学以致用
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
解:根据定义有
法1
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
?
(2
?
3)
?
(
?
5
?
7)i
?
(5
?
4i)
?
(5
?
2i)
?
(5
?
4i)
四、学以致用
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
解:根据定义有
法1
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
?
(2
?
3)
?
(
?
5
?
7)i
?
(5
?
4i)
?
(5
?
2i)
?
(5
?
4i)
?
(5
?
5)
?
(2
?
4)i
?
?2i
四、学以致用
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
解:根据定义有
法1
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
法2
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
?
(2
?
3)
?
(
?
5
?
7)i
?
(5
?
4i)
?
(5
?
2i)
?
(5
?
4i)
?
(5
?
5)
?
(2
?
4)i
?
?2i
四、学以致用
?
(2
?
3
?
5)
?
(
?
5
?
7
?
4)i
?
(2
?
3)
?
(
?
5
?
7)i
?
(5
?
4i)
?
(5
?
2i)
?
(5
?
4i)
?
(5
?
5)
?
(2
?
4)i
?
?2i
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
解:根据定义有
法1
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
法2
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
四、学以致用
?
(2
?
3
?
5)
?
(
?
5
?
7
?
4)i
?
?2i
?
(2
?
3)
?
(
?
5
?
7)i
?
(5
?
4i)
?
(5
?
2i)
?
(5
?
4i)
?
(5
?
5)
?
(2
?
4)i
?
?2i
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
解:根据定义有
法1
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
法2
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
运算法则:复数代数形式加减,只需将实部与实部相加减,虚部与
虚部相加减,复数的加(减)法可推广到多个复数相加(减)的情形.
运算顺序:从左到右计算,有括号时先算括号里面的.
运算结果:复数加减混合运算的结果仍然是一个复数.
四、学以致用
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
法2
?
(2
?
3
?
5)
?
(
?
5
?
7
?
4)i
?
?2i
法1
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
?
(5
?
2i)
?
(5
?
4i)
?
?2i
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
(2)
z
?1
?
z
?1
?
2
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
分
析
问
题
z
?
OZ,1
?
i
?
OA
?
(1,1).
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
z
?
(1?
i)
?
OZ
?
OA
?
AZ
z
?
OZ,1
?
i
?
OA
?
(1,1).
根据复数减法的几何意义得
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
|z
?
(1?
i)|
?
|OZ
?
OA|
?
|AZ|
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
z
?
OZ,1
?
i
?
OA
?
(1,1).
根据复数减法的几何意义得
|AZ|
=
2.
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
z
?
OZ,1
?
i
?
OA
?
(1,1).
根据复数减法的几何意义得
|z
?
(1?
i)|
?
|OZ
?
OA|
?
|AZ|
表示以(1,1)为圆心,2为半径的圆.
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
z
?
OZ,1
?
i
?
OA
?
(1,1).
根据复数减法的几何意义得
|AZ|
=
2.
|z
?
(1?
i)|
?
|OZ
?
OA|
?
|AZ|
(2)
z
?1
?
z
?1
?
2
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
变形
|z
?
(?1)|?|z
?1|
?
2
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(2)
z
?1
?
z
?1
?
2
z
?
OZ,?1
?
OA
?
(?1,0),1
?
OB
?
(1,0).
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(2)
z
?1
?
z
?1
?
2
变形
|z
?
(?1)|?|z
?1|
?
2
z
?
(?1)
?
AZ,z
?1
?
BZ
分
z
?
OZ,?1
?
OA
?
(?1,0),1
?
OB
?
(1,0).
析
根据复数减法的几何意义得
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(2)
z
?1
?
z
?1
?
2
变形
|z
?
(?1)|?|z
?1|
?
2
|z
?
(?1)|
?
|AZ|,|z
?1|
?
|BZ|
分
z
?
OZ,?1
?
OA
?
(?1,0),1
?
OB
?
(1,0).
析
根据复数减法的几何意义得
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(2)
z
?1
?
z
?1
?
2
变形
|z
?
(?1)|?|z
?1|
?
2
|z
?
(?1)|?|z
?1|
?
2
?
|AZ|?|BZ|
?
2,
分
z
?
OZ,?1
?
OA
?
(?1,0),1
?
OB
?
(1,0).
析
根据复数减法的几何意义得
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(2)
z
?1
?
z
?1
?
2
变形
|z
?
(?1)|?|z
?1|
?
2
分
z
?
OZ,?1
?
OA
?
(?1,0),1
?
OB
?
(1,0).
析
根据复数减法的几何意义得
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(2)
z
?1
?
z
?1
?
2
变形
|z
?
(?1)|?|z
?1|
?
2
|z
?
(?1)|?|z
?1|
?
2
?
|AZ|?|BZ|
?
2,
表示线段AB.
解:(1)表示
以1+i对应
的点
(1,1)
为圆心,
2为半径
的圆.
(2)表示以-1
和1对应的点
(-1,0)
(1,0)为端
点的线段.
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
(2)
z
?1
?
z
?1
?
2
注:z1=a+bi,z2=c+di
(a,b,c,d
?
R
)
五、课堂总结
复数的加法
复数的减法
符号
语言
z1
?
z2
?
(a
?
c)
?
(b
?
d
)i
z1
?
z2
?
(a
?
c)
?
(b
?
d
)i
文字
语言
实部与实部相加,虚部与虚部相加
实部与实部相减,虚部与虚部相减
图形
语言
几何
意义
实数的运算
复数的运算
定义新运算的原则
五、课堂总结
实数的运算
复数的运算
定义新运算的原则
类比
多项式加法
加法法则
五、课堂总结
复数的加法
从特殊
到一般
实数的运算
复数的运算
加法法则
加法几何意义
定义新运算的原则
类比
多项式加法
五、课堂总结
复数的加法
从特殊
到一般
从特殊
到一般
实数的运算
复数的运算
加法几何意义
定义新运算的原则
类比
复数的加法
多项式加法
五、课堂总结
实数减法
减法法则
复数的减法
加法法则
类比
从特殊
到一般
从特殊
到一般
实数的运算
复数的运算
加法几何意义
定义新运算的原则
类比
多项式加法
从特殊
到一般
五、课堂总结
实数减法
减法法则
类比
减法几何意义
加法法则
类比
复数的加法
复数的减法
从特殊
到一般
实数的运算
复数的运算
加法几何意义
定义新运算的原则
类比
多项式加法
五、课堂总结
实数减法
减法法则
类比
减法几何意义
加法法则
类比
数学
问题
复数的加法
复数的减法
从特殊
到一般
从特殊
到一般
复
数
概念
几何
意义
分类
实数
虚数
共轭复数
复数相等
复数的模
实部与虚部
五、课堂总结
运算
加
减
法
法
?
?
一一对应
O
x
a
b
复数z
?
a
?
bi
平面向量OZ
复平面内的点
Z
(a,b)
y
Z
:
a
?
bi
2
?
3.已知复数
z
满足
z
?
2i
?
1,求|z|的最大值与最小值.
六、课后作业
计算下列各式的值.
(1)(?3
?
2i)
?
(5
?
i)
?
(4
?
7i)
(2)(1?
i)
?
(1?
i)
?
(5
?
4i)
?
(?3
?
7i)
已知复数6
?
5i
与?3
?
4i对应的向量分别为
OA
,OB
,求
OA
+
OB
与
OA
?
OB
所对应的复数.
复数的加法与减法
高一年级
数学
复
数
z
?
a
?
bi(a,b
?
R)
一、温故知新
复
数
概念
共轭复数
复数相等
z
?
a
?
bi(a,b
?
R)
复数的模
一、温故知新
实部与虚部
分类
实数
虚数
复数相等
概念
共轭复数
z
?
a
?
bi(a,b
?
R)
复数的模
实部与虚部
一、温故知新
复
数
概念
几何
意义
分类
实数
虚数
共轭复数
复数相等
z
?
a
?
bi(a,b
?
R)
复数的模
实部与虚部
一、温故知新
一一对应
复数z
?
a
?
bi
平面向量OZ
复平面内的点
Z
(a,b)
Z
:
a
?
bi
运算
概念
几何
意义
分类
实数
虚数
共轭复数
复数相等
复数的模
实部与虚部
一、温故知新
一一对应
复数z
?
a
?
bi
平面向量OZ
复平面内的点
Z
(a,b)
Z
:
a
?
bi
一、温故知新
问题1
如何定义复数的加法法则?
一、温故知新
问题1
如何定义复数的加法法则?
实数集
加
法
交换律
a
?
b
?
b
?
a
结合律
(a
?
b)
?
c
?
a
?
(b
?
c)
虚数集
复数集
纯虚数集
实数集
加
法
交换律
a
?
b
?
b
?
a
结合律
(a
?
b)
?
c
?
a
?
(b
?
c)
一、温故知新
问题1
如何定义复数的加法法则?
二、探究新知—加法法则
尝试与发现
式的值应该等于多少?
(1)z1
?
z2
???.
(2)(z1
?
z2
)?
z3
?
.
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
类比多项式加法—合并同类项
二、探究新知—加法法则
尝试与发现
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
式的值应该等于多少?
z1
?
z2
?
(1?
i)
?
(2
?
2i)
?
.
二、探究新知—加法法则
类比多项式加法—合并同类项
尝试与发现
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
式的值应该等于多少?
1+2=3
z1
?
z2
?
(1?
i)
?
(2
?
2i)
?
.
二、探究新知—加法法则
尝试与发现
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
式的值应该等于多少?
1+2=3
z1
?
z2
?
(1?
i)
?
(2
?
2i)
?
.
i+(-2i)=
?
i
类比多项式加法—合并同类项
二、探究新知—加法法则
尝试与发现
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
式的值应该等于多少?
1+2=3
z1
?
z2
?
(1?
i)
?
(2
?
2i)
?
3_?_i_.
i+(-2i)=
?
i
类比多项式加法—合并同类项
二、探究新知—加法法则
尝试与发现
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
式的值应该等于多少?
(1)z1
?
z2
?
(1?
i)
?
(2
?
2i)
???3_?
i
.
(2)(z1
?
z2
)?
z3
?
(3
?
i)
?
(
?
2
?
3i)
?
.
二、探究新知—加法法则
尝试与发现
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
式的值应该等于多少?
(1)z1
?
z2
?
(1?
i)
?
(2
?
2i)
???3_?
i
.
3+(
?
2)=1
(2)(z1
?
z2
)?
z3
?
(3
?
i)
?
(
?
2
?
3i)
?
.
二、探究新知—加法法则
尝试与发现
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
式的值应该等于多少?
(1)z1
?
z2
?
(1?
i)
?
(2
?
2i)
???3_?
i
.
3+(
?
2)=1
(2)(z1
?
z2
)?
z3
?
(3
?
i)
?
(
?
2
?
3i)
?
.
-i+3i=2i
二、探究新知—加法法则
尝试与发现
式的值应该等于多少?
(1)z1
?
z2
?
(1?
i)
?
(2
?
2i)
???3_?
i
.
3+(
?
2)=1
(2)(z1
?
z2
)?
z3
?
(3
?
i)
?
(
?
2
?
3i)
?
1_+_2_i
.
-i+3i=2i
设z1
?
1?
i,z2
?
2
?
2i,z3
?
?2
?
3i
你认为下列各
一般地,设z1
?
a
?
bi,z2
?
c
?
di(a,b,c,d
?R
)
称
z1
?
z2
二、探究新知—加法法则
为
z1
与z2
的和,并规定
z1
?
z2
?
(a
?
bi)
?
(c
?
di)
二、探究新知—加法法则
一般地,设z1
?
a
?
bi,z2
?
c
?
di(a,b,c,d
?R
)
称
z1
?
z2
为
z1
与z2
的和,并规定
z1
?
z2
?
(a
?
bi)
?
(c
?
di)
=(a
?
c)+(bi
?
di)
说明:
(1)运算思路:复数的加法运算类似于实数的多项式加法;
=(a
?
c)+(b
?
d
)i.
说明:
(2)运算法则:实部与实部相加,虚部与虚部相加;←文字语言
←符号语言
二、探究新知—加法法则
一般地,设z1
?
a
?
bi,z2
?
c
?
di(a,b,c,d
?R
)
称
z1
?
z2
为
z1
与z2
的和,并规定
z1
?
z2
?
(a
?
bi)
?
(c
?
di)
=(a
?
c)+(bi
?
di)
=(a
?
c)+(b
?
d
)i.
说明:
运算思路:复数的加法运算类似于实数的多项式加法;
运算法则:实部与实部相加,虚部与虚部相加;←文字语言
运算结果:两个复数的和仍然是一个复数.
←符号语言
二、探究新知—加法法则
一般地,设z1
?
a
?
bi,z2
?
c
?
di(a,b,c,d
?R
)
称
z1
?
z2
为
z1
与z2
的和,并规定
z1
?
z2
?
(a
?
bi)
?
(c
?
di)
=(a
?
c)+(bi
?
di)
二、探究新知—加法法则
思考
对任意一个实数
a
,有0
?
a
?
a
?
0
?
a
,对于任意一个复数
z
是否仍然成立?
二、探究新知—加法法则
是否仍然成立?
设
z
?
a
?
bi(a,b
?
R)
,则
0+z
?
(0
?
a)
?
bi
?
a
?
bi
?
z,
z+0
?
(a
?
0)
?
bi
?
a
?
bi
?
z.
思考
对任意一个实数
a
,有0
?
a
?
a
?
0
?
a
,对于任意一个复数
z
二、探究新知—加法法则
是否仍然成立?
设
z
?
a
?
bi(a,b
?
R)
,则
0+z
?
(0
?
a)
?
bi
?
a
?
bi
?
z,
z+0
?
(a
?
0)
?
bi
?
a
?
bi
?
z.
结论:对于任意一个复数
z
,有
0
?
z
?
z
?
0
?
z
.
思考
对任意一个实数
a
,有0
?
a
?
a
?
0
?
a
,对于任意一个复数
z
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(3)z2
?
z1
???.
(4)z1
?
(z2
?
z3
)
???.
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(3)z2
?
z1
?
.
z2
?
z1
?
(2
?
2i)
?
(1?
i)
(4)z1
?
(z2
?
z3
)
?
.
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(3)z2
?
z1
?
.
z2
?
z1
?
(2
?
2i)
?
(1?
i)
?
(2
?1)
?
(?2
?1)i
(4)z1
?
(z2
?
z3
)
?
.
z2
?
z1
?
(2
?
2i)
?
(1?
i)
?
(2
?1)
?
(?2
?1)i
?
3
?
i
2
1
(3)z
?
z
?
3
?
i
.
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(4)z1
?
(z2
?
z3
)
?
.
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
z1
?
(z2
?
z3
)
=(1
?
i)
?[(2
?
2i)
?
(
?
2
?
3i)]
1
2
3
(4)z
?
(z
?
z
)
?
.
z2
?
z1
?
(2
?
2i)
?
(1?
i)
?
(2
?1)
?
(?2
?1)i
?
3
?
i
2
1
(3)z
?
z
?
3
?
i
.
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
1
2
3
(4)z
?
(z
?
z
)
?
.
z1
?
(z2
?
z3
)
=(1
?
i)
?[(2
?
2i)
?
(
?
2
?
3i)]
?
(1?
i)
?[(2
?
2)
?
(
?
2
?
3)i]
z2
?
z1
?
(2
?
2i)
?
(1?
i)
?
(2
?1)
?
(?2
?1)i
?
3
?
i
2
1
(3)z
?
z
?
3
?
i
.
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
1
2
3
(4)z
?
(z
?
z
)
?
.
z1
?
(z2
?
z3
)
=(1
?
i)
?[(2
?
2i)
?
(
?
2
?
3i)]
?
(1?
i)
?[(2
?
2)
?
(
?
2
?
3)i]
?
(1?
i)
?
i
z2
?
z1
?
(2
?
2i)
?
(1?
i)
?
(2
?1)
?
(?2
?1)i
?
3
?
i
2
1
(3)z
?
z
?
3
?
i
.
1
2
3
z1
?
(z2
?
z3
)
=(1
?
i)
?[(2
?
2i)
?
(
?
2
?
3i)]
?
(1?
i)
?[(2
?
2)
?
(
?
2
?
3)i]
?
(1?
i)
?
i
?
1?
2i
(4)z
?
(z
?
z
)
?
1+2i
.
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
z2
?
z1
?
(2
?
2i)
?
(1?
i)
?
(2
?1)
?
(?2
?1)i
?
3
?
i
2
1
(3)z
?
z
?
3
?
i
.
(4)
z1
?
(z2
?
z3
)
?
_1_+2_i
.
对比
观察
二、探究新知—加法法则
尝试与发现
(1)z1
?
z2
?
3_?
i
.
(2)(z1
?
z2
)
?
z3
?
_1_+2_i
.
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(3)z2
?
z1
?
3_?
i
.
复数的加法
交换律
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(3)z2
?
z1
?
3_?
i
.
(4)
z1
?
(z2
?
z3
)
?
_1_+2_i
.
尝试与发现
(1)z1
?
z2
?
3_?
i
.
(2)(z1
?
z2
)
?
z3
?
_1_+2_i
.
复数的加法
交换律
结合律
二、探究新知—加法法则
(4)
z1
?
(z2
?
z3
)
?
_1_+2_i
.
尝试与发现
(1)z1
?
z2
?
3_?
i
.
(2)(z1
?
z2
)
?
z3
?
_1_+2_i
.
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(3)z2
?
z1
?
3_?
i
.
任意复数的加法
交换律?
结合律?
二、探究新知—加法法则
练习1
设
z1
=1?
i
,z2
=2
?
2i
,z3
=
?
2+3i,计算下列各式的值.
(3)z2
?
z1
?
3_?
i
.
(4)
z1
?
(z2
?
z3
)
?
_1_+2_i
.
特殊
一般
尝试与发现
(1)z1
?
z2
?
3_?
i
.
(2)(z1
?
z2
)
?
z3
?
_1_+2_i
.
证明:复数的加法满足交换律.
二、探究新知—加法法则
证明:复数的加法满足交换律.
设
z1
?
a1
?
b1i,z2
=a2
?
b2i(a1,b1,
a2,
b2
?R
),
二、探究新知—加法法则
二、探究新知—加法法则
证明:复数的加法满足交换律.
设
z1
?
a1
?
b1i,z2
=a2
?
b2i(a1,b1,
a2,
b2
?R
),
Q
z1
?
z2
?
(a1
?
b1i)
?
(a2
?
b2i)=(a1
?
a2
)
?
(b1
?
b2
)i,
z2
?
z1
?
(a2
?
b2i)
?
(a1
?
b1i)=(a2
?
a1
)
?
(b2
?
b1
)i
二、探究新知—加法法则
证明:复数的加法满足交换律.
设
z1
?
a1
?
b1i,z2
=a2
?
b2i(a1,b1,
a2,
b2
?R
),
Q
z1
?
z2
?
(a1
?
b1i)
?
(a2
?
b2i)=(a1
?
a2
)
?
(b1
?
b2
)i,
z2
?
z1
?
(a2
?
b2i)
?
(a1
?
b1i)=(a2
?
a1
)
?
(b2
?
b1
)i
又
a1
?
a2
?
a2
?
a1,b1
?
b2
?
b2
?
b1,
二、探究新知—加法法则
证明:复数的加法满足交换律.
设
z1
?
a1
?
b1i,z2
=a2
?
b2i(a1,b1,
a2,
b2
?R
),
Q
z1
?
z2
?
(a1
?
b1i)
?
(a2
?
b2i)=(a1
?
a2
)
?
(b1
?
b2
)i,
z2
?
z1
?
(a2
?
b2i)
?
(a1
?
b1i)=(a2
?
a1
)
?
(b2
?
b1
)i
又
a1
?
a2
?
a2
?
a1,b1
?
b2
?
b2
?
b1,
?
z1
?
z2
?
z2
?
z1.
二、探究新知—加法法则
证明:复数的加法满足交换律.
设
z1
?
a1
?
b1i,z2
=a2
?
b2i(a1,b1,
a2,
b2
?R
),
Q
z1
?
z2
?
(a1
?
b1i)
?
(a2
?
b2i)=(a1
?
a2
)
?
(b1
?
b2
)i,
z2
?
z1
?
(a2
?
b2i)
?
(a1
?
b1i)=(a2
?
a1
)
?
(b2
?
b1
)i
又
a1
?
a2
?
a2
?
a1,b1
?
b2
?
b2
?
b1,
?
z1
?
z2
?
z2
?
z1.
请同学们独立证明:复数的加法满足结合律.
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
操作
z1
?
z2
?
1?
2i.
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
操作
1
2
z
?
z
?
1?
2i.
复数
z1
?
2
?
2i
向量
OZ1
?
(2,2)
,
1
2
x
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
y
1
Z
2
1
O
?1
?2
?3
??
操作
1
2
z
?
z
?
1?
2i.
复数
z1
?
2
?
2i
向量
OZ1
?
(2,2)
,
2
2
复数z
?
?1?
4i
向量OZ
?
(?1,?
4),
1
2
x
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
y
1
Z
2
1
O
?1
?2
?3
Z2??
操作
1
2
z
?
z
?
1?
2i.
复数
z1
?
2
?
2i
向量
OZ1
?
(2,2)
,
2
2
复数z
?
?1?
4i
向量OZ
?
(?1,?
4),
复数z1
?
z2
?
1
?
2i
向量OZ
?
(1,?
2),
1
2
x
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
y
1
Z
2
1
O
?1
?2
?3
Z2??
Z
发现
1
2
z
?
z
?
1?
2i.
复数
z1
?
2
?
2i
向量
OZ1
?
(2,2)
,
2
2
复数z
?
?1?
4i
向量OZ
?
(?1,?
4),
复数z1
?
z2
?
1
?
2i
向量OZ
?
(1,?
2),
OZ1
?
OZ2
?
(1,?
2)
?
OZ.
1
2
x
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
y
1
Z
2
1
O
?1
?2
?3
Z2??
Z
发现
OZ1
?
OZ2
?
OZ.
复数z1
?
z2
1
2
z
?
z
?
1?
2i.
复数
z1
?
2
?
2i
向量
OZ1
?
(2,2)
,
2
2
复数z
?
?1?
4i
向量OZ
?
(?1,?
4),
复数z1
?
z2
?
1
?
2i
向量OZ
?
(1,?
2),
1
2
x
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
y
1
Z
2
1
O
?1
?2
?3
2
Z
??
Z
猜想
向量OZ1
复数
z1
,
记:OZ1
?
OZ2
?
OZ,
2
2
向量OZ
复数
z
,
1
2
z
?
z
任意复数
向量OZ
.
1
2
x
二、探究新知—加法法则
设z1
?
2
?
2i
,z2
?
?1?
4i
,求出
z1
?
z2
,并在复平面内分别作
出
z1
,z2
,z1
?
z2
所对应的向量,猜想并归纳复数加法的几何意义.
y
1
Z
2
1
O
?1
?2
?3
2
Z
??
Z
二、探究新知—加法法则
问题2
你能由复数与向量的对应关系探究复数加法的几何意义?
二、探究新知—加法法则
问题2
你能由复数与向量的对应关系探究复数加法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R).
Z1(a,b)
二、探究新知—加法法则
问题2
你能由复数与向量的对应关系探究复数加法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R).
复数
z1
向量
OZ1
?
(a,b)
,
Z1(a,b)
Z2(c,d)
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
复数
z1
复数
z2
二、探究新知—加法法则
问题2
你能由复数与向量的对应关系探究复数加法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R).
Z1(a,b)
Z
Z2(c,d)
2
复数
z
向量OZ
?
(c,d
)
,
二、探究新知—加法法则
问题2
你能由复数与向量的对应关系探究复数加法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R).
复数
z1
向量
OZ1
?
(a,b)
,
OZ
?
OZ1
2
?
OZ2
?
(a
?
c,b
?
d),
Z1(a,b)
Z2(c,d)
z1
?
z2
?
(a
?
c)
?
(b
?
d
)i
二、探究新知—加法法则
问题2
你能由复数与向量的对应关系探究复数加法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R).
复
数
z1
复
数
z2
OZ
?
OZ1
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
?
OZ2
?
(a
?
c,b
?
d),
二、探究新知—加法法则
问题2
你能由复数与向量的对应关系探究复数加法的几何意义?
Z1(a,b)
Z2(c,d)
向量OZ
.
复数
z1
?
z2
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R).
z1
?
z2
?
(a
?
c)
?
(b
?
d
)i
复
数
z1
复
数
z2
OZ
?
OZ1
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
?
OZ2
?
(a
?
c,b
?
d),
Z1(a,b)
Z2(c,d)
复数z1
?
z2
向量
OZ
复数加法的几何意义
二、探究新知—加法法则
2
z1
?
z2
?
z1
?
z2
?
z1
?
z
由复数加法的几何意义得
1
|z
|
二、探究新知—加法法则
|z1
+z2
|
复数z1
?
z2
向量
OZ
Z1(a,b)
|z2
|
Z2(c,d)
复数加法的几何意义
二、探究新知—减法法则
问题3
如何定义复数的减法法则?
二、探究新知—减法法则
问题3
如何定义复数的减法法则?
尝试与发现
设
z1
?
5
?
8i,z2
?
5
?
3i
猜测
z2
的相反数以及
z1
?
z2
的值.
二、探究新知—减法法则
尝试与发现
设
z1
?
5
?
8i,z2
?
5
?
3i
猜测
z2
的相反数以及
z1
?
z2
的值.
猜测
z2
的相反数为?5+3i.
类比
相反数
实数
b
?
(?b)
?
0
b
的相反数为?b
复数
(a
?
bi)
?
(?a
?
bi)
?
0
a
?
bi
的相反数为?
a
?
bi
二、探究新知—减法法则
尝试与发现
设
z1
?
5
?
8i,z2
?
5
?
3i
猜测
z2
的相反数以及
z1
?
z2
的值.
猜测
z2
的相反数为?5+3i.
二、探究新知—减法法则
猜测
z2
的相反数为?5+3i.
尝试与发现
设
z1
?
5
?
8i,z2
?
5
?
3i
猜测
z2
的相反数以及
z1
?
z2
的值.
猜
测
z1
?
z2
?
z1
?
(
?
z2
)
?
(5
?
8i)
?
(
?
5
?
3i)
?
11i
1
2
?
z
?
(
?
z
)
猜
测
z1
?
z2
减法
实数
a
?
b
?
a
?
(
?
b)
复数
z1
?
z2
?
z1
?
(
?
z2
)
?
(5
?
8i)
?
(
?
5
?
3i)
?
11i
类比
二、探究新知—减法法则
尝试与发现
设
z1
?
5
?
8i,z2
?
5
?
3i
猜测
z2
的相反数以及
z1
?
z2
的值.
猜测
z2
的相反数为?5+3i.
二、探究新知—减法法则
一般地,复数z
?
a
?
bi(a,b
?
R)
的相反数记作
?z
,并规定
?z
?
?(a
?
bi)
?
?a
?
bi.
复数
z1
减去
z2的差记作
z1
?
z2
,并规定
z1
?
z2
?
z1
?
(?z2
).
二、探究新知—减法法则
一般地,如果
z1
?
a
?
bi,z2
?
c
?
di(a,b,c,d
?R
)
则
z1
?
z2
?
z1
?
(
?
z2
)
?
(a
?
bi)
?
(
?
c
?
di)
说明:
(1)运算思路:复数的减法法则—减去一个复数等于加上这个复数的相反数;
?
(a
?
c)
?
(b
?
d
)i
说明:
←符号语言
运算思路:复数的减法法则—减去一个复数等于加上这个复数的相反数;
运算法则:实部与实部相减,虚部与虚部相减;←文字语言
二、探究新知—减法法则
一般地,如果
z1
?
a
?
bi,z2
?
c
?
di(a,b,c,d
?R
)
则
z1
?
z2
?
z1
?
(
?
z2
)
?
(a
?
bi)
?
(
?
c
?
di)
运算思路:复数的减法法则—减去一个复数等于加上这个复数的相反数;
运算法则:实部与实部相减,虚部与虚部相减;←文字语言
运算结果:两个复数的差仍然是一个复数.
?
(a
?
c)
?
(b
?
d
)i
说明:
←符号语言
二、探究新知—减法法则
一般地,如果
z1
?
a
?
bi,z2
?
c
?
di(a,b,c,d
?R
)
则
z1
?
z2
?
z1
?
(
?
z2
)
?
(a
?
bi)
?
(
?
c
?
di)
二、探究新知—减法法则
练习2
设
z1
?
3
?
2i
,z2
?
5
?
i,计算下列各式的值.
(5)z1
?
z2
?
.
(6)z2
?
z1
?
.
(6)z2
?
z1
?
.
(5)z1
?
z2
?
_?_2_?
3_i
.
z1
?
z2
?
z1
?
(?z2
)
?
(3
?
2i)
?
(?5
?
i)
?
(3
?
5)
?
(2
?1)i
?
?2
?
3i.
二、探究新知—减法法则
练习2
设
z1
?
3
?
2i
,z2
?
5
?
i,计算下列各式的值.
(5)z1
?
z2
?
_?_2_?
3_i
.
z1
?
z2
?
z1
?
(?z2
)
?
(3
?
2i)
?
(?5
?
i)
?
(3
?
5)
?
(2
?1)i
?
?2
?
3i.
二、探究新知—减法法则
练习2
设
z1
?
3
?
2i
,z2
?
5
?
i,计算下列各式的值.
(6)z2
?
z1
?
2_?_3_i
.
z2
?
z1
?
(5
?
i)
?
(3
?
2i)
?
(5
?
3)
?
(
?1?
2)i
?
2
?
3i.
(5)z1
?
z2
?
_?_2_?
3_i
.
(6)z2
?
z1
?
2_?_3_i
.
复数的减法
不满足交换律
z1
?
z2
与
z2
?
z1互为相反数
二、探究新知—减法法则
练习2
设
z1
?
3
?
2i
,z2
?
5
?
i,计算下列各式的值.
二、探究新知—减法法则
问题4
探究复数减法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R)
二、探究新知—减法法则
问题4
探究复数减法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R)
复数
z1
向量
OZ1
?
(a,b)
,
O
x
y
Z1(a,b)
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
复数
z1
复数
z2
二、探究新知—减法法则
问题4
探究复数减法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R)
O
y
Z1(a,b)
x
Z2(c,d)
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
复数
z1
复数
z2
二、探究新知—减法法则
问题4
探究复数减法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R)
OZ1
?
OZ2
?
Z2
Z1
?
(a
?
c,b
?
d
)
O
y
Z1(a,b)
x
Z2(c,d)
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
复数
z1
复数
z2
二、探究新知—减法法则
问题4
探究复数减法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R)
O
y
Z1(a,b)
x
Z2(c,d)
OZ1
?
OZ2
?
Z2
Z1
?
(a
?
c,b
?
d
)
z1
?
z2
?
(a
?
c)
?
(b
?
d
)i,
复数
z1
?
z2
向量
Z2
Z1
.
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
复数
z1
复数
z2
二、探究新知—减法法则
问题4
探究复数减法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R)
O
y
Z1(a,b)
x
Z2(c,d)
OZ1
?
OZ2
?
Z2
Z1
?
(a
?
c,b
?
d
)
z1
?
z2
?
(a
?
c)
?
(b
?
d
)i,
O
Z(a?c,b?d)
y
向量
OZ1
?
(a,b)
,
向量OZ2
?
(c,d
)
,
复数
z1
复数
z2
二、探究新知—减法法则
问题4
探究复数减法的几何意义?
设z1
?
a
?
bi,z2
?
c
?
di
(a,b,c,d
?R)
复数
z1
?
z2
向量
Z2
Z1
=OZ
.
Z1(a,b)
x
Z2(c,d)
OZ1
?
OZ2
?
Z2
Z1
?
(a
?
c,b
?
d
)
z1
?
z2
?
(a
?
c)
?
(b
?
d
)i,OZ
=(a
?
c,b
?
d
),
二、探究新知—减法法则
复数减法的几何意义
复数z1
?
z2
向量
Z2Z1
?
OZ
O
Z1(a,b)
x
Z2(c,d)
Z(a?c,b?d)
y
二、探究新知—减法法则
2
z1
?
z2
?
z1
?
z2
?
z1
?
z
由复数减法的几何意义得
复数减法的几何意义
1
z
z2
复数z1
?
z2
向量
Z2Z1
?
OZ
O
z1
?
z2
x
Z1(a,b)
Z2(c,d)
Z(a?c,b?d)
y
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
设复数z
?
a
?
bi(a,b
?
R)
共轭复数
z
?
a
?
bi.
分
析
问
题
复数z
?
a
?
bi(a,b
?
R)
实数(b
?
0)
虚数(b
?
0)
纯虚数(a
?
0且b
?
0)
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
设复数z
?
a
?
bi(a,b
?
R)
共轭复数
z
?
a
?
bi.
分
析
问
题
复数的加法
z
?
z
??
复数的减法
z
?
z
??
复数z
?
a
?
bi(a,b
?
R)
实数(b
?
0)
虚数(b
?
0)
纯虚数(a
?
0且b
?
0)
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
设复数z
?
a
?
bi(a,b
?
R)
共轭复数
z
?
a
?
bi.
分
析
问
题
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
解:
设
z
?
a
?
bi(a,b
?
R),则
z
?
a
?
bi.
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
解:
设
z
?
a
?
bi(a,b
?
R),则
z
?
a
?
bi.
z+z
?
2a
?
R
,两个共轭复数的和为实数.
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
解:
设
z
?
a
?
bi(a,b
?
R),则
z
?
a
?
bi.
z+z
?
2a
?
R
,两个共轭复数的和为实数.
z
?
z
?
2bi
分类
讨论
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
解:
设
z
?
a
?
bi(a,b
?
R),则
z
?
a
?
bi.
z+z
?
2a
?
R
,两个共轭复数的和为实数.
z
?
z
?
2bi
讨论
z
?
z
?
2bi
分类
(1)当
b
?
0
时,z
?
z
?
0为实数.
(2)当
b
?
0
时,z
?
z
?
2bi
为纯虚数.
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
解:
设
z
?
a
?
bi(a,b
?
R),则
z
?
a
?
bi.
z+z
?
2a
?
R
,两个共轭复数的和为实数.
故命题①为真命题,命题②为假命题.
讨论
三、理解辨析
已知命题①两个共轭复数的和一定是实数;②两个共轭复
数的差一定是纯虚数.判断以上命题的真假,并说明理由.
解:
设
z
?
a
?
bi(a,b
?
R),则
z
?
a
?
bi.
z+z
?
2a
?
R
,两个共轭复数的和为实数.
z
?
z
?
2bi
分类
(1)当
b
?
0
时,z
?
z
?
0为实数.
(2)当
b
?
0
时,z
?
z
?
2bi
为纯虚数.
四、学以致用
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
四、学以致用
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
分
析
问
题
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
四、学以致用
复数加减
混合运算
分
析
问
题
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
四、学以致用
复数的和
复数加减
混合运算
分
析
问
题
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
复数的差
四、学以致用
复数的和
复数加减
混合运算
分
析
问
题
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
四、学以致用
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
解:根据定义有
法1
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
四、学以致用
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
解:根据定义有
法1
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
?
(2
?
3)
?
(
?
5
?
7)i
?
(5
?
4i)
?
(5
?
2i)
?
(5
?
4i)
四、学以致用
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
解:根据定义有
法1
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
?
(2
?
3)
?
(
?
5
?
7)i
?
(5
?
4i)
?
(5
?
2i)
?
(5
?
4i)
?
(5
?
5)
?
(2
?
4)i
?
?2i
四、学以致用
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
解:根据定义有
法1
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
法2
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
?
(2
?
3)
?
(
?
5
?
7)i
?
(5
?
4i)
?
(5
?
2i)
?
(5
?
4i)
?
(5
?
5)
?
(2
?
4)i
?
?2i
四、学以致用
?
(2
?
3
?
5)
?
(
?
5
?
7
?
4)i
?
(2
?
3)
?
(
?
5
?
7)i
?
(5
?
4i)
?
(5
?
2i)
?
(5
?
4i)
?
(5
?
5)
?
(2
?
4)i
?
?2i
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
解:根据定义有
法1
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
法2
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
四、学以致用
?
(2
?
3
?
5)
?
(
?
5
?
7
?
4)i
?
?2i
?
(2
?
3)
?
(
?
5
?
7)i
?
(5
?
4i)
?
(5
?
2i)
?
(5
?
4i)
?
(5
?
5)
?
(2
?
4)i
?
?2i
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
解:根据定义有
法1
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
法2
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
运算法则:复数代数形式加减,只需将实部与实部相加减,虚部与
虚部相加减,复数的加(减)法可推广到多个复数相加(减)的情形.
运算顺序:从左到右计算,有括号时先算括号里面的.
运算结果:复数加减混合运算的结果仍然是一个复数.
四、学以致用
例1
计算(2
?
5i)
?
(3
?
7i)
?
(5
?
4i).
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
法2
?
(2
?
3
?
5)
?
(
?
5
?
7
?
4)i
?
?2i
法1
(2
?
5i)
?
(3
?
7i)
?
(5
?
4i)
?
(5
?
2i)
?
(5
?
4i)
?
?2i
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
(2)
z
?1
?
z
?1
?
2
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
分
析
问
题
z
?
OZ,1
?
i
?
OA
?
(1,1).
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
z
?
(1?
i)
?
OZ
?
OA
?
AZ
z
?
OZ,1
?
i
?
OA
?
(1,1).
根据复数减法的几何意义得
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
|z
?
(1?
i)|
?
|OZ
?
OA|
?
|AZ|
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
z
?
OZ,1
?
i
?
OA
?
(1,1).
根据复数减法的几何意义得
|AZ|
=
2.
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
z
?
OZ,1
?
i
?
OA
?
(1,1).
根据复数减法的几何意义得
|z
?
(1?
i)|
?
|OZ
?
OA|
?
|AZ|
表示以(1,1)为圆心,2为半径的圆.
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
z
?
OZ,1
?
i
?
OA
?
(1,1).
根据复数减法的几何意义得
|AZ|
=
2.
|z
?
(1?
i)|
?
|OZ
?
OA|
?
|AZ|
(2)
z
?1
?
z
?1
?
2
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
变形
|z
?
(?1)|?|z
?1|
?
2
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(2)
z
?1
?
z
?1
?
2
z
?
OZ,?1
?
OA
?
(?1,0),1
?
OB
?
(1,0).
分
析
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(2)
z
?1
?
z
?1
?
2
变形
|z
?
(?1)|?|z
?1|
?
2
z
?
(?1)
?
AZ,z
?1
?
BZ
分
z
?
OZ,?1
?
OA
?
(?1,0),1
?
OB
?
(1,0).
析
根据复数减法的几何意义得
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(2)
z
?1
?
z
?1
?
2
变形
|z
?
(?1)|?|z
?1|
?
2
|z
?
(?1)|
?
|AZ|,|z
?1|
?
|BZ|
分
z
?
OZ,?1
?
OA
?
(?1,0),1
?
OB
?
(1,0).
析
根据复数减法的几何意义得
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(2)
z
?1
?
z
?1
?
2
变形
|z
?
(?1)|?|z
?1|
?
2
|z
?
(?1)|?|z
?1|
?
2
?
|AZ|?|BZ|
?
2,
分
z
?
OZ,?1
?
OA
?
(?1,0),1
?
OB
?
(1,0).
析
根据复数减法的几何意义得
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(2)
z
?1
?
z
?1
?
2
变形
|z
?
(?1)|?|z
?1|
?
2
分
z
?
OZ,?1
?
OA
?
(?1,0),1
?
OB
?
(1,0).
析
根据复数减法的几何意义得
问
题
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(2)
z
?1
?
z
?1
?
2
变形
|z
?
(?1)|?|z
?1|
?
2
|z
?
(?1)|?|z
?1|
?
2
?
|AZ|?|BZ|
?
2,
表示线段AB.
解:(1)表示
以1+i对应
的点
(1,1)
为圆心,
2为半径
的圆.
(2)表示以-1
和1对应的点
(-1,0)
(1,0)为端
点的线段.
例2
根据
z1
?
z2
的几何意义讨论下列各式的几何意义.
四、学以致用
(1)
z
?
(1?
i)
?
2
(2)
z
?1
?
z
?1
?
2
注:z1=a+bi,z2=c+di
(a,b,c,d
?
R
)
五、课堂总结
复数的加法
复数的减法
符号
语言
z1
?
z2
?
(a
?
c)
?
(b
?
d
)i
z1
?
z2
?
(a
?
c)
?
(b
?
d
)i
文字
语言
实部与实部相加,虚部与虚部相加
实部与实部相减,虚部与虚部相减
图形
语言
几何
意义
实数的运算
复数的运算
定义新运算的原则
五、课堂总结
实数的运算
复数的运算
定义新运算的原则
类比
多项式加法
加法法则
五、课堂总结
复数的加法
从特殊
到一般
实数的运算
复数的运算
加法法则
加法几何意义
定义新运算的原则
类比
多项式加法
五、课堂总结
复数的加法
从特殊
到一般
从特殊
到一般
实数的运算
复数的运算
加法几何意义
定义新运算的原则
类比
复数的加法
多项式加法
五、课堂总结
实数减法
减法法则
复数的减法
加法法则
类比
从特殊
到一般
从特殊
到一般
实数的运算
复数的运算
加法几何意义
定义新运算的原则
类比
多项式加法
从特殊
到一般
五、课堂总结
实数减法
减法法则
类比
减法几何意义
加法法则
类比
复数的加法
复数的减法
从特殊
到一般
实数的运算
复数的运算
加法几何意义
定义新运算的原则
类比
多项式加法
五、课堂总结
实数减法
减法法则
类比
减法几何意义
加法法则
类比
数学
问题
复数的加法
复数的减法
从特殊
到一般
从特殊
到一般
复
数
概念
几何
意义
分类
实数
虚数
共轭复数
复数相等
复数的模
实部与虚部
五、课堂总结
运算
加
减
法
法
?
?
一一对应
O
x
a
b
复数z
?
a
?
bi
平面向量OZ
复平面内的点
Z
(a,b)
y
Z
:
a
?
bi
2
?
3.已知复数
z
满足
z
?
2i
?
1,求|z|的最大值与最小值.
六、课后作业
计算下列各式的值.
(1)(?3
?
2i)
?
(5
?
i)
?
(4
?
7i)
(2)(1?
i)
?
(1?
i)
?
(5
?
4i)
?
(?3
?
7i)
已知复数6
?
5i
与?3
?
4i对应的向量分别为
OA
,OB
,求
OA
+
OB
与
OA
?
OB
所对应的复数.
