9.3 一元一次不等式组课件(共20张PPT)
文档属性
| 名称 | 9.3 一元一次不等式组课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 09:00:44 | ||
图片预览







文档简介
(共20张PPT)
人教版
七年级数学下
9.3一元一次不等式组
教学目标
1.通过具体操作,在解一元一次不等式组的过程中形成正确的解不等
式组的思路与方法;(重点、难点)
2.掌握在数轴上正确表示一元一次不等式组的解集的方法.(重点)
回顾旧知
1.怎样解一元一次不等式?
解一元一次不等式,根据不等式的性质,将不等式逐步化
为x>a(或x一般步骤为:
去分母、去括号、移项、合并、系数化为1(注意不等号的改变问题)
2.
解一元一次不等式的步骤是什么?
情境导入
问题:用每分可抽30t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么?
解:设用x分钟将污水抽完,根据已知条件,我们知道x的取值范围要使不等式
30x
>1200
和
30x<1500同时成立.
合作探究---一元一次不等式组的定义
类似于方程组,我们用大括号把上述两个不等式联立起来,
得:
像
这样,关于同一未知数的两个一元一次不等式合在一起,就组成一个一元一次不等式组.
注意:不等式组中只能含有一个未知数。
小试牛刀
判断下列不等式组是否为一元一次不等式组:
×
×
√
√
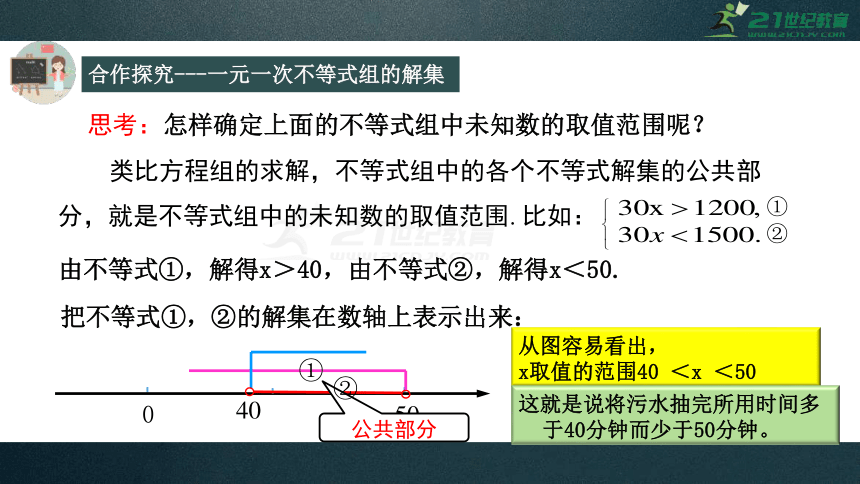
思考:怎样确定上面的不等式组中未知数的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
比如:
合作探究---一元一次不等式组的解集
①
②
由不等式①,解得x>40,由不等式②,解得x<50.
40
0
50
公共部分
②
①
把不等式①,②的解集在数轴上表示出来:
从图容易看出,
x取值的范围40
<x
<50
这就是说将污水抽完所用时间多于40分钟而少于50分钟。
合作探究---一元一次不等式组的解集
归纳:我们把几个一元一次不等式解集的公共部分,叫作由
它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
小试牛刀
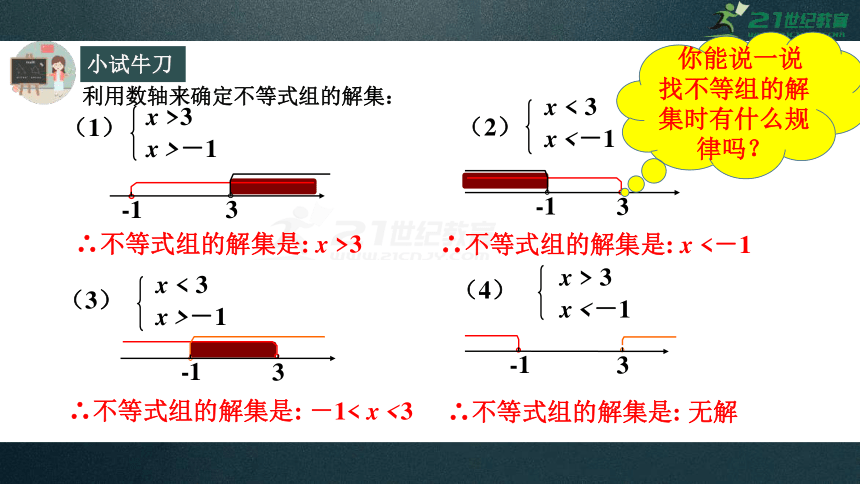
利用数轴来确定不等式组的解集:
x
>3
x
>-1
(1)
∴不等式组的解集是:
x
>3
x
<
3
x
<-1
(2)
∴不等式组的解集是:
x
<-1
x
<
3
x
>-1
(3)
∴不等式组的解集是:
-1<
x
<3
x
>
3
x
<-1
(4)
3
-1
3
-1
3
-1
3
-1
∴不等式组的解集是:
无解
你能说一说找不等组的解集时有什么规律吗?
归纳总结
一般由两个一元一次不等式组成的不等式组由四种基本类型确定,通过下列图示,请说出解集并归纳口诀:(设a一元一次不等式组
解集
图示
口诀
同大取大
同小取小
大小小大中间找
大大小小找不着(无解)
x>b
xa无解
合作探究---一元一次不等式组的求解
解不等式②,得
x
<-3.
例1
(1)
解不等式组:
解:
解不等式①,得
x
≤
3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,所以这个不等式组的解集是
x<-3.
(2)解不等式组:
①
②
解:
解不等式①,得
x
>-2.
解不等式②,得
x
>6.
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
6
由图可知,这个不等式组的解集是x>6.
合作探究---一元一次不等式组的求解
小试牛刀
1、解下列不等式组:
?
0
8
∴不等式组的解集为:无解
2x+3≥
x
+11
,
①
-1<2-x
.
②
2x+5
3
●
小试牛刀
解:解不等式①,得:x≥2
在数轴上表示为:
∴整数x是2
,3.
5x-1≥3(x+1)
x-1<
①
②
x-
解不等式②,得:x<
∴不等式组的解集是
2≤x<
2
0
3
4
3.5
2、求不等式组
的整数解?
课堂小结
这节课你学到了什么?有哪些感受?
实战演练
1、
已知不等式组
的解集为-1<x<1,
则(a+1)(b-1)的值为多少?
2x—a<1
x—2b>3
解:
由不等式组得:
x
<
x
>3+2b
因为不等式组的解集为:
-1<
x
<
1
,
所以:
=1
3+2b=
-1
解得
a=1
,
b=
-
2
所以(a+1)(b-1)=2×(-3)=-6
实战演练
2、要使-11≤3x-2<7成立,x取什么范围?
解:把原式化为不等式组:
3x-2≥-11
3x-2
<7
①
②
解不等式①,得:x≥-3
解不等式②,得:x<3
在数轴上表示为:
-3
3
∴不等式组的解集是
-3
≤
x
<
3
0
即x的取值范围是-3
≤
x
<
3
实战演练
3、若关于x的不等式组
恰有三个整数解,
求实数a的取值范围.
解不等式①:x>-
解不等式②:x<2a.
因为不等式组恰有三个整数解,
所以2<2a≤3.
所以1<a≤
解:
解含字母的不等式,和方程一样,将未知数以外的字母当做已知数进行求解。
实战演练
教材137页3、4、7、8题
https://www.21cnjy.com/help/help_extract.php
人教版
七年级数学下
9.3一元一次不等式组
教学目标
1.通过具体操作,在解一元一次不等式组的过程中形成正确的解不等
式组的思路与方法;(重点、难点)
2.掌握在数轴上正确表示一元一次不等式组的解集的方法.(重点)
回顾旧知
1.怎样解一元一次不等式?
解一元一次不等式,根据不等式的性质,将不等式逐步化
为x>a(或x
去分母、去括号、移项、合并、系数化为1(注意不等号的改变问题)
2.
解一元一次不等式的步骤是什么?
情境导入
问题:用每分可抽30t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么?
解:设用x分钟将污水抽完,根据已知条件,我们知道x的取值范围要使不等式
30x
>1200
和
30x<1500同时成立.
合作探究---一元一次不等式组的定义
类似于方程组,我们用大括号把上述两个不等式联立起来,
得:
像
这样,关于同一未知数的两个一元一次不等式合在一起,就组成一个一元一次不等式组.
注意:不等式组中只能含有一个未知数。
小试牛刀
判断下列不等式组是否为一元一次不等式组:
×
×
√
√
思考:怎样确定上面的不等式组中未知数的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
比如:
合作探究---一元一次不等式组的解集
①
②
由不等式①,解得x>40,由不等式②,解得x<50.
40
0
50
公共部分
②
①
把不等式①,②的解集在数轴上表示出来:
从图容易看出,
x取值的范围40
<x
<50
这就是说将污水抽完所用时间多于40分钟而少于50分钟。
合作探究---一元一次不等式组的解集
归纳:我们把几个一元一次不等式解集的公共部分,叫作由
它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
小试牛刀
利用数轴来确定不等式组的解集:
x
>3
x
>-1
(1)
∴不等式组的解集是:
x
>3
x
<
3
x
<-1
(2)
∴不等式组的解集是:
x
<-1
x
<
3
x
>-1
(3)
∴不等式组的解集是:
-1<
x
<3
x
>
3
x
<-1
(4)
3
-1
3
-1
3
-1
3
-1
∴不等式组的解集是:
无解
你能说一说找不等组的解集时有什么规律吗?
归纳总结
一般由两个一元一次不等式组成的不等式组由四种基本类型确定,通过下列图示,请说出解集并归纳口诀:(设a
解集
图示
口诀
同大取大
同小取小
大小小大中间找
大大小小找不着(无解)
x>b
x
合作探究---一元一次不等式组的求解
解不等式②,得
x
<-3.
例1
(1)
解不等式组:
解:
解不等式①,得
x
≤
3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,所以这个不等式组的解集是
x<-3.
(2)解不等式组:
①
②
解:
解不等式①,得
x
>-2.
解不等式②,得
x
>6.
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
6
由图可知,这个不等式组的解集是x>6.
合作探究---一元一次不等式组的求解
小试牛刀
1、解下列不等式组:
?
0
8
∴不等式组的解集为:无解
2x+3≥
x
+11
,
①
-1<2-x
.
②
2x+5
3
●
小试牛刀
解:解不等式①,得:x≥2
在数轴上表示为:
∴整数x是2
,3.
5x-1≥3(x+1)
x-1<
①
②
x-
解不等式②,得:x<
∴不等式组的解集是
2≤x<
2
0
3
4
3.5
2、求不等式组
的整数解?
课堂小结
这节课你学到了什么?有哪些感受?
实战演练
1、
已知不等式组
的解集为-1<x<1,
则(a+1)(b-1)的值为多少?
2x—a<1
x—2b>3
解:
由不等式组得:
x
<
x
>3+2b
因为不等式组的解集为:
-1<
x
<
1
,
所以:
=1
3+2b=
-1
解得
a=1
,
b=
-
2
所以(a+1)(b-1)=2×(-3)=-6
实战演练
2、要使-11≤3x-2<7成立,x取什么范围?
解:把原式化为不等式组:
3x-2≥-11
3x-2
<7
①
②
解不等式①,得:x≥-3
解不等式②,得:x<3
在数轴上表示为:
-3
3
∴不等式组的解集是
-3
≤
x
<
3
0
即x的取值范围是-3
≤
x
<
3
实战演练
3、若关于x的不等式组
恰有三个整数解,
求实数a的取值范围.
解不等式①:x>-
解不等式②:x<2a.
因为不等式组恰有三个整数解,
所以2<2a≤3.
所以1<a≤
解:
解含字母的不等式,和方程一样,将未知数以外的字母当做已知数进行求解。
实战演练
教材137页3、4、7、8题
https://www.21cnjy.com/help/help_extract.php
