高一数学(人教B版)-10.2.2复数的乘法-PPT课件(共69张PPT)
文档属性
| 名称 | 高一数学(人教B版)-10.2.2复数的乘法-PPT课件(共69张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-14 17:57:12 | ||
图片预览










文档简介
(共69张PPT)
复数的乘法
高一年级
数学
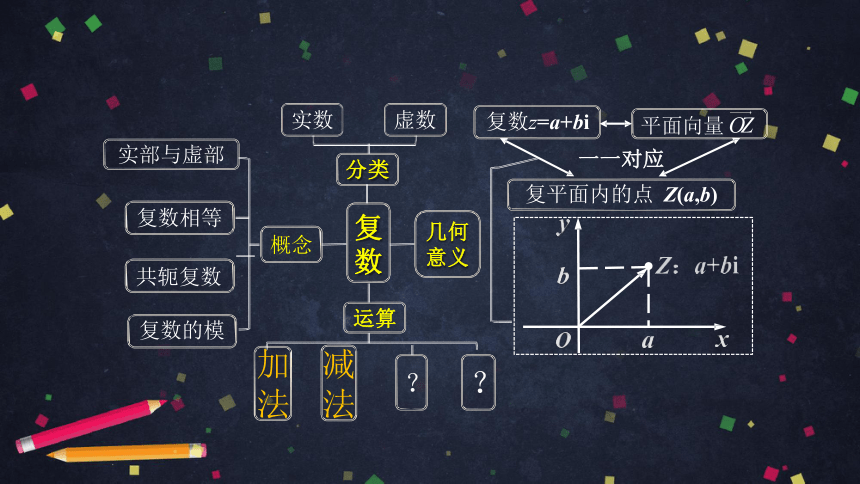
复
数
概念
复数z=a+bi
平面向量OZ
一一对应
复平面内的点
Z(a,b)
几何
意义
分类
实数
虚数
共轭复数
复数相等
复数的模
实部与虚部
?
运算
加
减
法
法
?
?
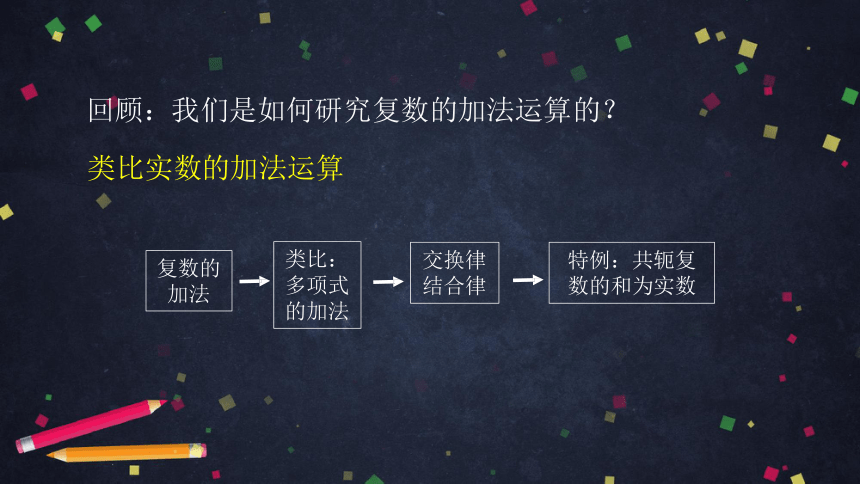
回顾:我们是如何研究复数的加法运算的?
复数的
加法
类比:
多项式
的加法
交换律
结合律
特例:共轭复
数的和为实数
类比实数的加法运算
a,b,c?R时,有
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
ab
?ba,
ab
c
?
a
bc
,
a
b?c
?
ab?ac.
我们知道,实数的乘法运算满足交换律与结合律,
且对加法满足分配律,即:
复数的乘法应该如何规定,才能满足这些运算律
呢?本节课我们将来学习复数的乘法法则.
问题1
1
2
3
设z
?
3,z
?
1?
2i,z
?
2
?
5i
如何计算z
z
与z
z
的值呢?
1
2
2
3
z1
z2
?
3?1?
2i?,
z2
z3
?
?1?
2i??2+5i?.
问题1
类比多项式乘法
a
?m
?
n?
?a
?
b??m
?
n?
1
2
3
设z
?
3,z
?
1?
2i,z
?
2
?
5i
如何计算z
z
与z
z
的值呢?
1
2
2
3
z1
z2
?
3?1?
2i?,
z2
z3
?
?1?
2i??2+5i?.
问题1
请你尝试给出任意两个复数相乘的运算法则.
类比多项式乘法
?a
?
b??m
?
n?
a
?m
?
n?
=am
?
an.
=am
?
an+bm
?
bn.
设z
?
3,z
?
1?
2i,z
?
2
?
5i
1
2
3
如何计算z
z
与z
z
的值呢?
z2
z3
?
?1?
2i??2+5i?.
1
2
2
3
z1
z2
?
3?1?
2i?,
复数的乘法法则:
?
ac
?
adi
?
bci
?
bdi2
类比多项式乘法
一般地,设z1
?
a
?
bi,z2
?
c
?
di?a,
b,
c,
d
?
R
?,称z1
z2
?或z1
?
z2
?
为z1与z2的积,并规定:
z1
z2
?
?a
?
bi??c
?
di?
复数的乘法法则:
?
ac
?
adi
?
bci
?
bd
类比多项式乘法
把i2换成-1
?
ac
?
adi
?
bci
?
bdi2
一般地,设z1
?
a
?
bi,z2
?
c
?
di?a,
b,
c,
d
?
R
?,称z1
z2
?或z1
?
z2
?
为z1与z2的积,并规定:
z1
z2
?
?a
?
bi??c
?
di?
复数的乘法法则:
类比多项式乘法
把i2换成-1
利用加法法则
?
ac
?
adi
?
bci
?
bdi2
?
ac
?
adi
?
bci
?
bd
?
?ac
?
bd
?
?
?ad
?
bc
?i.
一般地,设z1
?
a
?
bi,z2
?
c
?
di?a,
b,
c,
d
?
R
?,称z1
z2
?或z1
?
z2
?
为z1与z2的积,并规定:
z1
z2
?
?a
?
bi??c
?
di?
复数的乘法法则:
一般地,设z1
?
a
?
bi,z2
?
c
?
di?a,
b,
c,
d
?
R
?,称z1
z2
?或z1
?
z2
?
为z1与z2的积,并规定:
z1
z2
?
?a
?
bi??c
?
di?
?
ac
?
adi
?
bci
?
bdi2
?
ac
?
adi
?
bci
?
bd
?
?ac
?
bd
?
?
?ad
?
bc
?i.
符号
语言
运算
思路:
类比多项式乘法.
运算
两个复数的积仍然
结果:是复数.
例如,对于前面的问题,已知:
z
?
3,z
?
1?
2i,z
?
2
?
5i
1
2
3
则有:
z1
z2
?
3?1?
2i?
?
3
?
6i,
z2
z3
?
?1?
2i??2
?
5i?
?
2
?
5i
?
4i
?10i
?
2
?
i
?10
?
12
?
i.
2
z2
z1
,
z1
?
z2
z3
?,?
z1z2
?
z3的值.
1
2
3
已知:z
?
3,z
?
1?
2i,z
?
2
?
5i,请你再算一算
z2
z1
?
?1?
2i??
3
?
3
?
6i,
z2
z1
,
z1
?
z2
z3
?,?
z1z2
?
z3的值.
1
2
3
已知:z
?
3,z
?
1?
2i,z
?
2
?
5i,请你再算一算
解:
z1
?
z2
z3
?
?
3
???1?
2i??2
?
5i???
?
3?12
?
i?
?
36
?
3i
?
z1
z2
?
z3
?
??3?1?
2i???
?2
?
5i?
?
?3
?
6i??2
?
5i?
?
6
?15i
?12i
?
30i2
?
36
?
3i.
z2
z1
?
?1?
2i??
3
?
3
?
6i
?
z1
z2
,
z2
z1
,
z1
?
z2
z3
?,?
z1z2
?
z3的值.
1
2
3
已知:z
?
3,z
?
1?
2i,z
?
2
?
5i,请你再算一算
解:
z1
?
z2
z3
?
?
3
???1?
2i??2
?
5i???
?
3?12
?
i?
?
36
?
3i
?
z1
z2
?
z3
?
??3?1?
2i???
?2
?
5i?
?
?3
?
6i??2
?
5i?
?
6
?15i
?12i
?
30i2
?
36
?
3i.
证明思路:
设z1
?
a
?
bi,z2
?
c
?
di,z3
?
e
?
fi
?a,
b,
c,
d
,
e,
f
?
R
?
分别计算左右结果;
验证实部虚部是否都相等.
复数的乘法法则满足交换律和结合律.
即:
z1
z2
?
z2
z1,
?
z1
z2
?
z3
?
z1
?
z2
z3
?.
问题2
复数的乘法法则是否满足分配律?
z1
?
z2
?
z3
?
?
z1
z2
?
z1
z3
.
证明:设z
?
a
?
bi,z
1
2
?
c
?
di,z3
?
e
?
fi
?a,
b,
c,
d
,
e,
f
?
R
?.
z1
?
z2
?
z3
?
=
?a
?
bi??c
?
di
?
e
?
fi?
=
?a
?
bi?
???c
?
e?+
?d
?
f
?i??
?
a
?c
?
e?
?
a
?d
?
f
?i
?
b
?c
?
e?i
?
b
?d
?
f
?i2
=
?ac
?
ae
?
bd
?
bf
?
?
?ad
?
af
?
bc
?
be?i.
证明:设z
?
a
?
bi,z
1
2
?
c
?
di,z3
?
e
?
fi
?a,b,
c,
d
,
e,
f
?
R
?
z1
z2
?
z1
z3
=
?a
?
bi??c
?
di?+
?a
?
bi??e
?
fi?
?
?ac
?
adi
?
bci
?
bdi2
?
?
?ae
?
afi
?
bei
?
bfi2
?
?
ac
?
ae
?
bd
?
bf
?
adi
?
afi
?
bci
?
bei
=
?ac
?
ae
?
bd
?
bf
?
?
?ad
?
af
?
bc
?
be?i.
证明:设z
?
a
?
bi,z
1
2
?
c
?
di,z3
?
e
?
fi
?a,b,
c,
d
,
e,
f
?
R
?
z1
z2
?
z1
z3
=
?a
?
bi??c
?
di?+
?a
?
bi??e
?
fi?
?
?ac
?
adi
?
bci
?
bdi2
?
?
?ae
?
afi
?
bei
?
bfi2
?
?
ac
?
ae
?
bd
?
bf
?
adi
?
afi
?
bci
?
bei
=
?ac
?
ae
?
bd
?
bf
?
?
?ad
?
af
?
bc
?
be?i.
?
z1
?
z2
?
z3
?.
复数的乘法法则满足交换律、结合律和分配律.
即:
交换律:
z1
z2
?
z2
z1
,
结合律:?
z1
z2
?
z3
?
z1
?
z2
z3
?,
分配律:
z1
?
z2
?
z3
?
?
z1
z2
?
z1
z3
.
1?
z
?
z
?1
?
z.
例如:
?1?
2i??3
?
4i?+
?1?
2i??5
?
4i?.
分析:观察式子,为两个乘积的和的问题,而两个乘法
运算中均含有相同因数?1?
2i?
所以我们可以利用分配律
先计算
?3
?
4i?
与
?5
?
4i?的和,再用
?1?
2i?
与它们的和
相乘.
例如:
?1?
2i??3
?
4i?+
?1?
2i??5
?
4i?.
解:原式
=
?1?
2i?
???3
?
4i?+
?5
?
4i???
=
?1?
2i??8
?
8
?16i
同时,用同样的方法可以验证等式的性质仍然成立.
等式的性质:即当z1
?
z2时,必有z1z
?
z2
z
.
问题3
下列运算能否用更简单的方式表示?
(1)
2i?
2i?
2i?
2i
(2)
?1?
i??1?
i??1?
i??1?
i?
我们知道,在实数范围内,n个相同因数的乘积
的运算,称为乘方运算.乘方的运算结果叫做幂.实数
的正整数次幂满足:
aman
?
am?n
,
?am
?n
?
amn
,
?ab?n
?
anbn
?m,
n
?
N
?.
+
同样,我们可以定义复数的乘方运算:
n个相同的复数z
相乘时,称为z
的n次方(或n
次幂),并记作zn
,即zn
?
z
?
z
?
z
.
n个
同样,我们可以定义复数的乘方运算:
n个相同的复数z
相乘时,称为z
的n次方(或n
次幂),并记作zn
,即zn
?
z
?
z
?
z
.
n个
例如:(1)2i?
2i?
2i?
2i=
?2i?4
(2)?1?
i??1?
i??1?
i??1?
i?=
?1?
i?2
?1?
i?2
?
?
1
2
1
2
n
.
?zm
?n
z
z
可以验证,复数的正整数次幂满足:
当m,
n均为正整数时,
zm
zn
?
zm?n
,
?
zmn
,
n
?
z
n
z
由此可知
i3
?
i2
?i
?
?i,
?
i2
?i2
?
??1????1?
?
1,
i4
i5
?
i4
?
i
?
i.
i6
i7
i8
?
i4
?i2
?
?1,
?
i4
?i3
?
?i,
?
i4
?i4
?
1.
由此可知
i3
?
i2
?i
?
?i,
?
i2
?i2
?
??1????1?
?
1,
i4
i5
?
i4
?
i
?
i.
i
i2
i3
i4
i5
?
i
i6
?
i2
i7
?
i3
i8
?
i4
i
?1
?i
1
i
?1
?i
1
i
i2
i3
i4
i5
?
i
i6
?
i2
i7
?
i3
i8
?
i4
i
?1
?i
1
i
?1
?i
1
in
1,
n
?
4k,
?
?
i,
n
?
4k
?
3,
?
?
??1,
n
?
4k
?
2,
+
k
?
N
.
??
?i,
n
?
4k
?1,
那么2i?
2i?
2i?
2i=
?2i?4
=24
i4
=16.
例
1
计算:(1)?3
?
2i??3
?
2i?
(2)?a
?
bi??a
?
bi?.
分析:此题考查的运算是两个复数的乘
法,可以利用乘法法则求解.
例
1
计算:(1)?3
?
2i??3
?
2i?
(2)?a
?
bi??a
?
bi?.
?
9
?
6i
?
6i
?
4i2
?
13;
?
a2
?
abi
?
abi
?
b2i2
?
a2
?
b2
.
(1)原式
(2)原式
方法一:利用乘法法则.
解:
例
1
计算:(1)?3
?
2i??3
?
2i?
(2)?a
?
bi??a
?
bi?.
分析:观察式子结构,形如
?a
?
b??a
?
b?
可以尝试利用实数乘法运算中的平方差公式求
解.
例
1
计算:(1)?3
?
2i??3
?
2i?
(2)?a
?
bi??a
?
bi?.
?
32
?
?2i?2
?
9
?
4
?
13
?
a2
?
?bi?2
?
a2
?
b2
.
(2)原式
(1)原式
方法二:利用平方差公式.
解:
小结:复数的乘法在计算过程中按照复数的乘法法
则进行,其中实数运算中的平方差公式也适用于复数的
乘法.
?
??
?
2
1
2
1
2
1
2
平方差公式:
z
?
z
z
?
z
?
z
?
z
2
.
观察例
1
的两个题目
?3
?
2i??3
?
2i?
=13
?a
?
bi??a
?
bi?
?
a2
?
b2
.
观察例
1
的两个题目
?3
?
2i??3
?
2i?
=13
?a
?
bi??a
?
bi?
?
a2
?
b2
.
观察例
1
的两个题目
?3
?
2i??3
?
2i?
=13
?a
?
bi??a
?
bi?
?
a2
?
b2
.
观察例
1
的两个题目
?3
?
2i??3
?
2i?
=13
.
?a
?
bi??a
?
bi?
?
a2
?
b2
?a
?
bi??a
?
bi?
?
a
?
bi
2
?
a
?
bi
2
?
a2
?
b2
.
小结:两个共轭复数的乘积等于其模的平方.
即:?z
?
C,
zz
?
z
2
?
z
2
.
分析:此题考查的是复数的乘方运算,可以先利
用乘方运算的定义将问题转化成两个复数的乘积,再
利用复数的乘法法则来求解.
例
2
计算?1
?
5i?2
.
例
2
计算?1
?
5i?2
.
方法一:根据复数乘方的定义和复数乘法法则.
解:
原式?
?1?
5i??1?
5i?
?
1?
5i
?
5i
?
25i2
?
?24
?10i.
可以尝试利用
分析:观察式子结构,形如
?a
?
b?2
实数乘法运算中的完全平方公式求解.
例
2
计算?1
?
5i?2
.
例
2
计算?1
?
5i?2
.
方法二:利用完全平方公式.
解:
原式?
1+2?1?
5i
?
?5i?2
?
?24
?10i.
小结:实数运算中的完全平方公式和平方差公式同
样适用于复数的乘法.在计算过程中应注意观察,适时
的利用公式使运算过程更简捷.
?
?
2
2
1
2
1
1
2
2
完全平方公式:
z
?
z
?
z
?
2z
z
z
2
?
??
?
2
1
2
1
2
1
2
平方差公式:
z
?
z
z
?
z
?
z
?
z
2
.
分析:此题考查的是两个幂相乘的运算,可先利
用完全平方公式,分别计算出?1?
i?2
与?1?i?2
的值,再
计算它们的乘积.
例
3
计算?1?
i?2
?1?
i?2
的值.
例
3
计算?1?
i?2
?1?
i?2
的值.
方法一:先乘方,再乘积.
=
?12
?
2i
?
i2
??12
?
2i
?
i2
?
?
2i???2i?
?
4.
原式
解:
例
3
计算?1?
i?2
?1?
i?2
的值.
?
2i
?
i2
?
=
?12
?
2i
?
i2
??12
?
2i???2i?
?
4.
原式
方法一:先乘方,再乘积.
?1?
i?2
=2i,
?1?
i?2
?
?2i.
解:
?
?
1
2
1
2
n
n
n
z
z
?
z
z
?
??
?
2
,将式子变形为?
1?
i
1?i
?
?
?
,其中,
括号内的式子可用平方差公式计算.
例
3
计算?1?
i?2
?1?
i?2
的值.
分析:可根据正整数次幂的运算法则
例
3
计算?1?
i?2
?1?
i?2
的值.
方法二:先乘积,后乘方.
?
???1?
i??1?
i???2
?
?1?
i2
?2
?
22
?
4.
解:
原式
?
???1?
i??1?
i???2
?
?1?
i2
?2
?
22
?
4.
方法二:先乘积,后乘方.
例
3
计算?1?
i?2
?1?
i?2
的值.
?1?
i??1?
i?=2.
解:
原式
小结:针对运算问题,要选择适当的运算公式、设
计合理的运算程序,综合运用运算方法,形成规范化思
考问题的习惯.
复数的乘法
法则
z
z
?
?a
?
bi??c
?
di?
?
ac
?
adi
?
bci
?
bdi2
.
1
2
运算律
交换律、结合律、分配律.
乘法公式
完全平方公式、平方差公式.
重要结论
两个共轭复数的乘积等于其模的平方,为一个实数.
?其中a,
b,
c,
d
?
R
?
复数的乘方
定义
zn
?
z
?
z
?
z
.
n个
运算
法则
zm
zn
?
zm?n
,?zm
?n
?
zmn
,?
z
z
?n
?
z
n
z
n
.
1
2
1
2
?其中m,n
?
N?
?
复数乘法运算:
明确
运算
对象
确定
运算
法则
选择
运算
方法
设计
运算
程序
求得
运算
结果
复数
运算律
乘法公式
乘法法则
幂的运算
法则
运算
顺序
复数
在运算过程中要注意合理性、准确性、熟练性和
简捷性.养成一丝不苟、严谨求实的科学精神.
复
数
概念
复数z=a+bi
平面向量OZ
一一对应
复平面内的点
Z(a,b)
几何
意义
分类
实数
虚数
共轭复数
复数相等
复数的模
实部与虚部
?
运算
减
法
?
乘
法
加
法
1.计算下列各式的值.
(1)?4
?
8i?i;
(2)?i?11
?
2i?;
(4)?1
?
i??1
?
i?;
(3)?3
?
2i?2
;
(5)?1
?
2i??2
?
i??3
?
4i?;
(6)?a
?
bi??a
?
bi???a
?
bi???a
?
bi?,其中a,b
?
R.
2.计算i28,i37,i42,i90
的值.
复数的乘法
高一年级
数学
复
数
概念
复数z=a+bi
平面向量OZ
一一对应
复平面内的点
Z(a,b)
几何
意义
分类
实数
虚数
共轭复数
复数相等
复数的模
实部与虚部
?
运算
加
减
法
法
?
?
回顾:我们是如何研究复数的加法运算的?
复数的
加法
类比:
多项式
的加法
交换律
结合律
特例:共轭复
数的和为实数
类比实数的加法运算
a,b,c?R时,有
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
ab
?ba,
ab
c
?
a
bc
,
a
b?c
?
ab?ac.
我们知道,实数的乘法运算满足交换律与结合律,
且对加法满足分配律,即:
复数的乘法应该如何规定,才能满足这些运算律
呢?本节课我们将来学习复数的乘法法则.
问题1
1
2
3
设z
?
3,z
?
1?
2i,z
?
2
?
5i
如何计算z
z
与z
z
的值呢?
1
2
2
3
z1
z2
?
3?1?
2i?,
z2
z3
?
?1?
2i??2+5i?.
问题1
类比多项式乘法
a
?m
?
n?
?a
?
b??m
?
n?
1
2
3
设z
?
3,z
?
1?
2i,z
?
2
?
5i
如何计算z
z
与z
z
的值呢?
1
2
2
3
z1
z2
?
3?1?
2i?,
z2
z3
?
?1?
2i??2+5i?.
问题1
请你尝试给出任意两个复数相乘的运算法则.
类比多项式乘法
?a
?
b??m
?
n?
a
?m
?
n?
=am
?
an.
=am
?
an+bm
?
bn.
设z
?
3,z
?
1?
2i,z
?
2
?
5i
1
2
3
如何计算z
z
与z
z
的值呢?
z2
z3
?
?1?
2i??2+5i?.
1
2
2
3
z1
z2
?
3?1?
2i?,
复数的乘法法则:
?
ac
?
adi
?
bci
?
bdi2
类比多项式乘法
一般地,设z1
?
a
?
bi,z2
?
c
?
di?a,
b,
c,
d
?
R
?,称z1
z2
?或z1
?
z2
?
为z1与z2的积,并规定:
z1
z2
?
?a
?
bi??c
?
di?
复数的乘法法则:
?
ac
?
adi
?
bci
?
bd
类比多项式乘法
把i2换成-1
?
ac
?
adi
?
bci
?
bdi2
一般地,设z1
?
a
?
bi,z2
?
c
?
di?a,
b,
c,
d
?
R
?,称z1
z2
?或z1
?
z2
?
为z1与z2的积,并规定:
z1
z2
?
?a
?
bi??c
?
di?
复数的乘法法则:
类比多项式乘法
把i2换成-1
利用加法法则
?
ac
?
adi
?
bci
?
bdi2
?
ac
?
adi
?
bci
?
bd
?
?ac
?
bd
?
?
?ad
?
bc
?i.
一般地,设z1
?
a
?
bi,z2
?
c
?
di?a,
b,
c,
d
?
R
?,称z1
z2
?或z1
?
z2
?
为z1与z2的积,并规定:
z1
z2
?
?a
?
bi??c
?
di?
复数的乘法法则:
一般地,设z1
?
a
?
bi,z2
?
c
?
di?a,
b,
c,
d
?
R
?,称z1
z2
?或z1
?
z2
?
为z1与z2的积,并规定:
z1
z2
?
?a
?
bi??c
?
di?
?
ac
?
adi
?
bci
?
bdi2
?
ac
?
adi
?
bci
?
bd
?
?ac
?
bd
?
?
?ad
?
bc
?i.
符号
语言
运算
思路:
类比多项式乘法.
运算
两个复数的积仍然
结果:是复数.
例如,对于前面的问题,已知:
z
?
3,z
?
1?
2i,z
?
2
?
5i
1
2
3
则有:
z1
z2
?
3?1?
2i?
?
3
?
6i,
z2
z3
?
?1?
2i??2
?
5i?
?
2
?
5i
?
4i
?10i
?
2
?
i
?10
?
12
?
i.
2
z2
z1
,
z1
?
z2
z3
?,?
z1z2
?
z3的值.
1
2
3
已知:z
?
3,z
?
1?
2i,z
?
2
?
5i,请你再算一算
z2
z1
?
?1?
2i??
3
?
3
?
6i,
z2
z1
,
z1
?
z2
z3
?,?
z1z2
?
z3的值.
1
2
3
已知:z
?
3,z
?
1?
2i,z
?
2
?
5i,请你再算一算
解:
z1
?
z2
z3
?
?
3
???1?
2i??2
?
5i???
?
3?12
?
i?
?
36
?
3i
?
z1
z2
?
z3
?
??3?1?
2i???
?2
?
5i?
?
?3
?
6i??2
?
5i?
?
6
?15i
?12i
?
30i2
?
36
?
3i.
z2
z1
?
?1?
2i??
3
?
3
?
6i
?
z1
z2
,
z2
z1
,
z1
?
z2
z3
?,?
z1z2
?
z3的值.
1
2
3
已知:z
?
3,z
?
1?
2i,z
?
2
?
5i,请你再算一算
解:
z1
?
z2
z3
?
?
3
???1?
2i??2
?
5i???
?
3?12
?
i?
?
36
?
3i
?
z1
z2
?
z3
?
??3?1?
2i???
?2
?
5i?
?
?3
?
6i??2
?
5i?
?
6
?15i
?12i
?
30i2
?
36
?
3i.
证明思路:
设z1
?
a
?
bi,z2
?
c
?
di,z3
?
e
?
fi
?a,
b,
c,
d
,
e,
f
?
R
?
分别计算左右结果;
验证实部虚部是否都相等.
复数的乘法法则满足交换律和结合律.
即:
z1
z2
?
z2
z1,
?
z1
z2
?
z3
?
z1
?
z2
z3
?.
问题2
复数的乘法法则是否满足分配律?
z1
?
z2
?
z3
?
?
z1
z2
?
z1
z3
.
证明:设z
?
a
?
bi,z
1
2
?
c
?
di,z3
?
e
?
fi
?a,
b,
c,
d
,
e,
f
?
R
?.
z1
?
z2
?
z3
?
=
?a
?
bi??c
?
di
?
e
?
fi?
=
?a
?
bi?
???c
?
e?+
?d
?
f
?i??
?
a
?c
?
e?
?
a
?d
?
f
?i
?
b
?c
?
e?i
?
b
?d
?
f
?i2
=
?ac
?
ae
?
bd
?
bf
?
?
?ad
?
af
?
bc
?
be?i.
证明:设z
?
a
?
bi,z
1
2
?
c
?
di,z3
?
e
?
fi
?a,b,
c,
d
,
e,
f
?
R
?
z1
z2
?
z1
z3
=
?a
?
bi??c
?
di?+
?a
?
bi??e
?
fi?
?
?ac
?
adi
?
bci
?
bdi2
?
?
?ae
?
afi
?
bei
?
bfi2
?
?
ac
?
ae
?
bd
?
bf
?
adi
?
afi
?
bci
?
bei
=
?ac
?
ae
?
bd
?
bf
?
?
?ad
?
af
?
bc
?
be?i.
证明:设z
?
a
?
bi,z
1
2
?
c
?
di,z3
?
e
?
fi
?a,b,
c,
d
,
e,
f
?
R
?
z1
z2
?
z1
z3
=
?a
?
bi??c
?
di?+
?a
?
bi??e
?
fi?
?
?ac
?
adi
?
bci
?
bdi2
?
?
?ae
?
afi
?
bei
?
bfi2
?
?
ac
?
ae
?
bd
?
bf
?
adi
?
afi
?
bci
?
bei
=
?ac
?
ae
?
bd
?
bf
?
?
?ad
?
af
?
bc
?
be?i.
?
z1
?
z2
?
z3
?.
复数的乘法法则满足交换律、结合律和分配律.
即:
交换律:
z1
z2
?
z2
z1
,
结合律:?
z1
z2
?
z3
?
z1
?
z2
z3
?,
分配律:
z1
?
z2
?
z3
?
?
z1
z2
?
z1
z3
.
1?
z
?
z
?1
?
z.
例如:
?1?
2i??3
?
4i?+
?1?
2i??5
?
4i?.
分析:观察式子,为两个乘积的和的问题,而两个乘法
运算中均含有相同因数?1?
2i?
所以我们可以利用分配律
先计算
?3
?
4i?
与
?5
?
4i?的和,再用
?1?
2i?
与它们的和
相乘.
例如:
?1?
2i??3
?
4i?+
?1?
2i??5
?
4i?.
解:原式
=
?1?
2i?
???3
?
4i?+
?5
?
4i???
=
?1?
2i??8
?
8
?16i
同时,用同样的方法可以验证等式的性质仍然成立.
等式的性质:即当z1
?
z2时,必有z1z
?
z2
z
.
问题3
下列运算能否用更简单的方式表示?
(1)
2i?
2i?
2i?
2i
(2)
?1?
i??1?
i??1?
i??1?
i?
我们知道,在实数范围内,n个相同因数的乘积
的运算,称为乘方运算.乘方的运算结果叫做幂.实数
的正整数次幂满足:
aman
?
am?n
,
?am
?n
?
amn
,
?ab?n
?
anbn
?m,
n
?
N
?.
+
同样,我们可以定义复数的乘方运算:
n个相同的复数z
相乘时,称为z
的n次方(或n
次幂),并记作zn
,即zn
?
z
?
z
?
z
.
n个
同样,我们可以定义复数的乘方运算:
n个相同的复数z
相乘时,称为z
的n次方(或n
次幂),并记作zn
,即zn
?
z
?
z
?
z
.
n个
例如:(1)2i?
2i?
2i?
2i=
?2i?4
(2)?1?
i??1?
i??1?
i??1?
i?=
?1?
i?2
?1?
i?2
?
?
1
2
1
2
n
.
?zm
?n
z
z
可以验证,复数的正整数次幂满足:
当m,
n均为正整数时,
zm
zn
?
zm?n
,
?
zmn
,
n
?
z
n
z
由此可知
i3
?
i2
?i
?
?i,
?
i2
?i2
?
??1????1?
?
1,
i4
i5
?
i4
?
i
?
i.
i6
i7
i8
?
i4
?i2
?
?1,
?
i4
?i3
?
?i,
?
i4
?i4
?
1.
由此可知
i3
?
i2
?i
?
?i,
?
i2
?i2
?
??1????1?
?
1,
i4
i5
?
i4
?
i
?
i.
i
i2
i3
i4
i5
?
i
i6
?
i2
i7
?
i3
i8
?
i4
i
?1
?i
1
i
?1
?i
1
i
i2
i3
i4
i5
?
i
i6
?
i2
i7
?
i3
i8
?
i4
i
?1
?i
1
i
?1
?i
1
in
1,
n
?
4k,
?
?
i,
n
?
4k
?
3,
?
?
??1,
n
?
4k
?
2,
+
k
?
N
.
??
?i,
n
?
4k
?1,
那么2i?
2i?
2i?
2i=
?2i?4
=24
i4
=16.
例
1
计算:(1)?3
?
2i??3
?
2i?
(2)?a
?
bi??a
?
bi?.
分析:此题考查的运算是两个复数的乘
法,可以利用乘法法则求解.
例
1
计算:(1)?3
?
2i??3
?
2i?
(2)?a
?
bi??a
?
bi?.
?
9
?
6i
?
6i
?
4i2
?
13;
?
a2
?
abi
?
abi
?
b2i2
?
a2
?
b2
.
(1)原式
(2)原式
方法一:利用乘法法则.
解:
例
1
计算:(1)?3
?
2i??3
?
2i?
(2)?a
?
bi??a
?
bi?.
分析:观察式子结构,形如
?a
?
b??a
?
b?
可以尝试利用实数乘法运算中的平方差公式求
解.
例
1
计算:(1)?3
?
2i??3
?
2i?
(2)?a
?
bi??a
?
bi?.
?
32
?
?2i?2
?
9
?
4
?
13
?
a2
?
?bi?2
?
a2
?
b2
.
(2)原式
(1)原式
方法二:利用平方差公式.
解:
小结:复数的乘法在计算过程中按照复数的乘法法
则进行,其中实数运算中的平方差公式也适用于复数的
乘法.
?
??
?
2
1
2
1
2
1
2
平方差公式:
z
?
z
z
?
z
?
z
?
z
2
.
观察例
1
的两个题目
?3
?
2i??3
?
2i?
=13
?a
?
bi??a
?
bi?
?
a2
?
b2
.
观察例
1
的两个题目
?3
?
2i??3
?
2i?
=13
?a
?
bi??a
?
bi?
?
a2
?
b2
.
观察例
1
的两个题目
?3
?
2i??3
?
2i?
=13
?a
?
bi??a
?
bi?
?
a2
?
b2
.
观察例
1
的两个题目
?3
?
2i??3
?
2i?
=13
.
?a
?
bi??a
?
bi?
?
a2
?
b2
?a
?
bi??a
?
bi?
?
a
?
bi
2
?
a
?
bi
2
?
a2
?
b2
.
小结:两个共轭复数的乘积等于其模的平方.
即:?z
?
C,
zz
?
z
2
?
z
2
.
分析:此题考查的是复数的乘方运算,可以先利
用乘方运算的定义将问题转化成两个复数的乘积,再
利用复数的乘法法则来求解.
例
2
计算?1
?
5i?2
.
例
2
计算?1
?
5i?2
.
方法一:根据复数乘方的定义和复数乘法法则.
解:
原式?
?1?
5i??1?
5i?
?
1?
5i
?
5i
?
25i2
?
?24
?10i.
可以尝试利用
分析:观察式子结构,形如
?a
?
b?2
实数乘法运算中的完全平方公式求解.
例
2
计算?1
?
5i?2
.
例
2
计算?1
?
5i?2
.
方法二:利用完全平方公式.
解:
原式?
1+2?1?
5i
?
?5i?2
?
?24
?10i.
小结:实数运算中的完全平方公式和平方差公式同
样适用于复数的乘法.在计算过程中应注意观察,适时
的利用公式使运算过程更简捷.
?
?
2
2
1
2
1
1
2
2
完全平方公式:
z
?
z
?
z
?
2z
z
z
2
?
??
?
2
1
2
1
2
1
2
平方差公式:
z
?
z
z
?
z
?
z
?
z
2
.
分析:此题考查的是两个幂相乘的运算,可先利
用完全平方公式,分别计算出?1?
i?2
与?1?i?2
的值,再
计算它们的乘积.
例
3
计算?1?
i?2
?1?
i?2
的值.
例
3
计算?1?
i?2
?1?
i?2
的值.
方法一:先乘方,再乘积.
=
?12
?
2i
?
i2
??12
?
2i
?
i2
?
?
2i???2i?
?
4.
原式
解:
例
3
计算?1?
i?2
?1?
i?2
的值.
?
2i
?
i2
?
=
?12
?
2i
?
i2
??12
?
2i???2i?
?
4.
原式
方法一:先乘方,再乘积.
?1?
i?2
=2i,
?1?
i?2
?
?2i.
解:
?
?
1
2
1
2
n
n
n
z
z
?
z
z
?
??
?
2
,将式子变形为?
1?
i
1?i
?
?
?
,其中,
括号内的式子可用平方差公式计算.
例
3
计算?1?
i?2
?1?
i?2
的值.
分析:可根据正整数次幂的运算法则
例
3
计算?1?
i?2
?1?
i?2
的值.
方法二:先乘积,后乘方.
?
???1?
i??1?
i???2
?
?1?
i2
?2
?
22
?
4.
解:
原式
?
???1?
i??1?
i???2
?
?1?
i2
?2
?
22
?
4.
方法二:先乘积,后乘方.
例
3
计算?1?
i?2
?1?
i?2
的值.
?1?
i??1?
i?=2.
解:
原式
小结:针对运算问题,要选择适当的运算公式、设
计合理的运算程序,综合运用运算方法,形成规范化思
考问题的习惯.
复数的乘法
法则
z
z
?
?a
?
bi??c
?
di?
?
ac
?
adi
?
bci
?
bdi2
.
1
2
运算律
交换律、结合律、分配律.
乘法公式
完全平方公式、平方差公式.
重要结论
两个共轭复数的乘积等于其模的平方,为一个实数.
?其中a,
b,
c,
d
?
R
?
复数的乘方
定义
zn
?
z
?
z
?
z
.
n个
运算
法则
zm
zn
?
zm?n
,?zm
?n
?
zmn
,?
z
z
?n
?
z
n
z
n
.
1
2
1
2
?其中m,n
?
N?
?
复数乘法运算:
明确
运算
对象
确定
运算
法则
选择
运算
方法
设计
运算
程序
求得
运算
结果
复数
运算律
乘法公式
乘法法则
幂的运算
法则
运算
顺序
复数
在运算过程中要注意合理性、准确性、熟练性和
简捷性.养成一丝不苟、严谨求实的科学精神.
复
数
概念
复数z=a+bi
平面向量OZ
一一对应
复平面内的点
Z(a,b)
几何
意义
分类
实数
虚数
共轭复数
复数相等
复数的模
实部与虚部
?
运算
减
法
?
乘
法
加
法
1.计算下列各式的值.
(1)?4
?
8i?i;
(2)?i?11
?
2i?;
(4)?1
?
i??1
?
i?;
(3)?3
?
2i?2
;
(5)?1
?
2i??2
?
i??3
?
4i?;
(6)?a
?
bi??a
?
bi???a
?
bi???a
?
bi?,其中a,b
?
R.
2.计算i28,i37,i42,i90
的值.
