湘教版数学七年级下册:4.3 平行线的性质 (共19张PPT)
文档属性
| 名称 | 湘教版数学七年级下册:4.3 平行线的性质 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 680.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-13 12:15:41 | ||
图片预览




文档简介
(共19张PPT)
第4章
平行线的性质
课程标准湘教版教科书
七年级
下
册
数
学
做一做
∠α
∠β;
∠1
∠2.
图4-20
=
=
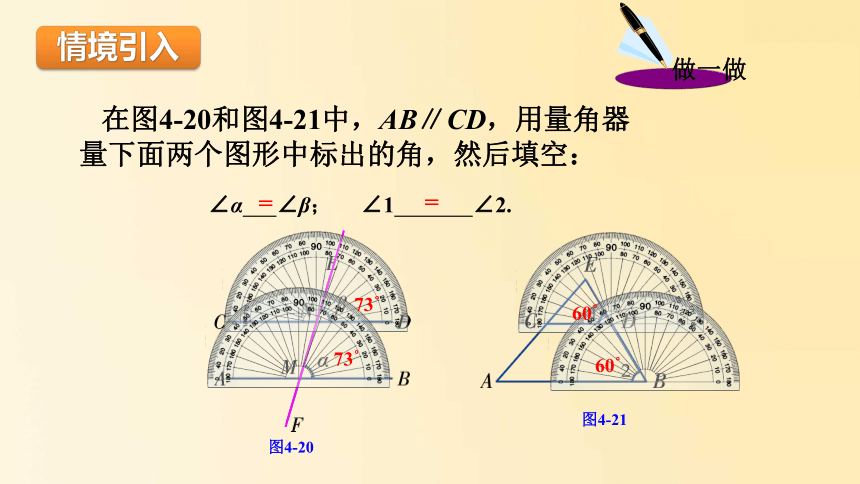
在图4-20和图4-21中,AB∥CD,用量角器量下面两个图形中标出的角,然后填空:
图4-21
情境引入
73°
73°
60°
60°
根据这些操作,你能猜想出什么结论?
我们猜想:如果两条平行直线被第三条直线所截,那么同位角相等.
这个猜想对吗?
情境引入
探究
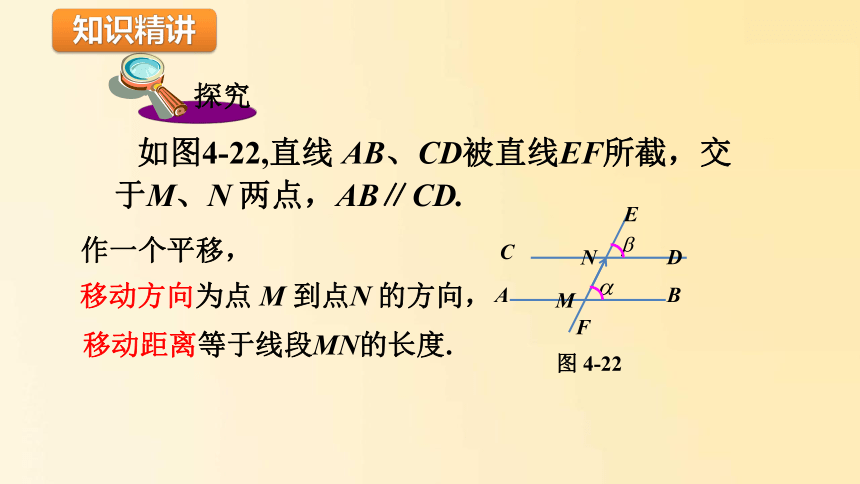
如图4-22,直线
AB、CD被直线EF所截,交于M、N
两点,AB∥CD.
A
B
C
D
E
F
M
N
作一个平移,
图
4-22
知识精讲
移动方向为点
M
到点N
的方向,
移动距离等于线段MN的长度.
探究
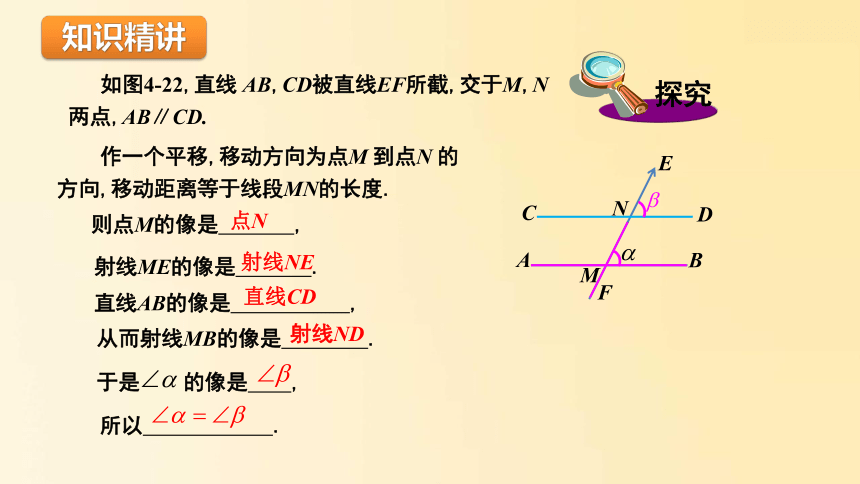
如图4-22,直线
AB,CD被直线EF所截,交于M,N
两点,AB∥CD.
作一个平移,移动方向为点M
到点N
的方向,移动距离等于线段MN的长度.
射线ME的像是
.
点N
射线NE
直线CD
从而射线MB的像是
.
射线ND
直线AB的像是
,
于是
的像是
,
A
B
C
D
E
F
M
N
知识精讲
则点M的像是
,
所以
.
结论
平行线的性质1
知识精讲
两条平行直线被第三条直线所截,同位角相等.
探究
两条平行直线被第三条直线所截,
内错角会具有怎样的数量关系?
如图4-23,平行直线
AB,CD被直线EF所截,
∠1与∠2是内错角.
知识精讲
∠1=∠2
图
4-23
1
2
A
B
C
D
F
E
∵
AB∥CD,
4
∠1=∠4
(两条平行直线被第三条
直线所截,同位角相等).
又
∠2=∠4
(对顶角相等),
(等量代换).
结论
平行线的性质2
知识精讲
两条平行直线被第三条直线所截,内错角相等.
探究
两条平行直线被第三条直线所截,
同旁内角会具有怎样的数量关系?
如图4-23,平行直线
AB,CD被直线EF所截,
∠1与∠3是同旁内角.
∴∠1+∠3=
180o
知识精讲
图
4-23
1
3
A
B
C
D
F
E
4
AB∥CD
,
∴
∠1=∠4
(两条平行直线被第三条
直线所截,同位角相等).
又
∵∠3+∠4
=
180o,
(等量代换).
结论
平行线的性质3
知识精讲
两条平行直线被第三条直线所截,同旁内角互补.
结论
知识精讲
平行线的三个性质可以简单的说成:
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
举
例
例1
如图,直线AB,CD被直线EF所截,
AB∥CD,∠1=100°,试求∠3的度数.
知识精讲
做一做
在例1中,你能分别用平行线的性质2和性质3求出∠3的度数吗?
例1
如图,直线AB,CD被直线EF所截,AB∥CD,∠1=100°,试求∠3的度数.
知识精讲
举
例
例2
如图,AD∥BC,
∠B=
∠D.
试问∠A与∠C相等吗?为什么?
知识精讲
解:
∵
AD∥BC,
∠C+
∠D=180o
(两直线平行,
同旁内角互补.)
又∵
∠B=
∠D
∠A=
∠C
∠A+
∠B=180o
(等角的补角相等.)
小结
(1)平行线的性质是什么?
(2)平行线的三个性质是怎样得到的?
课堂小结
练习
1.
如图,AB∥CD,CD∥EF,BC∥ED,
∠B=70°.求∠C,∠D和∠E的度数.
当堂检测
70o
解:
∵
AB∥CD
∴
∠C=
∠B=70°
(两直线平行,内错角相等.)
∵
BC∥ED
∴
∠C+
∠D=180o
(两直线平行,同旁内角互补.)
∴
∠D=180o
-
70o
=110o
又∵
CD∥EF
∴
∠E=
∠D=110o
(两直线平行,内错角相等.)
2、如图,直线AB,CD被直线AE
所截,AB∥CD,∠1=105°.
求∠2,∠3,∠4的度数.
∴∠2=∠1=
105°
∴∠3=180°-∠
2=75°
∴∠4=∠1=105°
当堂检测
解:
∵
AB∥CD
又∵
∠2+
∠3=180°
(两直线平行,内错角相等)
(两直线平行,同位角相等)
(平角的定义)
中考
试题
3、如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=72°,则∠EGF等于
(
)
A.36°
B.54°
C.72°
D.108°
B
当堂检测
中考
试题
4、如图,AB∥CD,若ABE=120°,∠DCE=35°,则∠BEC=
度.
95
当堂检测
第4章
平行线的性质
课程标准湘教版教科书
七年级
下
册
数
学
做一做
∠α
∠β;
∠1
∠2.
图4-20
=
=
在图4-20和图4-21中,AB∥CD,用量角器量下面两个图形中标出的角,然后填空:
图4-21
情境引入
73°
73°
60°
60°
根据这些操作,你能猜想出什么结论?
我们猜想:如果两条平行直线被第三条直线所截,那么同位角相等.
这个猜想对吗?
情境引入
探究
如图4-22,直线
AB、CD被直线EF所截,交于M、N
两点,AB∥CD.
A
B
C
D
E
F
M
N
作一个平移,
图
4-22
知识精讲
移动方向为点
M
到点N
的方向,
移动距离等于线段MN的长度.
探究
如图4-22,直线
AB,CD被直线EF所截,交于M,N
两点,AB∥CD.
作一个平移,移动方向为点M
到点N
的方向,移动距离等于线段MN的长度.
射线ME的像是
.
点N
射线NE
直线CD
从而射线MB的像是
.
射线ND
直线AB的像是
,
于是
的像是
,
A
B
C
D
E
F
M
N
知识精讲
则点M的像是
,
所以
.
结论
平行线的性质1
知识精讲
两条平行直线被第三条直线所截,同位角相等.
探究
两条平行直线被第三条直线所截,
内错角会具有怎样的数量关系?
如图4-23,平行直线
AB,CD被直线EF所截,
∠1与∠2是内错角.
知识精讲
∠1=∠2
图
4-23
1
2
A
B
C
D
F
E
∵
AB∥CD,
4
∠1=∠4
(两条平行直线被第三条
直线所截,同位角相等).
又
∠2=∠4
(对顶角相等),
(等量代换).
结论
平行线的性质2
知识精讲
两条平行直线被第三条直线所截,内错角相等.
探究
两条平行直线被第三条直线所截,
同旁内角会具有怎样的数量关系?
如图4-23,平行直线
AB,CD被直线EF所截,
∠1与∠3是同旁内角.
∴∠1+∠3=
180o
知识精讲
图
4-23
1
3
A
B
C
D
F
E
4
AB∥CD
,
∴
∠1=∠4
(两条平行直线被第三条
直线所截,同位角相等).
又
∵∠3+∠4
=
180o,
(等量代换).
结论
平行线的性质3
知识精讲
两条平行直线被第三条直线所截,同旁内角互补.
结论
知识精讲
平行线的三个性质可以简单的说成:
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
举
例
例1
如图,直线AB,CD被直线EF所截,
AB∥CD,∠1=100°,试求∠3的度数.
知识精讲
做一做
在例1中,你能分别用平行线的性质2和性质3求出∠3的度数吗?
例1
如图,直线AB,CD被直线EF所截,AB∥CD,∠1=100°,试求∠3的度数.
知识精讲
举
例
例2
如图,AD∥BC,
∠B=
∠D.
试问∠A与∠C相等吗?为什么?
知识精讲
解:
∵
AD∥BC,
∠C+
∠D=180o
(两直线平行,
同旁内角互补.)
又∵
∠B=
∠D
∠A=
∠C
∠A+
∠B=180o
(等角的补角相等.)
小结
(1)平行线的性质是什么?
(2)平行线的三个性质是怎样得到的?
课堂小结
练习
1.
如图,AB∥CD,CD∥EF,BC∥ED,
∠B=70°.求∠C,∠D和∠E的度数.
当堂检测
70o
解:
∵
AB∥CD
∴
∠C=
∠B=70°
(两直线平行,内错角相等.)
∵
BC∥ED
∴
∠C+
∠D=180o
(两直线平行,同旁内角互补.)
∴
∠D=180o
-
70o
=110o
又∵
CD∥EF
∴
∠E=
∠D=110o
(两直线平行,内错角相等.)
2、如图,直线AB,CD被直线AE
所截,AB∥CD,∠1=105°.
求∠2,∠3,∠4的度数.
∴∠2=∠1=
105°
∴∠3=180°-∠
2=75°
∴∠4=∠1=105°
当堂检测
解:
∵
AB∥CD
又∵
∠2+
∠3=180°
(两直线平行,内错角相等)
(两直线平行,同位角相等)
(平角的定义)
中考
试题
3、如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=72°,则∠EGF等于
(
)
A.36°
B.54°
C.72°
D.108°
B
当堂检测
中考
试题
4、如图,AB∥CD,若ABE=120°,∠DCE=35°,则∠BEC=
度.
95
当堂检测
