高一数学(人教B版)-复数的运算习题课-PPT课件(44张)
文档属性
| 名称 | 高一数学(人教B版)-复数的运算习题课-PPT课件(44张) |  | |
| 格式 | zip | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-13 20:40:07 | ||
图片预览








文档简介
(共44张PPT)
高一年级
数学
复数运算的习题课
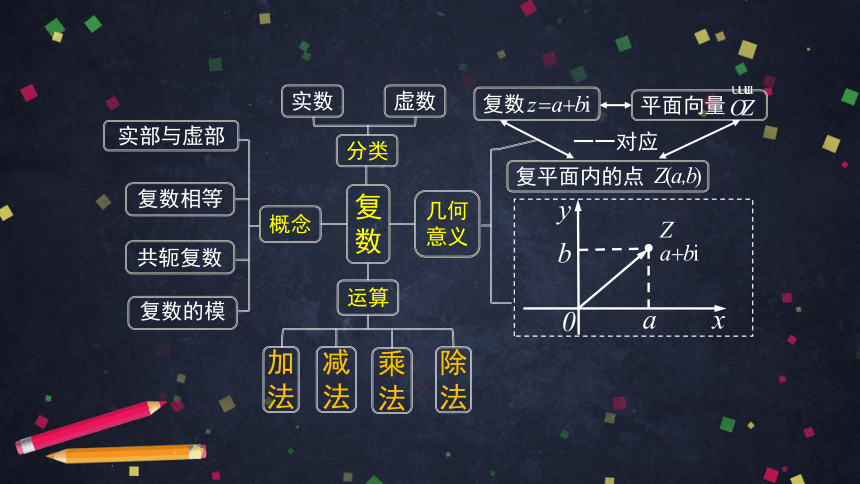
复数
概念
平面向量
一一对应
几何意义
分类
实数
虚数
共轭复数
复数相等
复数的模
实部与虚部
运算
复数
复平面内的点
减法
加法
乘法
除法
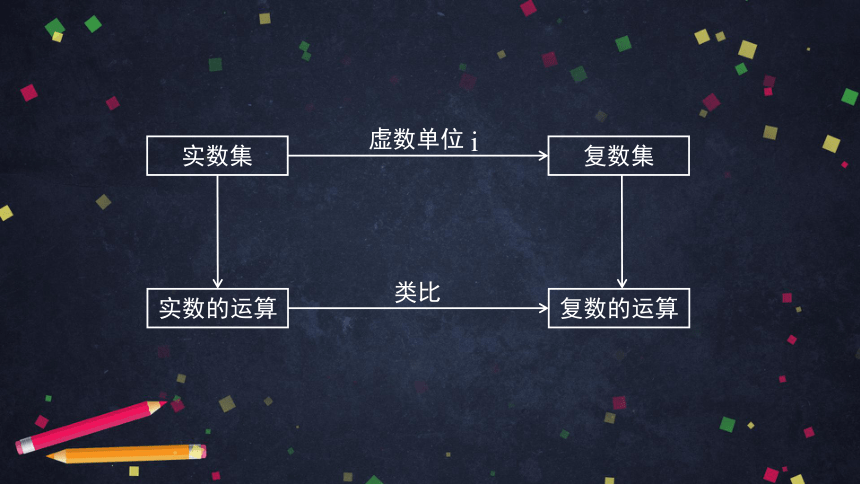
实数集
复数集
虚数单位
实数的运算
复数的运算
类比
知识梳理
运算
实数
复数
加法
交换律:
结合律:
法则:
交换律:
结合律:
减法
定义:
(注:
,
)
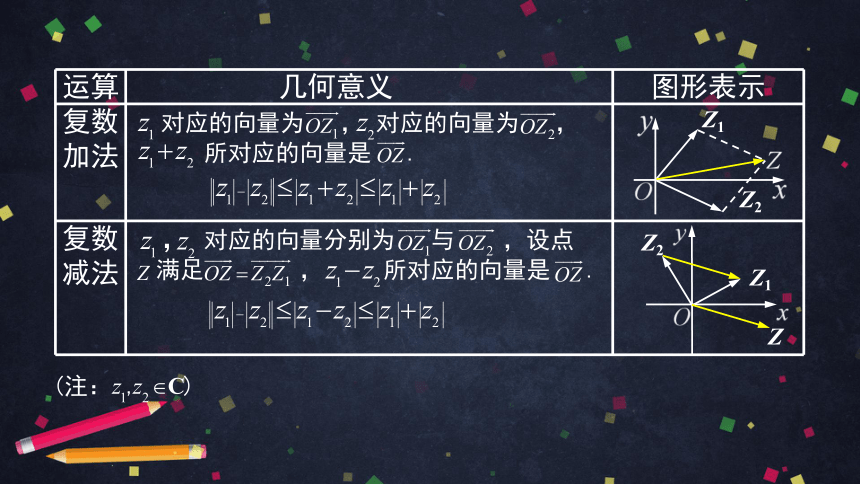
运算
几何意义
图形表示
复数加法
对应的向量为
,
对应的向量为
,
所对应的向量是
.
复数
减法
,
对应的向量分别为
与
,设点
满足
,
所对应的向量是
.
(注:
)
O
Z1
Z
Z2
x
y
O
x
y
Z1
Z2
Z
运算
实数
复数
乘法
多项式乘法:
交换律:
结合律:
分配律:
乘法法则:
交换律:
结合律:
分配律:
除法
定义:
定义:
(注:
,
)
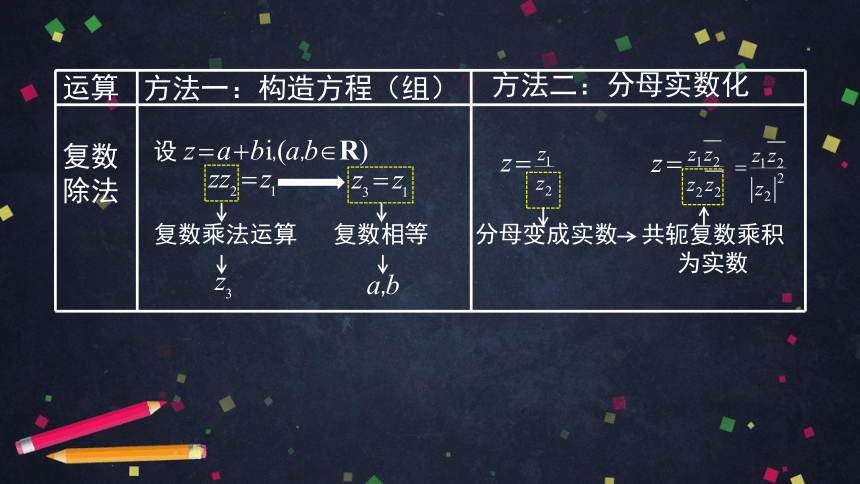
运算
复数
除法
复数乘法运算
复数相等
分母变成实数
共轭复数乘积为实数
方法一:构造方程(组)
方法二:分母实数化
设
运算
实数
复数
乘方
定义:
运算法则:
定义:
运算法则:
(注:
,
,
)
常见结论
典型例题
解:
乘方
算括号内的
乘方运算
减法运算
和的完全平方公式
解:
商
商
分母实数化
除法运算
减法运算
分母实数化
解:
分式
分式
通分
减法运算
除法运算
分母不同
明晰运算对象
厘清运算种类
复数运算
选择运算方法
设计运算程序
求得运算结果
复数
乘除
加减
乘方
运算律
运算法则
公式
运算步骤
方法2:
方法1:
正确解答:
复数的运算法则和运算性质很多与实数范围内的相类似,实数范围内运算的易错点在复数运算时仍易出错.在实数范围内成立的运算性质扩充到复数范围内时,只有经过证明才能使用.
分析与解答:
复数的乘法运算
复数相等的定义
方程组
分母实数化
分析与解答:
分析与解答:
(思维方向:代数)
分析与解答:
圆心在原点
半径为1的圆
(思维方向:几何)
分析与解答:
圆心在原点
半径为1的圆
(思维方向:几何)
分析与解答:
圆心在原点
半径为1的圆
(思维方向:几何)
分析与解答:
向量
向量
(思维方向:向量)
一一对应
复数的代数形式
几何图形
数形结合
平面向量
问题转化
两个虚根互为共轭复数
复数的运算
加法和减法
乘法
类比多项式加减法计算
几何意义:对应向量相加与相减
基本知识
类比多项式乘法计算
除法
分母实数化
运用
复数的四则运算
实系数一元二次方程虚根问题
复数模的问题
类比
思想方法
数形结合
方程思想
核心概念
几何意义
几何意义
模的性质
复数函数
回顾与展望
课后作业
高一年级
数学
复数运算的习题课
复数
概念
平面向量
一一对应
几何意义
分类
实数
虚数
共轭复数
复数相等
复数的模
实部与虚部
运算
复数
复平面内的点
减法
加法
乘法
除法
实数集
复数集
虚数单位
实数的运算
复数的运算
类比
知识梳理
运算
实数
复数
加法
交换律:
结合律:
法则:
交换律:
结合律:
减法
定义:
(注:
,
)
运算
几何意义
图形表示
复数加法
对应的向量为
,
对应的向量为
,
所对应的向量是
.
复数
减法
,
对应的向量分别为
与
,设点
满足
,
所对应的向量是
.
(注:
)
O
Z1
Z
Z2
x
y
O
x
y
Z1
Z2
Z
运算
实数
复数
乘法
多项式乘法:
交换律:
结合律:
分配律:
乘法法则:
交换律:
结合律:
分配律:
除法
定义:
定义:
(注:
,
)
运算
复数
除法
复数乘法运算
复数相等
分母变成实数
共轭复数乘积为实数
方法一:构造方程(组)
方法二:分母实数化
设
运算
实数
复数
乘方
定义:
运算法则:
定义:
运算法则:
(注:
,
,
)
常见结论
典型例题
解:
乘方
算括号内的
乘方运算
减法运算
和的完全平方公式
解:
商
商
分母实数化
除法运算
减法运算
分母实数化
解:
分式
分式
通分
减法运算
除法运算
分母不同
明晰运算对象
厘清运算种类
复数运算
选择运算方法
设计运算程序
求得运算结果
复数
乘除
加减
乘方
运算律
运算法则
公式
运算步骤
方法2:
方法1:
正确解答:
复数的运算法则和运算性质很多与实数范围内的相类似,实数范围内运算的易错点在复数运算时仍易出错.在实数范围内成立的运算性质扩充到复数范围内时,只有经过证明才能使用.
分析与解答:
复数的乘法运算
复数相等的定义
方程组
分母实数化
分析与解答:
分析与解答:
(思维方向:代数)
分析与解答:
圆心在原点
半径为1的圆
(思维方向:几何)
分析与解答:
圆心在原点
半径为1的圆
(思维方向:几何)
分析与解答:
圆心在原点
半径为1的圆
(思维方向:几何)
分析与解答:
向量
向量
(思维方向:向量)
一一对应
复数的代数形式
几何图形
数形结合
平面向量
问题转化
两个虚根互为共轭复数
复数的运算
加法和减法
乘法
类比多项式加减法计算
几何意义:对应向量相加与相减
基本知识
类比多项式乘法计算
除法
分母实数化
运用
复数的四则运算
实系数一元二次方程虚根问题
复数模的问题
类比
思想方法
数形结合
方程思想
核心概念
几何意义
几何意义
模的性质
复数函数
回顾与展望
课后作业
