六年级下册数学课件圆柱圆锥人教版 (共27张)
文档属性
| 名称 | 六年级下册数学课件圆柱圆锥人教版 (共27张) |  | |
| 格式 | zip | ||
| 文件大小 | 697.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-12 20:27:29 | ||
图片预览





文档简介
(共27张PPT)
圆柱圆锥复习专题
复习:
1、圆柱与圆锥各有哪些特征?
2、
怎样求圆柱的侧面积,表面积,体积?计算公式各是什么?
3、
怎样求圆锥的体积?计算公式是什么?
4、圆柱和圆锥常见题型及解题技巧。
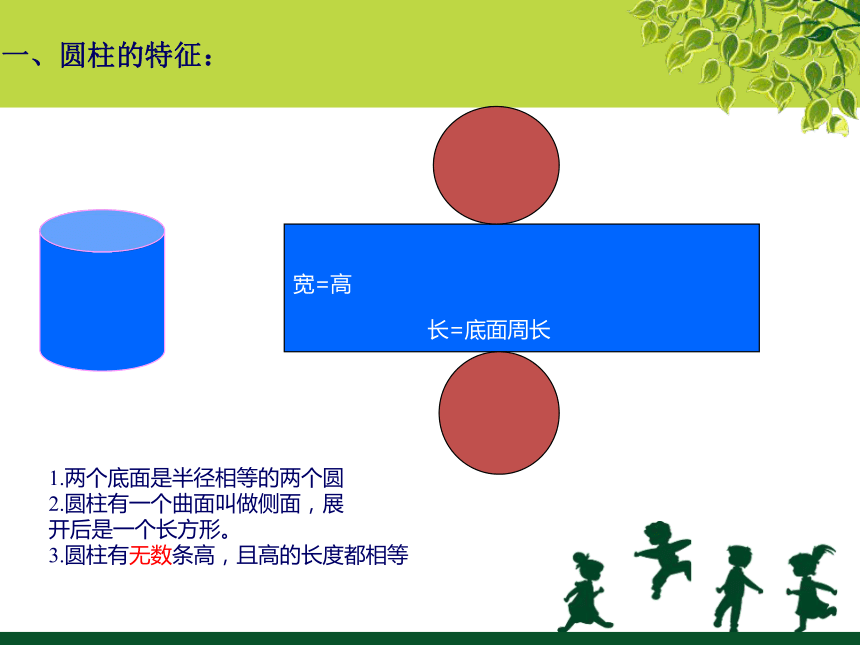
一、圆柱的特征:
宽=高
长=底面周长
1.两个底面是半径相等的两个圆
2.圆柱有一个曲面叫做侧面,展
开后是一个长方形。
3.圆柱有无数条高,且高的长度都相等
h
扇形
圆形
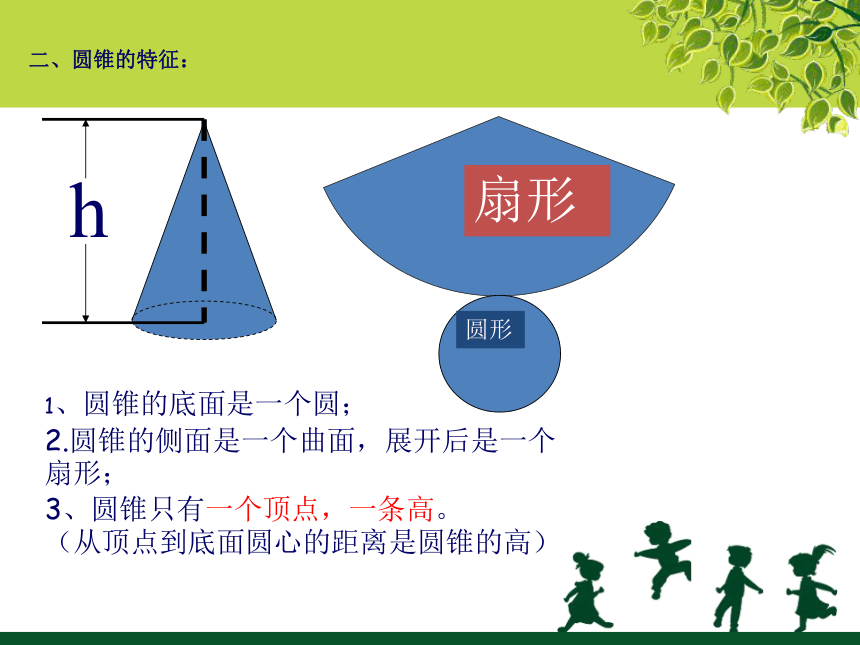
二、圆锥的特征:
1、圆锥的底面是一个圆;
2.圆锥的侧面是一个曲面,展开后是一个扇形;
3、圆锥只有一个顶点,一条高。
(从顶点到底面圆心的距离是圆锥的高)
三、圆锥和圆锥的计算相关公式:
四、圆柱圆锥的常考相关题型:
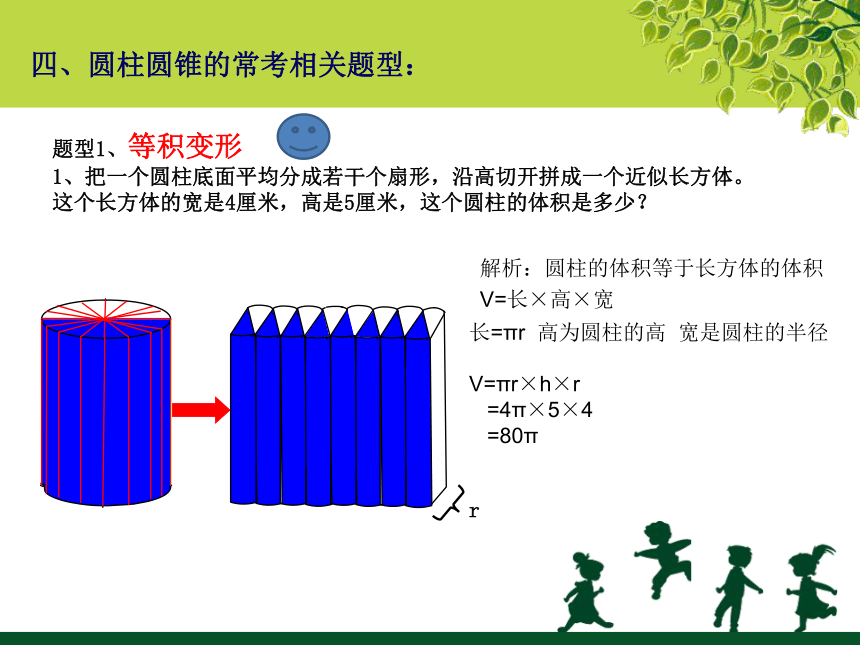
题型1、等积变形
1、把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体。
这个长方体的宽是4厘米,高是5厘米,这个圆柱的体积是多少?
r
解析:圆柱的体积等于长方体的体积
V=长×高×宽
四、圆柱圆锥的常考相关题型:
题型1、等积变形
1、把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体。
这个长方体的宽是4厘米,高是5厘米,这个圆柱的体积是多少?
r
解析:圆柱的体积等于长方体的体积
V=长×高×宽
长=πr
高为圆柱的高
宽是圆柱的半径
V=πr×h×r
=4π×5×4
=80π
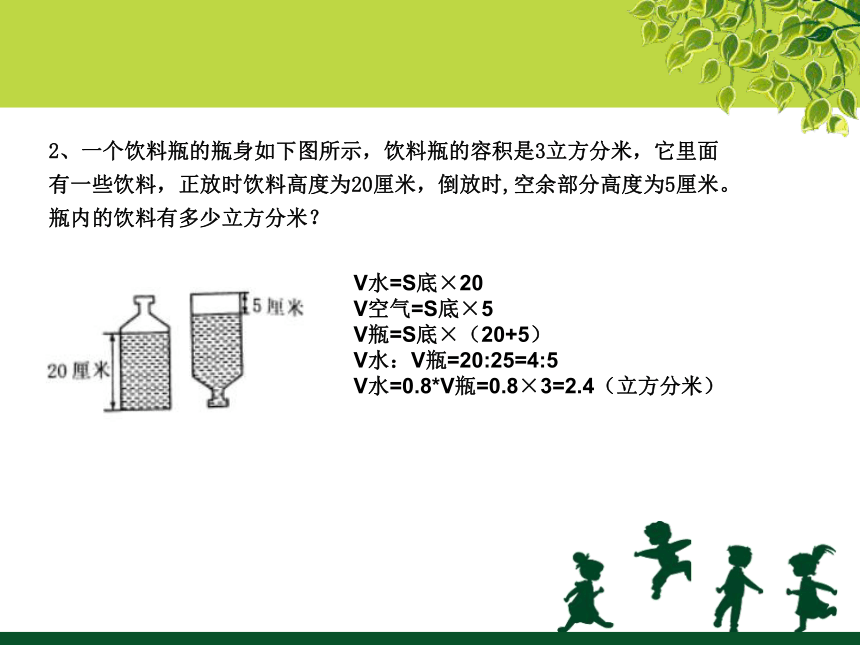
2、一个饮料瓶的瓶身如下图所示,饮料瓶的容积是3立方分米,它里面有一些饮料,正放时饮料高度为20厘米,倒放时,空余部分高度为5厘米。瓶内的饮料有多少立方分米?
解析:
V瓶=V水+V空气
都拿规则的圆柱体来计算,当物体形状改变时,体积不变
2、一个饮料瓶的瓶身如下图所示,饮料瓶的容积是3立方分米,它里面有一些饮料,正放时饮料高度为20厘米,倒放时,空余部分高度为5厘米。瓶内的饮料有多少立方分米?
V水=S底×20
V空气=S底×5
V瓶=S底×(20+5)
V水:V瓶=20:25=4:5
V水=0.8
V瓶=0.8×3=2.4(立方分米)
1、一根长4米,底面直径4厘米的圆柱形钢材,把它锯成同样长的3段,表面积比原来增加了多少平方厘米?
二、切割问题
解析:切一刀增加2个面,切成3段,切2刀,增加4个面,增加了就是4个圆形的面积
1、一根长4米,底面直径4厘米的圆柱形钢材,把它锯成同样长的3段,表面积比原来增加了多少平方厘米?
二、切割问题
解析:切一刀增加2个面,切成3段,切2刀,增加4个面,增加了就是4个圆形的面积
r=d÷2=4÷2=2(厘米)
S=πr?×4=3.14×2×2×4=50.24(平方厘米)
2、把一个高为5厘米的圆柱从直径处沿高剖成两个半圆柱,这两个半圆柱的表面积比原来增加80平方厘米,求原来圆柱的表面积是多少?
解析:增加80平方厘米是两个长方形的面积,长方形的长是圆柱底面的直径,长方形的宽是圆柱的高
2、把一个高为5厘米的圆柱从直径处沿高剖成两个半圆柱,这两个半圆柱的表面积比原来增加80平方厘米,求原来圆柱的表面积是多少?
80÷2=40(平方厘米)
d=40÷5=8(厘米)
r=8÷2=4(厘米)
S=上下两个圆面积+周围的长方形面积
S=2
π
R
R+2R
5=32π+40=140.48
(平方厘米)
3、把一个圆锥沿底面直径和高切成形状、大小完全一样的两部分,结果表面积之和比原来增加48平方分米,圆锥的高为6分米,原来圆锥的体积是多少?
解题思路:要求圆锥的体积,需先求得圆锥的底面直径或半径.根据题意,48÷2=24(平方厘米),增加了两个切面,一个面的面积是24平方厘米
因为切面是三角形,圆锥的底面直径和高就是三角形的底和高,根据三角形面积公式,三角形的底即圆锥的底面直径是24×2÷6=8(厘米)
3、把一个圆锥沿底面直径和高切成形状、大小完全一样的两部分,结果表面积之和比原来增加48平方分米,圆锥的高为6分米,原来圆锥的体积是多少?
一个切面的面积:
48÷2=24(平方厘米);
圆锥的底面直径:
24×2÷6,
=48÷6,
=8(厘米);
圆锥的体积:
[1/3]×3.14×(8÷2)?×6,
3.14×16×2,
=100.48(立方厘米);
答:原来圆锥的体积是100.48立方厘米.
五、图形题
2
6
4
1、如图,
你能否求它的体积?(
单位:厘米)
五、图形题
2
6
4
1、如图,
你能否求它的体积?(
单位:厘米)
五、图形题
2
6
4
1、如图,
你能否求它的体积?(
单位:厘米)
3.14×(2÷2)2×(4+6)÷2=15.7(cm3)
2、如下图所示,有一块长方形铁皮,把其中的阴影部分剪下,正好制成一个圆柱形油桶。求这块长方形铁皮的面积是多少?
16.56cm
2、如下图所示,有一块长方形铁皮,把其中的阴影部分剪下,正好制成一个圆柱形油桶。求这块长方形铁皮的面积是多少?
12.56cm
16.56cm
底面周长+直径
=
16.56分米
所以:
3.14
×
直径+直径=16.56(3.14+1)×直径=16.56
直径=16.56÷4.14=4分米
高=2个直径=2×4=8分米
半径=4÷2=2(分米)
16.56×8=132.48(cm2)
3、一个圆柱高为15厘米,把它的高增加2厘米后表面积增加25.12平方厘米,求原来圆柱的体积。
3、一个圆柱高为15厘米,把它的高增加2厘米后表面积增加25.12平方厘米,求原来圆柱的体积。
底面半径:25.12÷2÷3.14÷2=2(厘米)
体积:3.14×2×2×15=188.4(立方厘米)
六、排水问题
1、一个底面直径是24厘米的圆柱形玻璃杯中装有水,水里放着一个底面直径为12厘米,高18厘米的圆锥形铅块,当铅块从杯中取出时,杯里的水面会下降多少厘米?(注意是完全浸没)
V物=
V排
一个底面直径是24厘米的圆柱形玻璃杯中装有水,水里放着一个底面直径为12厘米,高18厘米的圆锥形铅块,当铅块从杯中取出时,杯里的水面会下降多少厘米?(注意是完全浸没)
V水面下降的体积(圆柱)=V圆锥
r圆锥=12÷2=6(㎝)
V圆锥=1/3×3.14×6?×18=678.24(㎝?)
r圆柱=24÷2=12(㎝)
S底=3.14×12?=452.16(㎝?)
h=V柱÷S底=678.24÷452.16=1.5(㎝)
总结:
1、圆柱、圆柱问题公式简单,计算量较大,一定要注意是求表面积还是体积。一定要把公式写上,公式写对也给分。
2、圆柱的表面积一定要注意圆柱是的底面有几个,一般有三种情况。没有圆面(烟囱),一个圆面(无盖水桶),两个圆面。(正常)
3、圆锥的体积公式不要忘了乘三分之一。
作业
1、一个圆柱的底面半径是3厘米,若它的高增加后表面积将增加37.68平方厘米,求增加部分的体积。
2、把一个高5分米的圆柱的底面分成许多相等的扇形,然后把圆柱切开,再拼成一个近似的长方体,表面积增加了40平方分米。圆柱的体积是多少立方分米?
3、一个圆锥形的小麦堆,底面积是62.8平方米,高是1.2米。如果将这堆小麦在10米宽的公路上铺2厘米厚,能铺多少米?
Bye-bye!
圆柱圆锥复习专题
复习:
1、圆柱与圆锥各有哪些特征?
2、
怎样求圆柱的侧面积,表面积,体积?计算公式各是什么?
3、
怎样求圆锥的体积?计算公式是什么?
4、圆柱和圆锥常见题型及解题技巧。
一、圆柱的特征:
宽=高
长=底面周长
1.两个底面是半径相等的两个圆
2.圆柱有一个曲面叫做侧面,展
开后是一个长方形。
3.圆柱有无数条高,且高的长度都相等
h
扇形
圆形
二、圆锥的特征:
1、圆锥的底面是一个圆;
2.圆锥的侧面是一个曲面,展开后是一个扇形;
3、圆锥只有一个顶点,一条高。
(从顶点到底面圆心的距离是圆锥的高)
三、圆锥和圆锥的计算相关公式:
四、圆柱圆锥的常考相关题型:
题型1、等积变形
1、把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体。
这个长方体的宽是4厘米,高是5厘米,这个圆柱的体积是多少?
r
解析:圆柱的体积等于长方体的体积
V=长×高×宽
四、圆柱圆锥的常考相关题型:
题型1、等积变形
1、把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体。
这个长方体的宽是4厘米,高是5厘米,这个圆柱的体积是多少?
r
解析:圆柱的体积等于长方体的体积
V=长×高×宽
长=πr
高为圆柱的高
宽是圆柱的半径
V=πr×h×r
=4π×5×4
=80π
2、一个饮料瓶的瓶身如下图所示,饮料瓶的容积是3立方分米,它里面有一些饮料,正放时饮料高度为20厘米,倒放时,空余部分高度为5厘米。瓶内的饮料有多少立方分米?
解析:
V瓶=V水+V空气
都拿规则的圆柱体来计算,当物体形状改变时,体积不变
2、一个饮料瓶的瓶身如下图所示,饮料瓶的容积是3立方分米,它里面有一些饮料,正放时饮料高度为20厘米,倒放时,空余部分高度为5厘米。瓶内的饮料有多少立方分米?
V水=S底×20
V空气=S底×5
V瓶=S底×(20+5)
V水:V瓶=20:25=4:5
V水=0.8
V瓶=0.8×3=2.4(立方分米)
1、一根长4米,底面直径4厘米的圆柱形钢材,把它锯成同样长的3段,表面积比原来增加了多少平方厘米?
二、切割问题
解析:切一刀增加2个面,切成3段,切2刀,增加4个面,增加了就是4个圆形的面积
1、一根长4米,底面直径4厘米的圆柱形钢材,把它锯成同样长的3段,表面积比原来增加了多少平方厘米?
二、切割问题
解析:切一刀增加2个面,切成3段,切2刀,增加4个面,增加了就是4个圆形的面积
r=d÷2=4÷2=2(厘米)
S=πr?×4=3.14×2×2×4=50.24(平方厘米)
2、把一个高为5厘米的圆柱从直径处沿高剖成两个半圆柱,这两个半圆柱的表面积比原来增加80平方厘米,求原来圆柱的表面积是多少?
解析:增加80平方厘米是两个长方形的面积,长方形的长是圆柱底面的直径,长方形的宽是圆柱的高
2、把一个高为5厘米的圆柱从直径处沿高剖成两个半圆柱,这两个半圆柱的表面积比原来增加80平方厘米,求原来圆柱的表面积是多少?
80÷2=40(平方厘米)
d=40÷5=8(厘米)
r=8÷2=4(厘米)
S=上下两个圆面积+周围的长方形面积
S=2
π
R
R+2R
5=32π+40=140.48
(平方厘米)
3、把一个圆锥沿底面直径和高切成形状、大小完全一样的两部分,结果表面积之和比原来增加48平方分米,圆锥的高为6分米,原来圆锥的体积是多少?
解题思路:要求圆锥的体积,需先求得圆锥的底面直径或半径.根据题意,48÷2=24(平方厘米),增加了两个切面,一个面的面积是24平方厘米
因为切面是三角形,圆锥的底面直径和高就是三角形的底和高,根据三角形面积公式,三角形的底即圆锥的底面直径是24×2÷6=8(厘米)
3、把一个圆锥沿底面直径和高切成形状、大小完全一样的两部分,结果表面积之和比原来增加48平方分米,圆锥的高为6分米,原来圆锥的体积是多少?
一个切面的面积:
48÷2=24(平方厘米);
圆锥的底面直径:
24×2÷6,
=48÷6,
=8(厘米);
圆锥的体积:
[1/3]×3.14×(8÷2)?×6,
3.14×16×2,
=100.48(立方厘米);
答:原来圆锥的体积是100.48立方厘米.
五、图形题
2
6
4
1、如图,
你能否求它的体积?(
单位:厘米)
五、图形题
2
6
4
1、如图,
你能否求它的体积?(
单位:厘米)
五、图形题
2
6
4
1、如图,
你能否求它的体积?(
单位:厘米)
3.14×(2÷2)2×(4+6)÷2=15.7(cm3)
2、如下图所示,有一块长方形铁皮,把其中的阴影部分剪下,正好制成一个圆柱形油桶。求这块长方形铁皮的面积是多少?
16.56cm
2、如下图所示,有一块长方形铁皮,把其中的阴影部分剪下,正好制成一个圆柱形油桶。求这块长方形铁皮的面积是多少?
12.56cm
16.56cm
底面周长+直径
=
16.56分米
所以:
3.14
×
直径+直径=16.56(3.14+1)×直径=16.56
直径=16.56÷4.14=4分米
高=2个直径=2×4=8分米
半径=4÷2=2(分米)
16.56×8=132.48(cm2)
3、一个圆柱高为15厘米,把它的高增加2厘米后表面积增加25.12平方厘米,求原来圆柱的体积。
3、一个圆柱高为15厘米,把它的高增加2厘米后表面积增加25.12平方厘米,求原来圆柱的体积。
底面半径:25.12÷2÷3.14÷2=2(厘米)
体积:3.14×2×2×15=188.4(立方厘米)
六、排水问题
1、一个底面直径是24厘米的圆柱形玻璃杯中装有水,水里放着一个底面直径为12厘米,高18厘米的圆锥形铅块,当铅块从杯中取出时,杯里的水面会下降多少厘米?(注意是完全浸没)
V物=
V排
一个底面直径是24厘米的圆柱形玻璃杯中装有水,水里放着一个底面直径为12厘米,高18厘米的圆锥形铅块,当铅块从杯中取出时,杯里的水面会下降多少厘米?(注意是完全浸没)
V水面下降的体积(圆柱)=V圆锥
r圆锥=12÷2=6(㎝)
V圆锥=1/3×3.14×6?×18=678.24(㎝?)
r圆柱=24÷2=12(㎝)
S底=3.14×12?=452.16(㎝?)
h=V柱÷S底=678.24÷452.16=1.5(㎝)
总结:
1、圆柱、圆柱问题公式简单,计算量较大,一定要注意是求表面积还是体积。一定要把公式写上,公式写对也给分。
2、圆柱的表面积一定要注意圆柱是的底面有几个,一般有三种情况。没有圆面(烟囱),一个圆面(无盖水桶),两个圆面。(正常)
3、圆锥的体积公式不要忘了乘三分之一。
作业
1、一个圆柱的底面半径是3厘米,若它的高增加后表面积将增加37.68平方厘米,求增加部分的体积。
2、把一个高5分米的圆柱的底面分成许多相等的扇形,然后把圆柱切开,再拼成一个近似的长方体,表面积增加了40平方分米。圆柱的体积是多少立方分米?
3、一个圆锥形的小麦堆,底面积是62.8平方米,高是1.2米。如果将这堆小麦在10米宽的公路上铺2厘米厚,能铺多少米?
Bye-bye!
