2020年秋苏科版七年级数学上册第5章《走进图形世界》综合能力检测卷(Word版附答案)
文档属性
| 名称 | 2020年秋苏科版七年级数学上册第5章《走进图形世界》综合能力检测卷(Word版附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 496.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-12 00:00:00 | ||
图片预览


文档简介
第5章 综合能力检测卷
时间:60分钟
满分:130分
一、选择题(每小题3分,共30分)
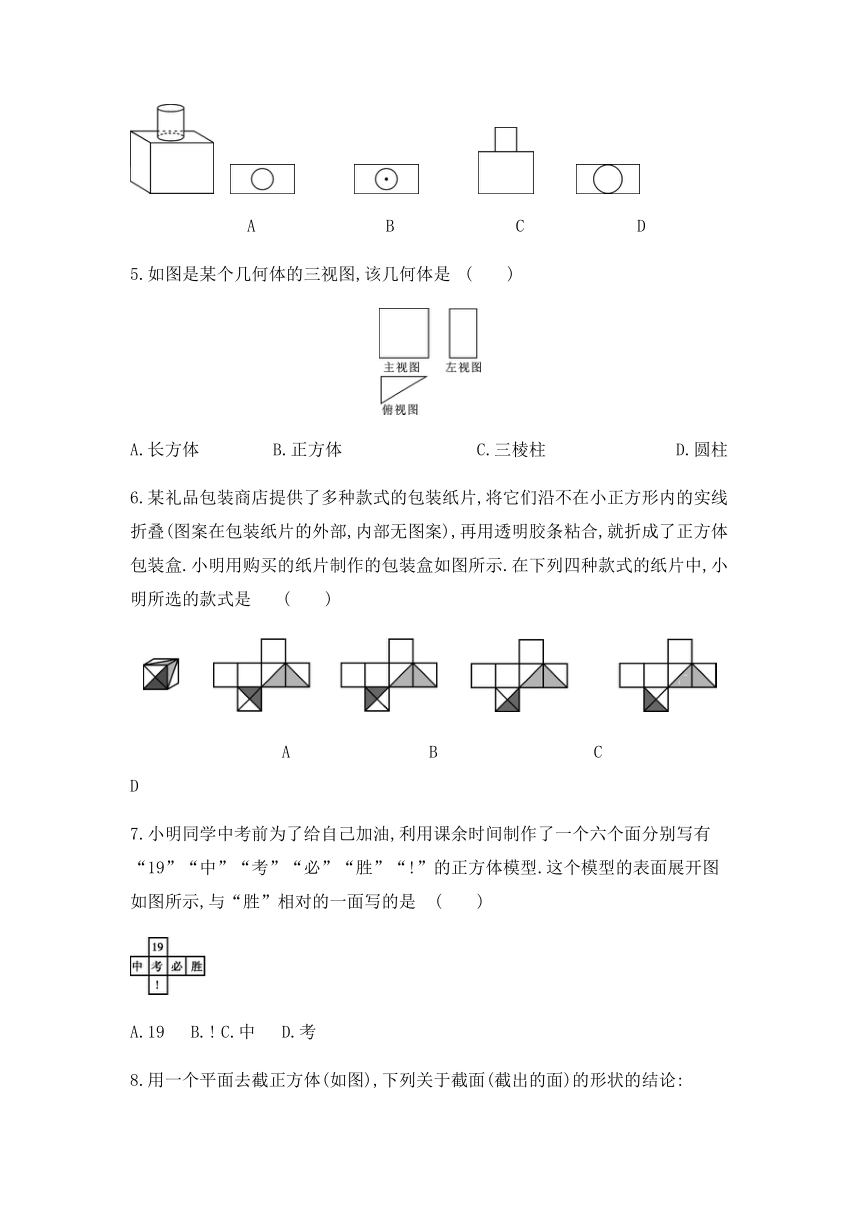
1.下列是棱柱的是
( )
A B C D
2.图中通过翻折变换得到的是
( )
A
B
C
D
3.把如图所示的图形绕着给定的直线旋转一周后形成的几何体是( )
A
B
C
D
4.如图是由长方体和圆柱组成的几何体,它的俯视图是
( )
A
B C
D
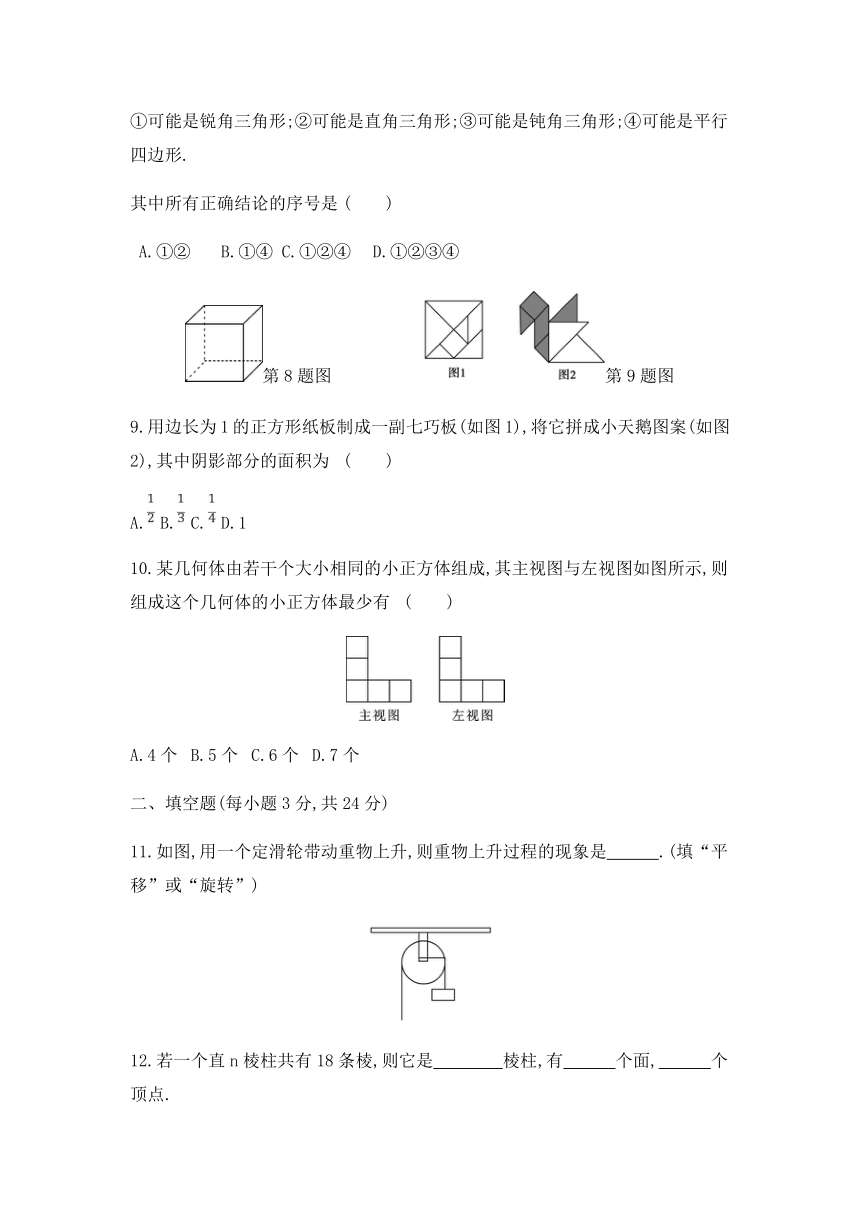
5.如图是某个几何体的三视图,该几何体是
( )
A.长方体
B.正方体
C.三棱柱
D.圆柱
6.某礼品包装商店提供了多种款式的包装纸片,将它们沿不在小正方形内的实线折叠(图案在包装纸片的外部,内部无图案),再用透明胶条粘合,就折成了正方体包装盒.小明用购买的纸片制作的包装盒如图所示.在下列四种款式的纸片中,小明所选的款式是
( )
A B C D
7.小明同学中考前为了给自己加油,利用课余时间制作了一个六个面分别写有“19”“中”“考”“必”“胜”“!”的正方体模型.这个模型的表面展开图如图所示,与“胜”相对的一面写的是
( )
A.19
B.!
C.中
D.考
8.用一个平面去截正方体(如图),下列关于截面(截出的面)的形状的结论:
①可能是锐角三角形;②可能是直角三角形;③可能是钝角三角形;④可能是平行四边形.
其中所有正确结论的序号是
( )
A.①②
B.①④
C.①②④
D.①②③④
第8题图 第9题图
9.用边长为1的正方形纸板制成一副七巧板(如图1),将它拼成小天鹅图案(如图2),其中阴影部分的面积为
( )
A.
B.
C.
D.1
10.某几何体由若干个大小相同的小正方体组成,其主视图与左视图如图所示,则组成这个几何体的小正方体最少有
( )
A.4个
B.5个
C.6个
D.7个
二、填空题(每小题3分,共24分)
11.如图,用一个定滑轮带动重物上升,则重物上升过程的现象是 .(填“平移”或“旋转”)?
12.若一个直n棱柱共有18条棱,则它是 棱柱,有 个面, 个顶点.?
13.如图是一个正方体纸盒的展开图,当折成纸盒时,与点1重合的点是 .?
14.如图所示的四个几何体中,主视图与左视图相同的几何体有 个.?
15.如图是一个长方体的三视图(单位:cm),根据图中数据计算这个长方体的体积是 cm3.?
第15题图 第16题图
16.有一个正方体,A,B,C的对面分别是x,y,z三个字母,如图所示,将这个正方体从现有位置依此翻到第1,2,3,4,5,6格,当正方体翻到第3格时,正方体向上一面的字母是 .?
17.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 .?
18.如图是由一些棱长为1的小正方体搭成的几何体的三个视图.若在所搭几何体的基础上(不改变原几何体中小正方体的位置),继续添加相同的小正方体,搭成一个长方体,至少还需要 个小正方体,最终搭成的长方体的表面积是 .?
三、解答题(共76分)
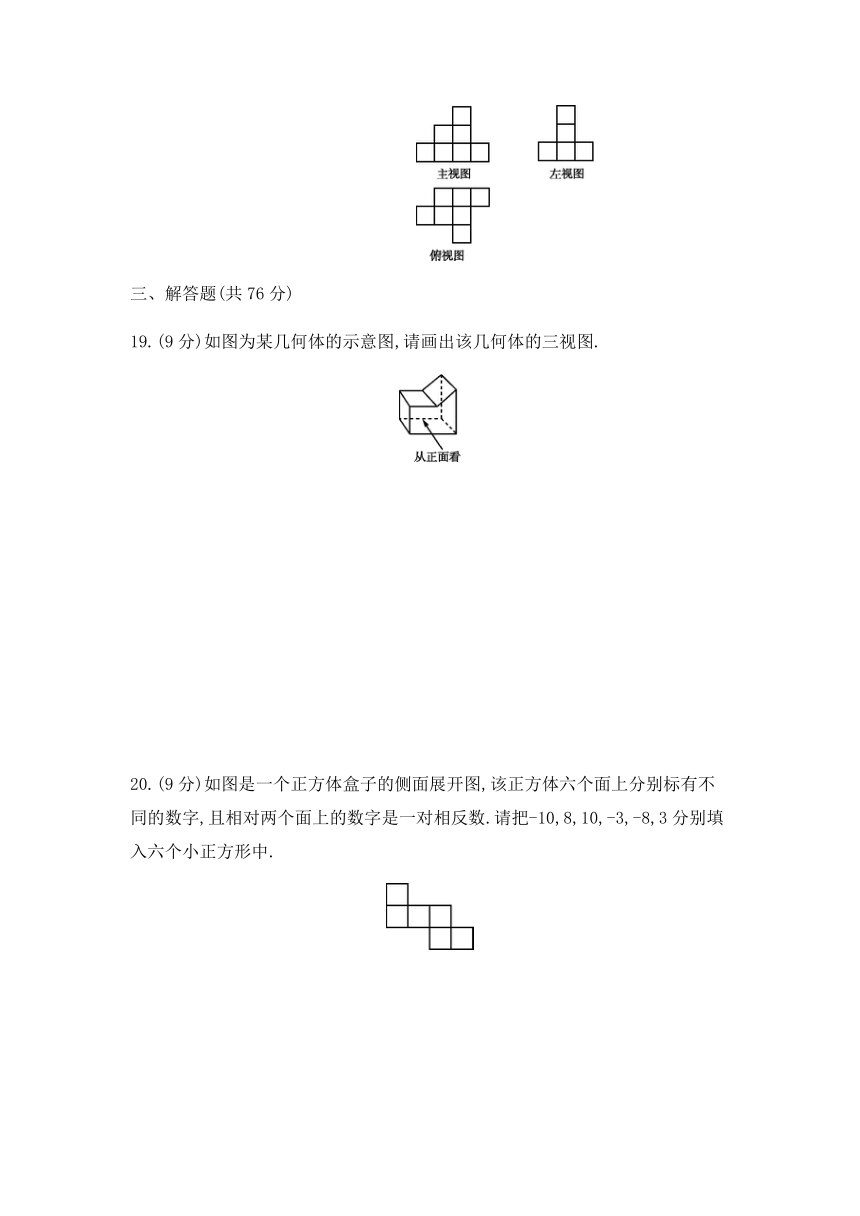
19.(9分)如图为某几何体的示意图,请画出该几何体的三视图.
20.(9分)如图是一个正方体盒子的侧面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字是一对相反数.请把-10,8,10,-3,-8,3分别填入六个小正方形中.
21.(10分)如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你在展开图中画出蚂蚁爬行的最短路线.
22.
(10分)如图是一个大正方体切去一个小正方体组成的几何体.
(1)从上面、左面、正面看到的平面图形分别是 、 、 ;?
(2)若大正方体的边长为20
cm,求这个几何体的表面积.
23.(12分)小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀剪开了一个如图1所示的长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分①,②,如图2所示.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 条棱.?
(2)如图2,现在小明想将剪掉的②重新粘贴到①上去,而且经过折叠,仍然可以还原成一个长方体纸盒,你认为他应该将剪掉的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(画出一种情况即可)
(3)小明说他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880
cm,求这个长方体纸盒的表面积.
24.(12分)(1)小明准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图1所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再画一个正方形,使新拼接的图形经过折叠后能成为一个封闭的正方体盒子;(添加的正方形用阴影表示)
(2)如图2所示的几何体是由几个相同的小正方体搭成的,请在图3中画出它的主视图;
(3)如图4是几个小正方体组成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数,请在图5中画出这个几何体的左视图.
25.(14分)将如图1所示的正方体切去一块,得到图2~5的几何体.
(1)图1~5的几何体各有多少个面?多少条棱?多少个顶点?
(2)举例说明其他形状的几何体也切去一块,所得到的几何体的面数、棱数和顶点数各是多少.
(3)若面数记为f,棱数记为e,顶点数记为v,则f+v-e应满足什么关系?
参考答案
题号
1
2
3
4
5
6
7
8
9
10
答案
A
B
D
A
C
D
D
B
A
B
11.平移 12.六 8 12 13.7和11 14.4 15.24 16.x17.144或384π 18.26 66
19.
20.
21. (1)该几何体是圆锥.
(2)线段BD或B'D即所求的最短路线.
22. (1)③ ② ①
(2)2
400(cm2).
23. (1)8
(2)
(3)①28
000(cm2).
②28
000
cm2或
cm2.
24. 略
25. (1)题图1中的正方体有6个面,12条棱,8个顶点.
题图2中的几何体有7个面,15条棱,10个顶点.
题图3中的几何体有7个面,14条棱,9个顶点.
题图4中的几何体有7个面,13条棱,8个顶点.
题图5中的几何体有7个面,12条棱,7个顶点.
(2)
图
顶点数a
棱数b
面数c
1
8
12
6
2
6
9
5
3
8
12
6
4
8
13
7
5
10
15
7
(3)f+v-e=2.
时间:60分钟
满分:130分
一、选择题(每小题3分,共30分)
1.下列是棱柱的是
( )
A B C D
2.图中通过翻折变换得到的是
( )
A
B
C
D
3.把如图所示的图形绕着给定的直线旋转一周后形成的几何体是( )
A
B
C
D
4.如图是由长方体和圆柱组成的几何体,它的俯视图是
( )
A
B C
D
5.如图是某个几何体的三视图,该几何体是
( )
A.长方体
B.正方体
C.三棱柱
D.圆柱
6.某礼品包装商店提供了多种款式的包装纸片,将它们沿不在小正方形内的实线折叠(图案在包装纸片的外部,内部无图案),再用透明胶条粘合,就折成了正方体包装盒.小明用购买的纸片制作的包装盒如图所示.在下列四种款式的纸片中,小明所选的款式是
( )
A B C D
7.小明同学中考前为了给自己加油,利用课余时间制作了一个六个面分别写有“19”“中”“考”“必”“胜”“!”的正方体模型.这个模型的表面展开图如图所示,与“胜”相对的一面写的是
( )
A.19
B.!
C.中
D.考
8.用一个平面去截正方体(如图),下列关于截面(截出的面)的形状的结论:
①可能是锐角三角形;②可能是直角三角形;③可能是钝角三角形;④可能是平行四边形.
其中所有正确结论的序号是
( )
A.①②
B.①④
C.①②④
D.①②③④
第8题图 第9题图
9.用边长为1的正方形纸板制成一副七巧板(如图1),将它拼成小天鹅图案(如图2),其中阴影部分的面积为
( )
A.
B.
C.
D.1
10.某几何体由若干个大小相同的小正方体组成,其主视图与左视图如图所示,则组成这个几何体的小正方体最少有
( )
A.4个
B.5个
C.6个
D.7个
二、填空题(每小题3分,共24分)
11.如图,用一个定滑轮带动重物上升,则重物上升过程的现象是 .(填“平移”或“旋转”)?
12.若一个直n棱柱共有18条棱,则它是 棱柱,有 个面, 个顶点.?
13.如图是一个正方体纸盒的展开图,当折成纸盒时,与点1重合的点是 .?
14.如图所示的四个几何体中,主视图与左视图相同的几何体有 个.?
15.如图是一个长方体的三视图(单位:cm),根据图中数据计算这个长方体的体积是 cm3.?
第15题图 第16题图
16.有一个正方体,A,B,C的对面分别是x,y,z三个字母,如图所示,将这个正方体从现有位置依此翻到第1,2,3,4,5,6格,当正方体翻到第3格时,正方体向上一面的字母是 .?
17.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 .?
18.如图是由一些棱长为1的小正方体搭成的几何体的三个视图.若在所搭几何体的基础上(不改变原几何体中小正方体的位置),继续添加相同的小正方体,搭成一个长方体,至少还需要 个小正方体,最终搭成的长方体的表面积是 .?
三、解答题(共76分)
19.(9分)如图为某几何体的示意图,请画出该几何体的三视图.
20.(9分)如图是一个正方体盒子的侧面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字是一对相反数.请把-10,8,10,-3,-8,3分别填入六个小正方形中.
21.(10分)如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你在展开图中画出蚂蚁爬行的最短路线.
22.
(10分)如图是一个大正方体切去一个小正方体组成的几何体.
(1)从上面、左面、正面看到的平面图形分别是 、 、 ;?
(2)若大正方体的边长为20
cm,求这个几何体的表面积.
23.(12分)小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀剪开了一个如图1所示的长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分①,②,如图2所示.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 条棱.?
(2)如图2,现在小明想将剪掉的②重新粘贴到①上去,而且经过折叠,仍然可以还原成一个长方体纸盒,你认为他应该将剪掉的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(画出一种情况即可)
(3)小明说他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880
cm,求这个长方体纸盒的表面积.
24.(12分)(1)小明准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图1所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再画一个正方形,使新拼接的图形经过折叠后能成为一个封闭的正方体盒子;(添加的正方形用阴影表示)
(2)如图2所示的几何体是由几个相同的小正方体搭成的,请在图3中画出它的主视图;
(3)如图4是几个小正方体组成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数,请在图5中画出这个几何体的左视图.
25.(14分)将如图1所示的正方体切去一块,得到图2~5的几何体.
(1)图1~5的几何体各有多少个面?多少条棱?多少个顶点?
(2)举例说明其他形状的几何体也切去一块,所得到的几何体的面数、棱数和顶点数各是多少.
(3)若面数记为f,棱数记为e,顶点数记为v,则f+v-e应满足什么关系?
参考答案
题号
1
2
3
4
5
6
7
8
9
10
答案
A
B
D
A
C
D
D
B
A
B
11.平移 12.六 8 12 13.7和11 14.4 15.24 16.x17.144或384π 18.26 66
19.
20.
21. (1)该几何体是圆锥.
(2)线段BD或B'D即所求的最短路线.
22. (1)③ ② ①
(2)2
400(cm2).
23. (1)8
(2)
(3)①28
000(cm2).
②28
000
cm2或
cm2.
24. 略
25. (1)题图1中的正方体有6个面,12条棱,8个顶点.
题图2中的几何体有7个面,15条棱,10个顶点.
题图3中的几何体有7个面,14条棱,9个顶点.
题图4中的几何体有7个面,13条棱,8个顶点.
题图5中的几何体有7个面,12条棱,7个顶点.
(2)
图
顶点数a
棱数b
面数c
1
8
12
6
2
6
9
5
3
8
12
6
4
8
13
7
5
10
15
7
(3)f+v-e=2.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
