六年级下册数学试题-第13周图形的认识与测量周测卷(含答案)人教版
文档属性
| 名称 | 六年级下册数学试题-第13周图形的认识与测量周测卷(含答案)人教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 340.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-12 21:23:54 | ||
图片预览

文档简介
六年级
第13周
一级监测卷
监测内容:
图形的认识与测量
时间:40分钟
满分100分
一、填一填。(每空2分,共32分)
1.在括号里填上适当的计量单位。
①爸爸的身高是175(
)。
②一间教室的面积是48(
)。
③一瓶矿泉水大约有375(
)。
④一个集装箱的容积是24(
)。
2.经过一点可以画出(
)条直线,经过两点可以画出(
)条直线。
3.一个平行四边形,底是12cm,高是6cm,面积是(
)cm2,与它等底等高的三角形的面积是(
)cm2。
4.一个三角形三个内角的度数的比为7∶3∶2,这个三角形最大的角是(
)度,它是一个(
)三角形。
5.3个棱长是1cm的正方体摆成1个长方体,这个长方体的表面积是(
)cm2,体积
是(
)cm3。
6.一个正方体铁块的棱长总和是48cm,它的表面积是(
)cm2,体积是(
)cm3,
若将它铸造成底面积是32cm2的圆锥,则圆锥的高是(
)cm。
7.把一个棱长是8dm的正方体削成一个最大的圆锥,这个圆锥的体积是(
)dm3。
二、辨一辨。(对的画“√”,错的画“×”)(共10分)
1.钟面上3时或9时,时针和分针所形成的角是直角。
(
)
2.面积相等的两个三角形一定可以拼成一个平行四边形。
(
)
3.长度分别为6cm,3cm,2cm的三根小棒能围成一个三角形。
(
)
4.一个圆柱与一个圆锥等底等高,圆柱的体积是圆锥的3倍。
(
)
5.圆柱的底面直径扩大2倍,它的周长和面积都扩大2倍。
(
)
三、选择。(把正确答案的序号填在括号里)(每空3分,共9分)
1、右图中∠1=(
),∠2=(
)。
A.30°
B.
50°
C.60°
2、如图,每个小正方形的面积为1cm2,阴影部分的面积是(
)cm2。
A.40
B.
32
C.36
右图所示是一个盛了水的长方体容器,它的底面是一个边长10cm的正方形。老师把两个体积均是7.5cm3的金属球浸没在容器的水里,容器里的水位上升了(
)cm。
A.
0.15
B.
1.5
C.
15
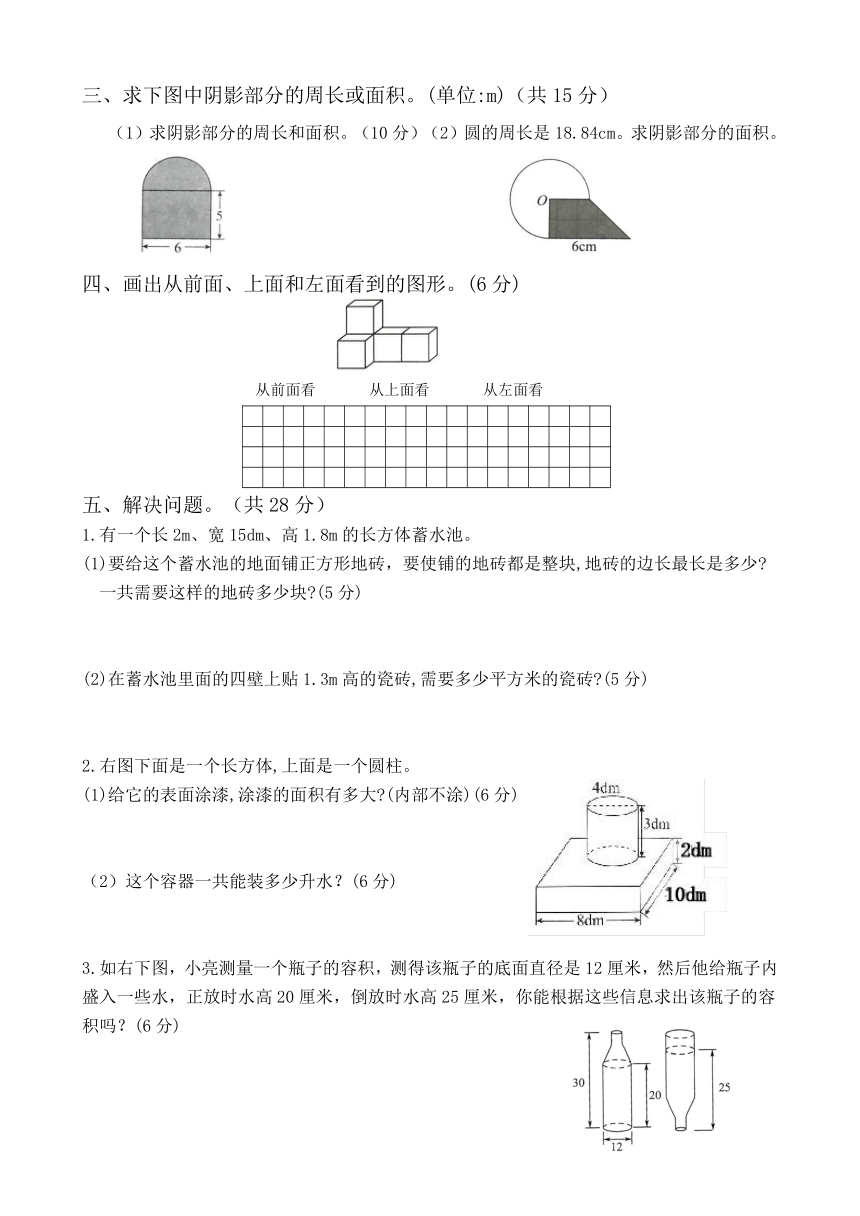
三、求下图中阴影部分的周长或面积。(单位:m)(共15分)
(1)求阴影部分的周长和面积。(10分)(2)圆的周长是18.84cm。求阴影部分的面积。
四、画出从前面、上面和左面看到的图形。(6分)
从前面看
从上面看
从左面看
五、解决问题。(共28分)
1.有一个长2m、宽15dm、高1.8m的长方体蓄水池。
(1)要给这个蓄水池的地面铺正方形地砖,要使铺的地砖都是整块,地砖的边长最长是多少?一共需要这样的地砖多少块?(5分)
(2)在蓄水池里面的四壁上贴1.3m高的瓷砖,需要多少平方米的瓷砖?(5分)
2.右图下面是一个长方体,上面是一个圆柱。
(1)给它的表面涂漆,涂漆的面积有多大?(内部不涂)(6分)
(2)这个容器一共能装多少升水?(6分)
3.如右下图,小亮测量一个瓶子的容积,测得该瓶子的底面直径是12厘米,然后他给瓶子内盛入一些水,正放时水高20厘米,倒放时水高25厘米,你能根据这些信息求出该瓶子的容积吗?(6分)
六年级
第13周
二级监测卷
监测内容:
图形的认识与测量
时间:40分钟
满分100分
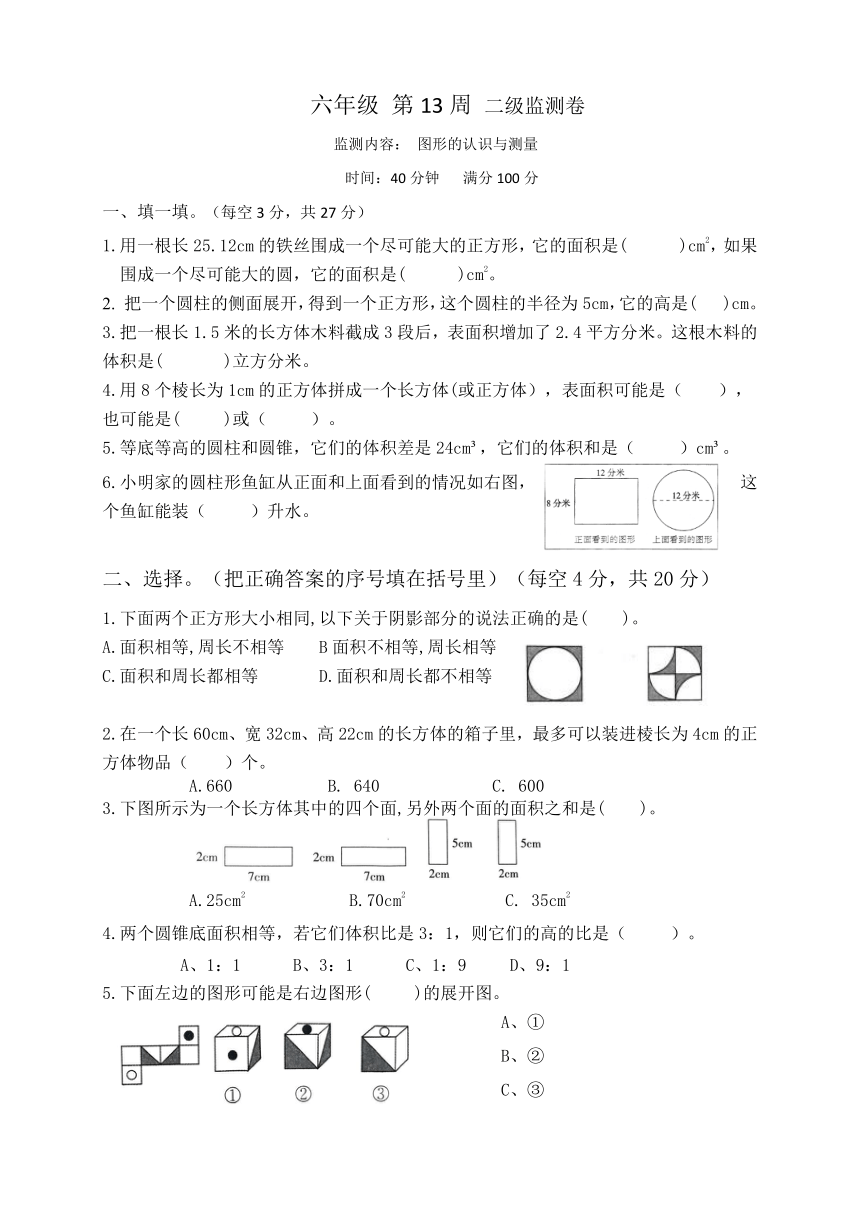
一、填一填。(每空3分,共27分)
1.用一根长25.12cm的铁丝围成一个尽可能大的正方形,它的面积是(
)cm2,如果围成一个尽可能大的圆,它的面积是(
)cm2。
2.
把一个圆柱的侧面展开,得到一个正方形,这个圆柱的半径为5cm,它的高是(
)cm。
3.把一根长1.5米的长方体木料截成3段后,表面积增加了2.4平方分米。这根木料的体积是(
)立方分米。
4.用8个棱长为1cm的正方体拼成一个长方体(或正方体),表面积可能是(
),也可能是(
)或(
)。
5.等底等高的圆柱和圆锥,它们的体积差是24cm?,它们的体积和是(
)cm?。
6.小明家的圆柱形鱼缸从正面和上面看到的情况如右图,这个鱼缸能装(
)升水。
二、选择。(把正确答案的序号填在括号里)(每空4分,共20分)
1.下面两个正方形大小相同,以下关于阴影部分的说法正确的是(
)。
A.面积相等,周长不相等
B面积不相等,周长相等
C.面积和周长都相等
D.面积和周长都不相等
2.在一个长60cm、宽32cm、高22cm的长方体的箱子里,最多可以装进棱长为4cm的正方体物品(
)个。
A.660
B.
640
C.
600
3.下图所示为一个长方体其中的四个面,另外两个面的面积之和是(
)。
A.25cm2
B.70cm2
C.
35cm2
4.两个圆锥底面积相等,若它们体积比是3:1,则它们的高的比是(
)。
A、1:1
B、3:1
C、1:9
D、9:1
5.下面左边的图形可能是右边图形(
)的展开图。
A、①
B、②
C、③
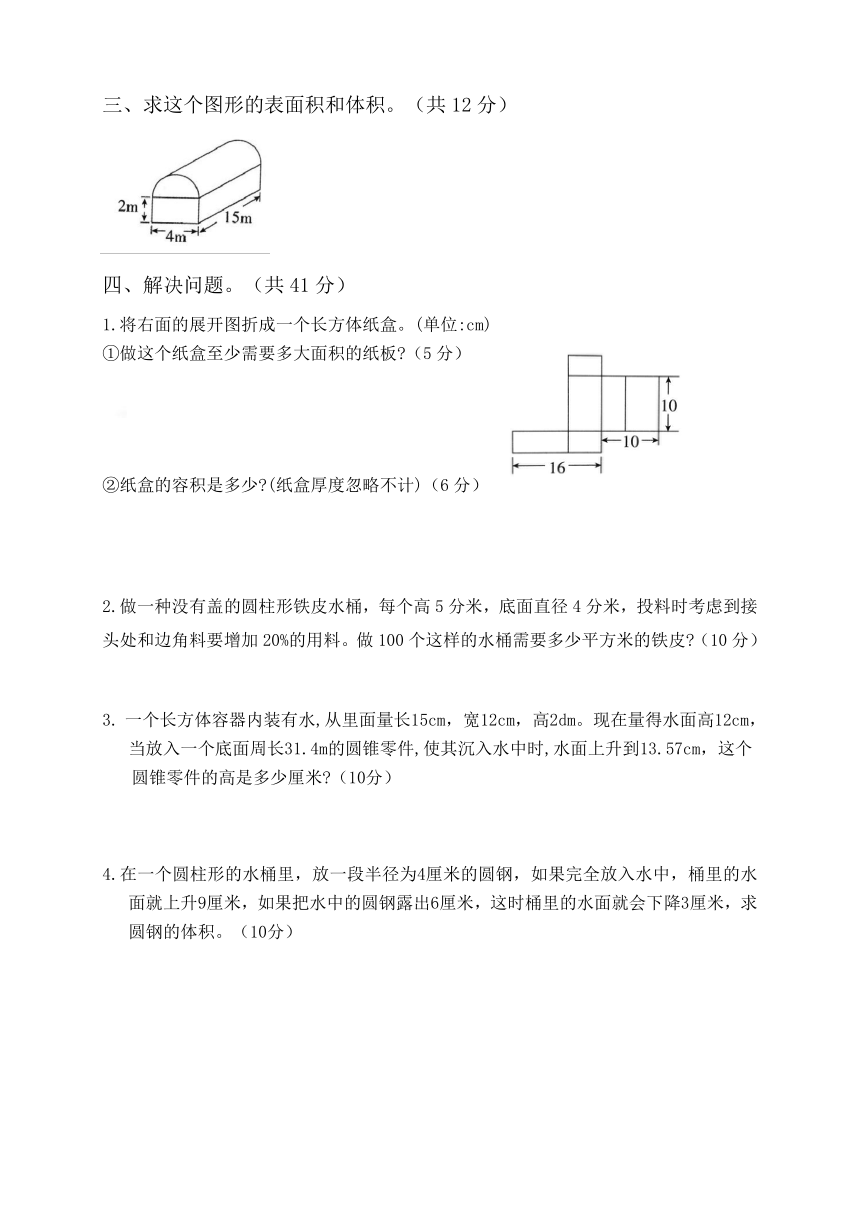
三、求这个图形的表面积和体积。(共12分)
解决问题。(共41分)
1.将右面的展开图折成一个长方体纸盒。(单位:cm)
①做这个纸盒至少需要多大面积的纸板?(5分)
②纸盒的容积是多少?(纸盒厚度忽略不计)(6分)
2.做一种没有盖的圆柱形铁皮水桶,每个高5分米,底面直径4分米,投料时考虑到接头处和边角料要增加20%的用料。做100个这样的水桶需要多少平方米的铁皮?(10分)
一个长方体容器内装有水,从里面量长15cm,宽12cm,高2dm。现在量得水面高12cm,当放入一个底面周长31.4m的圆锥零件,使其沉入水中时,水面上升到13.57cm,这个
圆锥零件的高是多少厘米?(10分)
4.在一个圆柱形的水桶里,放一段半径为4厘米的圆钢,如果完全放入水中,桶里的水面就上升9厘米,如果把水中的圆钢露出6厘米,这时桶里的水面就会下降3厘米,求圆钢的体积。(10分)
六年级
第13周
一级监测卷参考答案
监测内容:
图形的认识与测量
时间:40分钟
满分100分
一、填一填。(每空2分,共32分)
1.在括号里填上适当的计量单位。
①爸爸的身高是175(厘米)。
②一间教室的面积是48(
平方米
)。
③一瓶矿泉水大约有375(
毫升
)。
④一个集装箱的容积是24(立方米)。
2.经过一点可以画出(无数
)条直线,经过两点可以画出(一)条直线。
3.一个平行四边形,底是12cm,高是6cm,面积是(
72
)cm2,与它等底等高的三角形的面积是(
36
)cm2。
4.一个三角形三个内角的度数的比为7∶3∶2,这个三角形最大的角是(105)度,它是一个(钝角)三角形。
5.3个棱长是1cm的正方体摆成1个长方体,这个长方体的表面积是(
14
)cm2,体积
是(
3
)cm3。
6.一个正方体铁块的棱长总和是48cm,它的表面积是(
96
)cm2,体积是(
64
)cm3,
若将它铸造成底面积是32cm2的圆锥,则圆锥的高是(
6
)cm。
7.把一个棱长是6dm的正方体削成一个最大的圆锥,这个圆锥的体积是(
56.52
)dm3。
二、辨一辨。(对的画“√”,错的画“×”)(共10分)
1.钟面上3时或9时,时针和分针所形成的角是直角。
(
√
)
2.面积相等的两个三角形一定可以拼成一个平行四边形。
(
×
)
3.长度分别为6cm,3cm,2cm的三根小棒能围成一个三角形。
(
×
)
4.一个圆柱与一个圆锥等底等高,圆柱的体积是圆锥的3倍。
(
√
)
5.圆柱的底面直径扩大2倍,它的周长和面积都扩大2倍。
(
×
)
三、选择。(把正确答案的序号填在括号里)(每空3分,共9分)
1、右图中∠1=(
A
),∠2=(
C
)。
A.30°
B.
50°
C.60°
2、如图,每个小正方形的面积为1cm2,阴影部分的面积是(
B
)cm2。
A.40
B.
32
C.36
3.右图所示是一个盛了水的长方体容器,它的底面是一个边长10cm的正方形。老师把两个体积均是7.5cm3的金属球浸没在容器的水里,容器里的水位上升了(
A
)cm。
A.
0.15
B.
1.5
C.
15
三、求下图中阴影部分的周长或面积。(单位:m)(共15分)
(1)求阴影部分的周长和面积。(10分)
(2)圆的周长是18.84cm。求阴影部分的面积。
四、画出从前面、上面和左面看到的图形。(6分)
从前面看
从上面看
从左面看
五、解决问题。(共28分)
1.有一个长2m、宽15dm、高1.8m的长方体蓄水池。
(1)要给这个蓄水池的地面铺正方形地砖,要使铺的地砖都是整块,地砖的边长最长是多少?一共需要这样的地砖多少块?(5分)
2m=20dm
求地砖的边长最长是多少,就是求20和15的最大公因数,20和15的最大公因数是5,说明地砖的边长最长是5dm。
(20×15)÷(5×5)=12(块)
答:地砖的边长最长是5dm,一共需要这样的地砖12块。
(2)在蓄水池里面的四壁上贴1.3m高的瓷砖,需要多少平方米的瓷砖?(5分)
15dm=1.5m
2×1.5+(2×1.3+1.3×1.5)×2=12.1(平方米)
答:需要12.1平方米的瓷砖。
2.右图下面是一个长方体,上面是一个圆柱。
(1)给它的表面涂漆,涂漆的面积有多大?(内部不涂)(6分)
4×3.14×3+(8×10+8×2+10×2)×2=269.68(dm2)
答:涂漆的面积是269.68dm2。
(2)这个容器一共能装多少升水?(6分)
(4÷2)2×3.14×3+8×10×2=197.68(dm3)=197.68L
答:这个容器一共能装197.68L水。
3.如右下图,小亮测量一个瓶子的容积,测得该瓶子的底面直径是12厘米,然后他给瓶子内盛入一些水,正放时水高20厘米,倒放时水高25厘米,你能根据这些信息求出该瓶子的容积吗?(6分)
(12÷2)2×3.14×(20+30-25)=2826(cm
3)
答:该瓶子的容积是2826cm
3。
六年级
第13周
二级监测卷参考答案
监测内容:
图形的认识与测量
时间:40分钟
满分100分
一、填一填。(每空3分,共27分)
1.用一根长25.12cm的铁丝围成一个尽可能大的正方形,它的面积是(
39.4384
)cm2,如果围成一个尽可能大的圆,它的面积是(50.24)cm2。
2.
把一个圆柱的侧面展开,得到一个正方形,这个圆柱的半径为5cm,它的高是(31.4)cm。
3.把一根长1.5米的长方体木料截成3段后,表面积增加了32.4平方分米。这根木料的体积是(
1.215
)立方分米。
4.用8个棱长为1cm的正方体拼成一个长方体(或正方体),表面积可能是(24cm2
),也可能是(
28cm2
)或(
34cm2
)。
5.等底等高的圆柱和圆锥,它们的体积差是24cm?,它们的体积和是(48
)cm?。
6.小明家的圆柱形鱼缸从正面和上面看到的情况如右图,这个鱼缸能装(904.32
)升水。
二、选择。(把正确答案的序号填在括号里)(每空4分,共20分)
1.下面两个正方形大小相同,以下关于阴影部分的说法正确的是(
C
)。
A.面积相等,周长不相等
B面积不相等,周长相等
C.面积和周长都相等
D.面积和周长都不相等
2.在一个长60cm、宽32cm、高22cm的长方体的箱子里,最多可以装进棱长为4cm的正方体物品(
C
)个。
A.660
B.
640
C.
600
3.下图所示为一个长方体其中的四个面,另外两个面的面积之和是(
B
)。
A.25cm2
B.70cm2
C.
35cm2
4.两个圆锥底面积相等,若它们体积比是3:1,则它们的高的比是(
B
)。
A、1:1
B、3:1
C、1:9
D、9:1
5.下面左边的图形可能是右边图形(
B
)的展开图。
A、①
B、②
C、③
三、求这个图形的表面积和体积。(共12分)
(4×2+2×15)×2+15×4+3.14×(4÷2)2+3.14×4×15×=242.76(m2)
2×4×15+3.14×(4÷2)2×15×=214.2(m3)
四、解决问题。(共41分)
1.将右面的展开图折成一个长方体纸盒。(单位:cm)
①做这个纸盒至少需要多大面积的纸板?(5分)
长:10cm
宽:16-10=6(cm)
高:10-6=4(cm)
(6×10+10×4+4×6)×2=248(cm2)
答:做这个纸盒至少需要248cm2的纸板。
②纸盒的容积是多少?(纸盒厚度忽略不计)(6分)
10×6×4=240(cm3)
答:纸盒的容积是240立方厘米。
2.做一种没有盖的圆柱形铁皮水桶,每个高5分米,底面直径4分米,投料时考虑到接头处和边角料要增加20%的用料。做100个这样的水桶需要多少平方米的铁皮?(10分)
[(4÷2)2×3.14+4×3.14×5]×100×(1+20%)=9043.2(m2)
答:做100个这样的水桶需要9043.2平方米的铁皮。
3.一个长方体容器内装有水,从里面量长15cm,宽12cm,高2dm。现在量得水面高12cm,当放入一个底面周长31.4m的圆锥零件,使其沉入水中时,水面上升到13.57cm,这个圆锥零件的高是多少厘米?(10分)
圆锥的半径:
31.4÷3.14÷2=5(m)
[(13.57-12)×15×12×3)]÷(52×3.14)=10.8(厘米)
答:这个圆锥零件的高是10.8厘米。
4.在一个圆柱形的水桶里,放一段半径为4厘米的圆钢,如果完全放入水中,桶里的水面就上升9厘米,如果把水中的圆钢露出6厘米,这时桶里的水面就会下降3厘米,求圆钢的体积。(10分)
方法一:6厘米长的圆钢体积=水桶的底面积×3厘米
水桶的底面积:(3.14×42×6)÷3=100.48(平方厘米)
圆钢的体积为:100.48×9=904.32(立方厘米)
方法二:圆钢露出6厘米,水面下降3厘米,圆钢全部露出,水面就会下降9厘米,可以求出圆钢的高。
6×(9÷3)=18(厘米)
圆钢的体积为:3.14×42×18=904.32(立方厘米)
答:圆钢的体积为904.32立方厘米。
第13周
一级监测卷
监测内容:
图形的认识与测量
时间:40分钟
满分100分
一、填一填。(每空2分,共32分)
1.在括号里填上适当的计量单位。
①爸爸的身高是175(
)。
②一间教室的面积是48(
)。
③一瓶矿泉水大约有375(
)。
④一个集装箱的容积是24(
)。
2.经过一点可以画出(
)条直线,经过两点可以画出(
)条直线。
3.一个平行四边形,底是12cm,高是6cm,面积是(
)cm2,与它等底等高的三角形的面积是(
)cm2。
4.一个三角形三个内角的度数的比为7∶3∶2,这个三角形最大的角是(
)度,它是一个(
)三角形。
5.3个棱长是1cm的正方体摆成1个长方体,这个长方体的表面积是(
)cm2,体积
是(
)cm3。
6.一个正方体铁块的棱长总和是48cm,它的表面积是(
)cm2,体积是(
)cm3,
若将它铸造成底面积是32cm2的圆锥,则圆锥的高是(
)cm。
7.把一个棱长是8dm的正方体削成一个最大的圆锥,这个圆锥的体积是(
)dm3。
二、辨一辨。(对的画“√”,错的画“×”)(共10分)
1.钟面上3时或9时,时针和分针所形成的角是直角。
(
)
2.面积相等的两个三角形一定可以拼成一个平行四边形。
(
)
3.长度分别为6cm,3cm,2cm的三根小棒能围成一个三角形。
(
)
4.一个圆柱与一个圆锥等底等高,圆柱的体积是圆锥的3倍。
(
)
5.圆柱的底面直径扩大2倍,它的周长和面积都扩大2倍。
(
)
三、选择。(把正确答案的序号填在括号里)(每空3分,共9分)
1、右图中∠1=(
),∠2=(
)。
A.30°
B.
50°
C.60°
2、如图,每个小正方形的面积为1cm2,阴影部分的面积是(
)cm2。
A.40
B.
32
C.36
右图所示是一个盛了水的长方体容器,它的底面是一个边长10cm的正方形。老师把两个体积均是7.5cm3的金属球浸没在容器的水里,容器里的水位上升了(
)cm。
A.
0.15
B.
1.5
C.
15
三、求下图中阴影部分的周长或面积。(单位:m)(共15分)
(1)求阴影部分的周长和面积。(10分)(2)圆的周长是18.84cm。求阴影部分的面积。
四、画出从前面、上面和左面看到的图形。(6分)
从前面看
从上面看
从左面看
五、解决问题。(共28分)
1.有一个长2m、宽15dm、高1.8m的长方体蓄水池。
(1)要给这个蓄水池的地面铺正方形地砖,要使铺的地砖都是整块,地砖的边长最长是多少?一共需要这样的地砖多少块?(5分)
(2)在蓄水池里面的四壁上贴1.3m高的瓷砖,需要多少平方米的瓷砖?(5分)
2.右图下面是一个长方体,上面是一个圆柱。
(1)给它的表面涂漆,涂漆的面积有多大?(内部不涂)(6分)
(2)这个容器一共能装多少升水?(6分)
3.如右下图,小亮测量一个瓶子的容积,测得该瓶子的底面直径是12厘米,然后他给瓶子内盛入一些水,正放时水高20厘米,倒放时水高25厘米,你能根据这些信息求出该瓶子的容积吗?(6分)
六年级
第13周
二级监测卷
监测内容:
图形的认识与测量
时间:40分钟
满分100分
一、填一填。(每空3分,共27分)
1.用一根长25.12cm的铁丝围成一个尽可能大的正方形,它的面积是(
)cm2,如果围成一个尽可能大的圆,它的面积是(
)cm2。
2.
把一个圆柱的侧面展开,得到一个正方形,这个圆柱的半径为5cm,它的高是(
)cm。
3.把一根长1.5米的长方体木料截成3段后,表面积增加了2.4平方分米。这根木料的体积是(
)立方分米。
4.用8个棱长为1cm的正方体拼成一个长方体(或正方体),表面积可能是(
),也可能是(
)或(
)。
5.等底等高的圆柱和圆锥,它们的体积差是24cm?,它们的体积和是(
)cm?。
6.小明家的圆柱形鱼缸从正面和上面看到的情况如右图,这个鱼缸能装(
)升水。
二、选择。(把正确答案的序号填在括号里)(每空4分,共20分)
1.下面两个正方形大小相同,以下关于阴影部分的说法正确的是(
)。
A.面积相等,周长不相等
B面积不相等,周长相等
C.面积和周长都相等
D.面积和周长都不相等
2.在一个长60cm、宽32cm、高22cm的长方体的箱子里,最多可以装进棱长为4cm的正方体物品(
)个。
A.660
B.
640
C.
600
3.下图所示为一个长方体其中的四个面,另外两个面的面积之和是(
)。
A.25cm2
B.70cm2
C.
35cm2
4.两个圆锥底面积相等,若它们体积比是3:1,则它们的高的比是(
)。
A、1:1
B、3:1
C、1:9
D、9:1
5.下面左边的图形可能是右边图形(
)的展开图。
A、①
B、②
C、③
三、求这个图形的表面积和体积。(共12分)
解决问题。(共41分)
1.将右面的展开图折成一个长方体纸盒。(单位:cm)
①做这个纸盒至少需要多大面积的纸板?(5分)
②纸盒的容积是多少?(纸盒厚度忽略不计)(6分)
2.做一种没有盖的圆柱形铁皮水桶,每个高5分米,底面直径4分米,投料时考虑到接头处和边角料要增加20%的用料。做100个这样的水桶需要多少平方米的铁皮?(10分)
一个长方体容器内装有水,从里面量长15cm,宽12cm,高2dm。现在量得水面高12cm,当放入一个底面周长31.4m的圆锥零件,使其沉入水中时,水面上升到13.57cm,这个
圆锥零件的高是多少厘米?(10分)
4.在一个圆柱形的水桶里,放一段半径为4厘米的圆钢,如果完全放入水中,桶里的水面就上升9厘米,如果把水中的圆钢露出6厘米,这时桶里的水面就会下降3厘米,求圆钢的体积。(10分)
六年级
第13周
一级监测卷参考答案
监测内容:
图形的认识与测量
时间:40分钟
满分100分
一、填一填。(每空2分,共32分)
1.在括号里填上适当的计量单位。
①爸爸的身高是175(厘米)。
②一间教室的面积是48(
平方米
)。
③一瓶矿泉水大约有375(
毫升
)。
④一个集装箱的容积是24(立方米)。
2.经过一点可以画出(无数
)条直线,经过两点可以画出(一)条直线。
3.一个平行四边形,底是12cm,高是6cm,面积是(
72
)cm2,与它等底等高的三角形的面积是(
36
)cm2。
4.一个三角形三个内角的度数的比为7∶3∶2,这个三角形最大的角是(105)度,它是一个(钝角)三角形。
5.3个棱长是1cm的正方体摆成1个长方体,这个长方体的表面积是(
14
)cm2,体积
是(
3
)cm3。
6.一个正方体铁块的棱长总和是48cm,它的表面积是(
96
)cm2,体积是(
64
)cm3,
若将它铸造成底面积是32cm2的圆锥,则圆锥的高是(
6
)cm。
7.把一个棱长是6dm的正方体削成一个最大的圆锥,这个圆锥的体积是(
56.52
)dm3。
二、辨一辨。(对的画“√”,错的画“×”)(共10分)
1.钟面上3时或9时,时针和分针所形成的角是直角。
(
√
)
2.面积相等的两个三角形一定可以拼成一个平行四边形。
(
×
)
3.长度分别为6cm,3cm,2cm的三根小棒能围成一个三角形。
(
×
)
4.一个圆柱与一个圆锥等底等高,圆柱的体积是圆锥的3倍。
(
√
)
5.圆柱的底面直径扩大2倍,它的周长和面积都扩大2倍。
(
×
)
三、选择。(把正确答案的序号填在括号里)(每空3分,共9分)
1、右图中∠1=(
A
),∠2=(
C
)。
A.30°
B.
50°
C.60°
2、如图,每个小正方形的面积为1cm2,阴影部分的面积是(
B
)cm2。
A.40
B.
32
C.36
3.右图所示是一个盛了水的长方体容器,它的底面是一个边长10cm的正方形。老师把两个体积均是7.5cm3的金属球浸没在容器的水里,容器里的水位上升了(
A
)cm。
A.
0.15
B.
1.5
C.
15
三、求下图中阴影部分的周长或面积。(单位:m)(共15分)
(1)求阴影部分的周长和面积。(10分)
(2)圆的周长是18.84cm。求阴影部分的面积。
四、画出从前面、上面和左面看到的图形。(6分)
从前面看
从上面看
从左面看
五、解决问题。(共28分)
1.有一个长2m、宽15dm、高1.8m的长方体蓄水池。
(1)要给这个蓄水池的地面铺正方形地砖,要使铺的地砖都是整块,地砖的边长最长是多少?一共需要这样的地砖多少块?(5分)
2m=20dm
求地砖的边长最长是多少,就是求20和15的最大公因数,20和15的最大公因数是5,说明地砖的边长最长是5dm。
(20×15)÷(5×5)=12(块)
答:地砖的边长最长是5dm,一共需要这样的地砖12块。
(2)在蓄水池里面的四壁上贴1.3m高的瓷砖,需要多少平方米的瓷砖?(5分)
15dm=1.5m
2×1.5+(2×1.3+1.3×1.5)×2=12.1(平方米)
答:需要12.1平方米的瓷砖。
2.右图下面是一个长方体,上面是一个圆柱。
(1)给它的表面涂漆,涂漆的面积有多大?(内部不涂)(6分)
4×3.14×3+(8×10+8×2+10×2)×2=269.68(dm2)
答:涂漆的面积是269.68dm2。
(2)这个容器一共能装多少升水?(6分)
(4÷2)2×3.14×3+8×10×2=197.68(dm3)=197.68L
答:这个容器一共能装197.68L水。
3.如右下图,小亮测量一个瓶子的容积,测得该瓶子的底面直径是12厘米,然后他给瓶子内盛入一些水,正放时水高20厘米,倒放时水高25厘米,你能根据这些信息求出该瓶子的容积吗?(6分)
(12÷2)2×3.14×(20+30-25)=2826(cm
3)
答:该瓶子的容积是2826cm
3。
六年级
第13周
二级监测卷参考答案
监测内容:
图形的认识与测量
时间:40分钟
满分100分
一、填一填。(每空3分,共27分)
1.用一根长25.12cm的铁丝围成一个尽可能大的正方形,它的面积是(
39.4384
)cm2,如果围成一个尽可能大的圆,它的面积是(50.24)cm2。
2.
把一个圆柱的侧面展开,得到一个正方形,这个圆柱的半径为5cm,它的高是(31.4)cm。
3.把一根长1.5米的长方体木料截成3段后,表面积增加了32.4平方分米。这根木料的体积是(
1.215
)立方分米。
4.用8个棱长为1cm的正方体拼成一个长方体(或正方体),表面积可能是(24cm2
),也可能是(
28cm2
)或(
34cm2
)。
5.等底等高的圆柱和圆锥,它们的体积差是24cm?,它们的体积和是(48
)cm?。
6.小明家的圆柱形鱼缸从正面和上面看到的情况如右图,这个鱼缸能装(904.32
)升水。
二、选择。(把正确答案的序号填在括号里)(每空4分,共20分)
1.下面两个正方形大小相同,以下关于阴影部分的说法正确的是(
C
)。
A.面积相等,周长不相等
B面积不相等,周长相等
C.面积和周长都相等
D.面积和周长都不相等
2.在一个长60cm、宽32cm、高22cm的长方体的箱子里,最多可以装进棱长为4cm的正方体物品(
C
)个。
A.660
B.
640
C.
600
3.下图所示为一个长方体其中的四个面,另外两个面的面积之和是(
B
)。
A.25cm2
B.70cm2
C.
35cm2
4.两个圆锥底面积相等,若它们体积比是3:1,则它们的高的比是(
B
)。
A、1:1
B、3:1
C、1:9
D、9:1
5.下面左边的图形可能是右边图形(
B
)的展开图。
A、①
B、②
C、③
三、求这个图形的表面积和体积。(共12分)
(4×2+2×15)×2+15×4+3.14×(4÷2)2+3.14×4×15×=242.76(m2)
2×4×15+3.14×(4÷2)2×15×=214.2(m3)
四、解决问题。(共41分)
1.将右面的展开图折成一个长方体纸盒。(单位:cm)
①做这个纸盒至少需要多大面积的纸板?(5分)
长:10cm
宽:16-10=6(cm)
高:10-6=4(cm)
(6×10+10×4+4×6)×2=248(cm2)
答:做这个纸盒至少需要248cm2的纸板。
②纸盒的容积是多少?(纸盒厚度忽略不计)(6分)
10×6×4=240(cm3)
答:纸盒的容积是240立方厘米。
2.做一种没有盖的圆柱形铁皮水桶,每个高5分米,底面直径4分米,投料时考虑到接头处和边角料要增加20%的用料。做100个这样的水桶需要多少平方米的铁皮?(10分)
[(4÷2)2×3.14+4×3.14×5]×100×(1+20%)=9043.2(m2)
答:做100个这样的水桶需要9043.2平方米的铁皮。
3.一个长方体容器内装有水,从里面量长15cm,宽12cm,高2dm。现在量得水面高12cm,当放入一个底面周长31.4m的圆锥零件,使其沉入水中时,水面上升到13.57cm,这个圆锥零件的高是多少厘米?(10分)
圆锥的半径:
31.4÷3.14÷2=5(m)
[(13.57-12)×15×12×3)]÷(52×3.14)=10.8(厘米)
答:这个圆锥零件的高是10.8厘米。
4.在一个圆柱形的水桶里,放一段半径为4厘米的圆钢,如果完全放入水中,桶里的水面就上升9厘米,如果把水中的圆钢露出6厘米,这时桶里的水面就会下降3厘米,求圆钢的体积。(10分)
方法一:6厘米长的圆钢体积=水桶的底面积×3厘米
水桶的底面积:(3.14×42×6)÷3=100.48(平方厘米)
圆钢的体积为:100.48×9=904.32(立方厘米)
方法二:圆钢露出6厘米,水面下降3厘米,圆钢全部露出,水面就会下降9厘米,可以求出圆钢的高。
6×(9÷3)=18(厘米)
圆钢的体积为:3.14×42×18=904.32(立方厘米)
答:圆钢的体积为904.32立方厘米。
