人教版初一数学下册9.1.2不等式的性质课件(第一课时 44张)
文档属性
| 名称 | 人教版初一数学下册9.1.2不等式的性质课件(第一课时 44张) |  | |
| 格式 | zip | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-13 09:54:35 | ||
图片预览







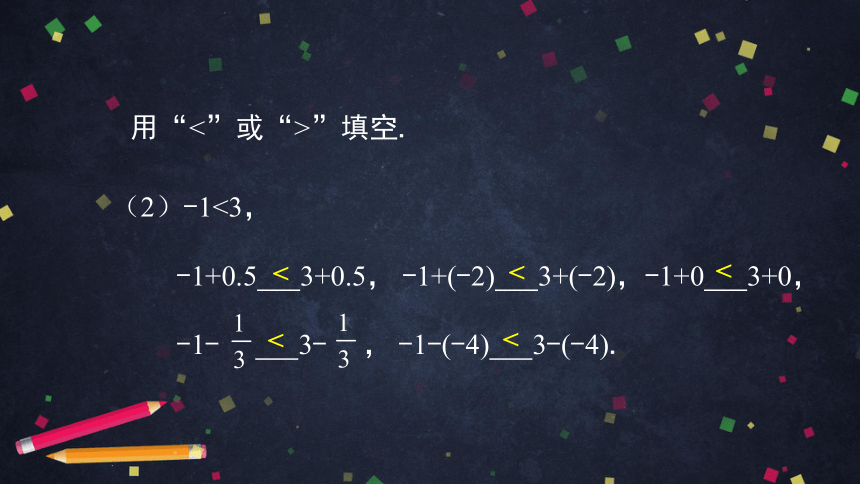




文档简介
(共44张PPT)
初一年级
数学
不等式的性质(第一课时)
不等式
不等式的解
方程的解
等式
(方程)
等式的性质
不等式的性质
(不等式的解集)
不等式
不等式的解
方程的解
等式
(方程)
等式的性质
不等式的性质
(不等式的解集)
类比
等式有哪些性质?你能分别用文字语言和符号语言表示吗?
?
文字语言
符号语言
性质1
等式两边加(或减)同一个数(或式子),结果仍相等.
如果a=b,那么a+c=b+c,a-c=b-c.
性质2
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b,那么ac=bc.
如果a=b(c≠0),那么
.
等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
不等式两边加(或减)同一个数(或式子),大小关系会发生变化吗?
用“<”或“>”填空.
(1)5>3,
5+2
3+2,5+(-
)
3+(-
),5+0
3+0,
5-0.5
3-0.5,
5-(-4)
3-(-4);
>
>
>
>
>
<
<
<
<
(2)-1<3,
-1+0.5
3+0.5,
-1+(-2)
3+(-2),-1+0
3+0,
-1-
3-
,
-1-(-4)
3-(-4).
<
用“<”或“>”填空.
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
请同学再举一些例子,验证刚才的发现.
不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
那么a+c>b+c,a-c>b-c.
如果a>b,
符号语言:
不等式两边乘(或除以)同一个数,大小关系会改变吗?
请同学们自己举例,可以选取一些数字,计算一下.
6>2,
6×3
2×3,
6×(-0.5)
2×(-0.5),
6×0
2×0;
>
比如:
>
<
<
=
=
4>-2,
4×
-2×
,
4×(-5)
-2
×(-5)
,
4×0
-2×0
;
-3>-7,
-3×0.1
-7×0.1,
-3×(-2)
-7
×(-2),
-3×0
-7×0;
>
<
=
>
<
=
0<2,
0×4
2×4,
0×(-
)
2×(-
),
0×0
2×0.
不等式两边乘同一个正数,不等号的方向不变.
如果a>b,c>0,
那么ac>bc.
6>2,
6×3
>2×3;
-3>-7,
-3×0.5>-7×0.5;
0<2,
0×4<2×4.
4>-2,
4×
>-2×
;
不等式两边乘同一个负数,不等号的方向改变.
如果a>b,c<0,
那么ac6>2,
6×(-0.5)<2×(-0.5);
4>-2,
4×(-5)
<-2
×(-5)
;
-3>-7,
-3×(-2)<-7×(-2);
0<2,
0×(-
)
>2×(-
).
4>-2,
4×0=-2×0
;
6>2,6×0=2×0;
-3>-7,
-3×0=-7×0;
0<2,
0×0=2×0.
>
<
0不能作除数.
6>-2,
6÷
-2÷
6÷(-3)
-2÷(-3)
不等式性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变.
如果a>b,c>0,
那么ac>bc(或).
不等式性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果a>b,c<0,
那么ac不等式的性质1:不等式两边加(或减)同一个数
(或式子),不等号的方向不变.
不等式的性质2:不等式两边乘(或除以)同一个
正数,不等号的方向不变.
不等式的性质3:不等式两边乘(或除以)同一个
负数,不等号的方向改变.
例
设a>b,用“<”或“>”填空,并说明依据不等式的哪条性质:
(1)a-3
b-3;
(2)10a
10b;
(3)-9a
-9b;
(4)
;
(5)-3.5a+1
-3.5b+1.
(1)a-3
b-3
(
)
(2)10a
10b
(
)
(3)-9a
-9b
(
)
>
>
<
不等式的性质1
不等式的性质2
不等式的性质3
例
设a>b,用“<”或“>”填空,并说明依据不等式的哪条性质:
-3.5a
-3.5b
(
)
-3.5a+1<-3.5b+1
(不等式的性质1)
(4)
(
)
(5)-3.5a+1
-3.5b+1(
)
不等式的性质2
>
不等式的性质3
<
<
不等式的性质1、3
例
设a>b,用“<”或“>”填空,并说明依据不等式的哪条性质:
(1)
,两边都减去2,得
;(
)
(2)
,两边都加上–5,得
;(
)
不等式性质1
不等式性质1
不等式性质1
例
根据不等式的性质填空,并说明理由:
不等式性质1
不等式性质2
不等式性质3
例
根据不等式的性质填空,并说明理由:
(3)
,两边都除以
,得
;(
)
(4)
,两边都乘
,得
.
(
)
例
根据不等式的性质填空,并说明理由:
>
(1)如果m-5>n-5,那么m
n;
(2)如果-4a
>-4b
,那么a
b
;
<
(不等式的性质1)
(不等式的性质3)
(3)如果
,那么a
b
;
(4)如果
,那么a
b
.
<
>
(不等式的性质2)
(不等式的性质3)
例
根据不等式的性质填空,并说明理由:
<
<
<
>
>
-2a>-2b
练习
已知a”填空.
(1)
a+9
b+9
;
(2)-
a
-
b;
(3)
;
(4)3a-1.7
3b-1.7
;
(5)
.
3a<3b
>
(1)如果x+36>y+36,那么x
y;
(2)如果9a
>9b
,那么a
b
;
>
(不等式的性质1)
(不等式的性质2)
练习
根据不等式的性质填空,并说明理由:
练习
根据不等式的性质填空,并说明理由:
(3)如果
,那么m
n
;
(4)如果
,那么a
b
.
<
>
(不等式的性质3)
(不等式的性质2)
练习
若a>b>0>c,则下列不等式中成立的是(
).
(A)a+c(B)ab(C)
<
(D)
<
若a>b>0>c
(A)a+c(B)aba>b
b>c
a>0
若a>b>0>c,
(C)
<
(D)
<
a>c
b>0
a>b>0>c
<
a>b,a>0,b>0
0>c表示c为负数
a
b
已知a>b>0>c
方法一:
由已知
a>b,a>0,
所以
.
所以
,
因为0>c,即c为负数
<
所求
已知a>b>0>c
<
所求
方法二:
由已知
a>b,
所以
.
所以
,
因为0>c,即c为负数
又因为a>0,
方法三:
由已知
a>0,0>c,即c<0
,
所以
.
所以
,
由已知
a>b,
<
已知a>b>0>c
<
所求
练习
若a>b>0>c,则下列不等式中成立的是(
).
(A)a+c(B)ac>bc
(C)
>
(D)
<
D
不等式有哪些性质?不等式性质与等式性质的联系与区别是什么?
知识小结
在研究不等式性质的基本过程中运用了哪些数学思想方法?
类比
知识小结
分类讨论
从特殊到一般
人教版七年级下册教科书120页
习题9.1.
4.
设m>n,用“<”或“>”填空:
(1)m-5
n-5;
(2)m+4
n+4;
(3)6m
6n;
(4)
.
6.
设a>b,用“<”或“>”填空:
(1)2a-5
2b-5;
(2)-3.5b
+1
-3.5a
+1.
作业
同学们,再见!
初一年级
数学
不等式的性质(第一课时)
不等式
不等式的解
方程的解
等式
(方程)
等式的性质
不等式的性质
(不等式的解集)
不等式
不等式的解
方程的解
等式
(方程)
等式的性质
不等式的性质
(不等式的解集)
类比
等式有哪些性质?你能分别用文字语言和符号语言表示吗?
?
文字语言
符号语言
性质1
等式两边加(或减)同一个数(或式子),结果仍相等.
如果a=b,那么a+c=b+c,a-c=b-c.
性质2
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b,那么ac=bc.
如果a=b(c≠0),那么
.
等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
不等式两边加(或减)同一个数(或式子),大小关系会发生变化吗?
用“<”或“>”填空.
(1)5>3,
5+2
3+2,5+(-
)
3+(-
),5+0
3+0,
5-0.5
3-0.5,
5-(-4)
3-(-4);
>
>
>
>
>
<
<
<
<
(2)-1<3,
-1+0.5
3+0.5,
-1+(-2)
3+(-2),-1+0
3+0,
-1-
3-
,
-1-(-4)
3-(-4).
<
用“<”或“>”填空.
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
请同学再举一些例子,验证刚才的发现.
不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
那么a+c>b+c,a-c>b-c.
如果a>b,
符号语言:
不等式两边乘(或除以)同一个数,大小关系会改变吗?
请同学们自己举例,可以选取一些数字,计算一下.
6>2,
6×3
2×3,
6×(-0.5)
2×(-0.5),
6×0
2×0;
>
比如:
>
<
<
=
=
4>-2,
4×
-2×
,
4×(-5)
-2
×(-5)
,
4×0
-2×0
;
-3>-7,
-3×0.1
-7×0.1,
-3×(-2)
-7
×(-2),
-3×0
-7×0;
>
<
=
>
<
=
0<2,
0×4
2×4,
0×(-
)
2×(-
),
0×0
2×0.
不等式两边乘同一个正数,不等号的方向不变.
如果a>b,c>0,
那么ac>bc.
6>2,
6×3
>2×3;
-3>-7,
-3×0.5>-7×0.5;
0<2,
0×4<2×4.
4>-2,
4×
>-2×
;
不等式两边乘同一个负数,不等号的方向改变.
如果a>b,c<0,
那么ac
6×(-0.5)<2×(-0.5);
4>-2,
4×(-5)
<-2
×(-5)
;
-3>-7,
-3×(-2)<-7×(-2);
0<2,
0×(-
)
>2×(-
).
4>-2,
4×0=-2×0
;
6>2,6×0=2×0;
-3>-7,
-3×0=-7×0;
0<2,
0×0=2×0.
>
<
0不能作除数.
6>-2,
6÷
-2÷
6÷(-3)
-2÷(-3)
不等式性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变.
如果a>b,c>0,
那么ac>bc(或).
不等式性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果a>b,c<0,
那么ac
(或式子),不等号的方向不变.
不等式的性质2:不等式两边乘(或除以)同一个
正数,不等号的方向不变.
不等式的性质3:不等式两边乘(或除以)同一个
负数,不等号的方向改变.
例
设a>b,用“<”或“>”填空,并说明依据不等式的哪条性质:
(1)a-3
b-3;
(2)10a
10b;
(3)-9a
-9b;
(4)
;
(5)-3.5a+1
-3.5b+1.
(1)a-3
b-3
(
)
(2)10a
10b
(
)
(3)-9a
-9b
(
)
>
>
<
不等式的性质1
不等式的性质2
不等式的性质3
例
设a>b,用“<”或“>”填空,并说明依据不等式的哪条性质:
-3.5a
-3.5b
(
)
-3.5a+1<-3.5b+1
(不等式的性质1)
(4)
(
)
(5)-3.5a+1
-3.5b+1(
)
不等式的性质2
>
不等式的性质3
<
<
不等式的性质1、3
例
设a>b,用“<”或“>”填空,并说明依据不等式的哪条性质:
(1)
,两边都减去2,得
;(
)
(2)
,两边都加上–5,得
;(
)
不等式性质1
不等式性质1
不等式性质1
例
根据不等式的性质填空,并说明理由:
不等式性质1
不等式性质2
不等式性质3
例
根据不等式的性质填空,并说明理由:
(3)
,两边都除以
,得
;(
)
(4)
,两边都乘
,得
.
(
)
例
根据不等式的性质填空,并说明理由:
>
(1)如果m-5>n-5,那么m
n;
(2)如果-4a
>-4b
,那么a
b
;
<
(不等式的性质1)
(不等式的性质3)
(3)如果
,那么a
b
;
(4)如果
,那么a
b
.
<
>
(不等式的性质2)
(不等式的性质3)
例
根据不等式的性质填空,并说明理由:
<
<
<
>
>
-2a>-2b
练习
已知a
(1)
a+9
b+9
;
(2)-
a
-
b;
(3)
;
(4)3a-1.7
3b-1.7
;
(5)
.
3a<3b
>
(1)如果x+36>y+36,那么x
y;
(2)如果9a
>9b
,那么a
b
;
>
(不等式的性质1)
(不等式的性质2)
练习
根据不等式的性质填空,并说明理由:
练习
根据不等式的性质填空,并说明理由:
(3)如果
,那么m
n
;
(4)如果
,那么a
b
.
<
>
(不等式的性质3)
(不等式的性质2)
练习
若a>b>0>c,则下列不等式中成立的是(
).
(A)a+c
<
(D)
<
若a>b>0>c
(A)a+c
b>c
a>0
若a>b>0>c,
(C)
<
(D)
<
a>c
b>0
a>b>0>c
<
a>b,a>0,b>0
0>c表示c为负数
a
b
已知a>b>0>c
方法一:
由已知
a>b,a>0,
所以
.
所以
,
因为0>c,即c为负数
<
所求
已知a>b>0>c
<
所求
方法二:
由已知
a>b,
所以
.
所以
,
因为0>c,即c为负数
又因为a>0,
方法三:
由已知
a>0,0>c,即c<0
,
所以
.
所以
,
由已知
a>b,
<
已知a>b>0>c
<
所求
练习
若a>b>0>c,则下列不等式中成立的是(
).
(A)a+c
(C)
>
(D)
<
D
不等式有哪些性质?不等式性质与等式性质的联系与区别是什么?
知识小结
在研究不等式性质的基本过程中运用了哪些数学思想方法?
类比
知识小结
分类讨论
从特殊到一般
人教版七年级下册教科书120页
习题9.1.
4.
设m>n,用“<”或“>”填空:
(1)m-5
n-5;
(2)m+4
n+4;
(3)6m
6n;
(4)
.
6.
设a>b,用“<”或“>”填空:
(1)2a-5
2b-5;
(2)-3.5b
+1
-3.5a
+1.
作业
同学们,再见!
