人教版七年级下册数学7.2平面直角坐标系中的面积问题 课件(共16张PPT)
文档属性
| 名称 | 人教版七年级下册数学7.2平面直角坐标系中的面积问题 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 399.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-12 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
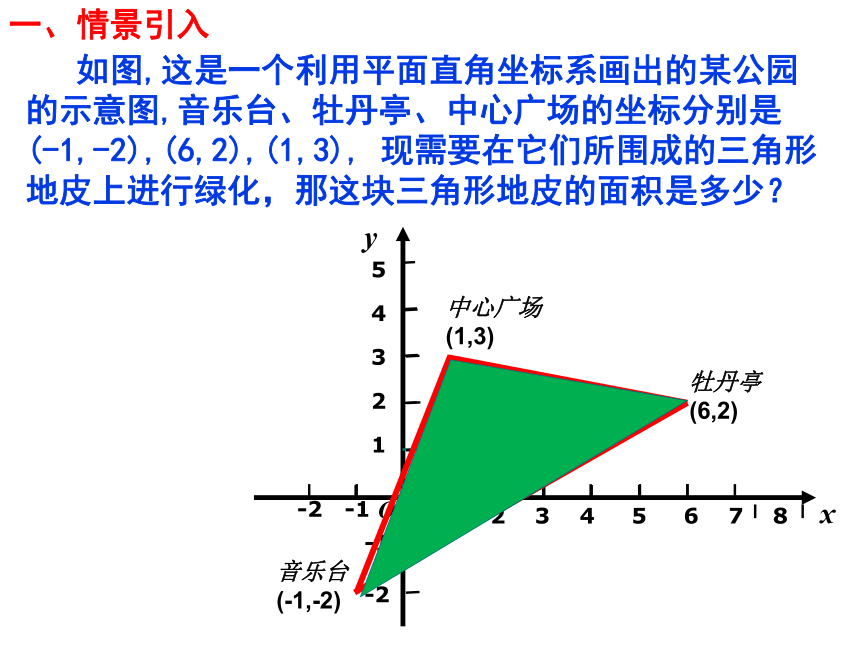
一、情景引入
如图,这是一个利用平面直角坐标系画出的某公园的示意图,音乐台、牡丹亭、中心广场的坐标分别是
(-1,-2),(6,2),(1,3),
现需要在它们所围成的三角形地皮上进行绿化,那这块三角形地皮的面积是多少?
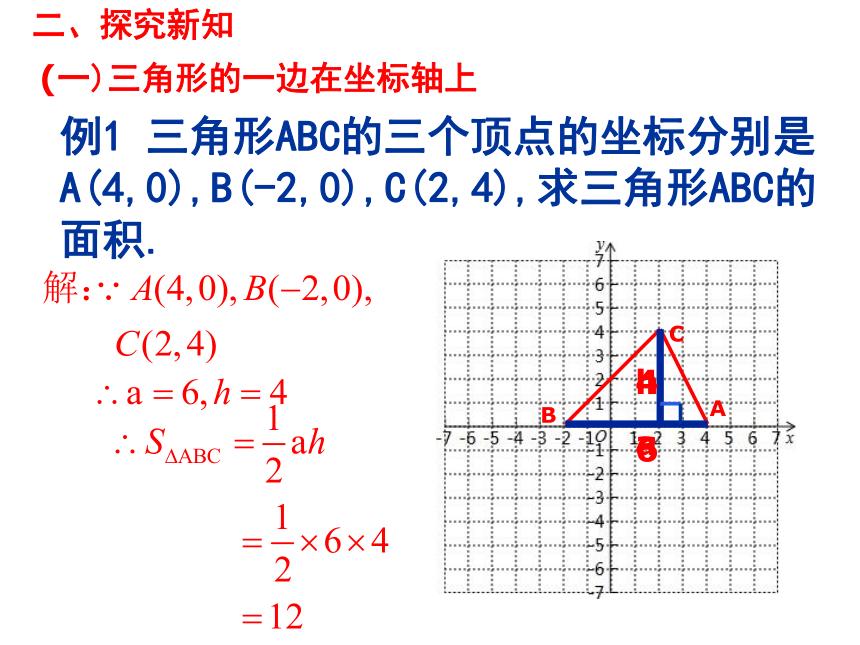
例1
三角形ABC的三个顶点的坐标分别是
A(4,0),B(-2,0),C(2,4),求三角形ABC的
面积.
(一)三角形的一边在坐标轴上
a
h
二、探究新知
4
6
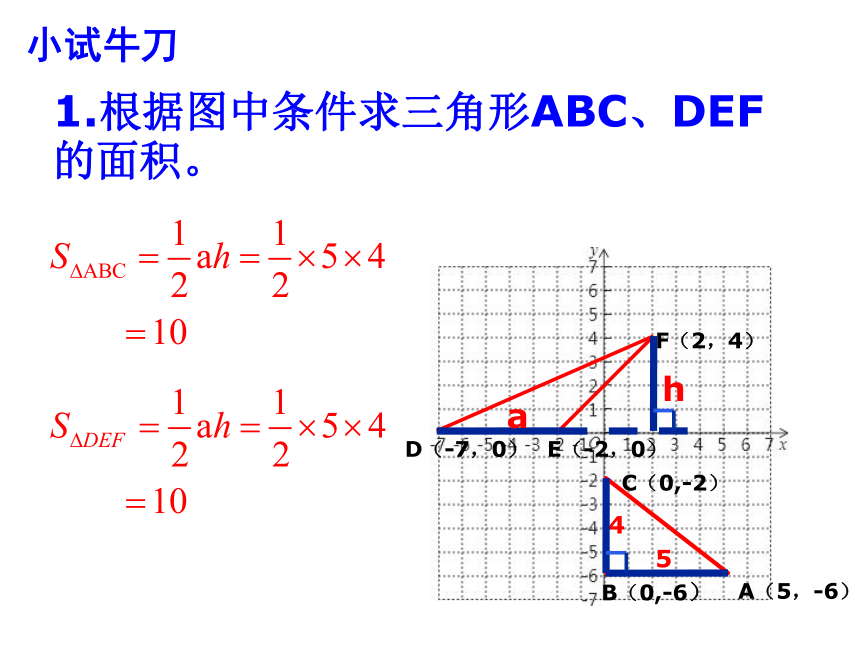
1.根据图中条件求三角形ABC、DEF
的面积。
5
4
F(2,4)
E(-2,0)
D(-7,0)
小试牛刀
a
h
3
4
(二)三角形的一边与坐标轴平行
C(-2,-5)
B(-5,-5)
A(-5,-1)
F(-5,2)
E(-5,6)
D(2,3)
2.根据图中条件求三角形ABC、DEF的面积。
7
4
小结归纳:
三角形的一边
在坐标轴上或
平行于坐标轴
以这条边为底,
再确定这条边
上的高
求三角形
的面积
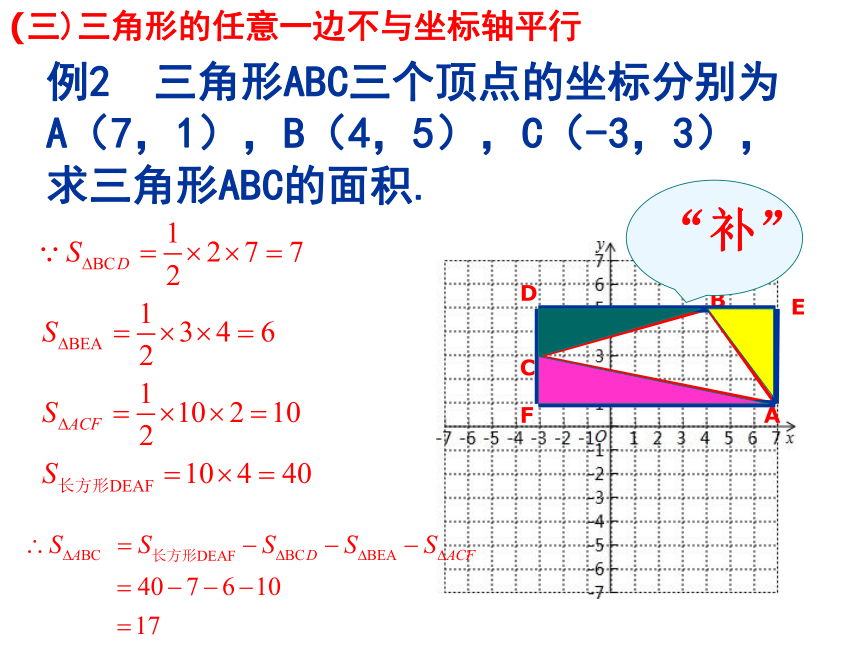
(三)三角形的任意一边不与坐标轴平行
例2
三角形ABC三个顶点的坐标分别为
A(7,1),B(4,5),C(-3,3),
求三角形ABC的面积.
D
F
E
“补”
例3
三角形ABC三个顶点的坐标分别为
A(7,1),B(4,5),C(-3,3),
求三角形ABC的面积.
(三)三角形的任意一边不与坐标轴平行
3.你能求情景引入中三角形地皮的面积吗?
解决问题
解决问题
3.你能求情景引入中三角形地皮的面积吗?
D
E
F
7
5
2
5
4
1
解:
4.
四边形ABCD四个顶点的坐标分别为
A(0,-2),B(3,0),C(7,-2),
D(4,-7)求四边形ABCD的面积.
D
拓展延伸
5.
四边形ABCD四个顶点的坐标分别为
A(-2,0),B(3,0),C(7,-2),
D(4,-7)求四边形ABCD的面积.
D
拓展延伸
“割”
小结归纳:
不能直接
求面积的
图形
可求面积
的图形
该图形的
面积
“补”
求差
“割”
求和
6.如图,
四边形ABOC的各个顶点的坐标分别是A(-5,4),B(-7,0),C(-2,5),O(0,0),求四边形ABCD的面积.
拓展应用
O
6.如图,
四边形ABOC的各个顶点的坐标分别是A(-5,4),B(-7,0),C(-2,5),O(0,0),求四边形ABCD的面积.
拓展应用
O
三、课堂总结:
平面直角坐标系中的面积问题:
1.可直接求面积的图形,关键是确定底和高。
2.若不能直接求面积的图形,可通过“割”
或“补”的方法,转化成易求面积的图形,利用几个图形面积的和或差求该图形的面积。
一、情景引入
如图,这是一个利用平面直角坐标系画出的某公园的示意图,音乐台、牡丹亭、中心广场的坐标分别是
(-1,-2),(6,2),(1,3),
现需要在它们所围成的三角形地皮上进行绿化,那这块三角形地皮的面积是多少?
例1
三角形ABC的三个顶点的坐标分别是
A(4,0),B(-2,0),C(2,4),求三角形ABC的
面积.
(一)三角形的一边在坐标轴上
a
h
二、探究新知
4
6
1.根据图中条件求三角形ABC、DEF
的面积。
5
4
F(2,4)
E(-2,0)
D(-7,0)
小试牛刀
a
h
3
4
(二)三角形的一边与坐标轴平行
C(-2,-5)
B(-5,-5)
A(-5,-1)
F(-5,2)
E(-5,6)
D(2,3)
2.根据图中条件求三角形ABC、DEF的面积。
7
4
小结归纳:
三角形的一边
在坐标轴上或
平行于坐标轴
以这条边为底,
再确定这条边
上的高
求三角形
的面积
(三)三角形的任意一边不与坐标轴平行
例2
三角形ABC三个顶点的坐标分别为
A(7,1),B(4,5),C(-3,3),
求三角形ABC的面积.
D
F
E
“补”
例3
三角形ABC三个顶点的坐标分别为
A(7,1),B(4,5),C(-3,3),
求三角形ABC的面积.
(三)三角形的任意一边不与坐标轴平行
3.你能求情景引入中三角形地皮的面积吗?
解决问题
解决问题
3.你能求情景引入中三角形地皮的面积吗?
D
E
F
7
5
2
5
4
1
解:
4.
四边形ABCD四个顶点的坐标分别为
A(0,-2),B(3,0),C(7,-2),
D(4,-7)求四边形ABCD的面积.
D
拓展延伸
5.
四边形ABCD四个顶点的坐标分别为
A(-2,0),B(3,0),C(7,-2),
D(4,-7)求四边形ABCD的面积.
D
拓展延伸
“割”
小结归纳:
不能直接
求面积的
图形
可求面积
的图形
该图形的
面积
“补”
求差
“割”
求和
6.如图,
四边形ABOC的各个顶点的坐标分别是A(-5,4),B(-7,0),C(-2,5),O(0,0),求四边形ABCD的面积.
拓展应用
O
6.如图,
四边形ABOC的各个顶点的坐标分别是A(-5,4),B(-7,0),C(-2,5),O(0,0),求四边形ABCD的面积.
拓展应用
O
三、课堂总结:
平面直角坐标系中的面积问题:
1.可直接求面积的图形,关键是确定底和高。
2.若不能直接求面积的图形,可通过“割”
或“补”的方法,转化成易求面积的图形,利用几个图形面积的和或差求该图形的面积。
