冀教版数学七年级下册7.5平行线的性质(一) 课件(共26张PPT)
文档属性
| 名称 | 冀教版数学七年级下册7.5平行线的性质(一) 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-15 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
7.5平行线的性质(一)
建筑数学
世界著名的
意大利比萨斜塔,
建于公元1173年,
为8层圆柱形建
筑,全部用白色
大理石砌成,塔
高54.5米。
1
2
目前,它与地面所成的较小的角为∠
1=85?。
它与地面所成的较大的角是多少度?
逆向思考
1.你学会了哪些判定两直线平行的方法?
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行。
2.现在我们逆向思考,把这些命题中的条件和结论互换,你能得出哪些命题?
两直线平行,
同位角相等;
两直线平行,
内错角相等;
两直线平行,同旁内角互补。
观察猜想
猜一猜:当a∥b时,∠1和∠2的大小有何关系?
b
1
2
a
c
心动
不如行动
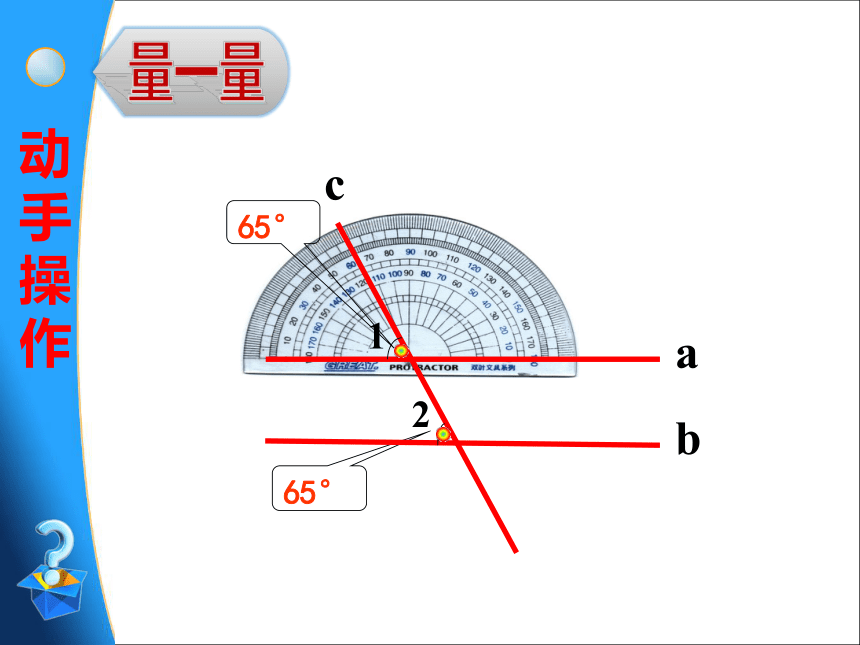
动手操作
65°
65°
c
a
b
1
2
量一量
b
2
a
c
1
拼一拼
动手操作
思考发现
想一想
通过刚才的观察猜想、动手操作、小组合作,你得出了什么结论?猜想与定理的区别是什么?
经过演绎推理证明正确的命题被称作定理,既然没有经过证明,那只能是猜想。此命题之所以被称为定理,是要说明的,在后续学习中,用反证法可以证明。
得出结论
平行线的性质定理1
两条平行线被第三条直线所截,同位角相等。
b
1
2
a
c
简称为:
几何语言:
∴∠1=∠2.
∵a∥b,
两直线平行,同位角相等。
实验探究
1.如图1,已知a∥b,找出图中所有的内错角、同旁内角,用自己的方法比较对应的内错角、同旁内角的数量关系。
图1
想一想
学会说理
2.如图2,直线AB∥CD,且被直线EF所截,
你能用已知的性质定理解释∠1=∠2吗?
图2
∵
AB∥CD
(已知)
想一想
∴
∠1=∠3
(两直线平行,
同位角相等)
∵
∠2=∠3
(对顶角相等)
∴
∠1=∠2
(等量代换)
得出结论
平行线的性质定理2
两条平行线被第三条直线所截,内错角相等。
简称为:
b
2
a
c
1
几何语言:
∴∠1=∠2.
∵a∥b,
两直线平行,内错角相等。
如图3,
学会说理
3.如图3,直线AB∥CD,且被直线EF所截,你
能用已知的性质定理解释∠1+∠2=180°吗?
图3
∵
AB∥CD
(已知)
还有其他方法吗?
想一想
∴
∠1=∠3
(
两直线平行,
同位角相等)
∵
∠2+∠3=180°(邻补角定义)
∴
∠1+∠2=180°(等量代换)
得出结论
平行线的性质定理3
两条平行线被第三条直线所截,同旁内角互补。
简称为:
2
b
1
a
c
几何语言:
∴∠1+∠2=180
°。
∵a∥b,
两直线平行,同旁内角互补。
1、如图直线a∥b
,∠1=70°,则∠2=_____
b
a
1
2
3
4
2、如图AB∥D
C,则______,理由是:_________;
AD∥BC,
则__________,理由:________。
(2题图)
(1题图)
A
B
C
D
2
1
基础练习(一)
70°
∠1=
∠3
∠2=
∠4
3、如图,若∠1=∠B,则___∥____,∠2+∠C=____
4、如图,梯形ABCD中,AD∥BC,
∠B=70°,∠D=135°
,
则∠A=____,∠C=____
A
D
B
C
(3题图)
(4题图)
A
B
C
D
E
1
2
基础练习(二)
DE
BC
180°
110°
45°
活动二:
对比分析
平行线的判定和性质有什么联系和区别?
?
条件
结论
判定
同位角相等
两直线平行
内错角相等
同旁内角互补
性质
两直线平行
同位角相等
内错角相等
同旁内角互补
想一想
抢答:如图已知直线a、b被直线c所截,在括号内为下面的推理填上适当的根据:
(1)∵
a∥b,∴∠3=∠1(
)
(2)∵
∠3=∠1,∴
a∥b
(
)
(3)
∵
a∥b,∴∠2=∠1(
)
(4)
∵
a∥b,
∴∠1
+
∠
4=
180°(
)
(5)
∵
∠1=∠2,∴
a∥b
(
)
(6)∠1
+
∠
4=
180
°
∴
a∥b
(
)
c
1
b
a
2
3
4
1.两条直线被第三条直线所截,则
(
)
A.同位角相等
B.内错角互补
C.同旁内角相等
D.以上结论都不对
2.
两条平行线被第三条直线所截得的角中角平分线互相垂直的是
(
)
A.内错角
B.同位角
C.同旁内角
D.以上结论都不对
D
A
有理有据
已知:如图4,a∥b,c∥d,
∠1=73°。
求
∠2和∠3的度数。
图4
解:∵
a∥b
(已知),
∴
∠1=∠2
(两直线平行,
内错角相等)。
∵
∠1=73°(已知),
∴
∠2=73°(等量代换)。
∵
c∥d
(已知),
∴
∠2+∠3=180°
(两直线平行,
同旁内角互补)。
∴
∠3=180°—∠2
(等式的性质)。
∴
∠3=180°—73°=107°(等量代换)。
有理有据
1.如图5,已知AB∥CD,∠1=110°,求∠2、∠3、∠4的度数。
图5
2.下面写出了命题“如图6,如果∠B=∠C,
那么∠A+∠1=180°”的说理过程,请你填空:
∵
∠B=∠C
(
),
∴
∥
(
).
∴∠A+∠1=180°
(
).
图6
建筑数学
1
3
2
目前,它与地面所成的较小的角为∠
1=85?。
它与地面所成的较大的角是多少度?
解决问题
1.如图,要设计一个弯形管道ABCD,且管道AB∥CD,
∠ABC=120°,那么如何设计∠BCD的角度呢?
第1题
2.如图,一条公路两次拐弯后,和原来的方向相
同,也就是拐弯前后的两条路互相平行。如果
∠
B等于142°,那么
∠
C是多少度?为什么?
B
C
第2题
用一用
3、如图,AB∥EF,
CD∥EF
,∠B=40°、∠D=35
°,
求∠BED的大小。
A
B
F
D
E
C
提高练习
类比
由角的大小关系转化为直线的位置关系
平行线的
判定
平行线的
性质
由直线的位置关系转化为角的大小关系
转化的数学思想
知识与方法
1.我们学到了哪些知识?
两直线平行,
同位角相等;
两直线平行,
内错角相等;
两直线平行,同旁内角互补。
2.
平行线的性质与判定的联系和区别:
判定
同旁内角互补
内错角相等
同位角相等
两直线平行
性质
同学们再见!
7.5平行线的性质(一)
建筑数学
世界著名的
意大利比萨斜塔,
建于公元1173年,
为8层圆柱形建
筑,全部用白色
大理石砌成,塔
高54.5米。
1
2
目前,它与地面所成的较小的角为∠
1=85?。
它与地面所成的较大的角是多少度?
逆向思考
1.你学会了哪些判定两直线平行的方法?
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行。
2.现在我们逆向思考,把这些命题中的条件和结论互换,你能得出哪些命题?
两直线平行,
同位角相等;
两直线平行,
内错角相等;
两直线平行,同旁内角互补。
观察猜想
猜一猜:当a∥b时,∠1和∠2的大小有何关系?
b
1
2
a
c
心动
不如行动
动手操作
65°
65°
c
a
b
1
2
量一量
b
2
a
c
1
拼一拼
动手操作
思考发现
想一想
通过刚才的观察猜想、动手操作、小组合作,你得出了什么结论?猜想与定理的区别是什么?
经过演绎推理证明正确的命题被称作定理,既然没有经过证明,那只能是猜想。此命题之所以被称为定理,是要说明的,在后续学习中,用反证法可以证明。
得出结论
平行线的性质定理1
两条平行线被第三条直线所截,同位角相等。
b
1
2
a
c
简称为:
几何语言:
∴∠1=∠2.
∵a∥b,
两直线平行,同位角相等。
实验探究
1.如图1,已知a∥b,找出图中所有的内错角、同旁内角,用自己的方法比较对应的内错角、同旁内角的数量关系。
图1
想一想
学会说理
2.如图2,直线AB∥CD,且被直线EF所截,
你能用已知的性质定理解释∠1=∠2吗?
图2
∵
AB∥CD
(已知)
想一想
∴
∠1=∠3
(两直线平行,
同位角相等)
∵
∠2=∠3
(对顶角相等)
∴
∠1=∠2
(等量代换)
得出结论
平行线的性质定理2
两条平行线被第三条直线所截,内错角相等。
简称为:
b
2
a
c
1
几何语言:
∴∠1=∠2.
∵a∥b,
两直线平行,内错角相等。
如图3,
学会说理
3.如图3,直线AB∥CD,且被直线EF所截,你
能用已知的性质定理解释∠1+∠2=180°吗?
图3
∵
AB∥CD
(已知)
还有其他方法吗?
想一想
∴
∠1=∠3
(
两直线平行,
同位角相等)
∵
∠2+∠3=180°(邻补角定义)
∴
∠1+∠2=180°(等量代换)
得出结论
平行线的性质定理3
两条平行线被第三条直线所截,同旁内角互补。
简称为:
2
b
1
a
c
几何语言:
∴∠1+∠2=180
°。
∵a∥b,
两直线平行,同旁内角互补。
1、如图直线a∥b
,∠1=70°,则∠2=_____
b
a
1
2
3
4
2、如图AB∥D
C,则______,理由是:_________;
AD∥BC,
则__________,理由:________。
(2题图)
(1题图)
A
B
C
D
2
1
基础练习(一)
70°
∠1=
∠3
∠2=
∠4
3、如图,若∠1=∠B,则___∥____,∠2+∠C=____
4、如图,梯形ABCD中,AD∥BC,
∠B=70°,∠D=135°
,
则∠A=____,∠C=____
A
D
B
C
(3题图)
(4题图)
A
B
C
D
E
1
2
基础练习(二)
DE
BC
180°
110°
45°
活动二:
对比分析
平行线的判定和性质有什么联系和区别?
?
条件
结论
判定
同位角相等
两直线平行
内错角相等
同旁内角互补
性质
两直线平行
同位角相等
内错角相等
同旁内角互补
想一想
抢答:如图已知直线a、b被直线c所截,在括号内为下面的推理填上适当的根据:
(1)∵
a∥b,∴∠3=∠1(
)
(2)∵
∠3=∠1,∴
a∥b
(
)
(3)
∵
a∥b,∴∠2=∠1(
)
(4)
∵
a∥b,
∴∠1
+
∠
4=
180°(
)
(5)
∵
∠1=∠2,∴
a∥b
(
)
(6)∠1
+
∠
4=
180
°
∴
a∥b
(
)
c
1
b
a
2
3
4
1.两条直线被第三条直线所截,则
(
)
A.同位角相等
B.内错角互补
C.同旁内角相等
D.以上结论都不对
2.
两条平行线被第三条直线所截得的角中角平分线互相垂直的是
(
)
A.内错角
B.同位角
C.同旁内角
D.以上结论都不对
D
A
有理有据
已知:如图4,a∥b,c∥d,
∠1=73°。
求
∠2和∠3的度数。
图4
解:∵
a∥b
(已知),
∴
∠1=∠2
(两直线平行,
内错角相等)。
∵
∠1=73°(已知),
∴
∠2=73°(等量代换)。
∵
c∥d
(已知),
∴
∠2+∠3=180°
(两直线平行,
同旁内角互补)。
∴
∠3=180°—∠2
(等式的性质)。
∴
∠3=180°—73°=107°(等量代换)。
有理有据
1.如图5,已知AB∥CD,∠1=110°,求∠2、∠3、∠4的度数。
图5
2.下面写出了命题“如图6,如果∠B=∠C,
那么∠A+∠1=180°”的说理过程,请你填空:
∵
∠B=∠C
(
),
∴
∥
(
).
∴∠A+∠1=180°
(
).
图6
建筑数学
1
3
2
目前,它与地面所成的较小的角为∠
1=85?。
它与地面所成的较大的角是多少度?
解决问题
1.如图,要设计一个弯形管道ABCD,且管道AB∥CD,
∠ABC=120°,那么如何设计∠BCD的角度呢?
第1题
2.如图,一条公路两次拐弯后,和原来的方向相
同,也就是拐弯前后的两条路互相平行。如果
∠
B等于142°,那么
∠
C是多少度?为什么?
B
C
第2题
用一用
3、如图,AB∥EF,
CD∥EF
,∠B=40°、∠D=35
°,
求∠BED的大小。
A
B
F
D
E
C
提高练习
类比
由角的大小关系转化为直线的位置关系
平行线的
判定
平行线的
性质
由直线的位置关系转化为角的大小关系
转化的数学思想
知识与方法
1.我们学到了哪些知识?
两直线平行,
同位角相等;
两直线平行,
内错角相等;
两直线平行,同旁内角互补。
2.
平行线的性质与判定的联系和区别:
判定
同旁内角互补
内错角相等
同位角相等
两直线平行
性质
同学们再见!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
