第05节 自然界中的守恒定律 :16张PPT
文档属性
| 名称 | 第05节 自然界中的守恒定律 :16张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-14 05:03:51 | ||
图片预览






文档简介
(共16张PPT)
《自然界中的守恒定律》的应用
-------“弹簧模型”
1、能量守恒:
机械能守恒的条件:
2、动量守恒:
动量守恒的条件:
复习:
系统内,只有重力或弹簧弹力做功
(1)严格守恒:系统不受外力作用,或系统所受合外力为零.
(2)近似守恒:系统受外力作用,但当系统所受的外力远小于系统内各物体间的内力时,系统的总动量近似守恒.
(3)某方向上守恒:系统受外力作用,所受的合外力不为零,但在某一方向上合外力为零,则系统在该方向上动量守恒.
“一动碰一静”模型:(水平地面光滑)
m1
m2
3、物体发生弹性碰撞,
m1v0=m1v1+m2v2
①
①若m1=m2,
②若m1>m2,
③若m1则v′1=0,v′2=v1,
碰后两球速度发生变换.
则v1′>0和v2′>0,
碰后v1′和v2′都与v1方向相同.
则v1′<0,碰后v1′与v1方向相反,
即m1被弹回.
1.(动量守恒条件的理解)(多选)如图所示,在光滑水平地面上有A、B两个木块,A、B之间用一轻弹簧连接.A靠在墙壁上,用力F向左推B使两木块之间的弹簧压缩并处于静止状态.若突然撤去力F,则下列说法中正确的是( )
A.木块A离开墙壁前,A、B和弹簧组成的系统动量守恒,机械能也守恒
B.木块A离开墙壁前,A、B和弹簧组成的系统动量不守恒,但机械能守恒
C.木块A离开墙壁后,A、B和弹簧组成的系统动量守恒,机械能也守恒
D.木块A离开墙壁后,A、B和弹簧组成的系统动量不守恒,但机械能守恒
课前练习:
BC
2.
(动量守恒条件的理解)一颗子弹水平射入置于光滑水平面上的木块A并留在其中,A、B用一根弹性良好的轻质弹簧连在一起,如图所示.则在子弹打击木块A及弹簧被压缩的过程中,对子弹、两木块和弹簧组成的系统(
)
A.动量守恒,机械能守恒
B.动量不守恒,机械能守恒
C.动量守恒,机械能不守恒
D.无法判定动量、机械能是否守恒
C
3、如图所示,置于光滑水平面上,B与一轻质弹簧的一端相
连,木块B的质量为2
kg,弹簧的另一端固定在竖直挡板上,当B以4
m/s的速度压缩弹簧,当弹簧被压缩到最短时,弹簧具有的弹性势能大小为(
)
A.4
J
B.8
J
C.16
J
D.32
J
C
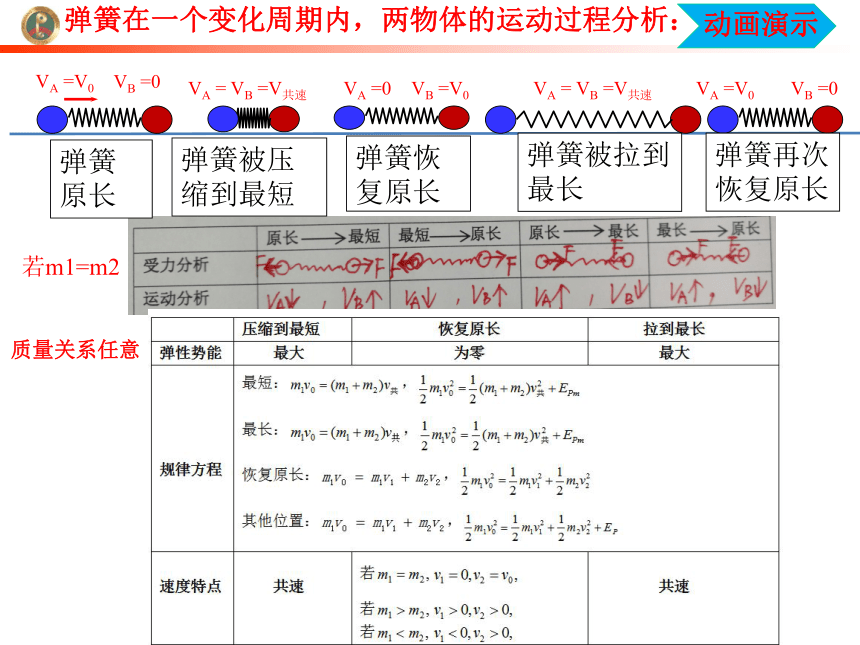
弹簧在一个变化周期内,两物体的运动过程分析:
VA
=V0
VB
=0
弹簧原长
弹簧被压缩到最短
弹簧恢复原长
弹簧被拉到最长
弹簧再次恢复原长
动画演示
若m1=m2
质量关系任意
VA
=
VB
=V共速
VA
=V0
VB
=0
VA
=
VB
=V共速
VB
=V0
弹簧在一个变化周期内,两物体的运动过程分析:
VA
=0
VA
=V0
VB
=0
弹簧原长
弹簧被压缩到最短
弹簧恢复原长
弹簧被拉到最长
弹簧再次恢复原长
动画演示
若m1=m2
质量关系任意
基础任务1:弹簧被压缩到最短时的弹性势能等于( )
A.4
J
B.8
J
C.16
J
D.32
J
基础任务2:弹簧再次恢复原长时,P、Q两物体的速度分别是(
)
A.
4
m/s,
0
B.
2
m/s,
2
m/s,
C.
1
m/s,
3
m/s,
D.
0
,
4
m/s
基础任务3:当物体P的速度为1
m/s时,弹簧的弹性势能是(
)
A.4
J
B.6
J
C.8
J
D.16
J
D
B
例题1:如图所示,位于光滑水平桌面上的小滑块P和Q质量均为2
kg,都可视为质点.Q与轻质弹簧相连。设Q
静止,P以4
m/s的初速度向Q运动并与弹簧发生碰撞,P与弹簧接触后不再与弹簧分开。
(做完可以到“微课中心”观看微课)
B
一、两物体与弹簧系统的运动过程分析
完成基本任务后可以继续完成以下拓展任务(可以到“微课中心”观看微课):
拓展任务1:如图所示,位于光滑水平桌面上的小滑块P和Q质量分别为4
kg、2
kg,,都可视为质点.Q与轻质弹簧相连。设Q静止,P以4
m/s的初速度向Q运动并与弹簧发生碰撞,
P与弹簧接触后不再与弹簧分开。弹簧再次恢复原长时,P、Q两物体的速度分别是(
)
B
完成基本任务后可以继续完成以下拓展任务(可以到“微课中心”观看微课):
拓展任务2:如图所示,位于光滑水平桌面上的小滑块P和Q质量分别为
2kg、4
kg,,都可视为质点.Q与轻质弹簧相连。设Q静止,P以4
m/s的初速度向Q运动并与弹簧发生碰撞,
P与弹簧接触后不再与弹簧分开。弹簧再次恢复原长时,P、Q两物体的速度分别是(
)
小结:两物体夹着弹簧在运动过程中,满足:
1、动量守恒
2、机械能守恒(能量守恒)。
D
视频演示
二、三个物体与弹簧组成的系统
例题2、如图所示,一轻质弹簧两端连着物体A和B,放在光滑的水平面上,物体A被水平速度为v0的子弹射中并且子弹嵌在其中.已知子弹的质量为m,物体A的质量为3m,物体B的质量为4m,
基础任务1:弹簧压缩到最短时B的速度大小为(
)
基础任务2:系统中弹簧的最大弹性势能(
)
C
A
例题2、如图所示,一轻质弹簧两端连着物体A和B,放在光滑的水平面上,物体A被水平速度为v0的子弹射中并且子弹嵌在其中.已知子弹的质量为m,物体A的质量为3m,物体B的质量为4m,
基础任务1:弹簧压缩到最短时B的速度大小为(
)
解析:弹簧压缩到最短时,子弹、物体A、B具有共同的速度v1,且子弹、物体A、物体B组成的系统,从子弹开始射入物体A一直到弹簧被压缩到最短的过程中,整个过程系统的动量守恒,
由动量守恒定律得mv0=(m+mA+mB)v1,故v1=v0/8
C
例题2、如图所示,一轻质弹簧两端连着物体A和B,放在光滑的水平面上,物体A被水平速度为v0的子弹射中并且子弹嵌在其中.已知子弹的质量为m,物体A的质量为3m,物体B的质量为4m,
基础任务2:系统中弹簧的最大弹性势能(
)
A
拓展任务3:两物块A、B用轻弹簧相连,质量均为2
kg,初始时弹簧处于原长,A、B两物块都以v=6
m/s的速度在光滑的水平地面上运动,质量为4
kg的物块C静止在前方,如图3所示.B与C碰撞后二者会粘在一起运动.则在以后的运动中:
(1)当弹簧的弹性势能最大时,物块A的速度为多大?
(2)系统中弹性势能的最大值是多少?
处理弹簧模型问题的步骤:
1、受力分析、过程分析。
2、利用动量守恒定律列方程:
选系统、选过程、判条件。
3、利用能量守恒定律列方程。
注意:若过程中发生非弹性碰撞,则机械能不守恒,但总能量守恒。
《自然界中的守恒定律》的应用
-------“弹簧模型”
1、能量守恒:
机械能守恒的条件:
2、动量守恒:
动量守恒的条件:
复习:
系统内,只有重力或弹簧弹力做功
(1)严格守恒:系统不受外力作用,或系统所受合外力为零.
(2)近似守恒:系统受外力作用,但当系统所受的外力远小于系统内各物体间的内力时,系统的总动量近似守恒.
(3)某方向上守恒:系统受外力作用,所受的合外力不为零,但在某一方向上合外力为零,则系统在该方向上动量守恒.
“一动碰一静”模型:(水平地面光滑)
m1
m2
3、物体发生弹性碰撞,
m1v0=m1v1+m2v2
①
①若m1=m2,
②若m1>m2,
③若m1
碰后两球速度发生变换.
则v1′>0和v2′>0,
碰后v1′和v2′都与v1方向相同.
则v1′<0,碰后v1′与v1方向相反,
即m1被弹回.
1.(动量守恒条件的理解)(多选)如图所示,在光滑水平地面上有A、B两个木块,A、B之间用一轻弹簧连接.A靠在墙壁上,用力F向左推B使两木块之间的弹簧压缩并处于静止状态.若突然撤去力F,则下列说法中正确的是( )
A.木块A离开墙壁前,A、B和弹簧组成的系统动量守恒,机械能也守恒
B.木块A离开墙壁前,A、B和弹簧组成的系统动量不守恒,但机械能守恒
C.木块A离开墙壁后,A、B和弹簧组成的系统动量守恒,机械能也守恒
D.木块A离开墙壁后,A、B和弹簧组成的系统动量不守恒,但机械能守恒
课前练习:
BC
2.
(动量守恒条件的理解)一颗子弹水平射入置于光滑水平面上的木块A并留在其中,A、B用一根弹性良好的轻质弹簧连在一起,如图所示.则在子弹打击木块A及弹簧被压缩的过程中,对子弹、两木块和弹簧组成的系统(
)
A.动量守恒,机械能守恒
B.动量不守恒,机械能守恒
C.动量守恒,机械能不守恒
D.无法判定动量、机械能是否守恒
C
3、如图所示,置于光滑水平面上,B与一轻质弹簧的一端相
连,木块B的质量为2
kg,弹簧的另一端固定在竖直挡板上,当B以4
m/s的速度压缩弹簧,当弹簧被压缩到最短时,弹簧具有的弹性势能大小为(
)
A.4
J
B.8
J
C.16
J
D.32
J
C
弹簧在一个变化周期内,两物体的运动过程分析:
VA
=V0
VB
=0
弹簧原长
弹簧被压缩到最短
弹簧恢复原长
弹簧被拉到最长
弹簧再次恢复原长
动画演示
若m1=m2
质量关系任意
VA
=
VB
=V共速
VA
=V0
VB
=0
VA
=
VB
=V共速
VB
=V0
弹簧在一个变化周期内,两物体的运动过程分析:
VA
=0
VA
=V0
VB
=0
弹簧原长
弹簧被压缩到最短
弹簧恢复原长
弹簧被拉到最长
弹簧再次恢复原长
动画演示
若m1=m2
质量关系任意
基础任务1:弹簧被压缩到最短时的弹性势能等于( )
A.4
J
B.8
J
C.16
J
D.32
J
基础任务2:弹簧再次恢复原长时,P、Q两物体的速度分别是(
)
A.
4
m/s,
0
B.
2
m/s,
2
m/s,
C.
1
m/s,
3
m/s,
D.
0
,
4
m/s
基础任务3:当物体P的速度为1
m/s时,弹簧的弹性势能是(
)
A.4
J
B.6
J
C.8
J
D.16
J
D
B
例题1:如图所示,位于光滑水平桌面上的小滑块P和Q质量均为2
kg,都可视为质点.Q与轻质弹簧相连。设Q
静止,P以4
m/s的初速度向Q运动并与弹簧发生碰撞,P与弹簧接触后不再与弹簧分开。
(做完可以到“微课中心”观看微课)
B
一、两物体与弹簧系统的运动过程分析
完成基本任务后可以继续完成以下拓展任务(可以到“微课中心”观看微课):
拓展任务1:如图所示,位于光滑水平桌面上的小滑块P和Q质量分别为4
kg、2
kg,,都可视为质点.Q与轻质弹簧相连。设Q静止,P以4
m/s的初速度向Q运动并与弹簧发生碰撞,
P与弹簧接触后不再与弹簧分开。弹簧再次恢复原长时,P、Q两物体的速度分别是(
)
B
完成基本任务后可以继续完成以下拓展任务(可以到“微课中心”观看微课):
拓展任务2:如图所示,位于光滑水平桌面上的小滑块P和Q质量分别为
2kg、4
kg,,都可视为质点.Q与轻质弹簧相连。设Q静止,P以4
m/s的初速度向Q运动并与弹簧发生碰撞,
P与弹簧接触后不再与弹簧分开。弹簧再次恢复原长时,P、Q两物体的速度分别是(
)
小结:两物体夹着弹簧在运动过程中,满足:
1、动量守恒
2、机械能守恒(能量守恒)。
D
视频演示
二、三个物体与弹簧组成的系统
例题2、如图所示,一轻质弹簧两端连着物体A和B,放在光滑的水平面上,物体A被水平速度为v0的子弹射中并且子弹嵌在其中.已知子弹的质量为m,物体A的质量为3m,物体B的质量为4m,
基础任务1:弹簧压缩到最短时B的速度大小为(
)
基础任务2:系统中弹簧的最大弹性势能(
)
C
A
例题2、如图所示,一轻质弹簧两端连着物体A和B,放在光滑的水平面上,物体A被水平速度为v0的子弹射中并且子弹嵌在其中.已知子弹的质量为m,物体A的质量为3m,物体B的质量为4m,
基础任务1:弹簧压缩到最短时B的速度大小为(
)
解析:弹簧压缩到最短时,子弹、物体A、B具有共同的速度v1,且子弹、物体A、物体B组成的系统,从子弹开始射入物体A一直到弹簧被压缩到最短的过程中,整个过程系统的动量守恒,
由动量守恒定律得mv0=(m+mA+mB)v1,故v1=v0/8
C
例题2、如图所示,一轻质弹簧两端连着物体A和B,放在光滑的水平面上,物体A被水平速度为v0的子弹射中并且子弹嵌在其中.已知子弹的质量为m,物体A的质量为3m,物体B的质量为4m,
基础任务2:系统中弹簧的最大弹性势能(
)
A
拓展任务3:两物块A、B用轻弹簧相连,质量均为2
kg,初始时弹簧处于原长,A、B两物块都以v=6
m/s的速度在光滑的水平地面上运动,质量为4
kg的物块C静止在前方,如图3所示.B与C碰撞后二者会粘在一起运动.则在以后的运动中:
(1)当弹簧的弹性势能最大时,物块A的速度为多大?
(2)系统中弹性势能的最大值是多少?
处理弹簧模型问题的步骤:
1、受力分析、过程分析。
2、利用动量守恒定律列方程:
选系统、选过程、判条件。
3、利用能量守恒定律列方程。
注意:若过程中发生非弹性碰撞,则机械能不守恒,但总能量守恒。
同课章节目录
