粤教版高中物理选修3-5第一章第02节 动量 动量守恒定律(共15张PPT)
文档属性
| 名称 | 粤教版高中物理选修3-5第一章第02节 动量 动量守恒定律(共15张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-14 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
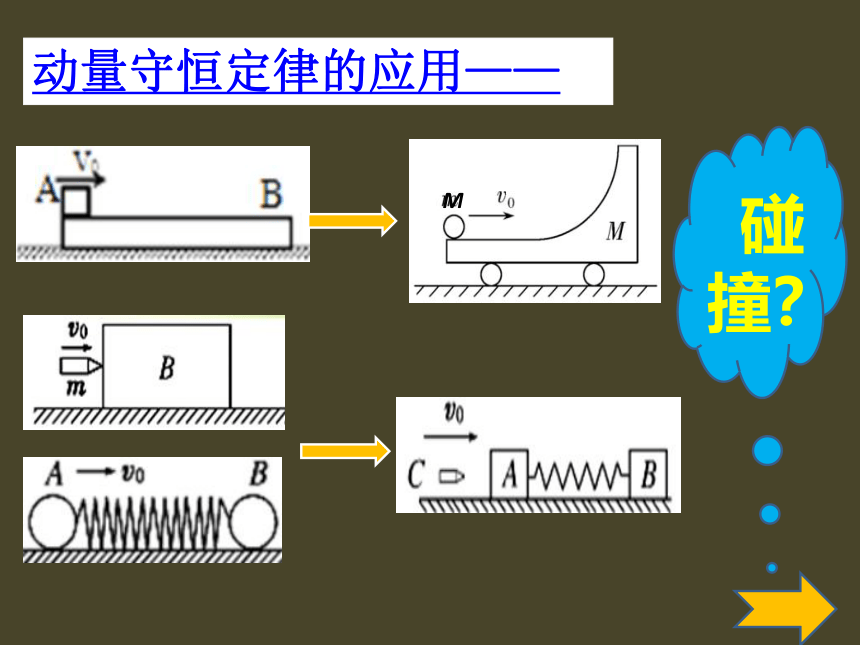
动量守恒定律的应用——
《碰撞的分类及拓展》
动量守恒定律的应用——
一、碰撞的特点
1.
碰撞时间极短,可忽略不计.
2.
碰撞过程中内力远大于外力,系统
所受外力可忽略不计,故系统的动
量守恒.
3.
碰撞后动能不增加,即Ek≥Ek′
1.
弹性碰撞
①动量守恒:m1v1+m2v2=m1v1′+m2v2′
②动能守恒:
③特例:当满足弹性碰撞且质量m1=
m2时,物体速度互换
,即:
二、碰撞的分类
二、碰撞的分类
2.
非弹性碰撞
①动量守恒:m1v1+m2v2=m1v1′+m2v2′
②动能损失:损失的动能转化为其他形式
的能。
③特例:完全非弹性碰撞---碰后共速
动量守恒:m1v1+m2v2=(m1+m2)
v共
动能损失最多
三、碰撞问题的拓展
1.
类碰撞模型之“滑块+木板”
【思考一】:是否存在类似弹性
碰撞或非弹性碰撞的子过程?
【思考二】:小球将从何处离开小
车,
离开小车后将做什么运动?
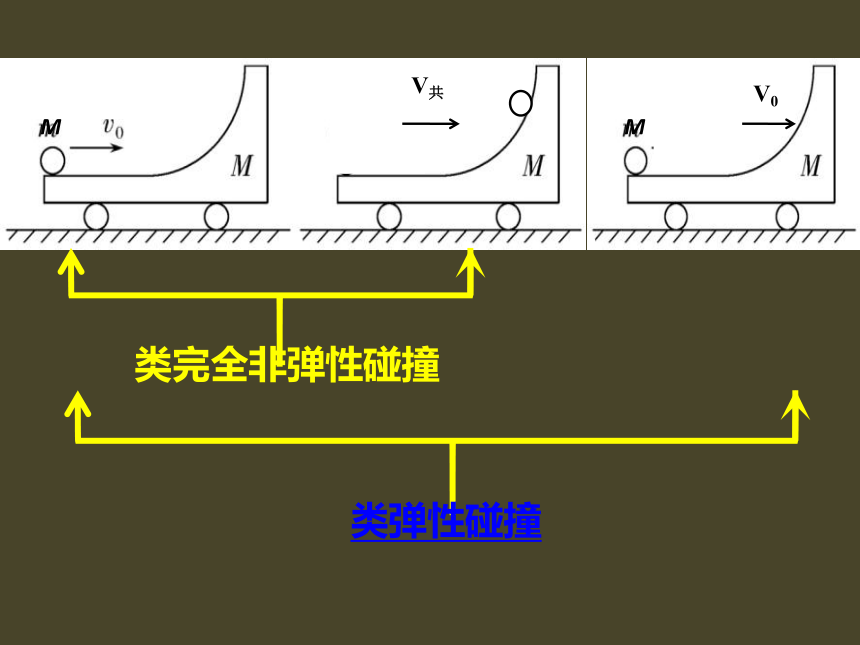
类完全非弹性碰撞
类弹性碰撞
类完全非弹性碰撞
类弹性碰撞
三、碰撞问题的拓展
2.
类碰撞模型之“滑块+弹簧+滑块”
【思考一】:是否存在类弹性碰撞或完全非弹性碰撞的子过程?
【思考二】:当弹簧出于什么状态时,木块A有最小速度?且满足什么条件时,木块A速度能反向?
【例】如图所示,光滑水平面上有一处于原长的弹簧,两端分别和物块A
、B连接。已知A、
B的质量为mA和mB,现给物块A一水平向左的瞬时速度V0,试讨论在以后的运动过程中
V0
V0
V共
V1
V2
类完全非弹性碰撞
V共
类弹性碰撞
A,B共速
弹簧压缩
到最短
弹簧恢复
到原长
A,B共速
弹簧拉伸
到最长
初态弹簧原长
初态弹簧原长
四、规律总结
处理碰撞或类碰撞问题时,选择不同的末状态,通过对相应过程的能量分析,可类比为弹性或完全非弹性碰撞,运用动量守恒和能量关系来求解。
类完全非弹性碰撞问题
(1)共性---动量守恒,动能损失最大,末状态共速。
(2)个性---因做功情况不同,损失的动能转化为其他形式能的情况不同
四、课后探究
思考2:如何运用已学知识论证课前
的实验现象的规律。
思考1:如何运用已学知识,分析类碰
撞之“子弹打木块”模型。
【拓展】一轻质弹簧的两端连接两滑块
A和B,已知mA、mB,放在光滑水平面上,
开始时弹簧处于原长,现滑块A被水平
飞来的质量为mC,速度为v0的子弹击中,
且没有穿出,如图所示,求:以后运动
过程中弹簧的最大弹性势能。
把简单的事情做彻底,把平凡的事情做经典,把每一件小事都做得更精彩。
谢
谢
指
导
动量守恒定律的应用——
《碰撞的分类及拓展》
动量守恒定律的应用——
一、碰撞的特点
1.
碰撞时间极短,可忽略不计.
2.
碰撞过程中内力远大于外力,系统
所受外力可忽略不计,故系统的动
量守恒.
3.
碰撞后动能不增加,即Ek≥Ek′
1.
弹性碰撞
①动量守恒:m1v1+m2v2=m1v1′+m2v2′
②动能守恒:
③特例:当满足弹性碰撞且质量m1=
m2时,物体速度互换
,即:
二、碰撞的分类
二、碰撞的分类
2.
非弹性碰撞
①动量守恒:m1v1+m2v2=m1v1′+m2v2′
②动能损失:损失的动能转化为其他形式
的能。
③特例:完全非弹性碰撞---碰后共速
动量守恒:m1v1+m2v2=(m1+m2)
v共
动能损失最多
三、碰撞问题的拓展
1.
类碰撞模型之“滑块+木板”
【思考一】:是否存在类似弹性
碰撞或非弹性碰撞的子过程?
【思考二】:小球将从何处离开小
车,
离开小车后将做什么运动?
类完全非弹性碰撞
类弹性碰撞
类完全非弹性碰撞
类弹性碰撞
三、碰撞问题的拓展
2.
类碰撞模型之“滑块+弹簧+滑块”
【思考一】:是否存在类弹性碰撞或完全非弹性碰撞的子过程?
【思考二】:当弹簧出于什么状态时,木块A有最小速度?且满足什么条件时,木块A速度能反向?
【例】如图所示,光滑水平面上有一处于原长的弹簧,两端分别和物块A
、B连接。已知A、
B的质量为mA和mB,现给物块A一水平向左的瞬时速度V0,试讨论在以后的运动过程中
V0
V0
V共
V1
V2
类完全非弹性碰撞
V共
类弹性碰撞
A,B共速
弹簧压缩
到最短
弹簧恢复
到原长
A,B共速
弹簧拉伸
到最长
初态弹簧原长
初态弹簧原长
四、规律总结
处理碰撞或类碰撞问题时,选择不同的末状态,通过对相应过程的能量分析,可类比为弹性或完全非弹性碰撞,运用动量守恒和能量关系来求解。
类完全非弹性碰撞问题
(1)共性---动量守恒,动能损失最大,末状态共速。
(2)个性---因做功情况不同,损失的动能转化为其他形式能的情况不同
四、课后探究
思考2:如何运用已学知识论证课前
的实验现象的规律。
思考1:如何运用已学知识,分析类碰
撞之“子弹打木块”模型。
【拓展】一轻质弹簧的两端连接两滑块
A和B,已知mA、mB,放在光滑水平面上,
开始时弹簧处于原长,现滑块A被水平
飞来的质量为mC,速度为v0的子弹击中,
且没有穿出,如图所示,求:以后运动
过程中弹簧的最大弹性势能。
把简单的事情做彻底,把平凡的事情做经典,把每一件小事都做得更精彩。
谢
谢
指
导
同课章节目录
