2020年秋沪科版七年级数学上册第3章《一次方程与方程组》综合能力检测卷(Word版无答案)
文档属性
| 名称 | 2020年秋沪科版七年级数学上册第3章《一次方程与方程组》综合能力检测卷(Word版无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 87.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-13 20:41:17 | ||
图片预览

文档简介
第3章 综合能力检测卷
时间:60分钟
满分:100分
一、选择题(每题3分,共30分)
1.下列方程是一元一次方程的是
( )
A.x2=25
B.x-5=6
C.x-y=6
D.=2
2.下列方程中,解为x=1的是
( )
A.x-1=-1
B.-2x=
C.x=-2
D.2x-1=1
3.已知3a=2b,则下列变形不正确的是
( )
A.3a+1=2b+1
B.9a=4b
C.=
D.2a=2b-a
4.解方程=1-时,去分母正确的是
( )
A.2(x-1)=1-(3x+1)
B.2(x-1)=6-3x+1
C.2x-1=6-3x+1
D.2(x-1)=6-(3x+1)
5.某校课外小组的学生分组做课外活动,若每组7人,则余下3人;若每组8人,则少5人.设课外小组的人数为x,分成的组数为y,下列方程组正确的是
( )
A.
B.
C.
D.
6.如果二元一次方程ax+by+2=0有两组解那么下列四个选项中仍是这个方程的解的是( )
A.
B.
C.
D.
7.若今年母女二人的年龄之和为56,10年前母亲的年龄是女儿的年龄的8倍,则10年前母亲的年龄为
( )
A.30岁
B.31岁
C.32岁
D.33岁
8.若方程组的解x和y的值互为相反数,则k的值为
( )
A.0
B.1
C.2
D.3
9.如果是方程组的解,那么下列各式中成立的是
( )
A.a+4c=2
B.4a+c=2
C.a+4c+2=0
D.4a+c+2=0
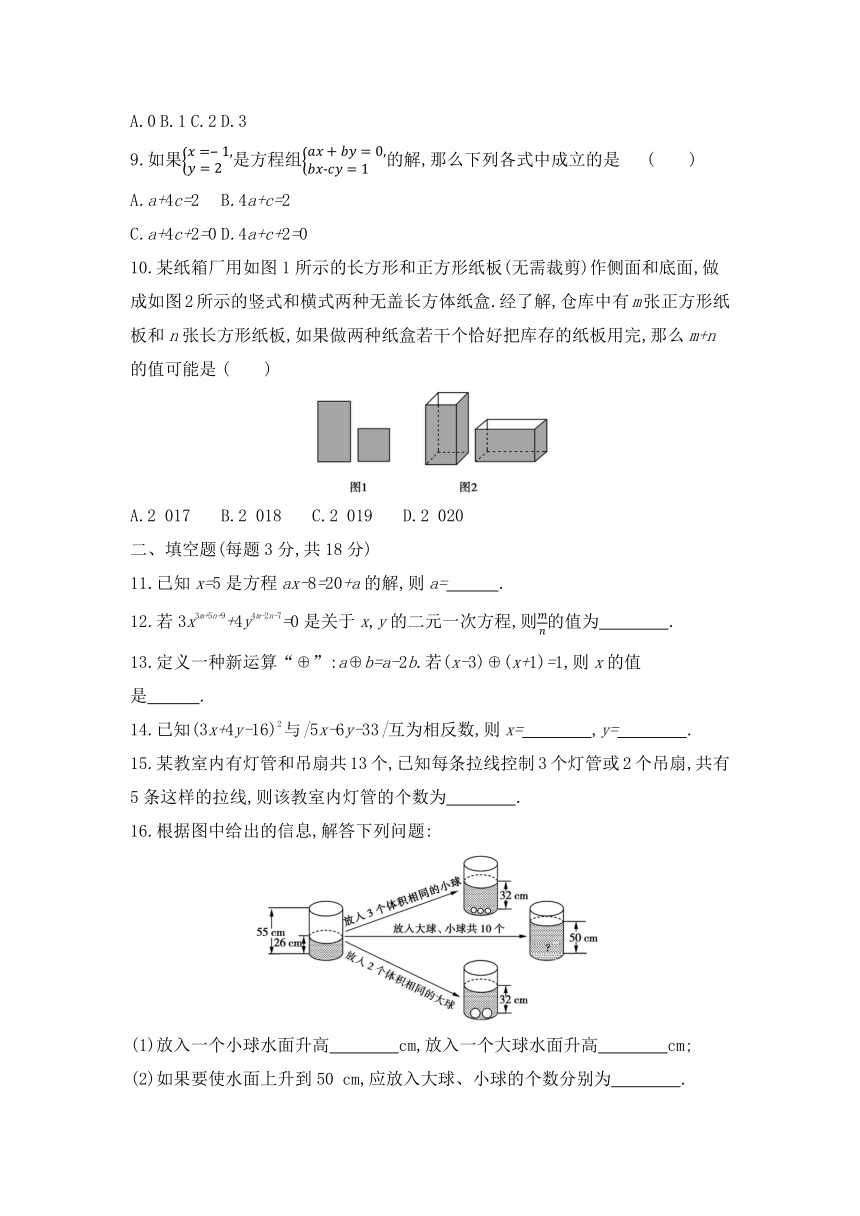
10.某纸箱厂用如图1所示的长方形和正方形纸板(无需裁剪)作侧面和底面,做成如图2所示的竖式和横式两种无盖长方体纸盒.经了解,仓库中有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个恰好把库存的纸板用完,那么m+n的值可能是
( )
A.2
017
B.2
018
C.2
019
D.2
020
二、填空题(每题3分,共18分)
11.已知x=5是方程ax-8=20+a的解,则a= .?
12.若3x3m+5n+9+4y4m-2n-7=0是关于x,y的二元一次方程,则的值为 .?
13.定义一种新运算“?”:a?b=a-2b.若(x-3)?(x+1)=1,则x的值是 .?
14.已知(3x+4y-16)2与|5x-6y-33|互为相反数,则x= ,y= .?
15.某教室内有灯管和吊扇共13个,已知每条拉线控制3个灯管或2个吊扇,共有5条这样的拉线,则该教室内灯管的个数为 .?
16.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 cm,放入一个大球水面升高 cm;?
(2)如果要使水面上升到50
cm,应放入大球、小球的个数分别为 .?
三、解答题(共52分)
17.(6分)解下列方程:
(1)1-3(6-x)=2(5-2x)+1; (2)-=2-.
18.(8分)解下列方程组:
(1)
(2)
19.(8分)定义新运算“
”,规定:x
y=ax2+by,其中a,b为常数.若1
2=5,2
1=6,求3
8的值.
20.(8分)已知关于x,y的方程组
(1)若方程组的解满足方程3x-4y=1,求k的值;
(2)请你给k一个值,使方程组的解中x,y都是正整数,并直接写出该方程组的解.
21.(10分)两个自行车队员进行训练,训练时1号队员与2号队员都以35
km/h的速度前进.突然,1号队员以45
km/h的速度离队独自行进,行进16
km后调转车头,仍以45
km/h的速度往回骑,直到与2号队员会合.
(1)1号队员从离队开始到与2号队员重新会合,经过了多长时间?
(2)1号队员从离队开始到与2号队员重新会合这个过程中,经过多长时间与2号队员相距1
km?
22.(12分)新房装修后,某居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称
单价/元
数量/个
金额/元
垃圾桶
15
鞋架
40
字画
m
2
90
合计
5
185
(1)居民购买垃圾桶、鞋架各几个?
(2)若居民再次购买字画和垃圾桶两种家居用品共花费150元,则有哪几种不同的购买方案?
时间:60分钟
满分:100分
一、选择题(每题3分,共30分)
1.下列方程是一元一次方程的是
( )
A.x2=25
B.x-5=6
C.x-y=6
D.=2
2.下列方程中,解为x=1的是
( )
A.x-1=-1
B.-2x=
C.x=-2
D.2x-1=1
3.已知3a=2b,则下列变形不正确的是
( )
A.3a+1=2b+1
B.9a=4b
C.=
D.2a=2b-a
4.解方程=1-时,去分母正确的是
( )
A.2(x-1)=1-(3x+1)
B.2(x-1)=6-3x+1
C.2x-1=6-3x+1
D.2(x-1)=6-(3x+1)
5.某校课外小组的学生分组做课外活动,若每组7人,则余下3人;若每组8人,则少5人.设课外小组的人数为x,分成的组数为y,下列方程组正确的是
( )
A.
B.
C.
D.
6.如果二元一次方程ax+by+2=0有两组解那么下列四个选项中仍是这个方程的解的是( )
A.
B.
C.
D.
7.若今年母女二人的年龄之和为56,10年前母亲的年龄是女儿的年龄的8倍,则10年前母亲的年龄为
( )
A.30岁
B.31岁
C.32岁
D.33岁
8.若方程组的解x和y的值互为相反数,则k的值为
( )
A.0
B.1
C.2
D.3
9.如果是方程组的解,那么下列各式中成立的是
( )
A.a+4c=2
B.4a+c=2
C.a+4c+2=0
D.4a+c+2=0
10.某纸箱厂用如图1所示的长方形和正方形纸板(无需裁剪)作侧面和底面,做成如图2所示的竖式和横式两种无盖长方体纸盒.经了解,仓库中有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个恰好把库存的纸板用完,那么m+n的值可能是
( )
A.2
017
B.2
018
C.2
019
D.2
020
二、填空题(每题3分,共18分)
11.已知x=5是方程ax-8=20+a的解,则a= .?
12.若3x3m+5n+9+4y4m-2n-7=0是关于x,y的二元一次方程,则的值为 .?
13.定义一种新运算“?”:a?b=a-2b.若(x-3)?(x+1)=1,则x的值是 .?
14.已知(3x+4y-16)2与|5x-6y-33|互为相反数,则x= ,y= .?
15.某教室内有灯管和吊扇共13个,已知每条拉线控制3个灯管或2个吊扇,共有5条这样的拉线,则该教室内灯管的个数为 .?
16.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 cm,放入一个大球水面升高 cm;?
(2)如果要使水面上升到50
cm,应放入大球、小球的个数分别为 .?
三、解答题(共52分)
17.(6分)解下列方程:
(1)1-3(6-x)=2(5-2x)+1; (2)-=2-.
18.(8分)解下列方程组:
(1)
(2)
19.(8分)定义新运算“
”,规定:x
y=ax2+by,其中a,b为常数.若1
2=5,2
1=6,求3
8的值.
20.(8分)已知关于x,y的方程组
(1)若方程组的解满足方程3x-4y=1,求k的值;
(2)请你给k一个值,使方程组的解中x,y都是正整数,并直接写出该方程组的解.
21.(10分)两个自行车队员进行训练,训练时1号队员与2号队员都以35
km/h的速度前进.突然,1号队员以45
km/h的速度离队独自行进,行进16
km后调转车头,仍以45
km/h的速度往回骑,直到与2号队员会合.
(1)1号队员从离队开始到与2号队员重新会合,经过了多长时间?
(2)1号队员从离队开始到与2号队员重新会合这个过程中,经过多长时间与2号队员相距1
km?
22.(12分)新房装修后,某居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称
单价/元
数量/个
金额/元
垃圾桶
15
鞋架
40
字画
m
2
90
合计
5
185
(1)居民购买垃圾桶、鞋架各几个?
(2)若居民再次购买字画和垃圾桶两种家居用品共花费150元,则有哪几种不同的购买方案?
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
