19.3.1 矩形的性质课件(共20张PPT)
文档属性
| 名称 | 19.3.1 矩形的性质课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-13 21:02:01 | ||
图片预览







文档简介
(共20张PPT)
19.3.1
矩形的性质
沪科版
八年级下
新知导入
问题1.黑板、电脑的显示屏是什么形状?
答:小学阶段我们称这些图形为长方形。
点拨:像这样的图形也就是矩形。
新知讲解
一、定义:有一个角是直角的平行四边形叫做矩形。
分析:有定义可知:一个四边形要成为矩形的条件为
①要有一个角是直角
②要是平行四边形。
由此可知:矩形是一种特殊的平行四边形,除具有一般平行四边形的性质外,它的边、角和对角线还具有哪些特殊的性质呢?
新知讲解
二、观察:画一个矩形,度量一下它的四条边长、两条对角线长以及四个角的度数,你能从中得出矩形特有的性质吗?
性质1.矩形的四个角都是直角.
已知:矩形ABCD
求证:∠A=∠B=∠C=∠D=900.
证明:由定义,矩形矩形必有一个角是直角,设∠A=900.
∵AB‖DC,AD‖BC
∴∠B=∠C=∠D=900.
即矩形ABCD的四个角都是直角.
B
C
A
D
新知讲解
三、由上述的度量可得:
性质2.矩形的对角线相等.
已知:如图,四边形ABCD
是矩形,对角线AC
与DB
相交于点O.
求证:AC=DB.
证明:∵四边形ABCD
是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
∵AB=DC,∠ABC=∠DCB,BC=
CB,
∴△ABC
≌
△DCB.
∴AC=DB.
D
新知讲解
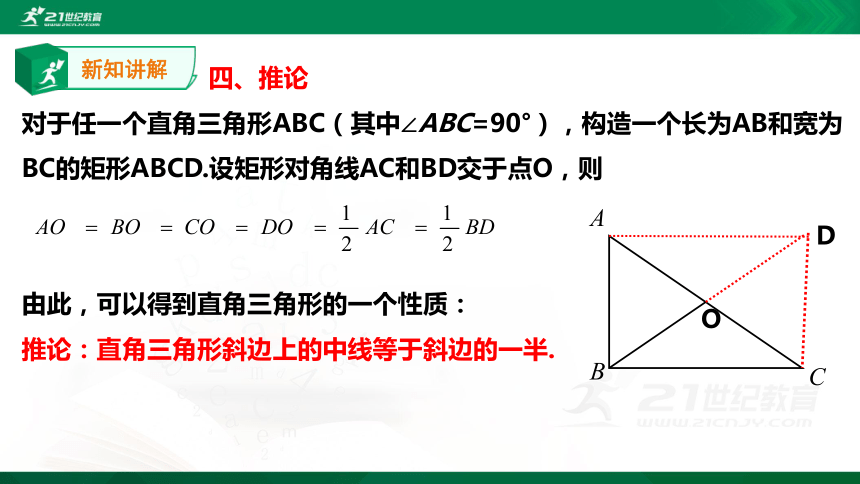
四、推论
对于任一个直角三角形ABC(其中∠ABC=90°),构造一个长为AB和宽为BC的矩形ABCD.设矩形对角线AC和BD交于点O,则
由此,可以得到直角三角形的一个性质:
推论:直角三角形斜边上的中线等于斜边的一半.
O
D
新知讲解
D
新知讲解
轴对称图形
2条
课堂练习
1.矩形具有而一般平行四边形不具有的性质是
(
)
A.对角线相等
B.对边相等
C.对角相等
D.对角线互相平分
2.若直角三角形的两条直角边分别5和12,则斜边上的中线长为
(
)
A.13
B.6
C.6.5
D.不能确定
A
C
课堂练习
3.如图,在矩形ABCD
中,对角线AC,BD
交于点O,
下列说法错误的是( )
A.AB∥DC
B.AC=BD
C.AC⊥BD
D.OA=OB
C
D
课堂练习
4.如图,在△ABC
中,∠ABC
=
90°,BD
是斜边AC
上的中线.
(1)若BD
=3cm,则AC
=_____cm;
(2)若∠C
=
30°
,AB
=
5cm,则AC
=_____cm,
BD
=
_____cm.
6
10
5
课堂练习
5.如图,EF
过矩形ABCD
对角线的交点O,且分别交AB、CD
于E、F,那么阴影部分的面积是矩形ABCD
面积的_________.
拓展提高
6.如图,四边形ABCD
是矩形,对角线AC,BD
相交于点O,BE∥AC
交DC
的延长线于点E.
(1)求证:BD=BE,
(2)若∠DBC=30°
,
BO=4
,求四边形ABED
的面积.
(1)证明:∵四边形ABCD
是矩形,
∴AC=
BD,AB∥CD.
又∵BE∥AC,
∴四边形ABEC
是平行四边形,
∴AC=BE,
∴BD=BE.
O
拓展提高
(2)解:∵在矩形ABCD
中,BO=4,
∴BD
=
2BO
=2×4=8.
∵∠DBC=30°,
∴CD=
BD=
×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=8.
在Rt△BCD
中,
∴四边形ABED
的面积=
×(4+8)×
=
.
0
中考连接
7.(南宁
中考)如图,在矩形ABCD
中,对角线AC,BD
交于点O,
∠AOB
=600,AB=2,则矩形的对角线AC长是(
)
A.
2
B.
4
C.
D
D
B
课堂总结
板书设计
19.3.1
矩形的性质
1.矩形性质1............
2.矩形性质2............
3.推论.....................
作业布置
课
本
P97
习
题
19.3
第
1
和
2
题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
19.3.1
矩形的性质
沪科版
八年级下
新知导入
问题1.黑板、电脑的显示屏是什么形状?
答:小学阶段我们称这些图形为长方形。
点拨:像这样的图形也就是矩形。
新知讲解
一、定义:有一个角是直角的平行四边形叫做矩形。
分析:有定义可知:一个四边形要成为矩形的条件为
①要有一个角是直角
②要是平行四边形。
由此可知:矩形是一种特殊的平行四边形,除具有一般平行四边形的性质外,它的边、角和对角线还具有哪些特殊的性质呢?
新知讲解
二、观察:画一个矩形,度量一下它的四条边长、两条对角线长以及四个角的度数,你能从中得出矩形特有的性质吗?
性质1.矩形的四个角都是直角.
已知:矩形ABCD
求证:∠A=∠B=∠C=∠D=900.
证明:由定义,矩形矩形必有一个角是直角,设∠A=900.
∵AB‖DC,AD‖BC
∴∠B=∠C=∠D=900.
即矩形ABCD的四个角都是直角.
B
C
A
D
新知讲解
三、由上述的度量可得:
性质2.矩形的对角线相等.
已知:如图,四边形ABCD
是矩形,对角线AC
与DB
相交于点O.
求证:AC=DB.
证明:∵四边形ABCD
是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
∵AB=DC,∠ABC=∠DCB,BC=
CB,
∴△ABC
≌
△DCB.
∴AC=DB.
D
新知讲解
四、推论
对于任一个直角三角形ABC(其中∠ABC=90°),构造一个长为AB和宽为BC的矩形ABCD.设矩形对角线AC和BD交于点O,则
由此,可以得到直角三角形的一个性质:
推论:直角三角形斜边上的中线等于斜边的一半.
O
D
新知讲解
D
新知讲解
轴对称图形
2条
课堂练习
1.矩形具有而一般平行四边形不具有的性质是
(
)
A.对角线相等
B.对边相等
C.对角相等
D.对角线互相平分
2.若直角三角形的两条直角边分别5和12,则斜边上的中线长为
(
)
A.13
B.6
C.6.5
D.不能确定
A
C
课堂练习
3.如图,在矩形ABCD
中,对角线AC,BD
交于点O,
下列说法错误的是( )
A.AB∥DC
B.AC=BD
C.AC⊥BD
D.OA=OB
C
D
课堂练习
4.如图,在△ABC
中,∠ABC
=
90°,BD
是斜边AC
上的中线.
(1)若BD
=3cm,则AC
=_____cm;
(2)若∠C
=
30°
,AB
=
5cm,则AC
=_____cm,
BD
=
_____cm.
6
10
5
课堂练习
5.如图,EF
过矩形ABCD
对角线的交点O,且分别交AB、CD
于E、F,那么阴影部分的面积是矩形ABCD
面积的_________.
拓展提高
6.如图,四边形ABCD
是矩形,对角线AC,BD
相交于点O,BE∥AC
交DC
的延长线于点E.
(1)求证:BD=BE,
(2)若∠DBC=30°
,
BO=4
,求四边形ABED
的面积.
(1)证明:∵四边形ABCD
是矩形,
∴AC=
BD,AB∥CD.
又∵BE∥AC,
∴四边形ABEC
是平行四边形,
∴AC=BE,
∴BD=BE.
O
拓展提高
(2)解:∵在矩形ABCD
中,BO=4,
∴BD
=
2BO
=2×4=8.
∵∠DBC=30°,
∴CD=
BD=
×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=8.
在Rt△BCD
中,
∴四边形ABED
的面积=
×(4+8)×
=
.
0
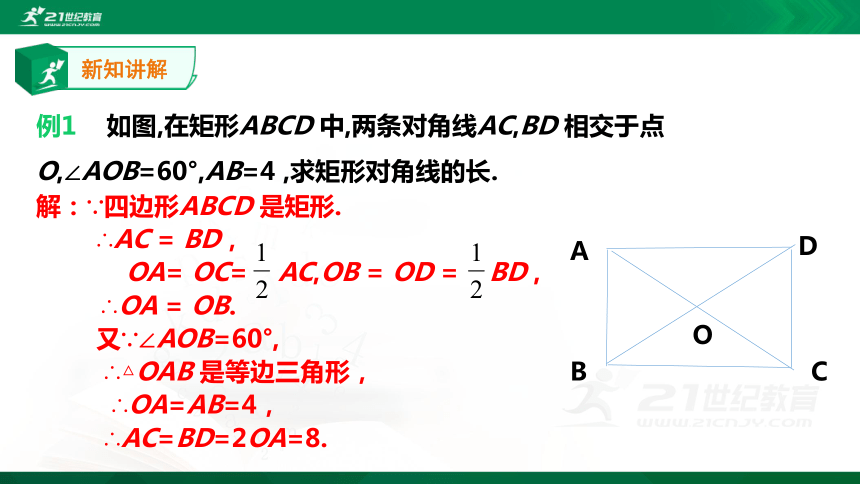
中考连接
7.(南宁
中考)如图,在矩形ABCD
中,对角线AC,BD
交于点O,
∠AOB
=600,AB=2,则矩形的对角线AC长是(
)
A.
2
B.
4
C.
D
D
B
课堂总结
板书设计
19.3.1
矩形的性质
1.矩形性质1............
2.矩形性质2............
3.推论.....................
作业布置
课
本
P97
习
题
19.3
第
1
和
2
题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
