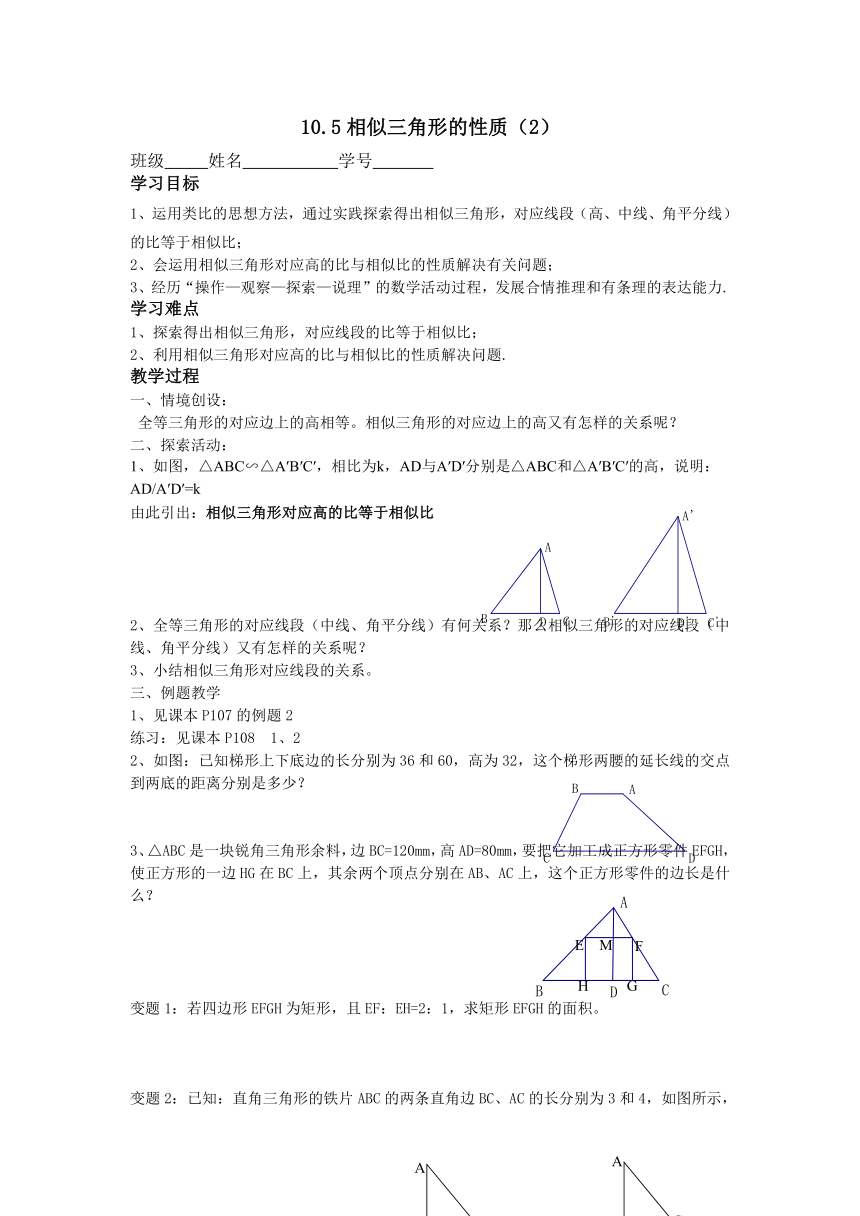
10.5相似三角形的性质（2）

10.5相似三角形的性质（2）
班级 姓名 学号
学习目标
1、运用类比的思想方法，通过实践探索得出相似三角形，对应线段（高、中线、角平分线）的比等于相似比；
2、会运用相似三角形对应高的比与相似比的性质解决有关问题；
3、经历“操作—观察—探索—说理”的数学活动过程，发展合情推理和有条理的表达能力.
学习难点
1、探索得出相似三角形，对应线段的比等于相似比；
2、利用相似三角形对应高的比与相似比的性质解决问题.
教学过程
一、情境创设：
全等三角形的对应边上的高相等。相似三角形的对应边上的高又有怎样的关系呢？
二、探索活动：
1、如图，△ABC∽△A′B′C′，相比为k，AD与A′D′分别是△ABC和△A′B′C′的高，说明：AD/A′D′=k
由此引出：相似三角形对应高的比等于相似比
2、全等三角形的对应线段（中线、角平分线）有何关系？那么相似三角形的对应线段（中线、角平分线）又有怎样的关系呢？
3、小结相似三角形对应线段的关系。
三、例题教学
1、见课本P107的例题2
练习：见课本P108 1、2
2、如图：已知梯形上下底边的长分别为36和60，高为32，这个梯形两腰的延长线的交点到两底的距离分别是多少？
3、△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成正方形零件EFGH，使正方形的一边HG在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是什么？
变题1：若四边形EFGH为矩形，且EF：EH=2：1，求矩形EFGH的面积。
变题2：已知：直角三角形的铁片ABC的两条直角边BC、AC的长分别为3和4，如图所示，分别采用（1）（2）两种方法，剪出一块正方形铁片，为使剪去正方形铁片后剩下的边角料较少，试比较哪种剪法较为合理，并说明理由。
4、如图，在△ABC中，AB=5，BC=4，AC=3，PQ∥AB，P点在AC上（与点A、C不重合），点Q在B、C上。
（1）当△PQC的面积与四边形PABQ的面积相等时，求CP的长；
（2）当△PQC的周长与四边形PABQ的周长相等时，求CP的长；
（3）在AB上是否存在点M，使得△PQM是等腰直角三角形？若存在，求出PQ的长。
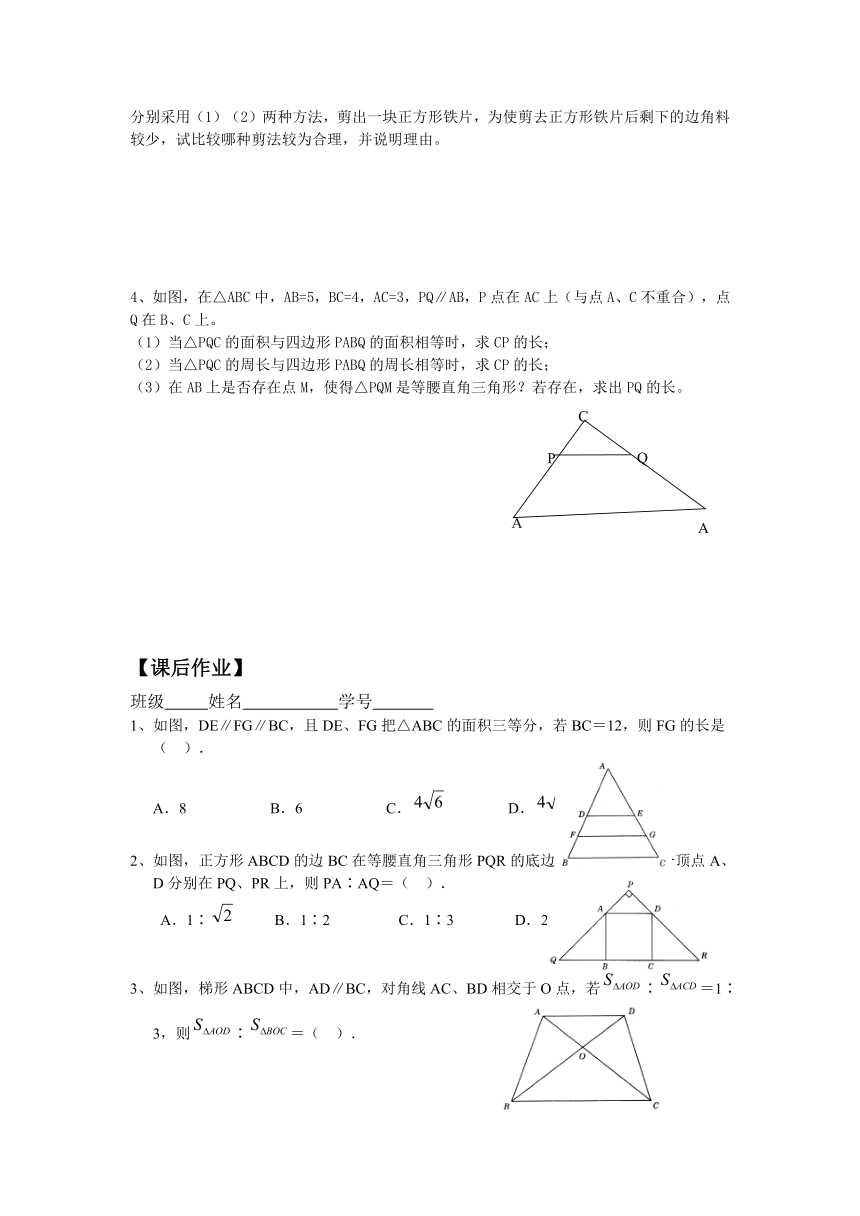
【课后作业】
班级 姓名 学号
1、如图，DE∥FG∥BC，且DE、FG把△ABC的面积三等分，若BC＝12，则FG的长是（　）．
　A．8　　　　　 B．6　　　　　 C．　　　　D．
　　
2、如图，正方形ABCD的边BC在等腰直角三角形PQR的底边QR上，其余两个顶点A、D分别在PQ、PR上，则PA∶AQ＝（　）．
　　A．1∶　　 B．1∶2　　　　 C．1∶3　　　　D．2∶3
3、如图，梯形ABCD中，AD∥BC，对角线AC、BD相交于O点，若∶＝1∶3，则∶＝（　）．
　　A．　　　　B．　　　　　C．　　　D．
4、在△ABC中，AB=9，AC=12，BC=18，D为AC上一点，DC=AC，在AB上取一点E，得到△ADE.若△ABC与△ADE相似，求 DE的长。
5、如图，在直角梯形ABCD中，AD∥BC,∠A=90°,AB=7,AD=2,BC=3,如果边AB上的点P使得以P、A、D为顶点的三角形与以P、B、C为顶点的三角形相似，求AP的长。
如图，在△ABC中,AB=AC=1,点D、E在直线BC上运动，设BD=,CE=.
如果∠BAC=30°，∠DAE=105°，试确定与之间的函数关系。
7、如图，中，D、E是CB上两点，且AC=CD=DE=EB，图中有相似三角形吗？如果有，请指出来并给予证明，如果没有，请说明理由。
8、如图，路灯（点）距地面8米，身高1.6米的小明从距路灯的底部（点 ）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？
9、已知，延长BC到D，使．取的中点，连结交于点．
（1）求 ( http: / / www. / )的值；
（2）若，求的长．
E
F
H
G
M
C
B
F
G
A
D
E
A
D
C
F
B
E
（1）
（2）
A
A
P
Q
C
A
B
C
D
P
E
A
D
B
C
A
B
C
D
E
P
O
B
N
A
M
A
B
F
E
C
D