人教版八年级下册数学:19.2.2 一次函数的应用课件 (共19张PPT)
文档属性
| 名称 | 人教版八年级下册数学:19.2.2 一次函数的应用课件 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-14 20:09:49 | ||
图片预览

文档简介
(共19张PPT)
一次函数的应用
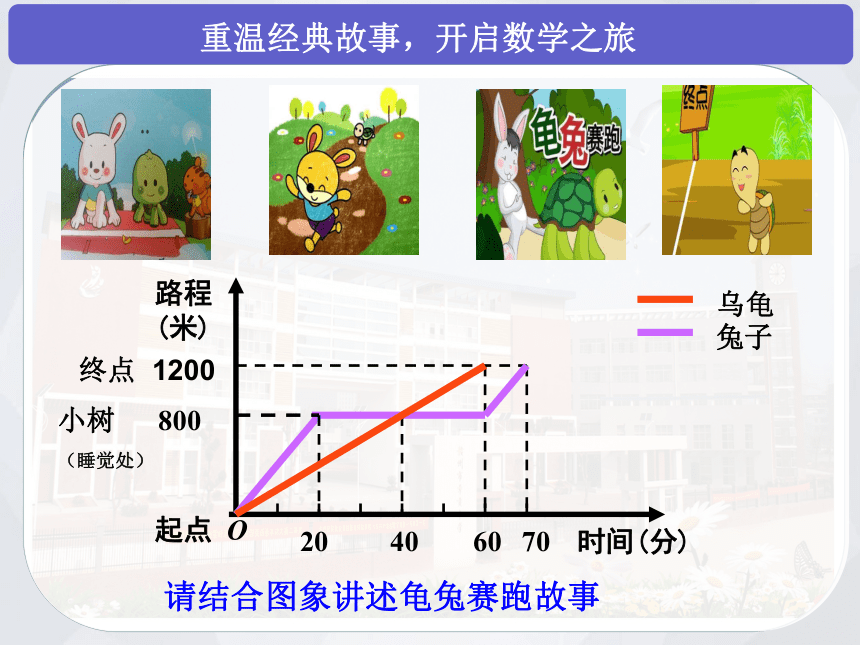
重温经典故事,开启数学之旅
请结合图象讲述龟兔赛跑故事
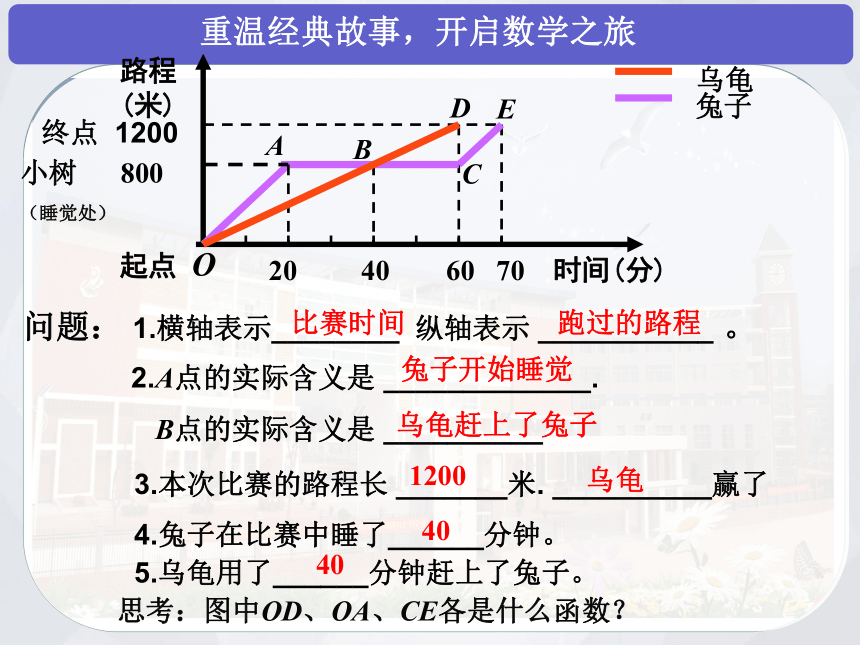
3.本次比赛的路程长
_______米.
__________赢了
1200
4.兔子在比赛中睡了______分钟。
乌龟
5.乌龟用了______分钟赶上了兔子。
40
40
问题:
1.横轴表示________
纵轴表示
___________
。
比赛时间
跑过的路程
A
B
2.A点的实际含义是
_____________.
B点的实际含义是
__________
兔子开始睡觉
乌龟赶上了兔子
C
D
E
重温经典故事,开启数学之旅
思考:图中OD、OA、CE各是什么函数?
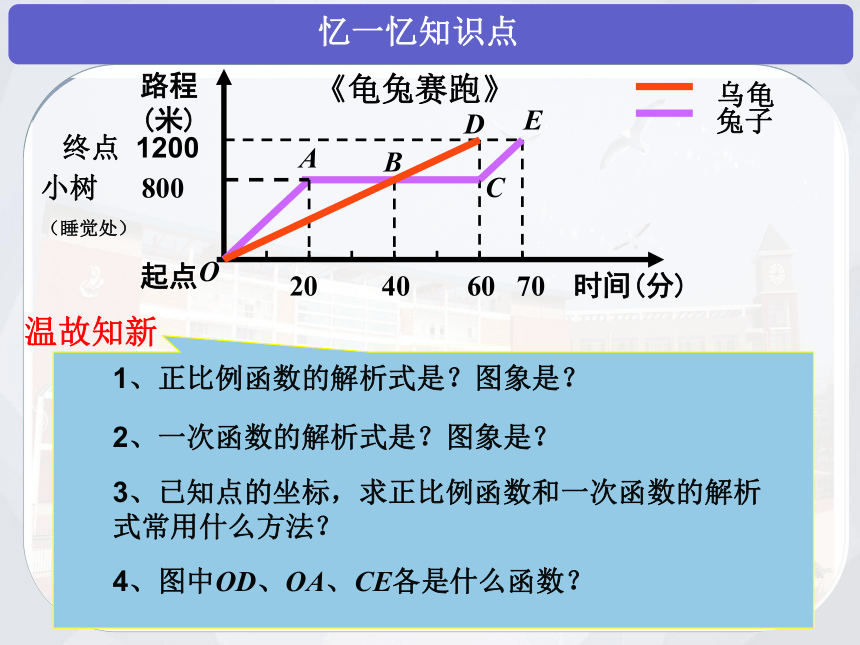
《龟兔赛跑》
温故知新
1、正比例函数的解析式是?图象是?
3、已知点的坐标,求正比例函数和一次函数的解析式常用什么方法?
忆一忆知识点
2、一次函数的解析式是?图象是?
A
O
B
C
D
E
4、图中OD、OA、CE各是什么函数?
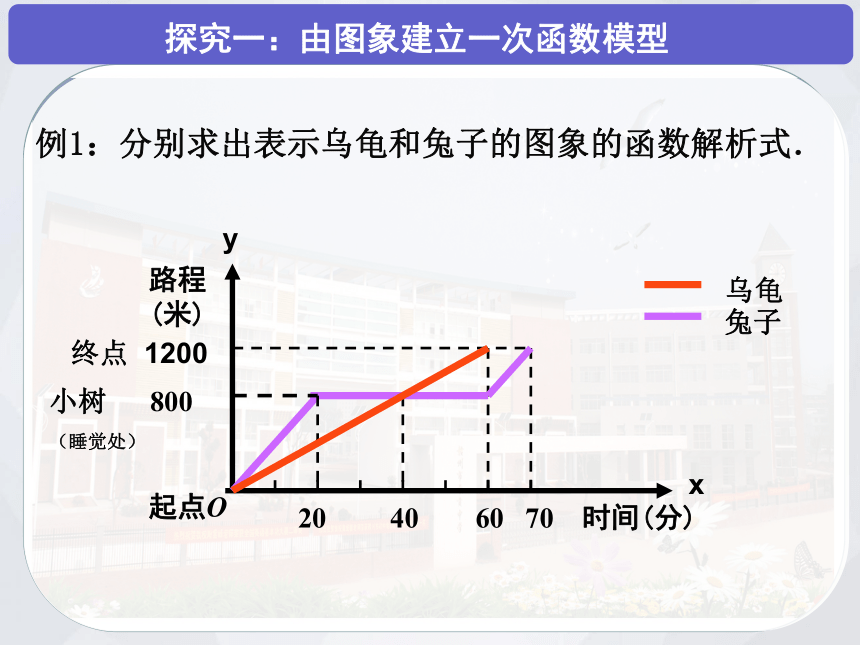
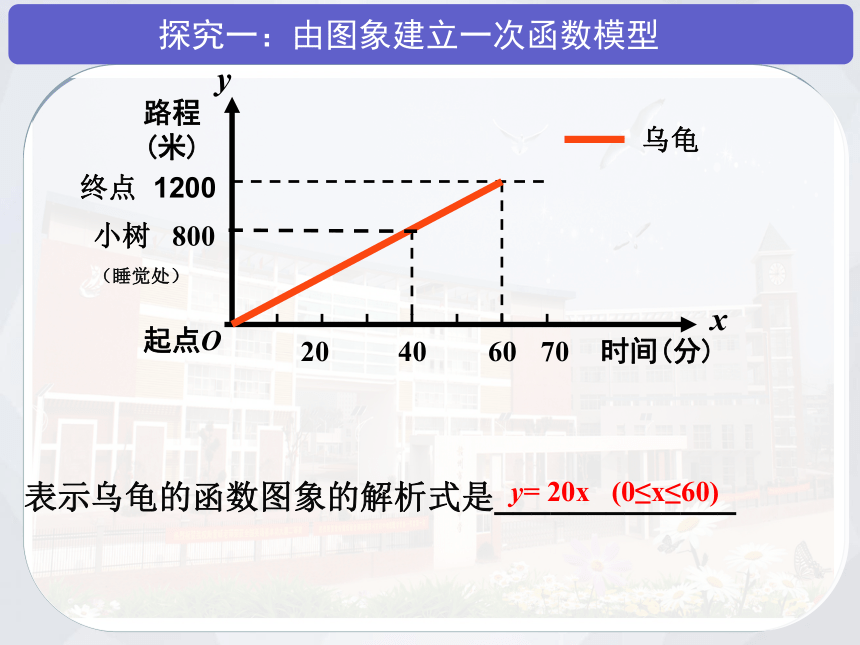
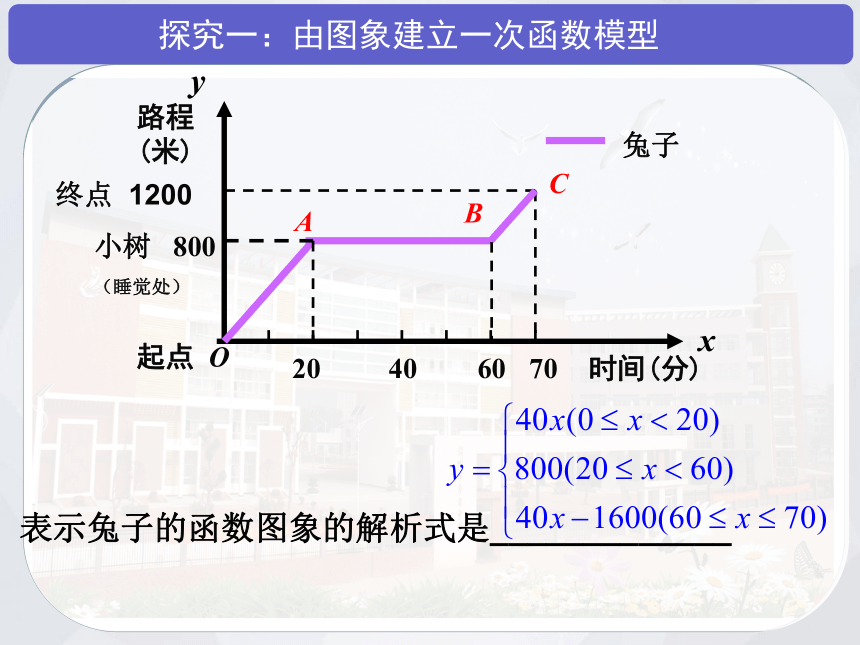
探究一:由图象建立一次函数模型
例1:分别求出表示乌龟和兔子的图象的函数解析式.
x
y
表示乌龟的函数图象的解析式是_____________
探究一:由图象建立一次函数模型
y=
20x
(0≤x≤60)
表示兔子的函数图象的解析式是_____________
探究一:由图象建立一次函数模型
C
B
A
跟踪练习1
某长途汽车客运公司规定:旅客可随身携带一定重量的行李,如果超过规定,则需要购买行李票,行李票费用y(元)是行李重量x(千克)的一次函数,其图象如图所示。
(1)当x=60时,y=_________
(2)y与x之间的函数关系式.
(3)旅客最多可免费携带行李的千克数.
6
y=0.2x-6
30
《龟兔赛跑》
学有所得
读懂函数图象要注意以下几点:
(1)理解横轴与纵轴的实际意义;
(2)关注特殊点(如交点)与特殊线段(如平行于坐标轴的线段)的实际意义;
(3)图象是什么函数及自变量的取值范围.
小结与归纳
D
A
B
C
例2.鞋子的鞋码和鞋长存在一种换算关系,下表是几组鞋码与鞋长换算的对应数值:
(1)观察与猜想:鞋码y与鞋长x之间的关系是______函数关系.
(2)此函数的解析式是___________________
(3)小明目前穿25cm的鞋,他爸爸去外地出差时帮小明买了一双42码的鞋,请问这双鞋目前小明穿着合脚吗?若不合脚,应该买多大鞋码的鞋?
y=2x-10
解:当y=42时,42=2x-10,
解得
x=26﹥25,所以不合脚.
当x=25时,y=2×25-10=40
应该买40码的鞋.
一次
探究二:由表格建立一次函数模型
鞋长
x
(
cm)
16
19
21
24
鞋码
y
(码)
22
28
32
38
跟踪练习2
某商店售货时,其数量x与售价y的关系如表所示:
则y与x的函数关系式是(
)
B
数量x/kg
售价y/元
1
8.4
2
16.4
3
24.4
…
…
探究三:由实际问题建立一次函数模型
例3:某市为了鼓励市民节约用水,采取分段收费标准,若每月用水量不超过5吨,则每吨2元,若每月用水量超过5吨,则超过部分按每吨3元收费。设每月用水量是x吨,应交水费y元。
(1)写出y与x之间的函数解析式。
(2)若某居民该月用水3.5吨,则应交水费多少元?
若该月交水费13元,则用水多少吨?
解:(1)当0
≤x≤5时的函数解析式为:y=2x
当x>5时的函数解析式为:y=3x-5
(2)当用水3.5吨时,3.5﹤5,则应交水费
y=2×3.5=7(元).
若该月交水费13元,13>10,所以用水量x>5吨,3x-5=13,
所以
x=6,则用水6吨.
跟踪练习3
某市出租车公司收费标准是:3公里之内(含3公里)5元,超出3公里部分,每公里2元.
(1)请写出乘车费用y(元)与所行路程x(公里)之间的函数关系式.
(2)小明有19元钱,他乘此出租车最远能到达_____公里处.
解:(1)当
0≤
x≤3时的函数解析式为:y=5
当x>3时的函数解析式为:y=2(x-3)+5,化简得:
y=2x-1
10
(2)当
y=19时,y>5,所以乘车路程超过3公里,即x>3,把y=19
代入y=2(x-3)+5中,得:
19=2x-1,解得:x
=10
我的玉米便宜卖,10元2千克,超过2千克部分的玉米价格打8折。
您的玉米怎么卖呢?
能力提升
综合应用
(1)请根据对话,完成下列表格。
18
5
(2)请写出付款金额y元与购买量x之间的函数关系式。
解:当
0≤
x≤2时的函数解析式为:y=5x
当
x>2时的函数解析式为:y=5×
0.8(x-2)+10,化简得:
y=4x+2
付款金额(元)
10
购买量(千克)
1
2
4
能力提升
综合应用
(1)请根据对话,完成下列表格。
18
5
(2)请写出付款金额y元与购买量x之间的函数关系式。
解:当
0≤
x≤2时的函数解析式为:y=5x
当x>2时的函数解析式为:y=5×
0.8(x-2)+10,化简得:
y=4x+2
(3)请选择一个符合题意的函数图象。(
)
A
付款金额(元)
10
购买量(千克)
1
2
4
(5)玉米买回家后,妈妈发现很可口,于是又拿了18元叫她再去买玉米,小红想了想,如果一次性购买26元的玉米,会比先买8元玉米,再买18元玉米这种买法更实惠,
请你帮她算算,这两种买法,相差多少
玉米?
(4)小红的妈妈拿了8元钱叫她买玉米,请问能买到多少玉米?
8÷5=1.6,能买到1.6千克玉米
解:若买两次,则8÷5=1.6,4x+2=18,解得
x=4,
合计:4+1.6=5.6,
若买一次,则
4x+2=26,解得
x=6
相差:6-5.6=0.4,所以相差0.4千克玉米。
能力提升
综合应用
(2)请写出付款金额y元与购买量x之间的函数关系式。
解:当
0≤
x≤2时的函数解析式为:y=5x
当x>2时的函数解析式为:y=5×
0.8(x-2)+10,化简得:
y=4x+2
课堂小结
模型:一次函数
方法:建立数学模型
数学思想:
数形结合
图象法,列表法,解析法
互相转化
应用意识:
数学“源于生活、寓于生活、用于生活”
课后作业
创新:
P71,
T1,
P72
T1-T5
一次函数的应用
重温经典故事,开启数学之旅
请结合图象讲述龟兔赛跑故事
3.本次比赛的路程长
_______米.
__________赢了
1200
4.兔子在比赛中睡了______分钟。
乌龟
5.乌龟用了______分钟赶上了兔子。
40
40
问题:
1.横轴表示________
纵轴表示
___________
。
比赛时间
跑过的路程
A
B
2.A点的实际含义是
_____________.
B点的实际含义是
__________
兔子开始睡觉
乌龟赶上了兔子
C
D
E
重温经典故事,开启数学之旅
思考:图中OD、OA、CE各是什么函数?
《龟兔赛跑》
温故知新
1、正比例函数的解析式是?图象是?
3、已知点的坐标,求正比例函数和一次函数的解析式常用什么方法?
忆一忆知识点
2、一次函数的解析式是?图象是?
A
O
B
C
D
E
4、图中OD、OA、CE各是什么函数?
探究一:由图象建立一次函数模型
例1:分别求出表示乌龟和兔子的图象的函数解析式.
x
y
表示乌龟的函数图象的解析式是_____________
探究一:由图象建立一次函数模型
y=
20x
(0≤x≤60)
表示兔子的函数图象的解析式是_____________
探究一:由图象建立一次函数模型
C
B
A
跟踪练习1
某长途汽车客运公司规定:旅客可随身携带一定重量的行李,如果超过规定,则需要购买行李票,行李票费用y(元)是行李重量x(千克)的一次函数,其图象如图所示。
(1)当x=60时,y=_________
(2)y与x之间的函数关系式.
(3)旅客最多可免费携带行李的千克数.
6
y=0.2x-6
30
《龟兔赛跑》
学有所得
读懂函数图象要注意以下几点:
(1)理解横轴与纵轴的实际意义;
(2)关注特殊点(如交点)与特殊线段(如平行于坐标轴的线段)的实际意义;
(3)图象是什么函数及自变量的取值范围.
小结与归纳
D
A
B
C
例2.鞋子的鞋码和鞋长存在一种换算关系,下表是几组鞋码与鞋长换算的对应数值:
(1)观察与猜想:鞋码y与鞋长x之间的关系是______函数关系.
(2)此函数的解析式是___________________
(3)小明目前穿25cm的鞋,他爸爸去外地出差时帮小明买了一双42码的鞋,请问这双鞋目前小明穿着合脚吗?若不合脚,应该买多大鞋码的鞋?
y=2x-10
解:当y=42时,42=2x-10,
解得
x=26﹥25,所以不合脚.
当x=25时,y=2×25-10=40
应该买40码的鞋.
一次
探究二:由表格建立一次函数模型
鞋长
x
(
cm)
16
19
21
24
鞋码
y
(码)
22
28
32
38
跟踪练习2
某商店售货时,其数量x与售价y的关系如表所示:
则y与x的函数关系式是(
)
B
数量x/kg
售价y/元
1
8.4
2
16.4
3
24.4
…
…
探究三:由实际问题建立一次函数模型
例3:某市为了鼓励市民节约用水,采取分段收费标准,若每月用水量不超过5吨,则每吨2元,若每月用水量超过5吨,则超过部分按每吨3元收费。设每月用水量是x吨,应交水费y元。
(1)写出y与x之间的函数解析式。
(2)若某居民该月用水3.5吨,则应交水费多少元?
若该月交水费13元,则用水多少吨?
解:(1)当0
≤x≤5时的函数解析式为:y=2x
当x>5时的函数解析式为:y=3x-5
(2)当用水3.5吨时,3.5﹤5,则应交水费
y=2×3.5=7(元).
若该月交水费13元,13>10,所以用水量x>5吨,3x-5=13,
所以
x=6,则用水6吨.
跟踪练习3
某市出租车公司收费标准是:3公里之内(含3公里)5元,超出3公里部分,每公里2元.
(1)请写出乘车费用y(元)与所行路程x(公里)之间的函数关系式.
(2)小明有19元钱,他乘此出租车最远能到达_____公里处.
解:(1)当
0≤
x≤3时的函数解析式为:y=5
当x>3时的函数解析式为:y=2(x-3)+5,化简得:
y=2x-1
10
(2)当
y=19时,y>5,所以乘车路程超过3公里,即x>3,把y=19
代入y=2(x-3)+5中,得:
19=2x-1,解得:x
=10
我的玉米便宜卖,10元2千克,超过2千克部分的玉米价格打8折。
您的玉米怎么卖呢?
能力提升
综合应用
(1)请根据对话,完成下列表格。
18
5
(2)请写出付款金额y元与购买量x之间的函数关系式。
解:当
0≤
x≤2时的函数解析式为:y=5x
当
x>2时的函数解析式为:y=5×
0.8(x-2)+10,化简得:
y=4x+2
付款金额(元)
10
购买量(千克)
1
2
4
能力提升
综合应用
(1)请根据对话,完成下列表格。
18
5
(2)请写出付款金额y元与购买量x之间的函数关系式。
解:当
0≤
x≤2时的函数解析式为:y=5x
当x>2时的函数解析式为:y=5×
0.8(x-2)+10,化简得:
y=4x+2
(3)请选择一个符合题意的函数图象。(
)
A
付款金额(元)
10
购买量(千克)
1
2
4
(5)玉米买回家后,妈妈发现很可口,于是又拿了18元叫她再去买玉米,小红想了想,如果一次性购买26元的玉米,会比先买8元玉米,再买18元玉米这种买法更实惠,
请你帮她算算,这两种买法,相差多少
玉米?
(4)小红的妈妈拿了8元钱叫她买玉米,请问能买到多少玉米?
8÷5=1.6,能买到1.6千克玉米
解:若买两次,则8÷5=1.6,4x+2=18,解得
x=4,
合计:4+1.6=5.6,
若买一次,则
4x+2=26,解得
x=6
相差:6-5.6=0.4,所以相差0.4千克玉米。
能力提升
综合应用
(2)请写出付款金额y元与购买量x之间的函数关系式。
解:当
0≤
x≤2时的函数解析式为:y=5x
当x>2时的函数解析式为:y=5×
0.8(x-2)+10,化简得:
y=4x+2
课堂小结
模型:一次函数
方法:建立数学模型
数学思想:
数形结合
图象法,列表法,解析法
互相转化
应用意识:
数学“源于生活、寓于生活、用于生活”
课后作业
创新:
P71,
T1,
P72
T1-T5
