人教版数学八年级下册:17.1.3 勾股定理的应用课件 (共16张PPT)
文档属性
| 名称 | 人教版数学八年级下册:17.1.3 勾股定理的应用课件 (共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-15 18:52:57 | ||
图片预览




文档简介
(共16张PPT)
1.已知直角三角形ABC的两直角边分别为a、b,斜边为c
,则
a、b、c
三者之间的关系是
;
2.若一个直角三角形两条直角边长是3和2,那么第三条边长是
;
3.
叫做无理数.
a2+b2=c2
无限不循环小数
17.1.3
勾股定理的应用
1.能用勾股定理证明直角三角形全等的“斜边、
直角边”判定定理;
2.能应用勾股定理在数轴上画出表示无理数的点;
3.体会勾股定理在数学中的地位和作用.
重点:利用勾股定理在数轴上表示无理数。
难点:确定以无理数为斜边的直角三角形的两条直
角边长。
问题思考
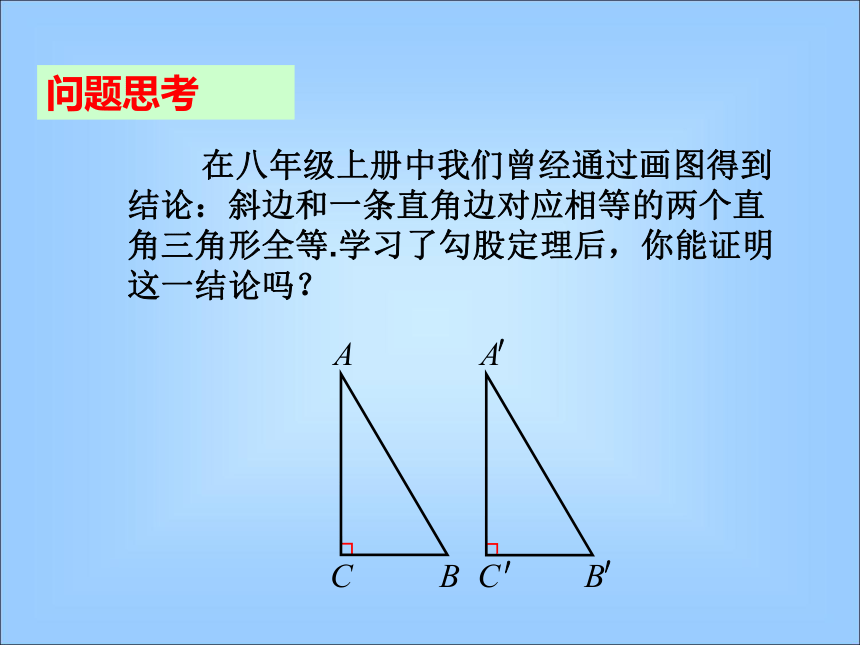
在八年级上册中我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
证明“HL”
∵
AB=A
B
,
AC=A
C
,
∴ BC=B
C
.
∴ △ABC≌△A
B
C
(SSS).
B
A
D
C
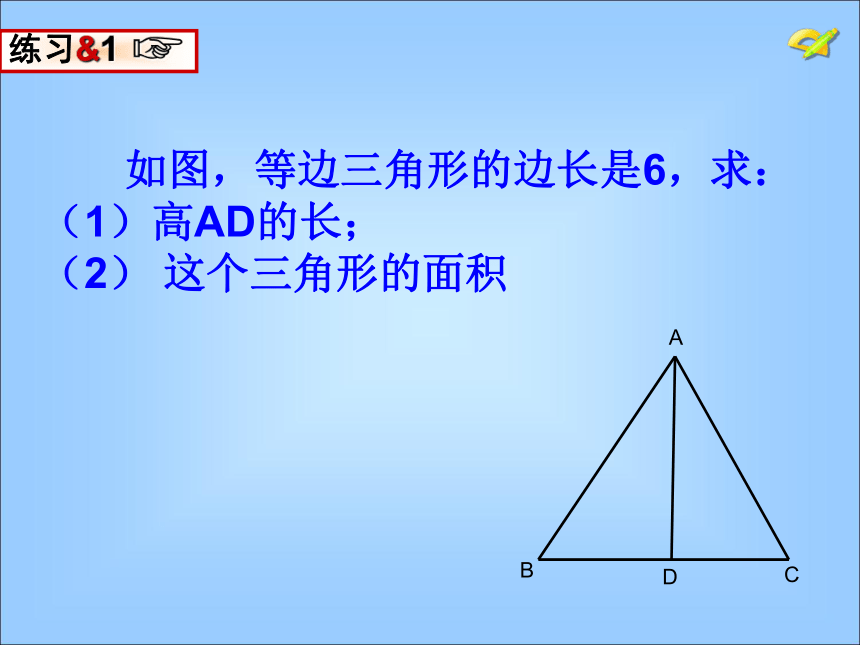
如图,等边三角形的边长是6,求:(1)高AD的长;
(2)
这个三角形的面积
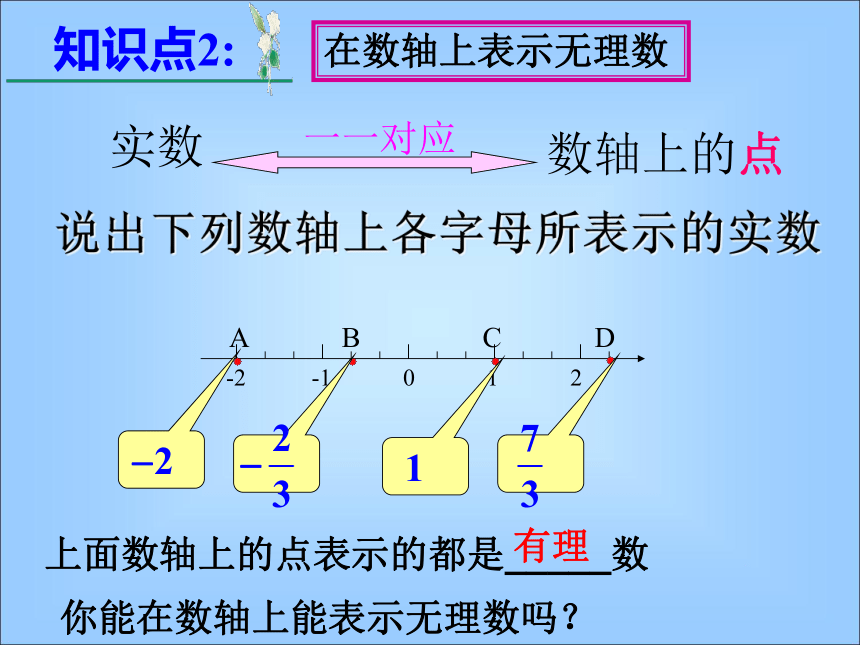
说出下列数轴上各字母所表示的实数
实数
数轴上的点
一一对应
上面数轴上的点表示的都是_____数
你能在数轴上能表示无理数吗?
有理
在数轴上表示无理数
你能在数轴上表示出
的点吗?
在数学中也有这样一幅美丽的“海螺型”图案
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
第七届国际数学
教育大会的会徽
1
数学海螺图:
√
√
0
1
2
3
4
步骤:
l
A
B
C
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
0
1
2
3
4
l
A
B
C
√
√
0
1
2
3
4
A
B
C
学习体会
1.本节课你有哪些收获?你对勾股定理又有了多少新的认识?
2.预习时的疑难问题解决了吗?你还有哪些疑惑?
3.你认为本节还有哪些需要注意的地方?
如图,在△ABC中,∠ACB=900,CD⊥AB,垂足为D,若∠B=300,AD=1求高CD和△ABC的面积。
C
A
B
D
1
2
3
双垂图
观察右图,分析各式,然后解答问题:
(1)用含有n(n是正整数)
的等式表示上述变化规律;
(2)推算出OA10的长;
作业布置
必做题:教材第29页习题17.1第11、12题.
选做题:
教材习题17.1第14题.
1.已知直角三角形ABC的两直角边分别为a、b,斜边为c
,则
a、b、c
三者之间的关系是
;
2.若一个直角三角形两条直角边长是3和2,那么第三条边长是
;
3.
叫做无理数.
a2+b2=c2
无限不循环小数
17.1.3
勾股定理的应用
1.能用勾股定理证明直角三角形全等的“斜边、
直角边”判定定理;
2.能应用勾股定理在数轴上画出表示无理数的点;
3.体会勾股定理在数学中的地位和作用.
重点:利用勾股定理在数轴上表示无理数。
难点:确定以无理数为斜边的直角三角形的两条直
角边长。
问题思考
在八年级上册中我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
证明“HL”
∵
AB=A
B
,
AC=A
C
,
∴ BC=B
C
.
∴ △ABC≌△A
B
C
(SSS).
B
A
D
C
如图,等边三角形的边长是6,求:(1)高AD的长;
(2)
这个三角形的面积
说出下列数轴上各字母所表示的实数
实数
数轴上的点
一一对应
上面数轴上的点表示的都是_____数
你能在数轴上能表示无理数吗?
有理
在数轴上表示无理数
你能在数轴上表示出
的点吗?
在数学中也有这样一幅美丽的“海螺型”图案
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
第七届国际数学
教育大会的会徽
1
数学海螺图:
√
√
0
1
2
3
4
步骤:
l
A
B
C
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
0
1
2
3
4
l
A
B
C
√
√
0
1
2
3
4
A
B
C
学习体会
1.本节课你有哪些收获?你对勾股定理又有了多少新的认识?
2.预习时的疑难问题解决了吗?你还有哪些疑惑?
3.你认为本节还有哪些需要注意的地方?
如图,在△ABC中,∠ACB=900,CD⊥AB,垂足为D,若∠B=300,AD=1求高CD和△ABC的面积。
C
A
B
D
1
2
3
双垂图
观察右图,分析各式,然后解答问题:
(1)用含有n(n是正整数)
的等式表示上述变化规律;
(2)推算出OA10的长;
作业布置
必做题:教材第29页习题17.1第11、12题.
选做题:
教材习题17.1第14题.
