沪科版七年级下册数学:10.1相交线(第1课时)课件 (17张PPT)
文档属性
| 名称 | 沪科版七年级下册数学:10.1相交线(第1课时)课件 (17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-15 19:56:32 | ||
图片预览





文档简介
(共17张PPT)
10.1
相交线(第1课时)
生活不缺乏美,
缺乏的是发现美的眼光
平行线
铁轨
双杠
筷子
剪刀
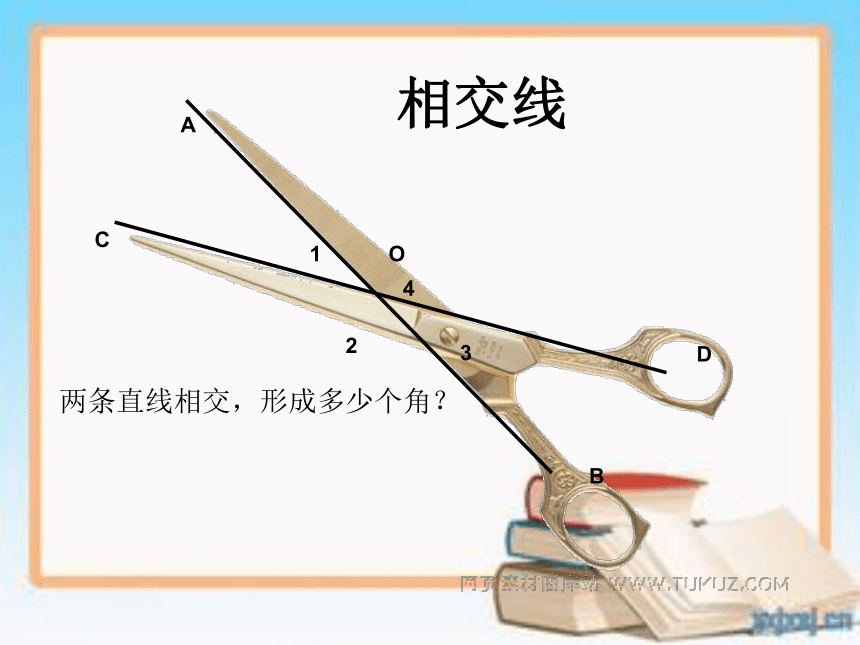
相交线
两条直线相交,形成多少个角?
D
C
O
3
4
2
1
)
)
)
)
对顶角定义:
直线AB与CD相交于点O
,
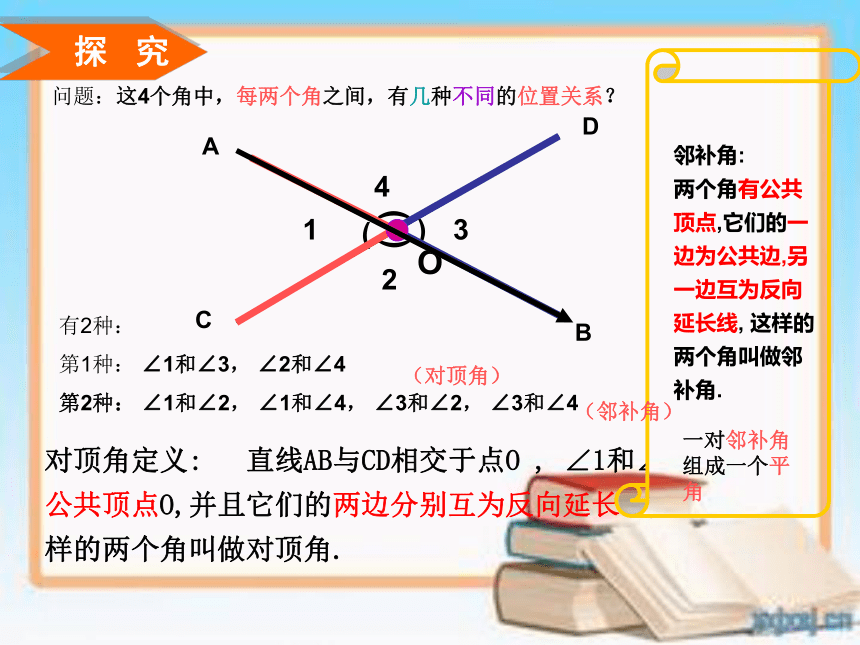
∠1和∠3有公共顶点O,并且它们的两边分别互为反向延长线,这样的两个角叫做对顶角.
探
究
问题:这4个角中,每两个角之间,有几种不同的位置关系?
有2种:
第1种:
∠1和∠3,
∠2和∠4
第2种:
∠1和∠2,
∠1和∠4,
∠3和∠2,
∠3和∠4
(对顶角)
(邻补角)
一对邻补角组成一个平角
对顶角
判断下列各图中∠1与∠2是否为对顶角,
并说明理由.
探
究
D
C
O
探
究
问题:1.一对邻补角之间有什么数量关系?
2.一对对顶角之间有什么数量关系?
为什么?
性质:
1.邻补角相加等于180度
如:
∠1+∠2=180°,∠3+∠4=180°(本质:1个平角=180
°)
2.对顶角相等
如:
∠1=
∠3,
∠2
=∠4
D
C
O
解
∵
∠1+∠2=180°,∠3+∠2=180°
?
?
∴
∠1=
∠3
(平角定义)
(同角的补角相等)
例1:已知直线a,b相交,
∠1=400则∠2=______,
∠3=______,
∠4=______.
例题分析
140°
40°
140°
直线AB、CD相交于O,OB
平分∠DOE,
∠DOE
=600,则∠AOC=
.
D
E
O
C
B
A
(
300
拓展延伸
回归生活
A
C
B
星期天,小刚和爸爸一起去河边钓鱼,河对岸有两棵树A,B,河边有一棵树C,结合平时的学习,小刚想出来一个问题“如何测量∠ACB的大小?”你能解答这个问题吗?
D
E
课堂小结
1.本节课你学到了什么?
2.
你有什么体会?
3条直线AB,CD,EF交与点O,请回答下面问题:
练习巩固
A
C
E
F
D
B
O
(1)图中有______对对顶角?
6
(2)4条直线相交于点O,共有___对对顶角?
5条直线相交于点O,共有___对对顶角?
n条直线相交于点O,共有___对对顶角?
关键:1:2条直线相交,产生2对对顶角
2:
看图中有(?)组“2条直线相交”
作
业
必做题:习题10.1
第1.2题
选做题:直线AB,CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°,∠EOF=_____
C
E
F
D
B
O
A
10.1
相交线(第1课时)
生活不缺乏美,
缺乏的是发现美的眼光
平行线
铁轨
双杠
筷子
剪刀
相交线
两条直线相交,形成多少个角?
D
C
O
3
4
2
1
)
)
)
)
对顶角定义:
直线AB与CD相交于点O
,
∠1和∠3有公共顶点O,并且它们的两边分别互为反向延长线,这样的两个角叫做对顶角.
探
究
问题:这4个角中,每两个角之间,有几种不同的位置关系?
有2种:
第1种:
∠1和∠3,
∠2和∠4
第2种:
∠1和∠2,
∠1和∠4,
∠3和∠2,
∠3和∠4
(对顶角)
(邻补角)
一对邻补角组成一个平角
对顶角
判断下列各图中∠1与∠2是否为对顶角,
并说明理由.
探
究
D
C
O
探
究
问题:1.一对邻补角之间有什么数量关系?
2.一对对顶角之间有什么数量关系?
为什么?
性质:
1.邻补角相加等于180度
如:
∠1+∠2=180°,∠3+∠4=180°(本质:1个平角=180
°)
2.对顶角相等
如:
∠1=
∠3,
∠2
=∠4
D
C
O
解
∵
∠1+∠2=180°,∠3+∠2=180°
?
?
∴
∠1=
∠3
(平角定义)
(同角的补角相等)
例1:已知直线a,b相交,
∠1=400则∠2=______,
∠3=______,
∠4=______.
例题分析
140°
40°
140°
直线AB、CD相交于O,OB
平分∠DOE,
∠DOE
=600,则∠AOC=
.
D
E
O
C
B
A
(
300
拓展延伸
回归生活
A
C
B
星期天,小刚和爸爸一起去河边钓鱼,河对岸有两棵树A,B,河边有一棵树C,结合平时的学习,小刚想出来一个问题“如何测量∠ACB的大小?”你能解答这个问题吗?
D
E
课堂小结
1.本节课你学到了什么?
2.
你有什么体会?
3条直线AB,CD,EF交与点O,请回答下面问题:
练习巩固
A
C
E
F
D
B
O
(1)图中有______对对顶角?
6
(2)4条直线相交于点O,共有___对对顶角?
5条直线相交于点O,共有___对对顶角?
n条直线相交于点O,共有___对对顶角?
关键:1:2条直线相交,产生2对对顶角
2:
看图中有(?)组“2条直线相交”
作
业
必做题:习题10.1
第1.2题
选做题:直线AB,CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°,∠EOF=_____
C
E
F
D
B
O
A
