沪科版七年级下册数学 10.2 平行线的判定 课件 (共23张PPT)
文档属性
| 名称 | 沪科版七年级下册数学 10.2 平行线的判定 课件 (共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-15 10:51:35 | ||
图片预览



文档简介
(共23张PPT)
10.2
平行线的判定
第2课时
平行线的判定方法
第10章
相交线、平行线与平移
温故而知新:
【三线八角】
*同位角
*内错角
*同旁内角
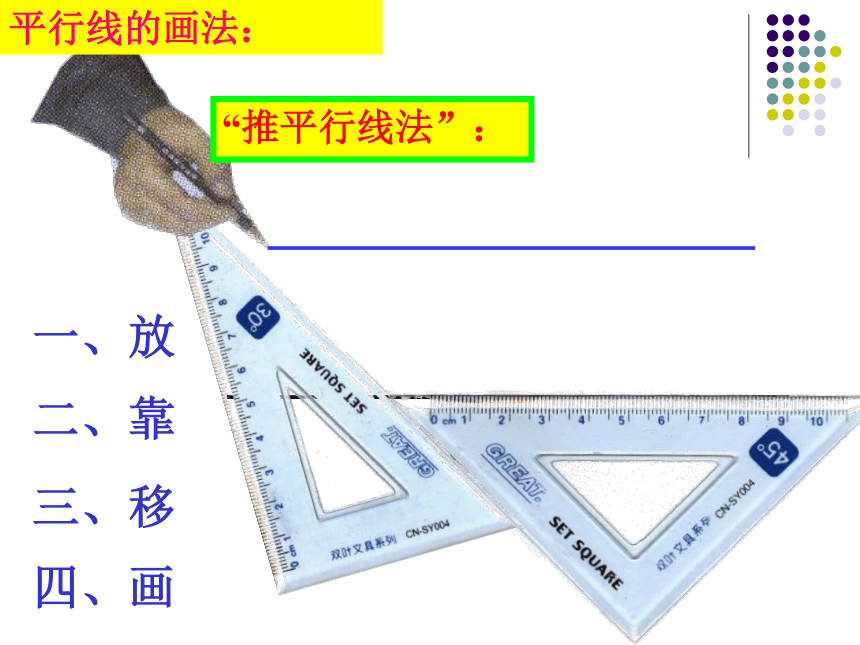
一、放
二、靠
三、移
四、画
平行线的画法:
“推平行线法”:
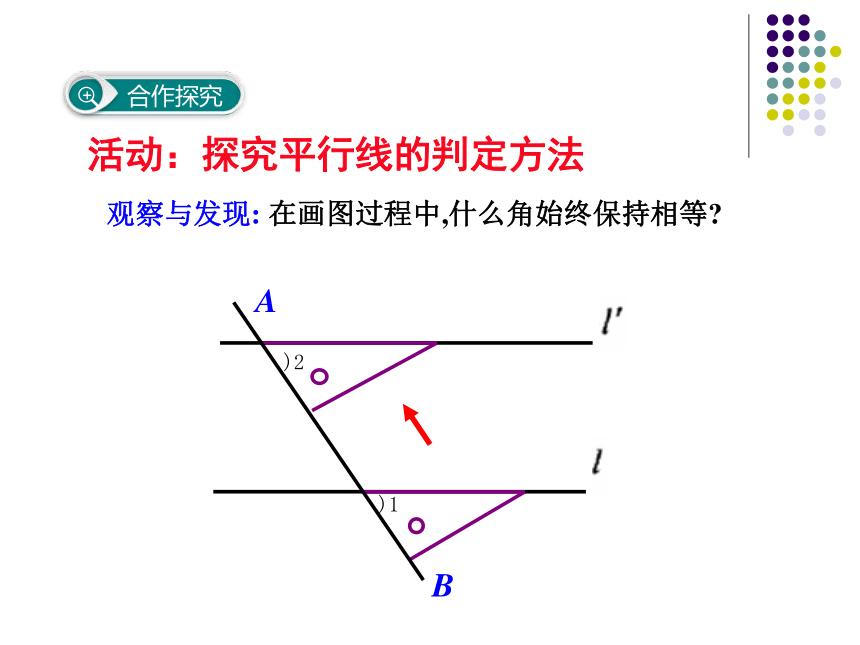
观察与发现:
在画图过程中,什么角始终保持相等?
活动:探究平行线的判定方法
A
B
)2
)1
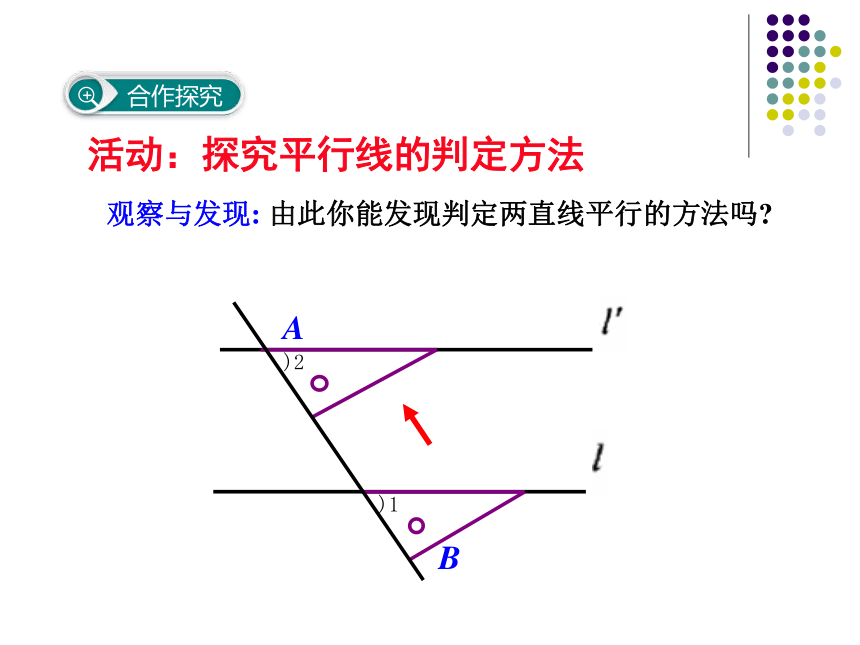
观察与发现:
由此你能发现判定两直线平行的方法吗?
活动:探究平行线的判定方法
A
B
)2
)1
一般地,判断两直线平行有下面的方法:
判定方法1
两条直线被第三条直线所截
,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
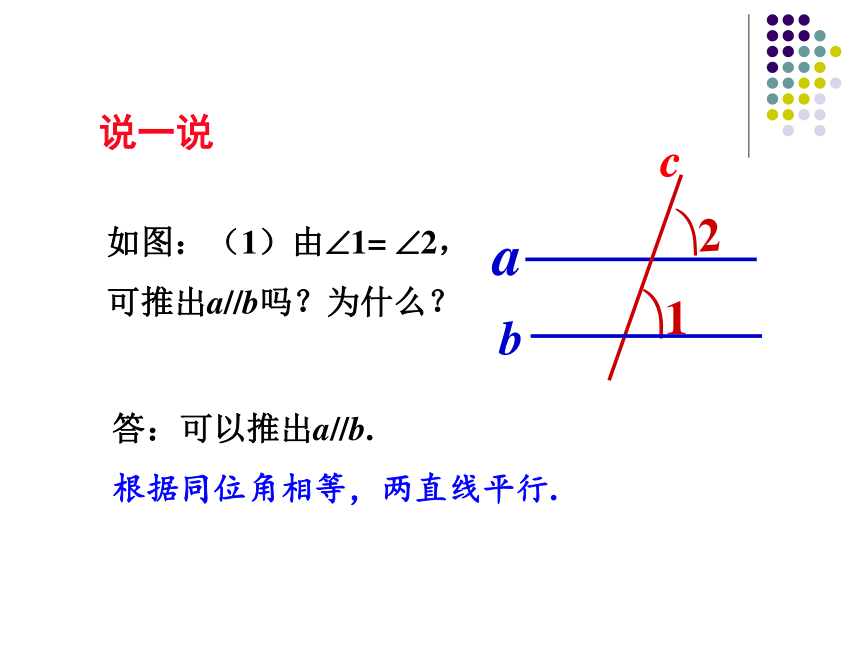
如图:(1)由?1=
?2,
可推出a//b吗?为什么?
说一说
答:可以推出a//b.
根据同位角相等,两直线平行.
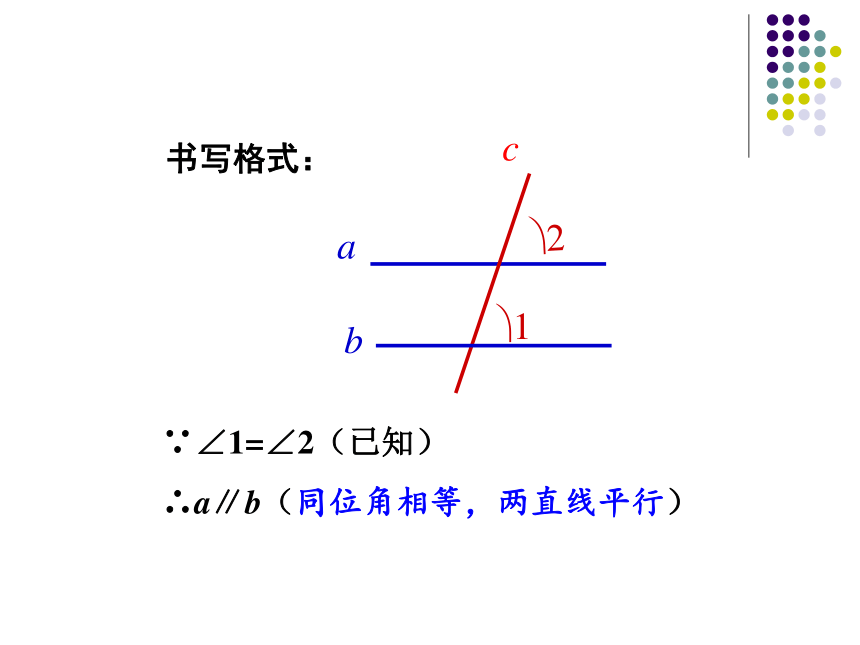
∵∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
书写格式:
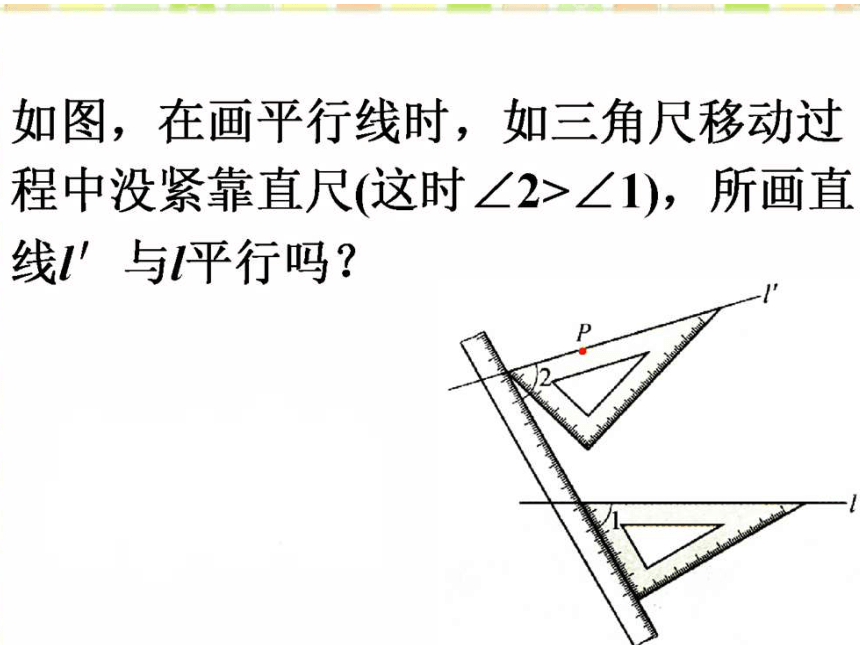
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角,或同旁内角来判定两直线平行呢?
思考:
由?3=
?2,可推出a//b吗?如何推出?
写出你的推理过程.
解:∵
?3=?2(已知)
又∵?3=
?1(对顶角相等)
?
?1=
?2(等量代换)
?
a//b(同位角相等,两直线平行)
2
c
b
a
3
思考1
1
判定方法2
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
一般地,判断两直线平行有下面的方法:
如图,∠1=
∠2
,且∠1=∠3,
AB和CD平行吗?
想一想
1
如果?1+?2=180°
能判定a//b吗?
c
解:能,
因为?1+?2=180°
?1+?3=180°
所以
?2=?3
所以
a//b
思考2
判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
一般地,判断两直线平行有下面的方法:
如图:?B=
?
D=45°,
?
C=135°,问图中有哪些
直线平行?
答:AB//CD,AD//BC
∵?
B=45°(已知)
?
C=135°(已知)
??
B+
?
C=180°
?
AB//CD(同旁内角互补,两直线平行)
同理:AD//BC
想一想
判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
3
4
文字叙述
符号语言
图形
相等
两直线平行
∵
(已知)
∴a∥b
相等
两直线平行
互补,
两直线平行
∵
(已知)
∴a∥b
∵
∴a∥b
1.
如图,不能判定
的是
(
)
(A)∠2=∠3
(B)∠1=∠4
(C)∠1=∠2
(D)∠1=∠3
D
2.
如图,∠1=∠2,则下列结论正确的是(
)
A.
AD//BC
B.
AB//CD
C.
AD//EF
D.
EF//BC
C
3.如图,哪些直线平行,哪些直线不平行?
4.如图,已知∠1=30°,∠2或
∠3满足条件________________________,则a//b.
∠2=150或∠3=30°
平行线判定方法1:同位角相等,两直线平行。
平行线判定方法2:内错角相等,两直线平行。
平行线判定方法3:同旁内角互补,两直线平行。
学以致用:课后思考题
一辆货车在仓库装满货物准备运往超市,驶出仓库口后开始向东行驶,途中向右拐了50°角,接着向前行驶,走了一段路程后,又向左拐了50°角,如图所示。此时货车和原来的行驶方向相同吗?你的依据是什么?
10.2
平行线的判定
第2课时
平行线的判定方法
第10章
相交线、平行线与平移
温故而知新:
【三线八角】
*同位角
*内错角
*同旁内角
一、放
二、靠
三、移
四、画
平行线的画法:
“推平行线法”:
观察与发现:
在画图过程中,什么角始终保持相等?
活动:探究平行线的判定方法
A
B
)2
)1
观察与发现:
由此你能发现判定两直线平行的方法吗?
活动:探究平行线的判定方法
A
B
)2
)1
一般地,判断两直线平行有下面的方法:
判定方法1
两条直线被第三条直线所截
,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
如图:(1)由?1=
?2,
可推出a//b吗?为什么?
说一说
答:可以推出a//b.
根据同位角相等,两直线平行.
∵∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
书写格式:
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角,或同旁内角来判定两直线平行呢?
思考:
由?3=
?2,可推出a//b吗?如何推出?
写出你的推理过程.
解:∵
?3=?2(已知)
又∵?3=
?1(对顶角相等)
?
?1=
?2(等量代换)
?
a//b(同位角相等,两直线平行)
2
c
b
a
3
思考1
1
判定方法2
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
一般地,判断两直线平行有下面的方法:
如图,∠1=
∠2
,且∠1=∠3,
AB和CD平行吗?
想一想
1
如果?1+?2=180°
能判定a//b吗?
c
解:能,
因为?1+?2=180°
?1+?3=180°
所以
?2=?3
所以
a//b
思考2
判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
一般地,判断两直线平行有下面的方法:
如图:?B=
?
D=45°,
?
C=135°,问图中有哪些
直线平行?
答:AB//CD,AD//BC
∵?
B=45°(已知)
?
C=135°(已知)
??
B+
?
C=180°
?
AB//CD(同旁内角互补,两直线平行)
同理:AD//BC
想一想
判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
3
4
文字叙述
符号语言
图形
相等
两直线平行
∵
(已知)
∴a∥b
相等
两直线平行
互补,
两直线平行
∵
(已知)
∴a∥b
∵
∴a∥b
1.
如图,不能判定
的是
(
)
(A)∠2=∠3
(B)∠1=∠4
(C)∠1=∠2
(D)∠1=∠3
D
2.
如图,∠1=∠2,则下列结论正确的是(
)
A.
AD//BC
B.
AB//CD
C.
AD//EF
D.
EF//BC
C
3.如图,哪些直线平行,哪些直线不平行?
4.如图,已知∠1=30°,∠2或
∠3满足条件________________________,则a//b.
∠2=150或∠3=30°
平行线判定方法1:同位角相等,两直线平行。
平行线判定方法2:内错角相等,两直线平行。
平行线判定方法3:同旁内角互补,两直线平行。
学以致用:课后思考题
一辆货车在仓库装满货物准备运往超市,驶出仓库口后开始向东行驶,途中向右拐了50°角,接着向前行驶,走了一段路程后,又向左拐了50°角,如图所示。此时货车和原来的行驶方向相同吗?你的依据是什么?
