沪科版七年级下册数学:7.2 一元一次不等式及其解法 课件 (共23张PPT)
文档属性
| 名称 | 沪科版七年级下册数学:7.2 一元一次不等式及其解法 课件 (共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 729.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-15 20:29:56 | ||
图片预览






文档简介
(共23张PPT)
7.2
一元一次不等式组
第一课时
创设情境
导入新课
问题
用每分钟抽30t水的抽水机来抽污水管道积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么?
问题
解:设用x分钟将污水抽完,则x满足
30
x
>1200
①
30
x
<1500
②
一元一次不等式组的概念
类似于方程组,把这两个或两个以上含有相同
未知数的一元一次不等式合起来就构成了一元
一次不等式组。
30
x
>1200
①
30
x
<1500
②
下列各式中,哪些是一元一次不等式组?
√
×
×
×
观察与思考
观察与思考
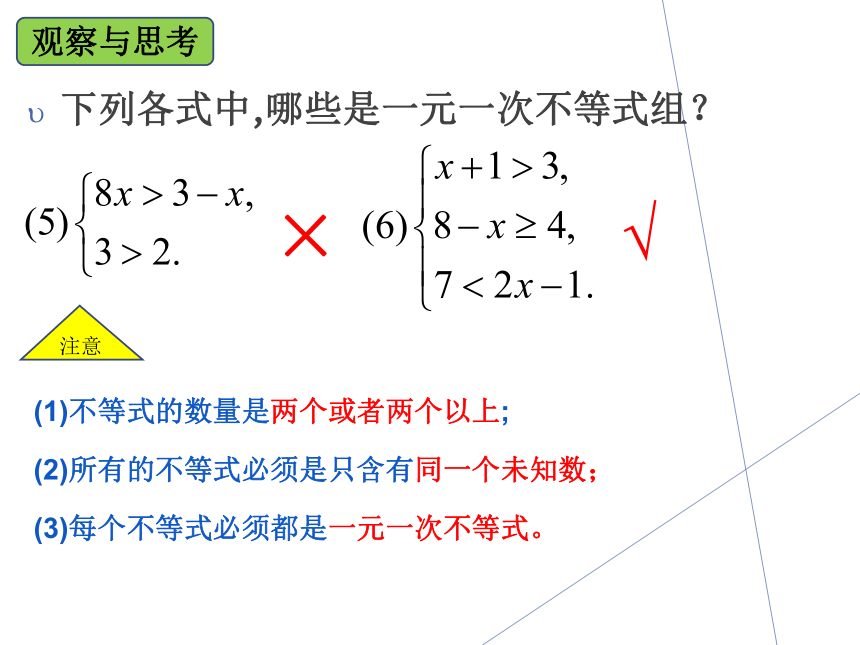
下列各式中,哪些是一元一次不等式组?
×
√
注意
(1)不等式的数量是两个或者两个以上;
(2)所有的不等式必须是只含有同一个未知数;
(3)每个不等式必须都是一元一次不等式。
30
x
>1200
①
30
x
<1500
②
如何确定不等式组中x的取值范围?
不等式组中的各个不等式解集的公共部分,
就是不等式组的解集.
引导归纳
得出结论
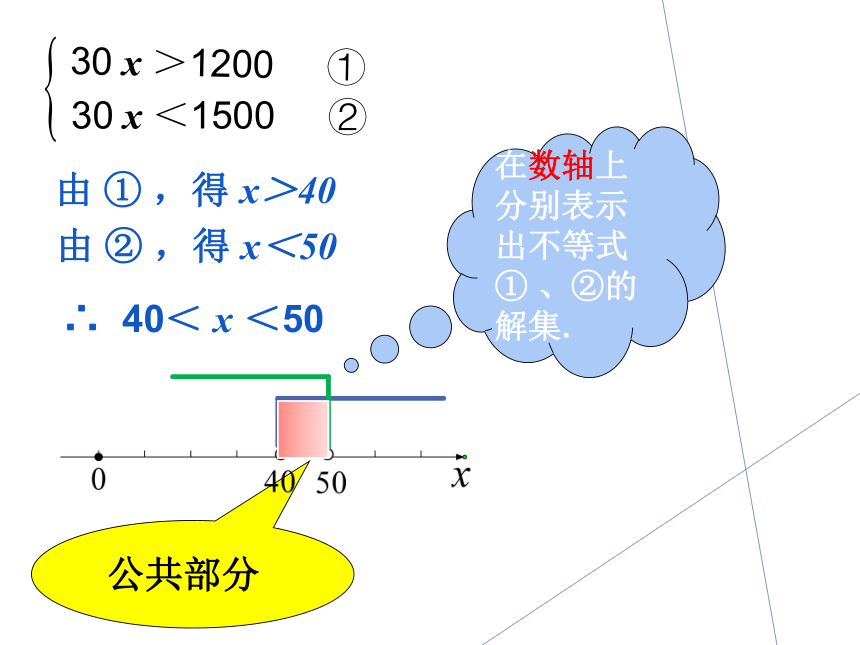
由
①
,得
x>40
由
②
,得
x<50
在数轴上分别表示出不等式①
、②的解集.
30
x
>1200
①
30
x
<1500
②
∴
40<
x
<50
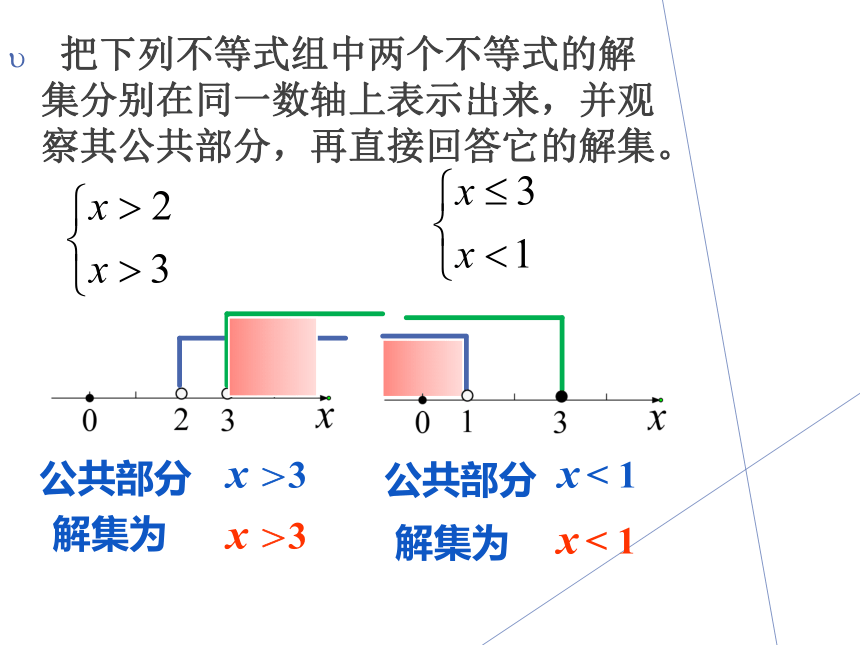
把下列不等式组中两个不等式的解集分别在同一数轴上表示出来,并观察其公共部分,再直接回答它的解集。
你会找公共部分吗?
求下列不等式组的解集:(第一小组)
求下列不等式组的解集:(第二小组)
求下列不等式组的解集:(第三小组)
求下列不等式组的解集:(第四小组)
解:原不等式组无解.
解:原不等式组无解.
a
a
a
b
x
<
a
x
>
b
。
。
a
。
。
b
。
。
b
。
。
b
解集为
:
x
>
b
解集为
:
x
<
a
(a<
b
)
解集为:
a
<
x
<
b
解集为:无解
一元一次不等式组解集的图形规律
同大取大,同小取小,一大一小取中间,中间没有就无解.
应用新知
尝试练习
例1.解下列不等式组
解:
由①得
x
>
2
由②得
x
>
3
∴
x
>
3
由①得
x
≥
8
由②得
x
<
0.8
∴
原不等式组无解
练习:解下列不等式
发散思维
巩固提升
例2.x取哪些整数值时,不等式
都成立?
解:
由①得
x
>
-2.5
由②得
x
≤
4
∴
-2.5≤
4
解不等式组
∴
x可取的整数值为-2,-1,0,1,2,3,4.
练习:已知不等式组
无解,
求a的取值范围.
由①得
x
>
3
由②得
x
<
a-1
∵
原不等式无解
∴
a-1≤3
即
a≤4
归纳总结
布置作业
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的
公共部分;
(3)根据几个不等式解集的公共部分,
写出这个不等式组的解集.
通过这节课的学习,你认为解一元一次不等
式组的一般步骤是什么?
议一议
同大取大,同小取小,一大一小取中间,中间没有就无解.
知识小结
2.一元一次不等式组的解集
3.解一元一次不等式组的一般步骤
1.一元一次不等式组的概念
数学思想
课本第130页习题2,3,4
布置作业
7.2
一元一次不等式组
第一课时
创设情境
导入新课
问题
用每分钟抽30t水的抽水机来抽污水管道积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么?
问题
解:设用x分钟将污水抽完,则x满足
30
x
>1200
①
30
x
<1500
②
一元一次不等式组的概念
类似于方程组,把这两个或两个以上含有相同
未知数的一元一次不等式合起来就构成了一元
一次不等式组。
30
x
>1200
①
30
x
<1500
②
下列各式中,哪些是一元一次不等式组?
√
×
×
×
观察与思考
观察与思考
下列各式中,哪些是一元一次不等式组?
×
√
注意
(1)不等式的数量是两个或者两个以上;
(2)所有的不等式必须是只含有同一个未知数;
(3)每个不等式必须都是一元一次不等式。
30
x
>1200
①
30
x
<1500
②
如何确定不等式组中x的取值范围?
不等式组中的各个不等式解集的公共部分,
就是不等式组的解集.
引导归纳
得出结论
由
①
,得
x>40
由
②
,得
x<50
在数轴上分别表示出不等式①
、②的解集.
30
x
>1200
①
30
x
<1500
②
∴
40<
x
<50
把下列不等式组中两个不等式的解集分别在同一数轴上表示出来,并观察其公共部分,再直接回答它的解集。
你会找公共部分吗?
求下列不等式组的解集:(第一小组)
求下列不等式组的解集:(第二小组)
求下列不等式组的解集:(第三小组)
求下列不等式组的解集:(第四小组)
解:原不等式组无解.
解:原不等式组无解.
a
a
a
b
x
<
a
x
>
b
。
。
a
。
。
b
。
。
b
。
。
b
解集为
:
x
>
b
解集为
:
x
<
a
(a<
b
)
解集为:
a
<
x
<
b
解集为:无解
一元一次不等式组解集的图形规律
同大取大,同小取小,一大一小取中间,中间没有就无解.
应用新知
尝试练习
例1.解下列不等式组
解:
由①得
x
>
2
由②得
x
>
3
∴
x
>
3
由①得
x
≥
8
由②得
x
<
0.8
∴
原不等式组无解
练习:解下列不等式
发散思维
巩固提升
例2.x取哪些整数值时,不等式
都成立?
解:
由①得
x
>
-2.5
由②得
x
≤
4
∴
-2.5
4
解不等式组
∴
x可取的整数值为-2,-1,0,1,2,3,4.
练习:已知不等式组
无解,
求a的取值范围.
由①得
x
>
3
由②得
x
<
a-1
∵
原不等式无解
∴
a-1≤3
即
a≤4
归纳总结
布置作业
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的
公共部分;
(3)根据几个不等式解集的公共部分,
写出这个不等式组的解集.
通过这节课的学习,你认为解一元一次不等
式组的一般步骤是什么?
议一议
同大取大,同小取小,一大一小取中间,中间没有就无解.
知识小结
2.一元一次不等式组的解集
3.解一元一次不等式组的一般步骤
1.一元一次不等式组的概念
数学思想
课本第130页习题2,3,4
布置作业
