7.3多边形的内角和习题课
文档属性
| 名称 | 7.3多边形的内角和习题课 |  | |
| 格式 | rar | ||
| 文件大小 | 137.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-11 18:06:12 | ||
图片预览




文档简介
(共24张PPT)
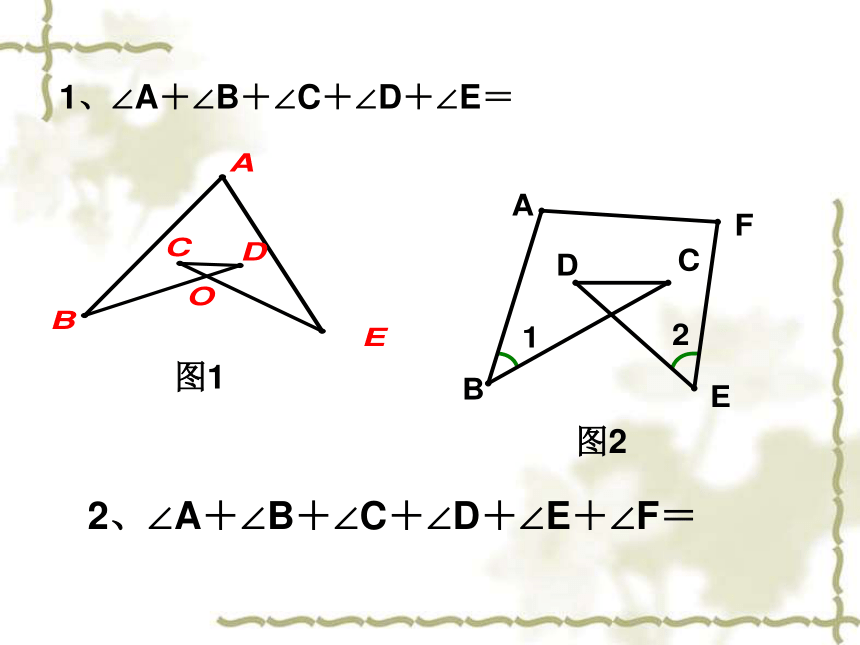
1、∠A+∠B+∠C+∠D+∠E=
2、∠A+∠B+∠C+∠D+∠E+∠F=
图1
图2
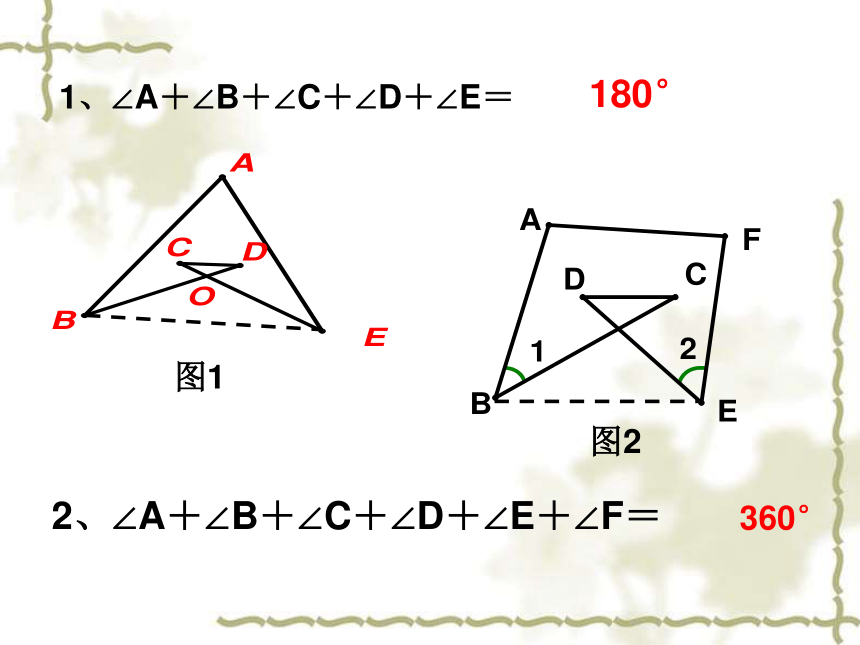
1、∠A+∠B+∠C+∠D+∠E=
2、∠A+∠B+∠C+∠D+∠E+∠F=
图1
图2
180°
360°
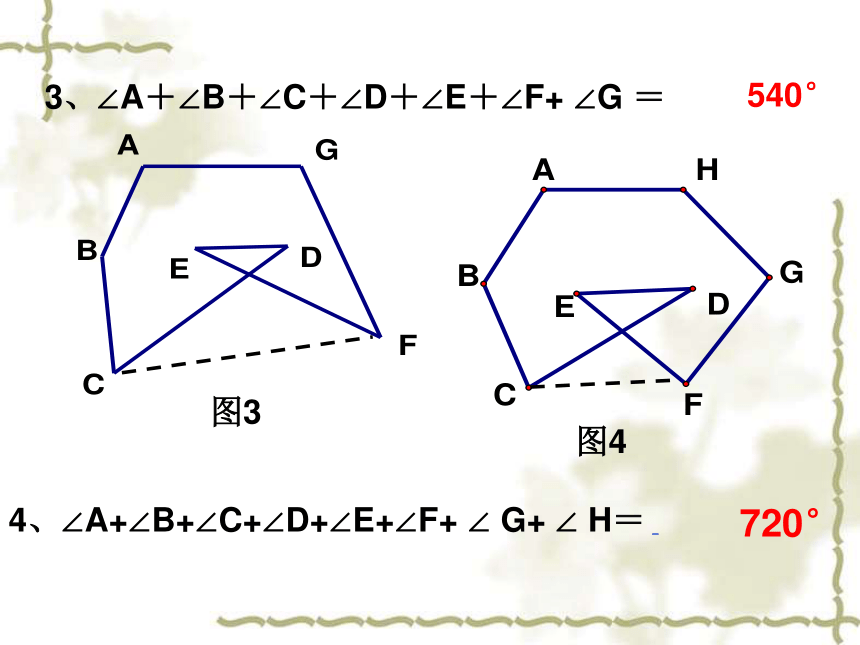
3、∠A+∠B+∠C+∠D+∠E+∠F+ ∠G =
4、∠A+∠B+∠C+∠D+∠E+∠F+ ∠ G+ ∠ H=
图3
图4
540°
720°
学习目标:
1、能够进一步理解多边形、正多边形的定义,以及多边形的边、内角、外角、对角线等有关内容;
2、会运用多边形的内角和与外角和定理进行有关推理、计算,进一步发展合情推理意识和推理能力;
3、体会方程思想和转化思想以及分类讨论方法在解决多边形问题中的应用,从而提高分析问题和解决问题的能力。
学习重点:
多边形内角和与外角和定理及其应用。
学习难点:
多边形内角和与外角和的综合应用。
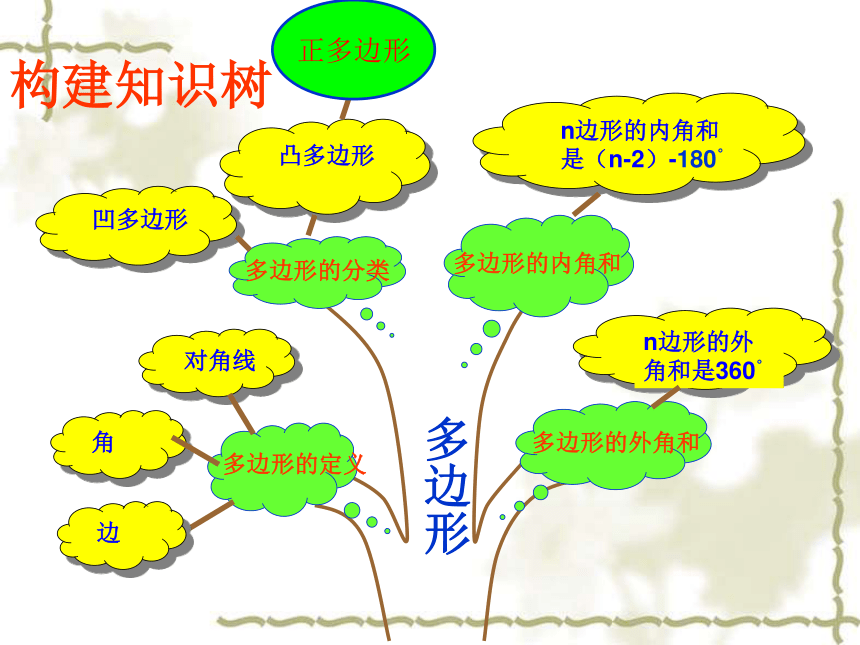
构建知识树
多边形的定义
角
n边形的内角和是(n-2)-180°
对角线
凹多边形
凸多边形
n边形的外角和是360°
正多边形
多边形
边
多边形的分类
多边形的内角和
多边形的外角和
活动1、基础知识过关:
1、过n边形的一个顶点,可以画__________条对角线,这些对角线将这个多边形分成了_______个三角形;
2、n边形中一共可以画______________条对角线;
3、多边形的内角和公式 ;多边形的外角和是 ;
4、多边形的一个外角和它相邻的内角的关系: ;
5、正n边形的每一个内角的度数: ;
6、正n边形的每一个外角的度数: ;
7、平面内, , 的多边形是正多边形 (两个条件缺一不可)。
(n-3)
(n-2)
(n-2) ·180°
360°
互为邻补角
(n-2) ·180°÷n
360°÷n
各条边都相等
各个角都相等
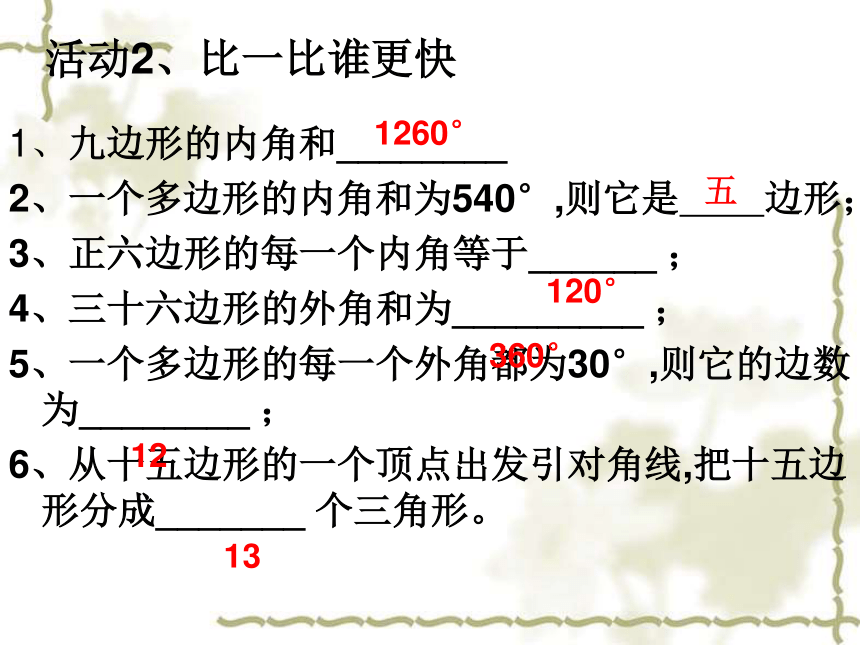
活动2、比一比谁更快
1、九边形的内角和________
2、一个多边形的内角和为540°,则它是 边形;
3、正六边形的每一个内角等于______ ;
4、三十六边形的外角和为_________ ;
5、一个多边形的每一个外角都为30°,则它的边数为________ ;
6、从十五边形的一个顶点出发引对角线,把十五边形分成_______ 个三角形。
1260°
五
120°
360°
12
13
活动3:综合应用
1、一个多边形的内角和比它的外角和多720°,并且这个多边形的各内角都相等,
求这个多边形的每个内角等于多少度?
解:设这个多边形的边数为n,那么这个多边形的内角和为(n-2)*180°.
根据题意列方程得:
(n-2)*180°=360°+720°
解得:n=8
(8-2)×180°÷8=6×180°÷8
=1080°÷8=135°
答:这个多边形是八边形,每个内角都等于135°。
2、一个长方形截掉一个角后,得到一个多边形,这个多边形的内角和是多少度?
活动4:奇思妙想
思路分析:得到的多边形是几边形呢?会有几种不同的情况?
解:长方形去掉一个角后得到的多边形有3种情况,如图:
它们分别是三角形、四边形、五边形,所以内角和分别为180°、360°、540°
3、一个多边形除了一个内角以后,其余各角的和为2750°,
求这个多边形的边数及这个内角的度数。
活动5:思维提升
解:设这个多边形的边数为n,这个内角的度数为x,根据题意列方程得:
方程变形为:(n-2)×180°=2750°+x
因为方程左边是是180°的整数倍,所以方程右边 2750°+x 也是180°的整数倍。
由 2750°+ x = + x,
解得:x=130°,n=18.
答:这个多边形的边数为18,这个内角的度数为130°。
(n-2)×180°-x=2750°
180°×15 + 50°
因为0°﹤x﹤180°所以 50°+ x=180°,
4、如图(1)是一个五角星ABCDE,你能计算出∠A+∠B+∠C+∠D+∠E=
活动6:巧题妙解
图1
O
180°
计算各图中∠A+∠B+∠C+∠D+∠E=
180°
活动4、课堂检测
1、若一个多边形的外角和等于它内角和的2倍,则这个多边形是( )
A 三角形 B 四边形 C 五边形 D 以上答案都不对
2、一个多边形的内角和是720°,则这个多边形的对角线的条数为( )
A 7 B 8 C 9 D 10
3、多边形的边数每增加一条其内角和增加( )
A 90° B 180° C 360° D 不能确定
4、正多边形的外角不可能等于( )
A 20° B 30° C 40° D 50°
A
C
B
D
5、一个多边形的内角中锐角的个数最多有( )
A 3个 B 4个 C 5个 D 6个
6、如图,小亮从点A出发前进10m,向右转15°,再向前进10m,有向右转15°,这样一直下去,他第一次回到出发点A时,一共走了 m 。
A
A
15°
15°
15°
240
7、如图:∠A+∠B+∠C+∠D+∠E+∠F= .
A
D
E
C
F
B
N
P
M
360°
通过这节课的学习同学们有哪些收获?
有一个家庭联谊会,参加的家庭全部是三口之家,在联谊会期间,每个人都要和别的家庭的每个成员握一次手。
(1)若参加会议的人数为15,每一个人要握手多少次?
(2)若参加会议的人数为15,这些人一共要握手多少次?
谢谢!
一个多边形中,除去其中一个内角以后,其它内角的和为1205°,
求这个多边形的边数及其内角和是多少?
活动3:学以致用 巩固练习
解:设这个多边形的边数为n,这个内角的度数为x,
根据题意列方程得:
(n-2)×180°-x= 1205°
方程变形为:(n-2)×180°=1205°+x
由题意可知: 1205°+x 是180°的整数倍,且0°﹤x﹤180°;
由1205°+ x =180°×8+125°+ x,所以125°+ x=180°,
解得:x=55°,n=9。
(9-2)× 180°=1260°
答:这个多边形的边数为9,这个多边形的内角和为1260°。
活动3:学以致用 变式练习:
多边形的一个外角与其内角和的度数总和为600°,求这个多边形的边数及这个外角的度数分别是多少?
解:设这个多边形的边数为n,这个外角的度数为x,根据题意列方程得:
(n-2)×180°+x=600°
方程变形为:(n-2)×180°=600°-x
由题意可知: 600°- x 是180°的整数倍,且0°﹤x﹤180°;
由600°- x =180°×3 + 60°- x,所以60°- x=0,
解得:x=60°,n=5.
答:这个多边形的边数为5,这个外角的度数为60°。
活动2:综合应用
例2、(2)如果一个多边形被截掉一个角后,得到的多边形的内角和是360°,原多边形的边数是多少?
思路分析:得到的多边形的内角和是360°,即多边形的边数是多少?能有几种情况得到
解:原多边形有3种情况:如图
原多边形是三角形、或四边形、或五边形。
1、∠A+∠B+∠C+∠D+∠E=
2、∠A+∠B+∠C+∠D+∠E+∠F=
图1
图2
1、∠A+∠B+∠C+∠D+∠E=
2、∠A+∠B+∠C+∠D+∠E+∠F=
图1
图2
180°
360°
3、∠A+∠B+∠C+∠D+∠E+∠F+ ∠G =
4、∠A+∠B+∠C+∠D+∠E+∠F+ ∠ G+ ∠ H=
图3
图4
540°
720°
学习目标:
1、能够进一步理解多边形、正多边形的定义,以及多边形的边、内角、外角、对角线等有关内容;
2、会运用多边形的内角和与外角和定理进行有关推理、计算,进一步发展合情推理意识和推理能力;
3、体会方程思想和转化思想以及分类讨论方法在解决多边形问题中的应用,从而提高分析问题和解决问题的能力。
学习重点:
多边形内角和与外角和定理及其应用。
学习难点:
多边形内角和与外角和的综合应用。
构建知识树
多边形的定义
角
n边形的内角和是(n-2)-180°
对角线
凹多边形
凸多边形
n边形的外角和是360°
正多边形
多边形
边
多边形的分类
多边形的内角和
多边形的外角和
活动1、基础知识过关:
1、过n边形的一个顶点,可以画__________条对角线,这些对角线将这个多边形分成了_______个三角形;
2、n边形中一共可以画______________条对角线;
3、多边形的内角和公式 ;多边形的外角和是 ;
4、多边形的一个外角和它相邻的内角的关系: ;
5、正n边形的每一个内角的度数: ;
6、正n边形的每一个外角的度数: ;
7、平面内, , 的多边形是正多边形 (两个条件缺一不可)。
(n-3)
(n-2)
(n-2) ·180°
360°
互为邻补角
(n-2) ·180°÷n
360°÷n
各条边都相等
各个角都相等
活动2、比一比谁更快
1、九边形的内角和________
2、一个多边形的内角和为540°,则它是 边形;
3、正六边形的每一个内角等于______ ;
4、三十六边形的外角和为_________ ;
5、一个多边形的每一个外角都为30°,则它的边数为________ ;
6、从十五边形的一个顶点出发引对角线,把十五边形分成_______ 个三角形。
1260°
五
120°
360°
12
13
活动3:综合应用
1、一个多边形的内角和比它的外角和多720°,并且这个多边形的各内角都相等,
求这个多边形的每个内角等于多少度?
解:设这个多边形的边数为n,那么这个多边形的内角和为(n-2)*180°.
根据题意列方程得:
(n-2)*180°=360°+720°
解得:n=8
(8-2)×180°÷8=6×180°÷8
=1080°÷8=135°
答:这个多边形是八边形,每个内角都等于135°。
2、一个长方形截掉一个角后,得到一个多边形,这个多边形的内角和是多少度?
活动4:奇思妙想
思路分析:得到的多边形是几边形呢?会有几种不同的情况?
解:长方形去掉一个角后得到的多边形有3种情况,如图:
它们分别是三角形、四边形、五边形,所以内角和分别为180°、360°、540°
3、一个多边形除了一个内角以后,其余各角的和为2750°,
求这个多边形的边数及这个内角的度数。
活动5:思维提升
解:设这个多边形的边数为n,这个内角的度数为x,根据题意列方程得:
方程变形为:(n-2)×180°=2750°+x
因为方程左边是是180°的整数倍,所以方程右边 2750°+x 也是180°的整数倍。
由 2750°+ x = + x,
解得:x=130°,n=18.
答:这个多边形的边数为18,这个内角的度数为130°。
(n-2)×180°-x=2750°
180°×15 + 50°
因为0°﹤x﹤180°所以 50°+ x=180°,
4、如图(1)是一个五角星ABCDE,你能计算出∠A+∠B+∠C+∠D+∠E=
活动6:巧题妙解
图1
O
180°
计算各图中∠A+∠B+∠C+∠D+∠E=
180°
活动4、课堂检测
1、若一个多边形的外角和等于它内角和的2倍,则这个多边形是( )
A 三角形 B 四边形 C 五边形 D 以上答案都不对
2、一个多边形的内角和是720°,则这个多边形的对角线的条数为( )
A 7 B 8 C 9 D 10
3、多边形的边数每增加一条其内角和增加( )
A 90° B 180° C 360° D 不能确定
4、正多边形的外角不可能等于( )
A 20° B 30° C 40° D 50°
A
C
B
D
5、一个多边形的内角中锐角的个数最多有( )
A 3个 B 4个 C 5个 D 6个
6、如图,小亮从点A出发前进10m,向右转15°,再向前进10m,有向右转15°,这样一直下去,他第一次回到出发点A时,一共走了 m 。
A
A
15°
15°
15°
240
7、如图:∠A+∠B+∠C+∠D+∠E+∠F= .
A
D
E
C
F
B
N
P
M
360°
通过这节课的学习同学们有哪些收获?
有一个家庭联谊会,参加的家庭全部是三口之家,在联谊会期间,每个人都要和别的家庭的每个成员握一次手。
(1)若参加会议的人数为15,每一个人要握手多少次?
(2)若参加会议的人数为15,这些人一共要握手多少次?
谢谢!
一个多边形中,除去其中一个内角以后,其它内角的和为1205°,
求这个多边形的边数及其内角和是多少?
活动3:学以致用 巩固练习
解:设这个多边形的边数为n,这个内角的度数为x,
根据题意列方程得:
(n-2)×180°-x= 1205°
方程变形为:(n-2)×180°=1205°+x
由题意可知: 1205°+x 是180°的整数倍,且0°﹤x﹤180°;
由1205°+ x =180°×8+125°+ x,所以125°+ x=180°,
解得:x=55°,n=9。
(9-2)× 180°=1260°
答:这个多边形的边数为9,这个多边形的内角和为1260°。
活动3:学以致用 变式练习:
多边形的一个外角与其内角和的度数总和为600°,求这个多边形的边数及这个外角的度数分别是多少?
解:设这个多边形的边数为n,这个外角的度数为x,根据题意列方程得:
(n-2)×180°+x=600°
方程变形为:(n-2)×180°=600°-x
由题意可知: 600°- x 是180°的整数倍,且0°﹤x﹤180°;
由600°- x =180°×3 + 60°- x,所以60°- x=0,
解得:x=60°,n=5.
答:这个多边形的边数为5,这个外角的度数为60°。
活动2:综合应用
例2、(2)如果一个多边形被截掉一个角后,得到的多边形的内角和是360°,原多边形的边数是多少?
思路分析:得到的多边形的内角和是360°,即多边形的边数是多少?能有几种情况得到
解:原多边形有3种情况:如图
原多边形是三角形、或四边形、或五边形。
