人教版高中选修3-3物理7.1物体是由大量分子组成的(32张PPT)
文档属性
| 名称 | 人教版高中选修3-3物理7.1物体是由大量分子组成的(32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 911.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-16 08:48:50 | ||
图片预览








文档简介
(共32张PPT)
第七章
分子热运动
7.1
物体是由大量分子组成的
学习目标
1.知道可以用单分子油膜法测定分子直径.
2.知道阿伏加德罗常数的含义,并记住
这个常数的数值和单位.
3.知道一般分子的直径和质量的数量级.
4.会用阿伏加德罗常数、摩尔质量、摩尔
体积,估算分子大小或根据分子大小估算阿伏加德罗常数.
引入:
初中学过的有关分子运动的中,我们已知道物体是由大量分子组成的.
在热学中由于原子、离子、或分子做热运动时遵从相同的规律,所以统称为分子.
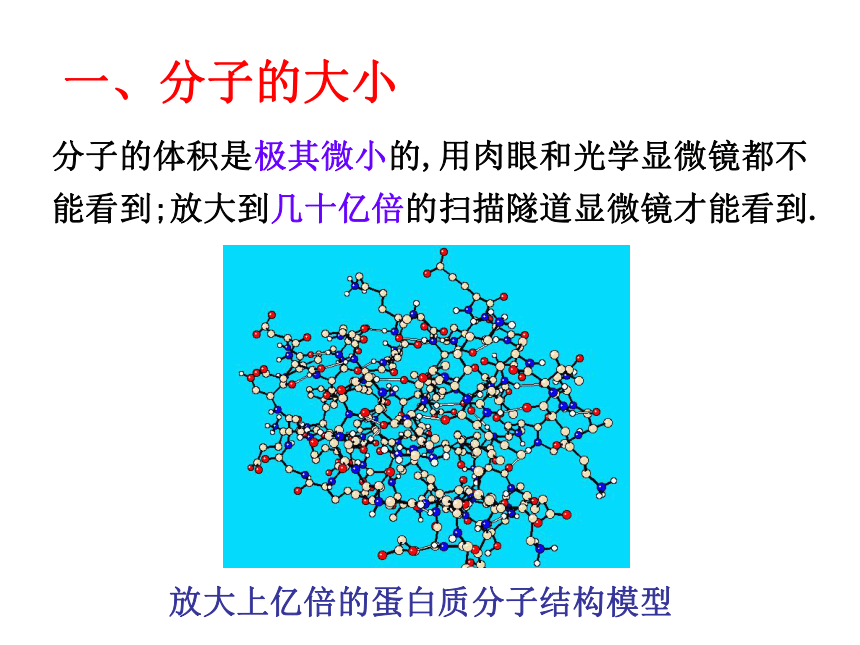
一、分子的大小
放大上亿倍的蛋白质分子结构模型
分子的体积是极其微小的,用肉眼和光学显微镜都不能看到;放大到几十亿倍的扫描隧道显微镜才能看到.
请阅读课文P69最下面一段
怎样才能知道分子的大小呢?
2.具体做法是:
将一滴体积已知的小油滴,
滴在水面上,
在重力作用下尽可能的散开形成一层极薄的油膜,
此时油膜可看成单分子油膜,油膜的厚度看成是油酸分子的直径,
所以只要再测定出这层油膜的面积,
就可求出油分子直径的大小.
1.有一种粗略测定分子大小的方法叫油膜法.
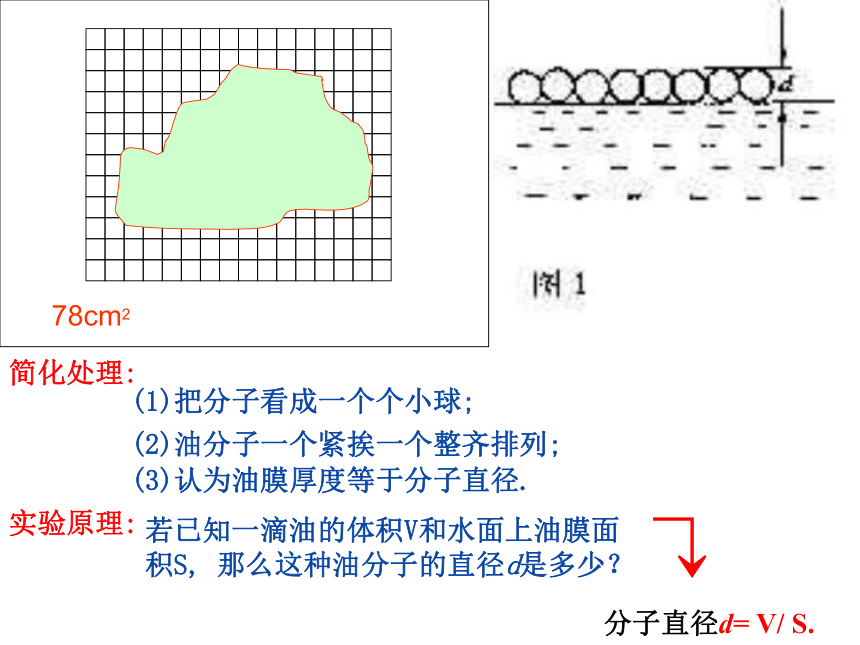
78cm2
实验原理:
若已知一滴油的体积V和水面上油膜面
积S,
那么这种油分子的直径d是多少?
分子直径d=
V/
S.
简化处理:
(1)把分子看成一个个小球;
(2)油分子一个紧挨一个整齐排列;
(3)认为油膜厚度等于分子直径.
?
(3)数量级:
一些数据太大或很小,为了书写方便,习惯上用科学记数法写成10的乘方数,如
3×10-10m。我们把10的乘方数叫做数量级,
1×10-10m和
9×10-10m,数量级都是
10-10m。
分子直径数量级:
除少数有机物大分子,一般分子直径的数量级是10-10m。
例:水分子直径是4×10-10m,
氢分子直径是2.3×10-10m
,
钨原子直径是2×10-10m.
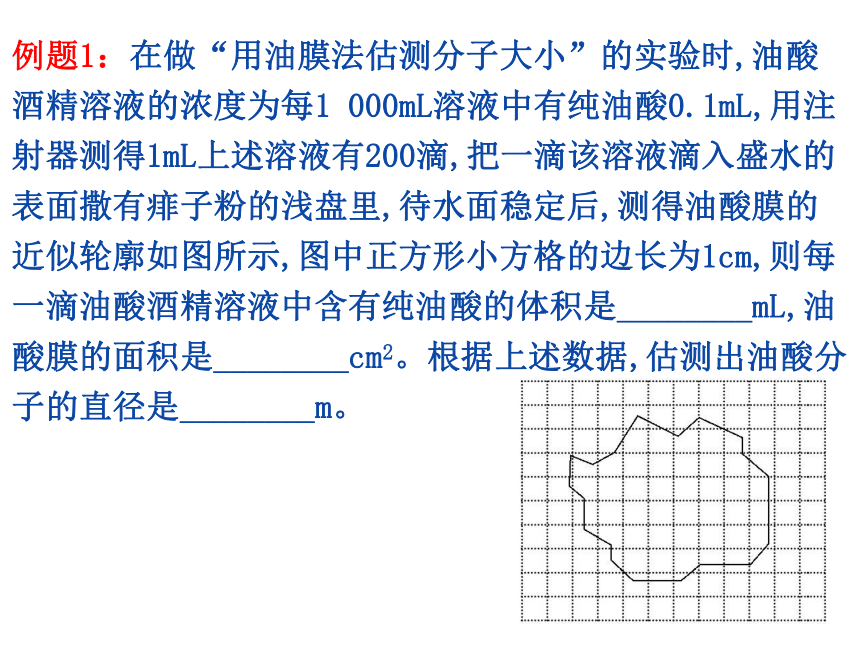
例题1:在做“用油膜法估测分子大小”的实验时,油酸酒精溶液的浓度为每1
000mL溶液中有纯油酸0.1mL,用注射器测得1mL上述溶液有200滴,把一滴该溶液滴入盛水的表面撒有痱子粉的浅盘里,待水面稳定后,测得油酸膜的近似轮廓如图所示,图中正方形小方格的边长为1cm,则每一滴油酸酒精溶液中含有纯油酸的体积是________mL,油酸膜的面积是________cm2。根据上述数据,估测出油酸分子的直径是________m。
解析:每一滴油酸酒精溶液中含有纯油酸的体积为
V=
mL
=
5×10-7mL
油膜的面积S=40×1cm2=40cm2,
分子直径d=
m=1.25×10-10m。
答案:(1)C (2)5×10-7 40 1.25×10-10
【规律方法】油膜法估测分子直径问题的解答技巧
油膜法估测分子直径分三个过程:
(1)获得一滴油酸酒精溶液,并由配制浓度求出其中所含纯油酸的体积V。
(2)用数格子法(不足半个的舍去,多于半个的算一个,即“四舍五入”法)求出油膜面积S。
(3)由公式d=
计算结果。其中V和S的单位均采用国际单位制中的单位,即体积V的单位是m3,面积S的单位是m2。
【过关训练】
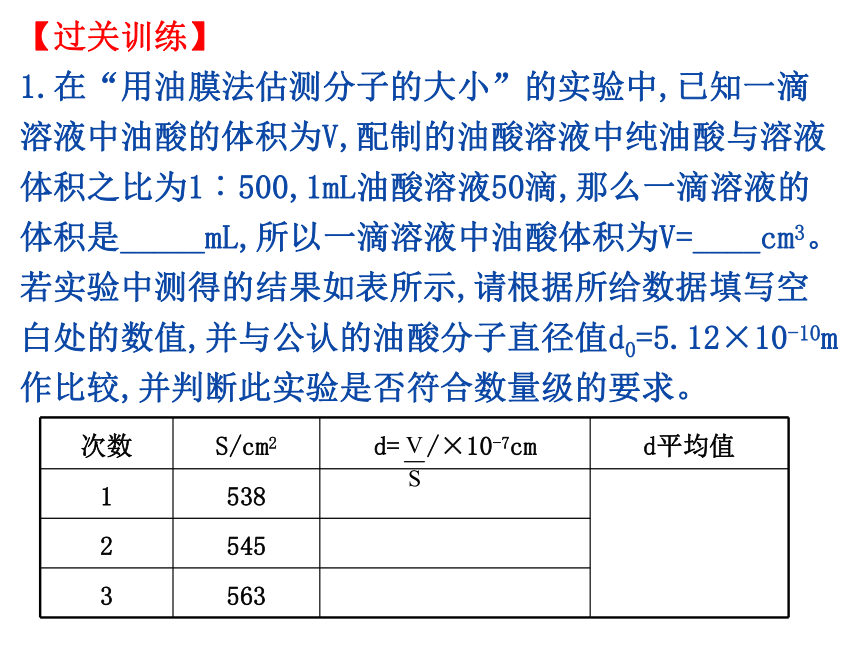
1.在“用油膜法估测分子的大小”的实验中,已知一滴溶液中油酸的体积为V,配制的油酸溶液中纯油酸与溶液体积之比为1︰500,1mL油酸溶液50滴,那么一滴溶液的体积是_____mL,所以一滴溶液中油酸体积为V=____cm3。
若实验中测得的结果如表所示,请根据所给数据填写空白处的数值,并与公认的油酸分子直径值d0=5.12×10-10m作比较,并判断此实验是否符合数量级的要求。
次数
S/cm2
d=
/×10-7cm
d平均值
1
538
2
545
3
563
【解析】1滴溶液的体积V溶液=
mL,
其中含油酸体积
V=
V溶液=4×10-5cm3,
据此算出3次测得的d值分别为
d1≈7.43×10-8cm,d2≈7.34×10-8cm,
d3≈7.10×10-8cm,其平均值
=7.29×10-8cm=7.29×10-10m,
这与公认值的数量级相吻合,故本次估测数值符合数量级的要求。
答案:
4×10-5
0.743
0.734
0.710 7.29×10-10m
符合
【典例示范】在“用单分子油膜估测单分子的大小”的实验中,按照酒精与油酸体积比为m︰n配制油酸酒精溶液,现用滴管滴取油酸酒精溶液,
N滴溶液的总体积为V。
(1)用滴管将一滴油酸酒精溶液滴入浅盘,待稳定后将油酸薄膜轮廓描绘在坐标纸上,如图所示。已知坐标纸上每个小方格面积为S,则油膜面积为_______。
(2)估算油酸分子直径的表达式为
________(用题目中物理量的字母表示)。
【正确解答】(1)根据坐标纸上油酸薄膜的轮廓,数出轮廓范围内正方形的个数为115(不足半个的舍去,多于半个的算一个),又因为坐标纸上每个方格面积为S,则油膜面积为S0=115S。
(2)设油酸的体积为V酸,油酸酒精溶液的浓度为
1滴油酸酒精溶液的体积V滴=
1滴油酸酒精溶液中纯油酸的体积为V0=
则估算油酸分子直径的表达式为d=
答案:(1)115S (2)
二、阿伏加德罗常数
1.阿伏加德罗常数NA:1摩尔(mol)任何物质所含的微粒数叫做阿伏加德罗常数.
2.阿伏加德罗常数是联系微观世界和宏观世界的桥梁.
(1)已知物质的摩尔质量MA,可求出分子质量m0
(其中,VA为摩尔体积,?为物质的密度)
(2)已知物质的量(摩尔数)n,可求出物体所含分子的数目N.
3.有关计算:
(3)已知物质的摩尔体积VA
,可求出分子的体积
V0
4.分子的简化模型:
实际分子的结构是很复杂的,且形状各异。但如果我们只关心分子的大小,而不涉及分子内部的结构和运动时,既可以把分子看成球形,也可以看成立方体。具体分析如下:
(1)对于固体和液体,可认为分子紧密排列,分子间没有空隙,则VA=NAV0(V0为一个分子的体积,VA为摩尔体积)。
①球形分子模型:如图所示,则直径d=
②立方体分子模型:认为每个分子占据一个相同的立方体空间,该立方体的边长即为分子间的平均距离,边长
d=
。如图所示。
(2)对于气体来说,由于气体分子间的距离远大于气体分子的直径,故通过立方体分子模型(不采用球形分子模型),可以估算得到每个气体分子平均占有的空间,而无法得到每个气体分子的实际体积。设每个气体分子占据的空间可看成一个边长为d、体积为V的正方体。气体分子间距离l=d=
,如图所示。(图中黑点代表气体分子所在的位置)
5.总结
阿伏加德罗常数的应用:
(1)微观量:分子质量m0,分子体积V0,分子直径d。
(2)宏观量:物质的质量M、体积V、密度ρ、摩尔质量MA、摩尔体积VA。
(3)微观量与宏观量的关系。
①分子质量:m0=
②分子体积:
(适用于固体和液体)。
③物质所含的分子数:
④阿伏加德罗常数:
(只适用于固体、液体)。
⑤气体分子间的平均距离:
(V0为气体分子所占据空间的体积)。
⑥固体、液体分子直径:
(V0为分子体积)。
【特别提醒】
(1)分子体积V0的意义:V0=
对于固体和液体指分子的体积,对于气体则指每个分子所占据空间的体积。
(2)物体的密度ρ的计算:ρ=
,但要切记
ρ=
是没有物理意义的。
例题:
解析
:
1.空气分子的平均质量为:
2.成年人做一次深呼吸所吸入的空气质量为:
3.所吸入的分子数为:
【例】已知氧气分子的质量m=5.3×10-26kg,标准状况下氧气的密度ρ=1.43
kg/m3,阿伏加德罗常数NA=6.02×1023mol-1,求:
(1)氧气的摩尔质量;
(2)标准状况下氧气分子间的平均距离;
(3)标准状况下1
cm3的氧气中含有的氧分子数.(保留两位有效数字)
答案
(1)3.2×10-2kg/mol
(2)3.3×10-9m (3)2.7×1019个
3.已知地球大气层的厚度h远小于地球半径R,空气平均摩尔质量为M,阿伏加德罗常数为NA,地面大气压强为p0,重力加速度大小为g。由此可估算得,地球大气层空气分子总数为__________,空气分子之间的平均距离为__________。
【解析】设大气层中气体的质量为m,由大气压强产生原因可知,mg=p0S,即:m=
分子数n=
,假设每个分子占据一个小立方体,各小立方体紧密排列,则小立方体边长即为空气分子平均间距,设为a,大气层中气体总体积为V,a=
,而V=4πR2h,所以a=
答案:
第七章
分子热运动
7.1
物体是由大量分子组成的
学习目标
1.知道可以用单分子油膜法测定分子直径.
2.知道阿伏加德罗常数的含义,并记住
这个常数的数值和单位.
3.知道一般分子的直径和质量的数量级.
4.会用阿伏加德罗常数、摩尔质量、摩尔
体积,估算分子大小或根据分子大小估算阿伏加德罗常数.
引入:
初中学过的有关分子运动的中,我们已知道物体是由大量分子组成的.
在热学中由于原子、离子、或分子做热运动时遵从相同的规律,所以统称为分子.
一、分子的大小
放大上亿倍的蛋白质分子结构模型
分子的体积是极其微小的,用肉眼和光学显微镜都不能看到;放大到几十亿倍的扫描隧道显微镜才能看到.
请阅读课文P69最下面一段
怎样才能知道分子的大小呢?
2.具体做法是:
将一滴体积已知的小油滴,
滴在水面上,
在重力作用下尽可能的散开形成一层极薄的油膜,
此时油膜可看成单分子油膜,油膜的厚度看成是油酸分子的直径,
所以只要再测定出这层油膜的面积,
就可求出油分子直径的大小.
1.有一种粗略测定分子大小的方法叫油膜法.
78cm2
实验原理:
若已知一滴油的体积V和水面上油膜面
积S,
那么这种油分子的直径d是多少?
分子直径d=
V/
S.
简化处理:
(1)把分子看成一个个小球;
(2)油分子一个紧挨一个整齐排列;
(3)认为油膜厚度等于分子直径.
?
(3)数量级:
一些数据太大或很小,为了书写方便,习惯上用科学记数法写成10的乘方数,如
3×10-10m。我们把10的乘方数叫做数量级,
1×10-10m和
9×10-10m,数量级都是
10-10m。
分子直径数量级:
除少数有机物大分子,一般分子直径的数量级是10-10m。
例:水分子直径是4×10-10m,
氢分子直径是2.3×10-10m
,
钨原子直径是2×10-10m.
例题1:在做“用油膜法估测分子大小”的实验时,油酸酒精溶液的浓度为每1
000mL溶液中有纯油酸0.1mL,用注射器测得1mL上述溶液有200滴,把一滴该溶液滴入盛水的表面撒有痱子粉的浅盘里,待水面稳定后,测得油酸膜的近似轮廓如图所示,图中正方形小方格的边长为1cm,则每一滴油酸酒精溶液中含有纯油酸的体积是________mL,油酸膜的面积是________cm2。根据上述数据,估测出油酸分子的直径是________m。
解析:每一滴油酸酒精溶液中含有纯油酸的体积为
V=
mL
=
5×10-7mL
油膜的面积S=40×1cm2=40cm2,
分子直径d=
m=1.25×10-10m。
答案:(1)C (2)5×10-7 40 1.25×10-10
【规律方法】油膜法估测分子直径问题的解答技巧
油膜法估测分子直径分三个过程:
(1)获得一滴油酸酒精溶液,并由配制浓度求出其中所含纯油酸的体积V。
(2)用数格子法(不足半个的舍去,多于半个的算一个,即“四舍五入”法)求出油膜面积S。
(3)由公式d=
计算结果。其中V和S的单位均采用国际单位制中的单位,即体积V的单位是m3,面积S的单位是m2。
【过关训练】
1.在“用油膜法估测分子的大小”的实验中,已知一滴溶液中油酸的体积为V,配制的油酸溶液中纯油酸与溶液体积之比为1︰500,1mL油酸溶液50滴,那么一滴溶液的体积是_____mL,所以一滴溶液中油酸体积为V=____cm3。
若实验中测得的结果如表所示,请根据所给数据填写空白处的数值,并与公认的油酸分子直径值d0=5.12×10-10m作比较,并判断此实验是否符合数量级的要求。
次数
S/cm2
d=
/×10-7cm
d平均值
1
538
2
545
3
563
【解析】1滴溶液的体积V溶液=
mL,
其中含油酸体积
V=
V溶液=4×10-5cm3,
据此算出3次测得的d值分别为
d1≈7.43×10-8cm,d2≈7.34×10-8cm,
d3≈7.10×10-8cm,其平均值
=7.29×10-8cm=7.29×10-10m,
这与公认值的数量级相吻合,故本次估测数值符合数量级的要求。
答案:
4×10-5
0.743
0.734
0.710 7.29×10-10m
符合
【典例示范】在“用单分子油膜估测单分子的大小”的实验中,按照酒精与油酸体积比为m︰n配制油酸酒精溶液,现用滴管滴取油酸酒精溶液,
N滴溶液的总体积为V。
(1)用滴管将一滴油酸酒精溶液滴入浅盘,待稳定后将油酸薄膜轮廓描绘在坐标纸上,如图所示。已知坐标纸上每个小方格面积为S,则油膜面积为_______。
(2)估算油酸分子直径的表达式为
________(用题目中物理量的字母表示)。
【正确解答】(1)根据坐标纸上油酸薄膜的轮廓,数出轮廓范围内正方形的个数为115(不足半个的舍去,多于半个的算一个),又因为坐标纸上每个方格面积为S,则油膜面积为S0=115S。
(2)设油酸的体积为V酸,油酸酒精溶液的浓度为
1滴油酸酒精溶液的体积V滴=
1滴油酸酒精溶液中纯油酸的体积为V0=
则估算油酸分子直径的表达式为d=
答案:(1)115S (2)
二、阿伏加德罗常数
1.阿伏加德罗常数NA:1摩尔(mol)任何物质所含的微粒数叫做阿伏加德罗常数.
2.阿伏加德罗常数是联系微观世界和宏观世界的桥梁.
(1)已知物质的摩尔质量MA,可求出分子质量m0
(其中,VA为摩尔体积,?为物质的密度)
(2)已知物质的量(摩尔数)n,可求出物体所含分子的数目N.
3.有关计算:
(3)已知物质的摩尔体积VA
,可求出分子的体积
V0
4.分子的简化模型:
实际分子的结构是很复杂的,且形状各异。但如果我们只关心分子的大小,而不涉及分子内部的结构和运动时,既可以把分子看成球形,也可以看成立方体。具体分析如下:
(1)对于固体和液体,可认为分子紧密排列,分子间没有空隙,则VA=NAV0(V0为一个分子的体积,VA为摩尔体积)。
①球形分子模型:如图所示,则直径d=
②立方体分子模型:认为每个分子占据一个相同的立方体空间,该立方体的边长即为分子间的平均距离,边长
d=
。如图所示。
(2)对于气体来说,由于气体分子间的距离远大于气体分子的直径,故通过立方体分子模型(不采用球形分子模型),可以估算得到每个气体分子平均占有的空间,而无法得到每个气体分子的实际体积。设每个气体分子占据的空间可看成一个边长为d、体积为V的正方体。气体分子间距离l=d=
,如图所示。(图中黑点代表气体分子所在的位置)
5.总结
阿伏加德罗常数的应用:
(1)微观量:分子质量m0,分子体积V0,分子直径d。
(2)宏观量:物质的质量M、体积V、密度ρ、摩尔质量MA、摩尔体积VA。
(3)微观量与宏观量的关系。
①分子质量:m0=
②分子体积:
(适用于固体和液体)。
③物质所含的分子数:
④阿伏加德罗常数:
(只适用于固体、液体)。
⑤气体分子间的平均距离:
(V0为气体分子所占据空间的体积)。
⑥固体、液体分子直径:
(V0为分子体积)。
【特别提醒】
(1)分子体积V0的意义:V0=
对于固体和液体指分子的体积,对于气体则指每个分子所占据空间的体积。
(2)物体的密度ρ的计算:ρ=
,但要切记
ρ=
是没有物理意义的。
例题:
解析
:
1.空气分子的平均质量为:
2.成年人做一次深呼吸所吸入的空气质量为:
3.所吸入的分子数为:
【例】已知氧气分子的质量m=5.3×10-26kg,标准状况下氧气的密度ρ=1.43
kg/m3,阿伏加德罗常数NA=6.02×1023mol-1,求:
(1)氧气的摩尔质量;
(2)标准状况下氧气分子间的平均距离;
(3)标准状况下1
cm3的氧气中含有的氧分子数.(保留两位有效数字)
答案
(1)3.2×10-2kg/mol
(2)3.3×10-9m (3)2.7×1019个
3.已知地球大气层的厚度h远小于地球半径R,空气平均摩尔质量为M,阿伏加德罗常数为NA,地面大气压强为p0,重力加速度大小为g。由此可估算得,地球大气层空气分子总数为__________,空气分子之间的平均距离为__________。
【解析】设大气层中气体的质量为m,由大气压强产生原因可知,mg=p0S,即:m=
分子数n=
,假设每个分子占据一个小立方体,各小立方体紧密排列,则小立方体边长即为空气分子平均间距,设为a,大气层中气体总体积为V,a=
,而V=4πR2h,所以a=
答案:
