人教B版数学必修二本册综合测试一附解析
文档属性
| 名称 | 人教B版数学必修二本册综合测试一附解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 404.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-16 00:00:00 | ||
图片预览




文档简介
本册综合测试一
时间:120分钟 满分:150分
一、选择题(本大题共12小题,每小题5分,共60分)
1.下列关于直线l,m与平面α,β的命题中,正确的是( )
A.若l?β,且α⊥β,则l⊥α
B.若l⊥β,且α∥β,则l⊥α
C.若l⊥β,且α⊥β,则l∥α
D.若α∩β=m,且l∥m,则l∥α
2.如果直线ax+2y+2=0与直线3x-y-2=0平行,则系数a=( )
A.-3
B.-6
C.-
D.
3.如下图所示,观察四个几何体,其中判断正确的是( )
A.①是棱台
B.②是圆台
C.③是棱锥
D.④是棱台
4.圆柱底面圆的半径和圆柱的高都为2,则圆柱侧面展开图的面积为( )
A.4π
B.4π
C.8π
D.8π
5.设P为圆x2+y2=1上的动点,则点P到直线3x-4y-20=0的距离的最小值为( )
A.2
B.3
C.4
D.5
6.一个几何体的三视图如图所示,则该几何体的体积为( )
A.
B.
C.
D.
7.在空间直角坐标系中,方程x2-4(y-1)2=0表示的图形是( )
A.两个点
B.两条直线
C.两个平面
D.一条直线和一个平面
8.某直三棱柱的侧棱长等于2,底面为等腰直角三角形且腰长为1,则该直三棱柱的外接球的表面积是( )
A.π
B.2π
C.4π
D.6π
9.已知直线l:2x+3y+1=0被圆C:x2+y2=r2所截得的弦长为d,则下列直线中被圆C截得的弦长同样为d的直线是( )
A.4x+6y-1=0
B.4x+6y+1=0
C.2x-3y-1=0
D.3x+2y=0
10.直线y=x+b与曲线x=有且仅有一个公共点,则b的取值范围是( )
A.|b|=2
B.-1C.-1≤b≤1
D.以上答案都不对
11.以M(-4,3)为圆心的圆与直线2x+y-5=0相离,那么圆M的半径r的取值范围是( )
A.0B.0C.0D.012.已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论不正确的是( )
A.CD∥平面PAF
B.DF⊥平面PAF
C.CF∥平面PAB
D.CF⊥平面PAD
二、填空题(本大题共4小题,每小题5分,共20分)
13.空间两点A(2,5,4),B(-2,3,5)之间的距离等于________.
14.若圆(x-3)2+(y+5)2=r2(r>0)上有且仅有两个点到直线4x-3y-2=0的距离为1,则半径r的取值范围是________________.
15.已知一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为________.
16.已知⊙O的方程是x2+y2-2=0,⊙O′的方程是x2+y2-8x+10=0,由动点P向⊙O和⊙O′所引的切线长相等,则动点P的轨迹方程是________.
三、解答题(本大题共6小题,共70分)
17.(10分)在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余的体积之比.
18.(12分)已知直线l经过点M(-3,-3),且圆x2+y2+4y-21=0的圆心到l的距离为.
(1)求直线l被该圆所截得的弦长;
(2)求直线l的方程.
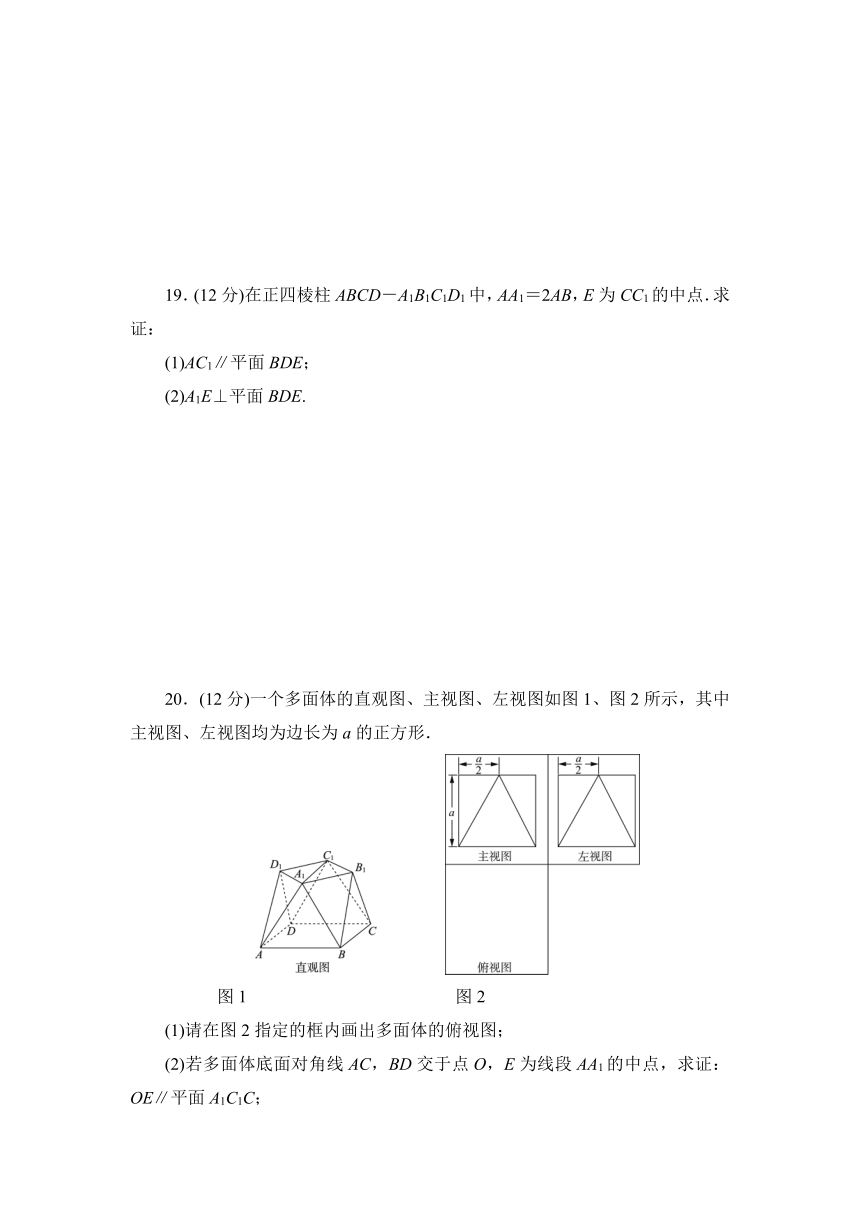
19.(12分)在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点.求证:
(1)AC1∥平面BDE;
(2)A1E⊥平面BDE.
20.(12分)一个多面体的直观图、主视图、左视图如图1、图2所示,其中主视图、左视图均为边长为a的正方形.
图1
图2
(1)请在图2指定的框内画出多面体的俯视图;
(2)若多面体底面对角线AC,BD交于点O,E为线段AA1的中点,求证:OE∥平面A1C1C;
(3)求该多面体的表面积.
21.(12分)在直角坐标系xOy中,已知圆C:(x-2)2+(y-2)2=8及点O(0,0),A(-2,0).
(1)从圆C外一点M(m,n)向圆C引一条切线,切点为B,且|MB|=|MA|,求|MO|的最小值;
(2)设点T(0,t)满足:存在圆C上的两点P、Q,使得+=,求实数t的取值范围.
22.(12分)已知以点C(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M,N,若|OM|=|ON|,求圆C的方程;
(3)在(2)的条件下,设P,Q分别是直线l:x+y+2=0和圆C的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
本册综合测试一
时间:120分钟 满分:150分
一、选择题(本大题共12小题,每小题5分,共60分)
1.下列关于直线l,m与平面α,β的命题中,正确的是( )
A.若l?β,且α⊥β,则l⊥α
B.若l⊥β,且α∥β,则l⊥α
C.若l⊥β,且α⊥β,则l∥α
D.若α∩β=m,且l∥m,则l∥α
答案:B
2.如果直线ax+2y+2=0与直线3x-y-2=0平行,则系数a=( )
A.-3
B.-6
C.-
D.
解析:B 由题可得=≠,∴a=-6,故选B.
3.如下图所示,观察四个几何体,其中判断正确的是( )
A.①是棱台
B.②是圆台
C.③是棱锥
D.④是棱台
答案:C
4.圆柱底面圆的半径和圆柱的高都为2,则圆柱侧面展开图的面积为( )
A.4π
B.4π
C.8π
D.8π
解析:C S侧=2πrl=2π×2×2=8π.
5.设P为圆x2+y2=1上的动点,则点P到直线3x-4y-20=0的距离的最小值为( )
A.2
B.3
C.4
D.5
解析:B 圆心到直线3x-4y-20=0的距离为d==4,所以点P到直线3x-4y-20=0距离的最小值为d-1=3,故选B.
6.一个几何体的三视图如图所示,则该几何体的体积为( )
A.
B.
C.
D.
解析:A 该几何体是一个三棱柱截去一个三棱锥,V=×2××2-××2××1=,故选A.
7.在空间直角坐标系中,方程x2-4(y-1)2=0表示的图形是( )
A.两个点
B.两条直线
C.两个平面
D.一条直线和一个平面
解析:C 由原方程可得(x+2y-2)(x-2y+2)=0,
∴x+2y-2=0或x-2y+2=0.故选C.
8.某直三棱柱的侧棱长等于2,底面为等腰直角三角形且腰长为1,则该直三棱柱的外接球的表面积是( )
A.π
B.2π
C.4π
D.6π
解析:D 如图,∵直三棱柱的底面是等腰直角三角形,底面外接圆的半径r=AC=,
设球的半径为R,则R2=r2+12=,
∴S球=4πR2=4π×=6π,故选D.
9.已知直线l:2x+3y+1=0被圆C:x2+y2=r2所截得的弦长为d,则下列直线中被圆C截得的弦长同样为d的直线是( )
A.4x+6y-1=0
B.4x+6y+1=0
C.2x-3y-1=0
D.3x+2y=0
解析:C 圆心(0,0)到直线l的距离为d′==,A中,d1==,B中,d2==,C中,d3==,D中,d4=0,故选C.
10.直线y=x+b与曲线x=有且仅有一个公共点,则b的取值范围是( )
A.|b|=2
B.-1C.-1≤b≤1
D.以上答案都不对
解析:B 曲线x=可得x2+y2=1(x≥0),表示半圆,如图所示,y=x+b与曲线只有一个公共点,则-111.以M(-4,3)为圆心的圆与直线2x+y-5=0相离,那么圆M的半径r的取值范围是( )
A.0B.0C.0D.0解析:C 由题可得r<=2,故选C.
12.已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论不正确的是( )
A.CD∥平面PAF
B.DF⊥平面PAF
C.CF∥平面PAB
D.CF⊥平面PAD
解析:D ∵CD∥AF,∴CD∥平面PAF,故A正确;
∵DF⊥AF,DF⊥PA,AF∩AP=A,∴DF⊥平面PAF,故B正确;CF∥AB,∴CF∥平面PAB,故C正确,D不正确.
二、填空题(本大题共4小题,每小题5分,共20分)
13.空间两点A(2,5,4),B(-2,3,5)之间的距离等于________.
解析:|AB|==.
答案:
14.若圆(x-3)2+(y+5)2=r2(r>0)上有且仅有两个点到直线4x-3y-2=0的距离为1,则半径r的取值范围是________________.
解析:圆心(3,-5)到直线4x-3y-2=0的距离为d==5,所以当4答案:(4,6)
15.已知一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为________.
解析:设正方体的棱长为a,球的半径为r,
则πr3=,∴r=,
又3a2=4r2=9,∴a2=3,
∴a=.
答案:
16.已知⊙O的方程是x2+y2-2=0,⊙O′的方程是x2+y2-8x+10=0,由动点P向⊙O和⊙O′所引的切线长相等,则动点P的轨迹方程是________.
解析:设动点P的坐标为(x,y).由动点P向圆x2+y2=2引切线,切线长为;由点P向圆(x-4)2+y2=6引切线,切线长为.
由=,得x=.
答案:x=
三、解答题(本大题共6小题,共70分)
17.(10分)在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余的体积之比.
解:已知长方体是直四棱柱,
设它的底面ADD1A1的面积为S,高为h,
则它的体积为V=Sh.
而棱锥C-A1DD1的底面积为S,高为h,
故三棱锥C-A1DD1的体积:
VC-A1DD1=×Sh=Sh,
余下部分体积为Sh-Sh=Sh.
所以棱锥C-A1DD1的体积与剩余部分的体积之比为1∶5.
18.(12分)已知直线l经过点M(-3,-3),且圆x2+y2+4y-21=0的圆心到l的距离为.
(1)求直线l被该圆所截得的弦长;
(2)求直线l的方程.
解:(1)圆的方程可化为x2+(y+2)2=25,
∴圆心为(0,-2),r=5,直线l被圆所截得的弦长为2=4.
(2)设直线l:y+3=k(x+3),∴kx-y+3k-3=0,
∴=,∴k=2或k=-.
∴l的方程为2x-y+3=0或x+2y+9=0.
19.(12分)在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点.求证:
(1)AC1∥平面BDE;
(2)A1E⊥平面BDE.
证明:(1)连接AC交BD于O,连接OE,
∵O为AC的中点,E为CC1的中点,
∴OE∥AC1,
又OE?平面BDE,AC1?平面BDE,
∴AC1∥平面BDE.
(2)∵底面ABCD是正方形,
∴AC⊥BD,
又∵BD⊥AA1,AA1∩AC=A,
∴BD⊥平面ACC1A1,A1E?平面ACC1A,
∴BD⊥A1E.
设AA1=2AB=2a,
∴BE=a,
A1E==a.
A1B==a,
∴A1B2=A1E2+BE2,
∵A1E⊥BE,BD∩BE=B.
∴A1E⊥平面BDE.
20.(12分)一个多面体的直观图、主视图、左视图如图1、图2所示,其中主视图、左视图均为边长为a的正方形.
图1
图2
(1)请在图2指定的框内画出多面体的俯视图;
(2)若多面体底面对角线AC,BD交于点O,E为线段AA1的中点,求证:OE∥平面A1C1C;
(3)求该多面体的表面积.
解:(1)根据多面体的直观图、主视图、左视图,得到俯视图如下:
(2)证明:如图,连接AC,BD,交于O点,连接OE.
∵E为AA1的中点,O为AC的中点,
∴在△AA1C中,OE为△AA1C的中位线.
∴OE∥A1C.
∵OE?平面A1C1C,A1C?平面A1C1C,
∴OE∥平面A1C1C.
(3)多面体表面共包括10个面,
S△ABCD=a2,SA1B1C1D1=,
S△ABA1=S△B1BC=S△C1DC=S△ADD1=,
S△AA1D1=S△B1A1B=S△C1B1C=S△D
C1D1=××=,
∴该多面体的表面积S=a2++4×+4×=5a2.
21.(12分)在直角坐标系xOy中,已知圆C:(x-2)2+(y-2)2=8及点O(0,0),A(-2,0).
(1)从圆C外一点M(m,n)向圆C引一条切线,切点为B,且|MB|=|MA|,求|MO|的最小值;
(2)设点T(0,t)满足:存在圆C上的两点P、Q,使得+=,求实数t的取值范围.
解:(1)由题意知|MA|2=|MC|2-8即(m+2)2+n2=(m-2)2+(n-2)2-8,得2m+n+1=0,即M(m,n)在直线2x+y+1=0上,|MO|min==.
(2)设P(x1,y1)、Q(x2,y2),=(-2,-t),=(x1,y1-t),=(x2,y2-t),+=,
得又P(x1,y1)、Q(x2,y2)均在圆C上,
即
若这样的点T(0,t)存在,即是圆(x-2)2+(y-2)2=8与圆(x-4)2+(y-t-2)2=8有交点,
故0≤≤2+2,即≤4,∴t∈[-2,2].
22.(12分)已知以点C(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M,N,若|OM|=|ON|,求圆C的方程;
(3)在(2)的条件下,设P,Q分别是直线l:x+y+2=0和圆C的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
解:(1)证明:由题设知,圆C的方程为(x-t)2+2=t2+,化简得x2-2tx+y2-y=0,
当y=0时,x=0或2t,则A(2t,0);当x=0时,y=0或,则B,
∴S△AOB=|OA|·|OB|=|2t|·=4为定值.
(2)∵|OM|=|ON|,则原点O在MN的中垂线上,设MN的中点为H,则CH⊥MN,∴C,H,O三点共线,则直线OC的斜率k===,∴t=2或t=-2.∴圆心为C(2,1)或(-2,-1),∴圆C的方程为(x-2)2+(y-1)2=5或(x+2)2+(y+1)2=5,
由于当圆C的方程为(x+2)2+(y+1)2=5时,直线2x+y-4=0到圆心的距离d>r,此时不满足直线与圆相交,故舍去,∴圆C的方程为(x-2)2+(y-1)2=5.
(3)点B(0,2)关于直线x+y+2=0的对称点为B′(-4,-2),则|PB|+|PQ|=|PB′|+|PQ|≥|B′Q|,又B′到圆上点Q的最短距离为|B′C|-r=-=3-=2.所以|PB|+|PQ|的最小值为2,直线B′C的方程为y=x,则直线B′C与直线x+y+2=0的交点P此时的坐标为.
时间:120分钟 满分:150分
一、选择题(本大题共12小题,每小题5分,共60分)
1.下列关于直线l,m与平面α,β的命题中,正确的是( )
A.若l?β,且α⊥β,则l⊥α
B.若l⊥β,且α∥β,则l⊥α
C.若l⊥β,且α⊥β,则l∥α
D.若α∩β=m,且l∥m,则l∥α
2.如果直线ax+2y+2=0与直线3x-y-2=0平行,则系数a=( )
A.-3
B.-6
C.-
D.
3.如下图所示,观察四个几何体,其中判断正确的是( )
A.①是棱台
B.②是圆台
C.③是棱锥
D.④是棱台
4.圆柱底面圆的半径和圆柱的高都为2,则圆柱侧面展开图的面积为( )
A.4π
B.4π
C.8π
D.8π
5.设P为圆x2+y2=1上的动点,则点P到直线3x-4y-20=0的距离的最小值为( )
A.2
B.3
C.4
D.5
6.一个几何体的三视图如图所示,则该几何体的体积为( )
A.
B.
C.
D.
7.在空间直角坐标系中,方程x2-4(y-1)2=0表示的图形是( )
A.两个点
B.两条直线
C.两个平面
D.一条直线和一个平面
8.某直三棱柱的侧棱长等于2,底面为等腰直角三角形且腰长为1,则该直三棱柱的外接球的表面积是( )
A.π
B.2π
C.4π
D.6π
9.已知直线l:2x+3y+1=0被圆C:x2+y2=r2所截得的弦长为d,则下列直线中被圆C截得的弦长同样为d的直线是( )
A.4x+6y-1=0
B.4x+6y+1=0
C.2x-3y-1=0
D.3x+2y=0
10.直线y=x+b与曲线x=有且仅有一个公共点,则b的取值范围是( )
A.|b|=2
B.-1
D.以上答案都不对
11.以M(-4,3)为圆心的圆与直线2x+y-5=0相离,那么圆M的半径r的取值范围是( )
A.0
A.CD∥平面PAF
B.DF⊥平面PAF
C.CF∥平面PAB
D.CF⊥平面PAD
二、填空题(本大题共4小题,每小题5分,共20分)
13.空间两点A(2,5,4),B(-2,3,5)之间的距离等于________.
14.若圆(x-3)2+(y+5)2=r2(r>0)上有且仅有两个点到直线4x-3y-2=0的距离为1,则半径r的取值范围是________________.
15.已知一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为________.
16.已知⊙O的方程是x2+y2-2=0,⊙O′的方程是x2+y2-8x+10=0,由动点P向⊙O和⊙O′所引的切线长相等,则动点P的轨迹方程是________.
三、解答题(本大题共6小题,共70分)
17.(10分)在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余的体积之比.
18.(12分)已知直线l经过点M(-3,-3),且圆x2+y2+4y-21=0的圆心到l的距离为.
(1)求直线l被该圆所截得的弦长;
(2)求直线l的方程.
19.(12分)在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点.求证:
(1)AC1∥平面BDE;
(2)A1E⊥平面BDE.
20.(12分)一个多面体的直观图、主视图、左视图如图1、图2所示,其中主视图、左视图均为边长为a的正方形.
图1
图2
(1)请在图2指定的框内画出多面体的俯视图;
(2)若多面体底面对角线AC,BD交于点O,E为线段AA1的中点,求证:OE∥平面A1C1C;
(3)求该多面体的表面积.
21.(12分)在直角坐标系xOy中,已知圆C:(x-2)2+(y-2)2=8及点O(0,0),A(-2,0).
(1)从圆C外一点M(m,n)向圆C引一条切线,切点为B,且|MB|=|MA|,求|MO|的最小值;
(2)设点T(0,t)满足:存在圆C上的两点P、Q,使得+=,求实数t的取值范围.
22.(12分)已知以点C(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M,N,若|OM|=|ON|,求圆C的方程;
(3)在(2)的条件下,设P,Q分别是直线l:x+y+2=0和圆C的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
本册综合测试一
时间:120分钟 满分:150分
一、选择题(本大题共12小题,每小题5分,共60分)
1.下列关于直线l,m与平面α,β的命题中,正确的是( )
A.若l?β,且α⊥β,则l⊥α
B.若l⊥β,且α∥β,则l⊥α
C.若l⊥β,且α⊥β,则l∥α
D.若α∩β=m,且l∥m,则l∥α
答案:B
2.如果直线ax+2y+2=0与直线3x-y-2=0平行,则系数a=( )
A.-3
B.-6
C.-
D.
解析:B 由题可得=≠,∴a=-6,故选B.
3.如下图所示,观察四个几何体,其中判断正确的是( )
A.①是棱台
B.②是圆台
C.③是棱锥
D.④是棱台
答案:C
4.圆柱底面圆的半径和圆柱的高都为2,则圆柱侧面展开图的面积为( )
A.4π
B.4π
C.8π
D.8π
解析:C S侧=2πrl=2π×2×2=8π.
5.设P为圆x2+y2=1上的动点,则点P到直线3x-4y-20=0的距离的最小值为( )
A.2
B.3
C.4
D.5
解析:B 圆心到直线3x-4y-20=0的距离为d==4,所以点P到直线3x-4y-20=0距离的最小值为d-1=3,故选B.
6.一个几何体的三视图如图所示,则该几何体的体积为( )
A.
B.
C.
D.
解析:A 该几何体是一个三棱柱截去一个三棱锥,V=×2××2-××2××1=,故选A.
7.在空间直角坐标系中,方程x2-4(y-1)2=0表示的图形是( )
A.两个点
B.两条直线
C.两个平面
D.一条直线和一个平面
解析:C 由原方程可得(x+2y-2)(x-2y+2)=0,
∴x+2y-2=0或x-2y+2=0.故选C.
8.某直三棱柱的侧棱长等于2,底面为等腰直角三角形且腰长为1,则该直三棱柱的外接球的表面积是( )
A.π
B.2π
C.4π
D.6π
解析:D 如图,∵直三棱柱的底面是等腰直角三角形,底面外接圆的半径r=AC=,
设球的半径为R,则R2=r2+12=,
∴S球=4πR2=4π×=6π,故选D.
9.已知直线l:2x+3y+1=0被圆C:x2+y2=r2所截得的弦长为d,则下列直线中被圆C截得的弦长同样为d的直线是( )
A.4x+6y-1=0
B.4x+6y+1=0
C.2x-3y-1=0
D.3x+2y=0
解析:C 圆心(0,0)到直线l的距离为d′==,A中,d1==,B中,d2==,C中,d3==,D中,d4=0,故选C.
10.直线y=x+b与曲线x=有且仅有一个公共点,则b的取值范围是( )
A.|b|=2
B.-1
D.以上答案都不对
解析:B 曲线x=可得x2+y2=1(x≥0),表示半圆,如图所示,y=x+b与曲线只有一个公共点,则-1
A.0
12.已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论不正确的是( )
A.CD∥平面PAF
B.DF⊥平面PAF
C.CF∥平面PAB
D.CF⊥平面PAD
解析:D ∵CD∥AF,∴CD∥平面PAF,故A正确;
∵DF⊥AF,DF⊥PA,AF∩AP=A,∴DF⊥平面PAF,故B正确;CF∥AB,∴CF∥平面PAB,故C正确,D不正确.
二、填空题(本大题共4小题,每小题5分,共20分)
13.空间两点A(2,5,4),B(-2,3,5)之间的距离等于________.
解析:|AB|==.
答案:
14.若圆(x-3)2+(y+5)2=r2(r>0)上有且仅有两个点到直线4x-3y-2=0的距离为1,则半径r的取值范围是________________.
解析:圆心(3,-5)到直线4x-3y-2=0的距离为d==5,所以当4
15.已知一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为________.
解析:设正方体的棱长为a,球的半径为r,
则πr3=,∴r=,
又3a2=4r2=9,∴a2=3,
∴a=.
答案:
16.已知⊙O的方程是x2+y2-2=0,⊙O′的方程是x2+y2-8x+10=0,由动点P向⊙O和⊙O′所引的切线长相等,则动点P的轨迹方程是________.
解析:设动点P的坐标为(x,y).由动点P向圆x2+y2=2引切线,切线长为;由点P向圆(x-4)2+y2=6引切线,切线长为.
由=,得x=.
答案:x=
三、解答题(本大题共6小题,共70分)
17.(10分)在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余的体积之比.
解:已知长方体是直四棱柱,
设它的底面ADD1A1的面积为S,高为h,
则它的体积为V=Sh.
而棱锥C-A1DD1的底面积为S,高为h,
故三棱锥C-A1DD1的体积:
VC-A1DD1=×Sh=Sh,
余下部分体积为Sh-Sh=Sh.
所以棱锥C-A1DD1的体积与剩余部分的体积之比为1∶5.
18.(12分)已知直线l经过点M(-3,-3),且圆x2+y2+4y-21=0的圆心到l的距离为.
(1)求直线l被该圆所截得的弦长;
(2)求直线l的方程.
解:(1)圆的方程可化为x2+(y+2)2=25,
∴圆心为(0,-2),r=5,直线l被圆所截得的弦长为2=4.
(2)设直线l:y+3=k(x+3),∴kx-y+3k-3=0,
∴=,∴k=2或k=-.
∴l的方程为2x-y+3=0或x+2y+9=0.
19.(12分)在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点.求证:
(1)AC1∥平面BDE;
(2)A1E⊥平面BDE.
证明:(1)连接AC交BD于O,连接OE,
∵O为AC的中点,E为CC1的中点,
∴OE∥AC1,
又OE?平面BDE,AC1?平面BDE,
∴AC1∥平面BDE.
(2)∵底面ABCD是正方形,
∴AC⊥BD,
又∵BD⊥AA1,AA1∩AC=A,
∴BD⊥平面ACC1A1,A1E?平面ACC1A,
∴BD⊥A1E.
设AA1=2AB=2a,
∴BE=a,
A1E==a.
A1B==a,
∴A1B2=A1E2+BE2,
∵A1E⊥BE,BD∩BE=B.
∴A1E⊥平面BDE.
20.(12分)一个多面体的直观图、主视图、左视图如图1、图2所示,其中主视图、左视图均为边长为a的正方形.
图1
图2
(1)请在图2指定的框内画出多面体的俯视图;
(2)若多面体底面对角线AC,BD交于点O,E为线段AA1的中点,求证:OE∥平面A1C1C;
(3)求该多面体的表面积.
解:(1)根据多面体的直观图、主视图、左视图,得到俯视图如下:
(2)证明:如图,连接AC,BD,交于O点,连接OE.
∵E为AA1的中点,O为AC的中点,
∴在△AA1C中,OE为△AA1C的中位线.
∴OE∥A1C.
∵OE?平面A1C1C,A1C?平面A1C1C,
∴OE∥平面A1C1C.
(3)多面体表面共包括10个面,
S△ABCD=a2,SA1B1C1D1=,
S△ABA1=S△B1BC=S△C1DC=S△ADD1=,
S△AA1D1=S△B1A1B=S△C1B1C=S△D
C1D1=××=,
∴该多面体的表面积S=a2++4×+4×=5a2.
21.(12分)在直角坐标系xOy中,已知圆C:(x-2)2+(y-2)2=8及点O(0,0),A(-2,0).
(1)从圆C外一点M(m,n)向圆C引一条切线,切点为B,且|MB|=|MA|,求|MO|的最小值;
(2)设点T(0,t)满足:存在圆C上的两点P、Q,使得+=,求实数t的取值范围.
解:(1)由题意知|MA|2=|MC|2-8即(m+2)2+n2=(m-2)2+(n-2)2-8,得2m+n+1=0,即M(m,n)在直线2x+y+1=0上,|MO|min==.
(2)设P(x1,y1)、Q(x2,y2),=(-2,-t),=(x1,y1-t),=(x2,y2-t),+=,
得又P(x1,y1)、Q(x2,y2)均在圆C上,
即
若这样的点T(0,t)存在,即是圆(x-2)2+(y-2)2=8与圆(x-4)2+(y-t-2)2=8有交点,
故0≤≤2+2,即≤4,∴t∈[-2,2].
22.(12分)已知以点C(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M,N,若|OM|=|ON|,求圆C的方程;
(3)在(2)的条件下,设P,Q分别是直线l:x+y+2=0和圆C的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
解:(1)证明:由题设知,圆C的方程为(x-t)2+2=t2+,化简得x2-2tx+y2-y=0,
当y=0时,x=0或2t,则A(2t,0);当x=0时,y=0或,则B,
∴S△AOB=|OA|·|OB|=|2t|·=4为定值.
(2)∵|OM|=|ON|,则原点O在MN的中垂线上,设MN的中点为H,则CH⊥MN,∴C,H,O三点共线,则直线OC的斜率k===,∴t=2或t=-2.∴圆心为C(2,1)或(-2,-1),∴圆C的方程为(x-2)2+(y-1)2=5或(x+2)2+(y+1)2=5,
由于当圆C的方程为(x+2)2+(y+1)2=5时,直线2x+y-4=0到圆心的距离d>r,此时不满足直线与圆相交,故舍去,∴圆C的方程为(x-2)2+(y-1)2=5.
(3)点B(0,2)关于直线x+y+2=0的对称点为B′(-4,-2),则|PB|+|PQ|=|PB′|+|PQ|≥|B′Q|,又B′到圆上点Q的最短距离为|B′C|-r=-=3-=2.所以|PB|+|PQ|的最小值为2,直线B′C的方程为y=x,则直线B′C与直线x+y+2=0的交点P此时的坐标为.
