人教B版数学必修二第1章 章末检测附解析
文档属性
| 名称 | 人教B版数学必修二第1章 章末检测附解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 463.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-16 00:00:00 | ||
图片预览


文档简介
第一章章
末
检
测
(时间:60分钟
满分:100分)
一、选择题(每小题5分,共40分)
1.设直线m,n和平面α,β,下列四个命题中,正确的是( )
A.若m∥α,n∥α,则m∥n
B.m?α,n?α,m∥β,n∥β,则α∥β
C.若α⊥β,m?α,则m⊥β
D.α⊥β,m⊥β,m?α,则m∥α
2.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的主视图(等腰直角三角形)和左视图,且该几何体的体积为,则该几何体的俯视图可以是( )
3.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题正确的是( )
A.若m⊥n,m⊥α,n∥β,则α∥β
B.若m∥n,m∥α,n∥β,则α∥β
C.若m⊥α,n∥β,α∥β,则m⊥n
D.若m∥α,n∥β,α∥β,则m∥n
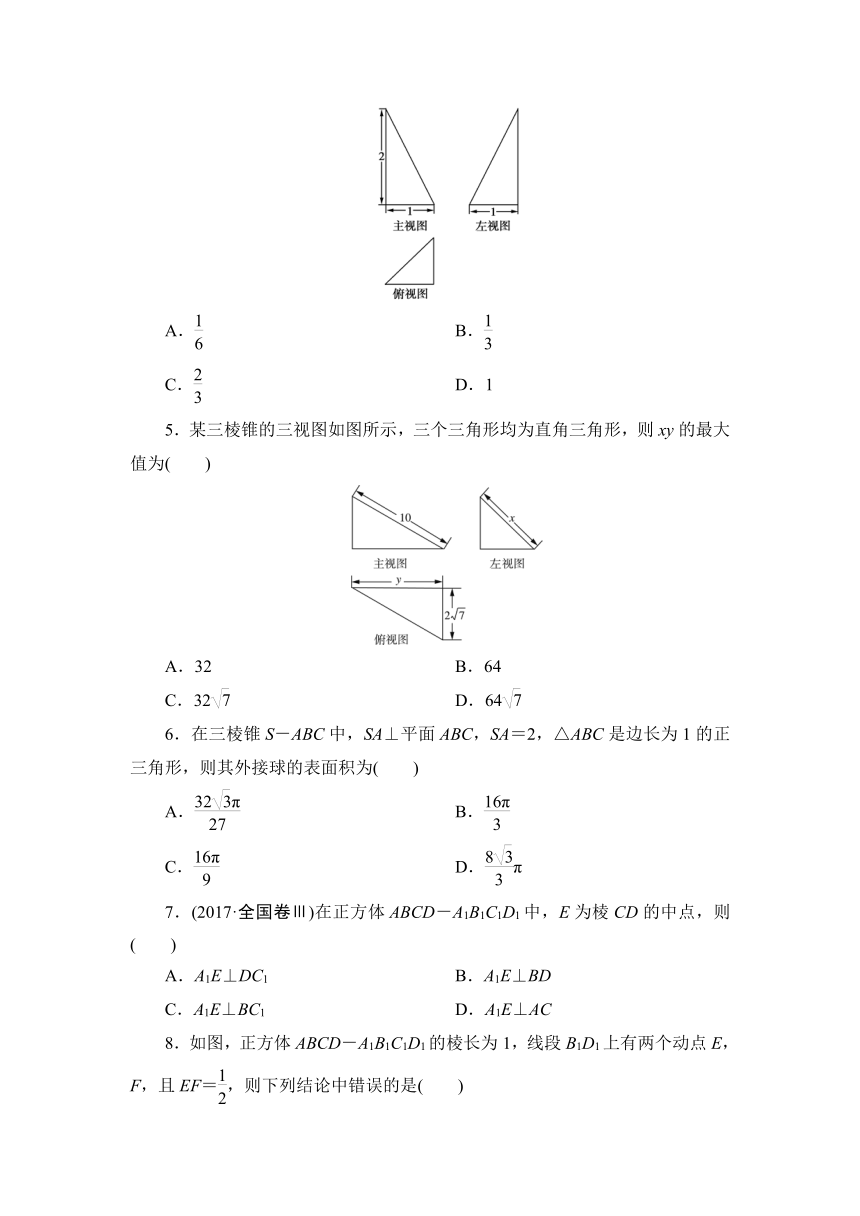
4.某三棱锥的三视图如图所示,则该三棱锥的体积是( )
A.
B.
C.
D.1
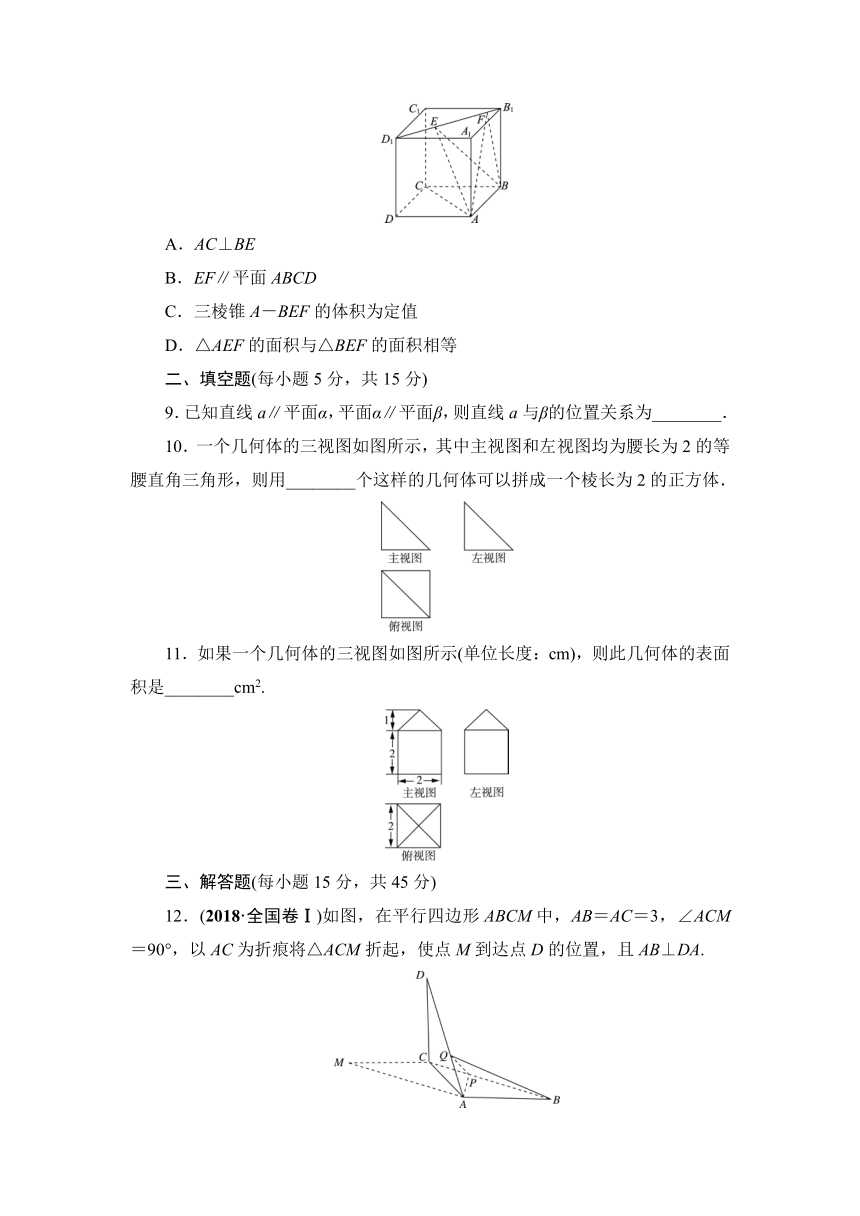
5.某三棱锥的三视图如图所示,三个三角形均为直角三角形,则xy的最大值为( )
A.32
B.64
C.32
D.64
6.在三棱锥S-ABC中,SA⊥平面ABC,SA=2,△ABC是边长为1的正三角形,则其外接球的表面积为( )
A.
B.
C.
D.π
7.(2017·全国卷Ⅲ)在正方体ABCD-A1B1C1D1中,E为棱CD的中点,则( )
A.A1E⊥DC1
B.A1E⊥BD
C.A1E⊥BC1
D.A1E⊥AC
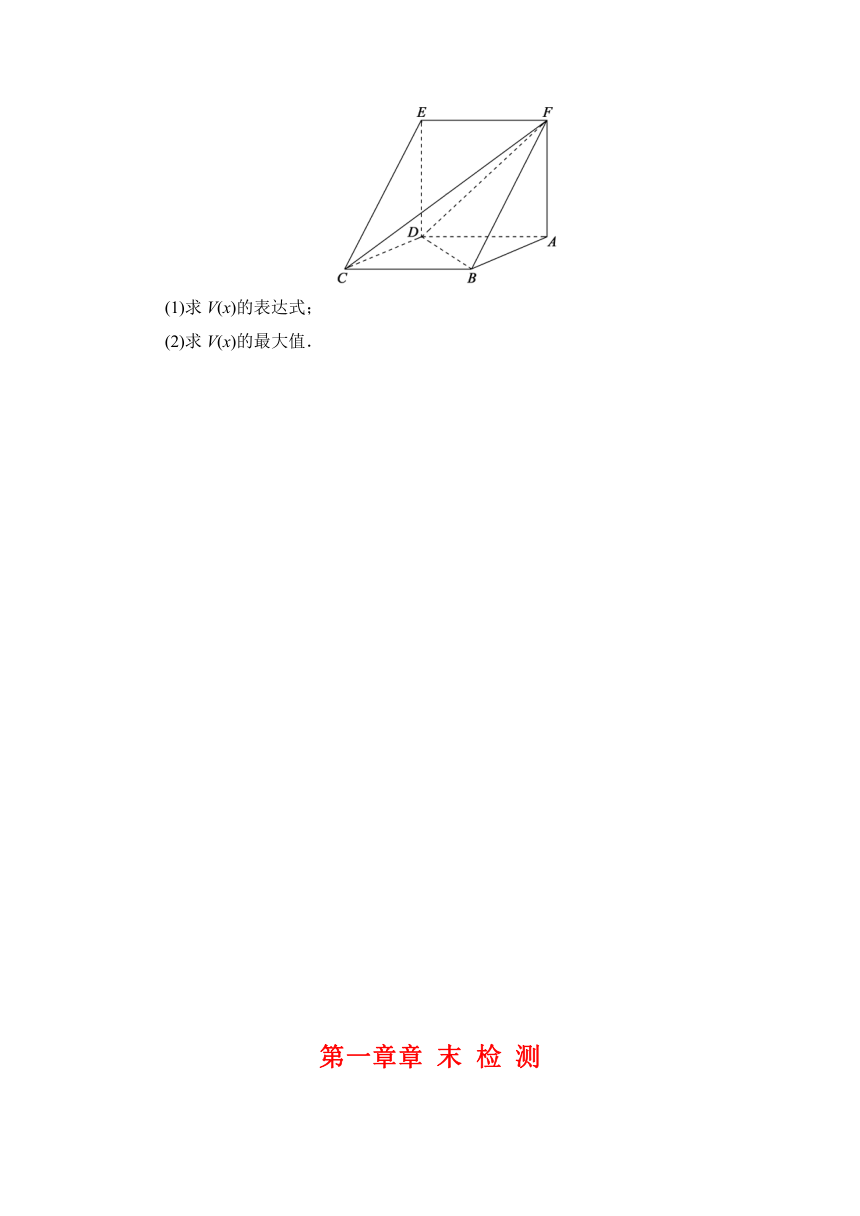
8.如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=,则下列结论中错误的是( )
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值
D.△AEF的面积与△BEF的面积相等
二、填空题(每小题5分,共15分)
9.已知直线a∥平面α,平面α∥平面β,则直线a与β的位置关系为________.
10.一个几何体的三视图如图所示,其中主视图和左视图均为腰长为2的等腰直角三角形,则用________个这样的几何体可以拼成一个棱长为2的正方体.
11.如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是________cm2.
三、解答题(每小题15分,共45分)
12.(2018·全国卷Ⅰ)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°,以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.
(1)证明:平面ACD⊥平面ABC;
(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ=DA,求三棱锥Q-ABP的体积.
13.如图(1)矩形ABCD中,AB=2AD=2a,E为DC的中点,现将△ADE沿AE折起,使平面ADE⊥平面ABCE,如图(2).
(1)求四棱锥D-ABCE的体积;
(2)求证:AD⊥平面BDE.
14.如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,记CD=x,V(x)表示四棱锥F-ABCD的体积.
(1)求V(x)的表达式;
(2)求V(x)的最大值.
第一章章
末
检
测
(时间:60分钟
满分:100分)
一、选择题(每小题5分,共40分)
1.设直线m,n和平面α,β,下列四个命题中,正确的是( )
A.若m∥α,n∥α,则m∥n
B.m?α,n?α,m∥β,n∥β,则α∥β
C.若α⊥β,m?α,则m⊥β
D.α⊥β,m⊥β,m?α,则m∥α
答案:D
2.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的主视图(等腰直角三角形)和左视图,且该几何体的体积为,则该几何体的俯视图可以是( )
解析:D 如图所示,将几何体放入正方体内,正方体的棱长为2,体积为8,当俯视图为是D选项时,该几何体是四棱锥E-ABCD,VE-ABCD=×2×2×2=,符合题意,故选D.
3.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题正确的是( )
A.若m⊥n,m⊥α,n∥β,则α∥β
B.若m∥n,m∥α,n∥β,则α∥β
C.若m⊥α,n∥β,α∥β,则m⊥n
D.若m∥α,n∥β,α∥β,则m∥n
解析:C C中由m⊥α,α∥β,可知m⊥β,又n∥β,∴m⊥n,故C正确.
4.某三棱锥的三视图如图所示,则该三棱锥的体积是( )
A.
B.
C.
D.1
解析:B 由三视图可知三棱锥的底面为等腰直角三角形,高为2,则V=××1×1×2=,故选B.
5.某三棱锥的三视图如图所示,三个三角形均为直角三角形,则xy的最大值为( )
A.32
B.64
C.32
D.64
解析:B 设该几何体的高为h,则
∴x2y2=(102-h2)(28+h2)=-h4+72h2+280,∴h2=36时,xy的最大值为64,故选B.
6.在三棱锥S-ABC中,SA⊥平面ABC,SA=2,△ABC是边长为1的正三角形,则其外接球的表面积为( )
A.
B.
C.
D.π
解析:B ∵△ABC为正三角形,
∴△ABC的外接圆的半径为××1=.
设外接球的半径为R,
则R2=2+2=.
∴S球=4πR2=.故选B.
7.(2017·全国卷Ⅲ)在正方体ABCD-A1B1C1D1中,E为棱CD的中点,则( )
A.A1E⊥DC1
B.A1E⊥BD
C.A1E⊥BC1
D.A1E⊥AC
解析:C 由正方体的性质,得A1B1⊥BC1,B1C⊥BC1,所以BC1⊥平面A1B1CD,又A1E?平面A1B1CD,所以A1E⊥BC1,故选C.
8.如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=,则下列结论中错误的是( )
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值
D.△AEF的面积与△BEF的面积相等
解析:D ∵AC⊥BD,BB1⊥底面ABCD,∴BB1⊥AC,∴AC⊥平面B1D1D,BE?面BDD1B1,∴AC⊥BE,A正确;∵EF∥BD,∴EF∥平面ABCD,B正确;A到平面BEF的距离为AC=,S△BEF=EF×BB1=,所以VA-BEF=××=为定值,C正确,故选D.
二、填空题(每小题5分,共15分)
9.已知直线a∥平面α,平面α∥平面β,则直线a与β的位置关系为________.
答案:a∥β或a?β
10.一个几何体的三视图如图所示,其中主视图和左视图均为腰长为2的等腰直角三角形,则用________个这样的几何体可以拼成一个棱长为2的正方体.
解析:正方体的体积V正方体=2×2×2=8,由三视图可知该几何体是四棱锥,V=×2×2×2=,故用3个这样的几何体可以拼成一个棱长为2的正方体.
答案:3
11.如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是________cm2.
解析:由三视图可知,该几何体是由正四棱锥和正方体组成,四棱锥的底面为正方形,边长为2,高为1,则斜高为=,正方体的棱长为2,S表=×2××4+2×2×5=4+20.
答案:20+4
三、解答题(每小题15分,共45分)
12.(2018·全国卷Ⅰ)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°,以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.
(1)证明:平面ACD⊥平面ABC;
(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ=DA,求三棱锥Q-ABP的体积.
解:(1)证明:由已知可得,∠BAC=90°,BA⊥AC.
又BA⊥AD且AC∩AD=A,所以AB⊥平面ACD.
又AB?平面ABC,
所以平面ACD⊥平面ABC.
(2)由已知可得,DC=CM=AB=3,DA=3.
又BP=DQ=DA,所以BP=2.
作QE⊥AC,垂足为E,则QE綊DC.
由已知及(1)可得DC⊥平面ABC,所以QE⊥平面ABC,且QE=1.
因此,三棱锥Q-ABP的体积为
VQ-ABP=×QE×S△ABP=×1××3×2sin45°=1.
13.如图(1)矩形ABCD中,AB=2AD=2a,E为DC的中点,现将△ADE沿AE折起,使平面ADE⊥平面ABCE,如图(2).
(1)求四棱锥D-ABCE的体积;
(2)求证:AD⊥平面BDE.
解:(1)∵平面ADE⊥平面ABCE,AD=DE,取AE的中点M,则DM⊥底面ABCE.
∴VD-ABCE=×DM·SABCE=×a××a=a3.
(2)证明:在△ABE中,AE=a,BE=a,
∴AE2+EB2=AB2.
∴BE⊥AE,又平面ADE⊥平面ABE,
∴BE⊥平面ADE,
∴BE⊥AD,又AD⊥DE,
∴AD⊥平面BDE.
14.如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,记CD=x,V(x)表示四棱锥F-ABCD的体积.
(1)求V(x)的表达式;
(2)求V(x)的最大值.
解:(1)∵平面ADEF⊥平面ABCD,交线为AD且FA⊥AD,
∴FA⊥平面ABCD.
∵BD⊥CD,BC=2,CD=x,
∴FA=2,BD=(0<x<2),
∴S?ABCD=CD·BD=x,
∴V(x)=S?ABCD·FA=x(0<x<2).
(2)V(x)=x=
=
.
∵0<x<2,∴0<x2<4,
∴当x2=2,
即x=时,V(x)取得最大值,且V(x)max=.
末
检
测
(时间:60分钟
满分:100分)
一、选择题(每小题5分,共40分)
1.设直线m,n和平面α,β,下列四个命题中,正确的是( )
A.若m∥α,n∥α,则m∥n
B.m?α,n?α,m∥β,n∥β,则α∥β
C.若α⊥β,m?α,则m⊥β
D.α⊥β,m⊥β,m?α,则m∥α
2.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的主视图(等腰直角三角形)和左视图,且该几何体的体积为,则该几何体的俯视图可以是( )
3.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题正确的是( )
A.若m⊥n,m⊥α,n∥β,则α∥β
B.若m∥n,m∥α,n∥β,则α∥β
C.若m⊥α,n∥β,α∥β,则m⊥n
D.若m∥α,n∥β,α∥β,则m∥n
4.某三棱锥的三视图如图所示,则该三棱锥的体积是( )
A.
B.
C.
D.1
5.某三棱锥的三视图如图所示,三个三角形均为直角三角形,则xy的最大值为( )
A.32
B.64
C.32
D.64
6.在三棱锥S-ABC中,SA⊥平面ABC,SA=2,△ABC是边长为1的正三角形,则其外接球的表面积为( )
A.
B.
C.
D.π
7.(2017·全国卷Ⅲ)在正方体ABCD-A1B1C1D1中,E为棱CD的中点,则( )
A.A1E⊥DC1
B.A1E⊥BD
C.A1E⊥BC1
D.A1E⊥AC
8.如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=,则下列结论中错误的是( )
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值
D.△AEF的面积与△BEF的面积相等
二、填空题(每小题5分,共15分)
9.已知直线a∥平面α,平面α∥平面β,则直线a与β的位置关系为________.
10.一个几何体的三视图如图所示,其中主视图和左视图均为腰长为2的等腰直角三角形,则用________个这样的几何体可以拼成一个棱长为2的正方体.
11.如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是________cm2.
三、解答题(每小题15分,共45分)
12.(2018·全国卷Ⅰ)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°,以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.
(1)证明:平面ACD⊥平面ABC;
(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ=DA,求三棱锥Q-ABP的体积.
13.如图(1)矩形ABCD中,AB=2AD=2a,E为DC的中点,现将△ADE沿AE折起,使平面ADE⊥平面ABCE,如图(2).
(1)求四棱锥D-ABCE的体积;
(2)求证:AD⊥平面BDE.
14.如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,记CD=x,V(x)表示四棱锥F-ABCD的体积.
(1)求V(x)的表达式;
(2)求V(x)的最大值.
第一章章
末
检
测
(时间:60分钟
满分:100分)
一、选择题(每小题5分,共40分)
1.设直线m,n和平面α,β,下列四个命题中,正确的是( )
A.若m∥α,n∥α,则m∥n
B.m?α,n?α,m∥β,n∥β,则α∥β
C.若α⊥β,m?α,则m⊥β
D.α⊥β,m⊥β,m?α,则m∥α
答案:D
2.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的主视图(等腰直角三角形)和左视图,且该几何体的体积为,则该几何体的俯视图可以是( )
解析:D 如图所示,将几何体放入正方体内,正方体的棱长为2,体积为8,当俯视图为是D选项时,该几何体是四棱锥E-ABCD,VE-ABCD=×2×2×2=,符合题意,故选D.
3.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题正确的是( )
A.若m⊥n,m⊥α,n∥β,则α∥β
B.若m∥n,m∥α,n∥β,则α∥β
C.若m⊥α,n∥β,α∥β,则m⊥n
D.若m∥α,n∥β,α∥β,则m∥n
解析:C C中由m⊥α,α∥β,可知m⊥β,又n∥β,∴m⊥n,故C正确.
4.某三棱锥的三视图如图所示,则该三棱锥的体积是( )
A.
B.
C.
D.1
解析:B 由三视图可知三棱锥的底面为等腰直角三角形,高为2,则V=××1×1×2=,故选B.
5.某三棱锥的三视图如图所示,三个三角形均为直角三角形,则xy的最大值为( )
A.32
B.64
C.32
D.64
解析:B 设该几何体的高为h,则
∴x2y2=(102-h2)(28+h2)=-h4+72h2+280,∴h2=36时,xy的最大值为64,故选B.
6.在三棱锥S-ABC中,SA⊥平面ABC,SA=2,△ABC是边长为1的正三角形,则其外接球的表面积为( )
A.
B.
C.
D.π
解析:B ∵△ABC为正三角形,
∴△ABC的外接圆的半径为××1=.
设外接球的半径为R,
则R2=2+2=.
∴S球=4πR2=.故选B.
7.(2017·全国卷Ⅲ)在正方体ABCD-A1B1C1D1中,E为棱CD的中点,则( )
A.A1E⊥DC1
B.A1E⊥BD
C.A1E⊥BC1
D.A1E⊥AC
解析:C 由正方体的性质,得A1B1⊥BC1,B1C⊥BC1,所以BC1⊥平面A1B1CD,又A1E?平面A1B1CD,所以A1E⊥BC1,故选C.
8.如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=,则下列结论中错误的是( )
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值
D.△AEF的面积与△BEF的面积相等
解析:D ∵AC⊥BD,BB1⊥底面ABCD,∴BB1⊥AC,∴AC⊥平面B1D1D,BE?面BDD1B1,∴AC⊥BE,A正确;∵EF∥BD,∴EF∥平面ABCD,B正确;A到平面BEF的距离为AC=,S△BEF=EF×BB1=,所以VA-BEF=××=为定值,C正确,故选D.
二、填空题(每小题5分,共15分)
9.已知直线a∥平面α,平面α∥平面β,则直线a与β的位置关系为________.
答案:a∥β或a?β
10.一个几何体的三视图如图所示,其中主视图和左视图均为腰长为2的等腰直角三角形,则用________个这样的几何体可以拼成一个棱长为2的正方体.
解析:正方体的体积V正方体=2×2×2=8,由三视图可知该几何体是四棱锥,V=×2×2×2=,故用3个这样的几何体可以拼成一个棱长为2的正方体.
答案:3
11.如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是________cm2.
解析:由三视图可知,该几何体是由正四棱锥和正方体组成,四棱锥的底面为正方形,边长为2,高为1,则斜高为=,正方体的棱长为2,S表=×2××4+2×2×5=4+20.
答案:20+4
三、解答题(每小题15分,共45分)
12.(2018·全国卷Ⅰ)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°,以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.
(1)证明:平面ACD⊥平面ABC;
(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ=DA,求三棱锥Q-ABP的体积.
解:(1)证明:由已知可得,∠BAC=90°,BA⊥AC.
又BA⊥AD且AC∩AD=A,所以AB⊥平面ACD.
又AB?平面ABC,
所以平面ACD⊥平面ABC.
(2)由已知可得,DC=CM=AB=3,DA=3.
又BP=DQ=DA,所以BP=2.
作QE⊥AC,垂足为E,则QE綊DC.
由已知及(1)可得DC⊥平面ABC,所以QE⊥平面ABC,且QE=1.
因此,三棱锥Q-ABP的体积为
VQ-ABP=×QE×S△ABP=×1××3×2sin45°=1.
13.如图(1)矩形ABCD中,AB=2AD=2a,E为DC的中点,现将△ADE沿AE折起,使平面ADE⊥平面ABCE,如图(2).
(1)求四棱锥D-ABCE的体积;
(2)求证:AD⊥平面BDE.
解:(1)∵平面ADE⊥平面ABCE,AD=DE,取AE的中点M,则DM⊥底面ABCE.
∴VD-ABCE=×DM·SABCE=×a××a=a3.
(2)证明:在△ABE中,AE=a,BE=a,
∴AE2+EB2=AB2.
∴BE⊥AE,又平面ADE⊥平面ABE,
∴BE⊥平面ADE,
∴BE⊥AD,又AD⊥DE,
∴AD⊥平面BDE.
14.如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,记CD=x,V(x)表示四棱锥F-ABCD的体积.
(1)求V(x)的表达式;
(2)求V(x)的最大值.
解:(1)∵平面ADEF⊥平面ABCD,交线为AD且FA⊥AD,
∴FA⊥平面ABCD.
∵BD⊥CD,BC=2,CD=x,
∴FA=2,BD=(0<x<2),
∴S?ABCD=CD·BD=x,
∴V(x)=S?ABCD·FA=x(0<x<2).
(2)V(x)=x=
=
.
∵0<x<2,∴0<x2<4,
∴当x2=2,
即x=时,V(x)取得最大值,且V(x)max=.
