人教B版数学必修二第一章立体几何初步章末检测卷 word版含解析解析
文档属性
| 名称 | 人教B版数学必修二第一章立体几何初步章末检测卷 word版含解析解析 |  | |
| 格式 | zip | ||
| 文件大小 | 472.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-16 21:22:43 | ||
图片预览


文档简介
(第一章 立体几何初步)
时间:120分钟 满分:150分
一、选择题(本大题共12小题,每小题5分,共60分)
1.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
A.若α⊥β,m?α,n?β,则m⊥n
B.若α∥β,m?α,n?β,则m∥n
C.若m⊥n,m?α,n?β,则α⊥β
D.若m⊥α,m∥n,n∥β,则α⊥β
2.若直线l不平行于平面α,且l?α,则( )
A.α与直线l至少有两个公共点
B.α内的直线与l都相交
C.α内的所有直线与l异面
D.α内不存在与l平行的直线
3.利用斜二测画法画平面内一个三角形的直观图得到的图形还是一个三角形,那么直观图三角形的面积与原来三角形面积的比是( )
A.
B.
C.
D.
4.球的体积与其表面积的数值相等,则球的半径等于( )
A.
B.1
C.2
D.3
5.下列命题中正确的是( )
A.若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点
B.若直线l与平面α平行,则l与平面α内的任意一条直线都平行
C.若直线l上有无数个点不在平面α内,则l∥α
D.如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行
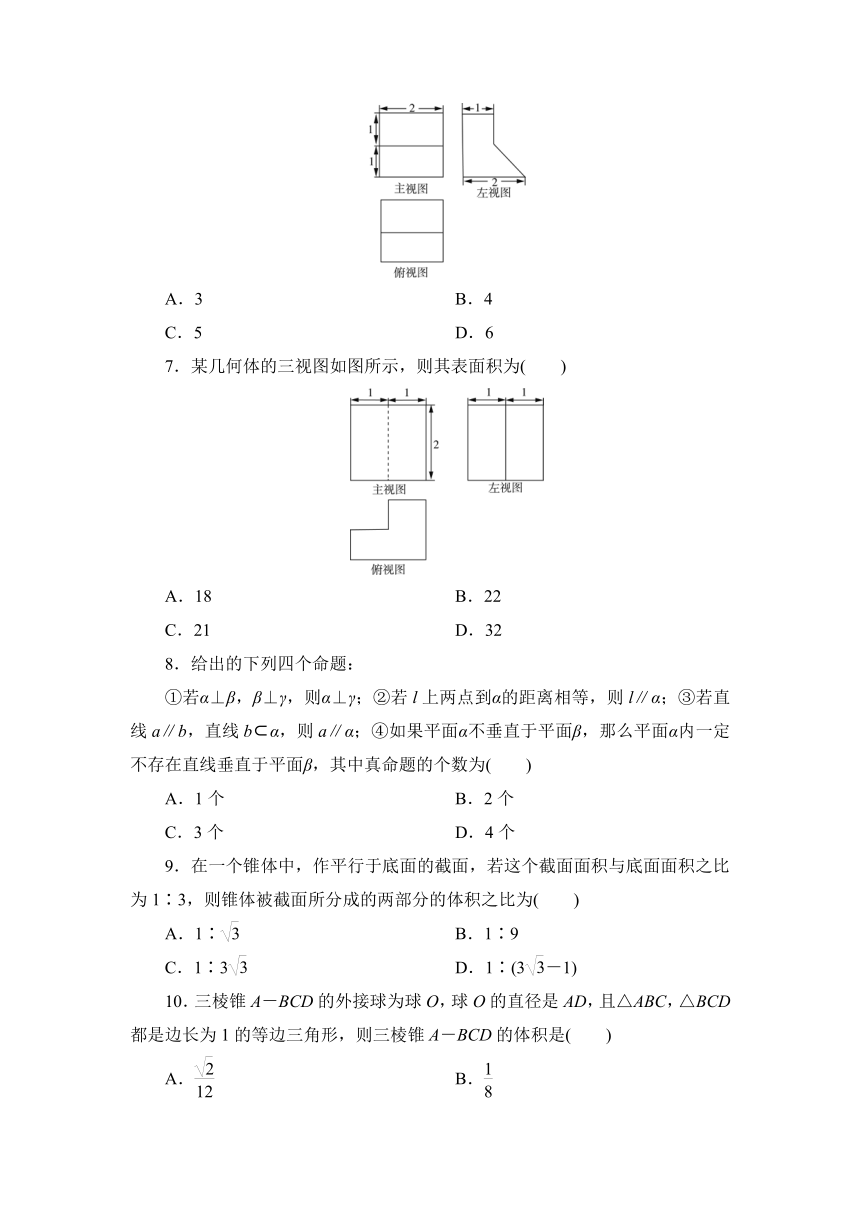
6.一个几何体的三视图如图所示,则该几何体的体积为( )
A.3
B.4
C.5
D.6
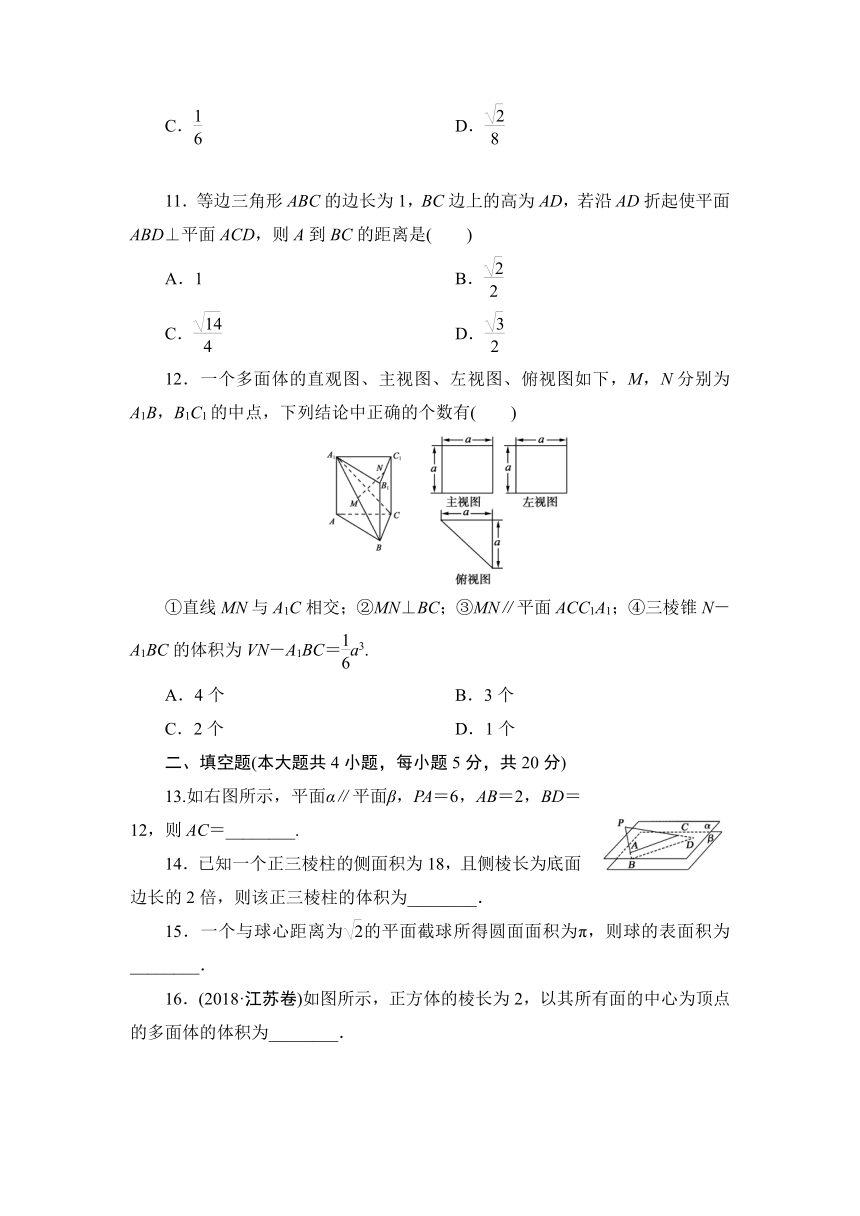
7.某几何体的三视图如图所示,则其表面积为( )
A.18
B.22
C.21
D.32
8.给出的下列四个命题:
①若α⊥β,β⊥γ,则α⊥γ;②若l上两点到α的距离相等,则l∥α;③若直线a∥b,直线b?α,则a∥α;④如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β,其中真命题的个数为( )
A.1个
B.2个
C.3个
D.4个
9.在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为( )
A.1∶
B.1∶9
C.1∶3
D.1∶(3-1)
10.三棱锥A-BCD的外接球为球O,球O的直径是AD,且△ABC,△BCD都是边长为1的等边三角形,则三棱锥A-BCD的体积是( )
A.
B.
C.
D.
11.等边三角形ABC的边长为1,BC边上的高为AD,若沿AD折起使平面ABD⊥平面ACD,则A到BC的距离是( )
A.1
B.
C.
D.
12.一个多面体的直观图、主视图、左视图、俯视图如下,M,N分别为A1B,B1C1的中点,下列结论中正确的个数有( )
①直线MN与A1C相交;②MN⊥BC;③MN∥平面ACC1A1;④三棱锥N-A1BC的体积为VN-A1BC=a3.
A.4个
B.3个
C.2个
D.1个
二、填空题(本大题共4小题,每小题5分,共20分)
13.如右图所示,平面α∥平面β,PA=6,AB=2,BD=12,则AC=________.
14.已知一个正三棱柱的侧面积为18,且侧棱长为底面边长的2倍,则该正三棱柱的体积为________.
15.一个与球心距离为的平面截球所得圆面面积为π,则球的表面积为________.
16.(2018·江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.
三、解答题(本大题共6小题,共70分)
17.(10分)如图,在四棱锥P-ABCD中,M为AD的中点.
(1)若AD∥BC,AD=2BC,求证:BM∥平面PCD;
(2)若PA=PD,平面PAD⊥平面PBM,求证:AD⊥PB.
18.(12分)如图所示,已知ABCD是矩形,E是以DC为直径的半圆周上一点,且平面CDE⊥平面ABCD.
求证:CE⊥平面ADE.
19.(12分)已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4,求四棱锥F-ABCD的体积.
20.(12分)如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=.
(1)证明:平面A1BD∥平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
21.(12分)如图所示,在正三棱柱(底面是正三角形,侧棱和底面垂直的三棱柱)ABC-A1B1C1中,AB=AA1,D是BC上的一点,且AD⊥C1D.
(1)求证:A1B∥平面AC1D;
(2)在棱CC1上是否存在一点P,使直线PB1⊥平面AC1D?若存在,找出这个点,并加以证明;若不存在,请说明理由.
22.(12分)如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
(1)求证:平面FGH∥平面PDE;
(2)求证:平面FGH⊥平面AEB;
(3)在线段PC上是否存在一点M,使PB⊥平面EFM?若存在,求出线段PM的长;若不存在,请说明理由.
(第一章 立体几何初步)
时间:120分钟 满分:150分
一、选择题(本大题共12小题,每小题5分,共60分)
1.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
A.若α⊥β,m?α,n?β,则m⊥n
B.若α∥β,m?α,n?β,则m∥n
C.若m⊥n,m?α,n?β,则α⊥β
D.若m⊥α,m∥n,n∥β,则α⊥β
解析:D ∵m⊥α,m∥n,∴n⊥α,又n∥β,∴β内存在n′∥n,∴n′⊥α,∴α⊥β,故选D.
2.若直线l不平行于平面α,且l?α,则( )
A.α与直线l至少有两个公共点
B.α内的直线与l都相交
C.α内的所有直线与l异面
D.α内不存在与l平行的直线
答案:D
3.利用斜二测画法画平面内一个三角形的直观图得到的图形还是一个三角形,那么直观图三角形的面积与原来三角形面积的比是( )
A.
B.
C.
D.
解析:A S原=a·h,S直=a··=·ah=S原,∴=,故选A.
4.球的体积与其表面积的数值相等,则球的半径等于( )
A.
B.1
C.2
D.3
解析:D 由题可得,πR3=4πR2,
∴R=3,故选D.
5.下列命题中正确的是( )
A.若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点
B.若直线l与平面α平行,则l与平面α内的任意一条直线都平行
C.若直线l上有无数个点不在平面α内,则l∥α
D.如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行
答案:A
6.一个几何体的三视图如图所示,则该几何体的体积为( )
A.3
B.4
C.5
D.6
解析:C 从题设所提供的三视图中的图形信息与数据信息可知该几何体是底面分别是矩形与梯形且等高的两个棱柱的组合体,V=1×1+×1×2=5,故选C.
7.某几何体的三视图如图所示,则其表面积为( )
A.18
B.22
C.21
D.32
解析:B 由三视图可知,该几何体是一个正方体挖掉一部分构成,如图所示:S=2×2×4+(1×1+2×1)×2=22,故选B.
8.给出的下列四个命题:
①若α⊥β,β⊥γ,则α⊥γ;②若l上两点到α的距离相等,则l∥α;③若直线a∥b,直线b?α,则a∥α;④如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β,其中真命题的个数为( )
A.1个
B.2个
C.3个
D.4个
解析:A ①中α与γ可能相交,可能平行,①错;②中l与α可能相交,②错;③中a?α有可能成立,③错;④正确,故选A.
9.在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为( )
A.1∶
B.1∶9
C.1∶3
D.1∶(3-1)
解析:D 由截面面积与底面面积之比为1∶3,则截得的锥体与原锥体的体积比为1∶3,则截得的两部分的体积之比为1∶(3-1),故选D.
10.三棱锥A-BCD的外接球为球O,球O的直径是AD,且△ABC,△BCD都是边长为1的等边三角形,则三棱锥A-BCD的体积是( )
A.
B.
C.
D.
解析:A 如图所示,由题可知球心O为AD的中点,
取BC的中点为E,连接AE,ED,因为△ABC,△BCD都是边长为1的等边三角形,所以AE⊥BC,DE⊥BC,所以BC⊥平面AED,AE=ED=,AD为直径,
所以∠ABD=90°,
∴AD==,
∴EO==
=.
∴VA-BCD=BC·S△AED=×1××AD×EO=××=,故选A.
11.等边三角形ABC的边长为1,BC边上的高为AD,若沿AD折起使平面ABD⊥平面ACD,则A到BC的距离是( )
A.1
B.
C.
D.
解析:C ∵△ABC为等边三角形,∴D为BC的中点,
∴BD=DC=,AB=AC=1.在Rt△BDC中,BC=.过点A作AH⊥BC于H,则H为BC的中点,
∴BH=,在Rt△ABH中,AH===.故选C.
12.一个多面体的直观图、主视图、左视图、俯视图如下,M,N分别为A1B,B1C1的中点,下列结论中正确的个数有( )
①直线MN与A1C相交;②MN⊥BC;③MN∥平面ACC1A1;④三棱锥N-A1BC的体积为VN-A1BC=a3.
A.4个
B.3个
C.2个
D.1个
解析:B 由三视图可知,其直观图为直三棱柱,AC⊥BC,且AC=BC=a,AA1=a,∴VN-A1BC=VA1-NBC=××a2×a=,故④正确,
连接AB1,则M在AB1上且M为AB1的中点,又N为B1C1的中点,∴MN∥AC1,
又AC1?平面ACC1A,MN?平面ACC1A1,
∴MN∥平面ACC1A1,故③正确.又A1C1CA为正方形,
∴A1C⊥AC1,∴MN⊥A1C,
∵A1N= =a,
BN= =a,
∴A1N=BN,∴MN⊥A1B,∴MN⊥平面A1BC,∴MN⊥BC,故②正确,①中MN与A1C异面,故①不正确.
二、填空题(本大题共4小题,每小题5分,共20分)
13.如右图所示,平面α∥平面β,PA=6,AB=2,BD=12,则AC=________.
解析:==,可解得AC=9.
答案:9
14.已知一个正三棱柱的侧面积为18,且侧棱长为底面边长的2倍,则该正三棱柱的体积为________.
解析:设正三棱柱的底面边长为a,
由题可知,3×a·2a=18,
∴a2=3,∴a=,V=××××2=.
答案:
15.一个与球心距离为的平面截球所得圆面面积为π,则球的表面积为________.
解析:截面圆的面积为π,则半径r=1,
所以球的半径为R==,
所以S球=4πR2=12π.
答案:12π
16.(2018·江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.
解析:由图可知,该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正方形的边长等于,所以该多面体的体积为2××1×()2=.
答案:
三、解答题(本大题共6小题,共70分)
17.(10分)如图,在四棱锥P-ABCD中,M为AD的中点.
(1)若AD∥BC,AD=2BC,求证:BM∥平面PCD;
(2)若PA=PD,平面PAD⊥平面PBM,求证:AD⊥PB.
证明:(1)∵AD∥BC,AD=2BC,
∴MD綊BC,
∴四边形BCDM是平行四边形,
∴BM∥CD,又BM?平面PCD,CD?平面PCD,
∴BM∥平面PCD.
(2)∵PA=PD,M是AD的中点,
∴PM⊥AD,
又平面PAD⊥平面PBM,
∴AD⊥平面PBM,
∴AD⊥PB.
18.(12分)如图所示,已知ABCD是矩形,E是以DC为直径的半圆周上一点,且平面CDE⊥平面ABCD.
求证:CE⊥平面ADE.
证明:∵E是以DC为直径的半圆周上一点,
∴CE⊥DE,
又∵平面CDE⊥平面ABCD,且AD⊥DC,
∴AD⊥平面CDE,又CE?面CDE,
∴AD⊥CE.又∵DE∩AD=D,
∴CE⊥平面ADE.
19.(12分)已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4,求四棱锥F-ABCD的体积.
解:(1)证明:∵EF∥AD,AD∥BC,∴EF∥BC且EF=AD=BC,
∴四边形EFBC是平行四边形,
∴H为FC的中点.
又∵G是FD的中点,∴HG∥CD.
∵HG?平面CDE,CD?平面CDE,
∴GH∥平面CDE.
(2)∵平面ADEF⊥平面ABCD,交线为AD且FA⊥AD,∴FA⊥平面ABCD.
∵BC=6,∴FA=6.
又∵CD=2,DB=4,CD2+DB2=BC2,
∴BD⊥CD,
∴SABCD=CD×BD=8,
∴VF-ABCD=×SABCD×FA=×8×6=16.
20.(12分)如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=.
(1)证明:平面A1BD∥平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
解:(1)证明:由题知,BB1綊DD1,∴BB1D1D是平行四边形,
∴BD∥B1D1,
又BD?平面CD1B1,∴BD∥平面CD1B1.
∵A1D1綊B1C1綊BC,
∴A1BCD1是平行四边形,
∴A1B∥D1C,
又∵A1B?平面CD1B1
∴A1B∥平面CD1B1,
∵A1B∩BD=B,
∴平面A1BD∥平面CD1B1
(2)∵A1O⊥平面ABCD,
∴A1O是三棱柱ABD-A1B1D1的高.
又∵AO=AC=1,AA1=,
∴A1O=1.又∵S△ABD=××=1,
∴V=S△ABD×A1O=1.
21.(12分)如图所示,在正三棱柱(底面是正三角形,侧棱和底面垂直的三棱柱)ABC-A1B1C1中,AB=AA1,D是BC上的一点,且AD⊥C1D.
(1)求证:A1B∥平面AC1D;
(2)在棱CC1上是否存在一点P,使直线PB1⊥平面AC1D?若存在,找出这个点,并加以证明;若不存在,请说明理由.
解:(1)证明:∵三棱柱ABC-A1B1C1是正三棱柱,
∴CC1⊥平面ABC,
∴CC1⊥AD.
又AD⊥C1D,CC1∩C1D=C1,
∴AD⊥平面BCC1B1,
∴AD⊥BC,∴D是BC的中点.
连接A1C,设与AC1相交于点E,则点E为A1C的中点.
连接DE,则在△A1BC中,
∵D、E分别是BC、A1C的中点,∴A1B∥DE.
又DE在平面AC1D内,A1B不在平面AC1D内,
∴A1B∥平面AC1D.
(2)存在这样的点P,且点P为CC1的中点.证明如下:由(1)知AD⊥平面BCC1B1,故B1P⊥AD.
设PB1与C1D相交于点Q,由于△DC1C≌△PB1C1,
故∠QB1C1=∠CC1D,
因为∠QC1B1=∠CDC1,从而△QC1B1∽△CDC1,
所以∠C1QB1=∠DCC1=90°,所以B1P⊥C1D.
因为AD∩C1D=D,所以B1P⊥平面AC1D.
22.(12分)如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
(1)求证:平面FGH∥平面PDE;
(2)求证:平面FGH⊥平面AEB;
(3)在线段PC上是否存在一点M,使PB⊥平面EFM?若存在,求出线段PM的长;若不存在,请说明理由.
解:(1)证明:因为F,G分别为BP,BE的中点,
所以FG∥PE.
又因为FG?平面PED,PE?平面PED,
所以FG∥平面PED,同理FH∥BC,
又BC∥AD,所以FH∥平面PDE
而FG∩FH=F,故平面FGH∥平面PDE.
(2)证明:因为EA⊥平面ABCD,所以EA⊥CB.
又因为CB⊥AB,AB∩AE=A,所以CB⊥平面AEB.
由已知F,H分别为线段PB,PC的中点,所以FH∥BC,则FH⊥平面AEB.
而FH?平面FGH,所以平面FGH⊥平面AEB.
(3)在线段PC上存在一点M,使PB⊥平面EFM.
证明如下:在直角三角形AEB中,因为AE=1,AB=2,所以BE=.在直角梯形EADP中,
因为AE=1,AD=PD=2,所以PE=,所以PE=BE.
又因为F为PB的中点,所以EF⊥PB.要使PB⊥平面EFM,只需使PB⊥FM.
因为PD⊥平面ABCD,所以PD⊥CB,
又因为CB⊥CD,PD∩CD=D,所以CB⊥平面PCD,而PC?平面PCD,所以CB⊥PC.
若PB⊥FM,则△PFM∽△PCB,可得PM∶PB=PF∶PC.
由已知可求得PB=2,PF=,PC=2,所以PM=.
时间:120分钟 满分:150分
一、选择题(本大题共12小题,每小题5分,共60分)
1.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
A.若α⊥β,m?α,n?β,则m⊥n
B.若α∥β,m?α,n?β,则m∥n
C.若m⊥n,m?α,n?β,则α⊥β
D.若m⊥α,m∥n,n∥β,则α⊥β
2.若直线l不平行于平面α,且l?α,则( )
A.α与直线l至少有两个公共点
B.α内的直线与l都相交
C.α内的所有直线与l异面
D.α内不存在与l平行的直线
3.利用斜二测画法画平面内一个三角形的直观图得到的图形还是一个三角形,那么直观图三角形的面积与原来三角形面积的比是( )
A.
B.
C.
D.
4.球的体积与其表面积的数值相等,则球的半径等于( )
A.
B.1
C.2
D.3
5.下列命题中正确的是( )
A.若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点
B.若直线l与平面α平行,则l与平面α内的任意一条直线都平行
C.若直线l上有无数个点不在平面α内,则l∥α
D.如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行
6.一个几何体的三视图如图所示,则该几何体的体积为( )
A.3
B.4
C.5
D.6
7.某几何体的三视图如图所示,则其表面积为( )
A.18
B.22
C.21
D.32
8.给出的下列四个命题:
①若α⊥β,β⊥γ,则α⊥γ;②若l上两点到α的距离相等,则l∥α;③若直线a∥b,直线b?α,则a∥α;④如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β,其中真命题的个数为( )
A.1个
B.2个
C.3个
D.4个
9.在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为( )
A.1∶
B.1∶9
C.1∶3
D.1∶(3-1)
10.三棱锥A-BCD的外接球为球O,球O的直径是AD,且△ABC,△BCD都是边长为1的等边三角形,则三棱锥A-BCD的体积是( )
A.
B.
C.
D.
11.等边三角形ABC的边长为1,BC边上的高为AD,若沿AD折起使平面ABD⊥平面ACD,则A到BC的距离是( )
A.1
B.
C.
D.
12.一个多面体的直观图、主视图、左视图、俯视图如下,M,N分别为A1B,B1C1的中点,下列结论中正确的个数有( )
①直线MN与A1C相交;②MN⊥BC;③MN∥平面ACC1A1;④三棱锥N-A1BC的体积为VN-A1BC=a3.
A.4个
B.3个
C.2个
D.1个
二、填空题(本大题共4小题,每小题5分,共20分)
13.如右图所示,平面α∥平面β,PA=6,AB=2,BD=12,则AC=________.
14.已知一个正三棱柱的侧面积为18,且侧棱长为底面边长的2倍,则该正三棱柱的体积为________.
15.一个与球心距离为的平面截球所得圆面面积为π,则球的表面积为________.
16.(2018·江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.
三、解答题(本大题共6小题,共70分)
17.(10分)如图,在四棱锥P-ABCD中,M为AD的中点.
(1)若AD∥BC,AD=2BC,求证:BM∥平面PCD;
(2)若PA=PD,平面PAD⊥平面PBM,求证:AD⊥PB.
18.(12分)如图所示,已知ABCD是矩形,E是以DC为直径的半圆周上一点,且平面CDE⊥平面ABCD.
求证:CE⊥平面ADE.
19.(12分)已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4,求四棱锥F-ABCD的体积.
20.(12分)如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=.
(1)证明:平面A1BD∥平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
21.(12分)如图所示,在正三棱柱(底面是正三角形,侧棱和底面垂直的三棱柱)ABC-A1B1C1中,AB=AA1,D是BC上的一点,且AD⊥C1D.
(1)求证:A1B∥平面AC1D;
(2)在棱CC1上是否存在一点P,使直线PB1⊥平面AC1D?若存在,找出这个点,并加以证明;若不存在,请说明理由.
22.(12分)如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
(1)求证:平面FGH∥平面PDE;
(2)求证:平面FGH⊥平面AEB;
(3)在线段PC上是否存在一点M,使PB⊥平面EFM?若存在,求出线段PM的长;若不存在,请说明理由.
(第一章 立体几何初步)
时间:120分钟 满分:150分
一、选择题(本大题共12小题,每小题5分,共60分)
1.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
A.若α⊥β,m?α,n?β,则m⊥n
B.若α∥β,m?α,n?β,则m∥n
C.若m⊥n,m?α,n?β,则α⊥β
D.若m⊥α,m∥n,n∥β,则α⊥β
解析:D ∵m⊥α,m∥n,∴n⊥α,又n∥β,∴β内存在n′∥n,∴n′⊥α,∴α⊥β,故选D.
2.若直线l不平行于平面α,且l?α,则( )
A.α与直线l至少有两个公共点
B.α内的直线与l都相交
C.α内的所有直线与l异面
D.α内不存在与l平行的直线
答案:D
3.利用斜二测画法画平面内一个三角形的直观图得到的图形还是一个三角形,那么直观图三角形的面积与原来三角形面积的比是( )
A.
B.
C.
D.
解析:A S原=a·h,S直=a··=·ah=S原,∴=,故选A.
4.球的体积与其表面积的数值相等,则球的半径等于( )
A.
B.1
C.2
D.3
解析:D 由题可得,πR3=4πR2,
∴R=3,故选D.
5.下列命题中正确的是( )
A.若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点
B.若直线l与平面α平行,则l与平面α内的任意一条直线都平行
C.若直线l上有无数个点不在平面α内,则l∥α
D.如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行
答案:A
6.一个几何体的三视图如图所示,则该几何体的体积为( )
A.3
B.4
C.5
D.6
解析:C 从题设所提供的三视图中的图形信息与数据信息可知该几何体是底面分别是矩形与梯形且等高的两个棱柱的组合体,V=1×1+×1×2=5,故选C.
7.某几何体的三视图如图所示,则其表面积为( )
A.18
B.22
C.21
D.32
解析:B 由三视图可知,该几何体是一个正方体挖掉一部分构成,如图所示:S=2×2×4+(1×1+2×1)×2=22,故选B.
8.给出的下列四个命题:
①若α⊥β,β⊥γ,则α⊥γ;②若l上两点到α的距离相等,则l∥α;③若直线a∥b,直线b?α,则a∥α;④如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β,其中真命题的个数为( )
A.1个
B.2个
C.3个
D.4个
解析:A ①中α与γ可能相交,可能平行,①错;②中l与α可能相交,②错;③中a?α有可能成立,③错;④正确,故选A.
9.在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为( )
A.1∶
B.1∶9
C.1∶3
D.1∶(3-1)
解析:D 由截面面积与底面面积之比为1∶3,则截得的锥体与原锥体的体积比为1∶3,则截得的两部分的体积之比为1∶(3-1),故选D.
10.三棱锥A-BCD的外接球为球O,球O的直径是AD,且△ABC,△BCD都是边长为1的等边三角形,则三棱锥A-BCD的体积是( )
A.
B.
C.
D.
解析:A 如图所示,由题可知球心O为AD的中点,
取BC的中点为E,连接AE,ED,因为△ABC,△BCD都是边长为1的等边三角形,所以AE⊥BC,DE⊥BC,所以BC⊥平面AED,AE=ED=,AD为直径,
所以∠ABD=90°,
∴AD==,
∴EO==
=.
∴VA-BCD=BC·S△AED=×1××AD×EO=××=,故选A.
11.等边三角形ABC的边长为1,BC边上的高为AD,若沿AD折起使平面ABD⊥平面ACD,则A到BC的距离是( )
A.1
B.
C.
D.
解析:C ∵△ABC为等边三角形,∴D为BC的中点,
∴BD=DC=,AB=AC=1.在Rt△BDC中,BC=.过点A作AH⊥BC于H,则H为BC的中点,
∴BH=,在Rt△ABH中,AH===.故选C.
12.一个多面体的直观图、主视图、左视图、俯视图如下,M,N分别为A1B,B1C1的中点,下列结论中正确的个数有( )
①直线MN与A1C相交;②MN⊥BC;③MN∥平面ACC1A1;④三棱锥N-A1BC的体积为VN-A1BC=a3.
A.4个
B.3个
C.2个
D.1个
解析:B 由三视图可知,其直观图为直三棱柱,AC⊥BC,且AC=BC=a,AA1=a,∴VN-A1BC=VA1-NBC=××a2×a=,故④正确,
连接AB1,则M在AB1上且M为AB1的中点,又N为B1C1的中点,∴MN∥AC1,
又AC1?平面ACC1A,MN?平面ACC1A1,
∴MN∥平面ACC1A1,故③正确.又A1C1CA为正方形,
∴A1C⊥AC1,∴MN⊥A1C,
∵A1N= =a,
BN= =a,
∴A1N=BN,∴MN⊥A1B,∴MN⊥平面A1BC,∴MN⊥BC,故②正确,①中MN与A1C异面,故①不正确.
二、填空题(本大题共4小题,每小题5分,共20分)
13.如右图所示,平面α∥平面β,PA=6,AB=2,BD=12,则AC=________.
解析:==,可解得AC=9.
答案:9
14.已知一个正三棱柱的侧面积为18,且侧棱长为底面边长的2倍,则该正三棱柱的体积为________.
解析:设正三棱柱的底面边长为a,
由题可知,3×a·2a=18,
∴a2=3,∴a=,V=××××2=.
答案:
15.一个与球心距离为的平面截球所得圆面面积为π,则球的表面积为________.
解析:截面圆的面积为π,则半径r=1,
所以球的半径为R==,
所以S球=4πR2=12π.
答案:12π
16.(2018·江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.
解析:由图可知,该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正方形的边长等于,所以该多面体的体积为2××1×()2=.
答案:
三、解答题(本大题共6小题,共70分)
17.(10分)如图,在四棱锥P-ABCD中,M为AD的中点.
(1)若AD∥BC,AD=2BC,求证:BM∥平面PCD;
(2)若PA=PD,平面PAD⊥平面PBM,求证:AD⊥PB.
证明:(1)∵AD∥BC,AD=2BC,
∴MD綊BC,
∴四边形BCDM是平行四边形,
∴BM∥CD,又BM?平面PCD,CD?平面PCD,
∴BM∥平面PCD.
(2)∵PA=PD,M是AD的中点,
∴PM⊥AD,
又平面PAD⊥平面PBM,
∴AD⊥平面PBM,
∴AD⊥PB.
18.(12分)如图所示,已知ABCD是矩形,E是以DC为直径的半圆周上一点,且平面CDE⊥平面ABCD.
求证:CE⊥平面ADE.
证明:∵E是以DC为直径的半圆周上一点,
∴CE⊥DE,
又∵平面CDE⊥平面ABCD,且AD⊥DC,
∴AD⊥平面CDE,又CE?面CDE,
∴AD⊥CE.又∵DE∩AD=D,
∴CE⊥平面ADE.
19.(12分)已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4,求四棱锥F-ABCD的体积.
解:(1)证明:∵EF∥AD,AD∥BC,∴EF∥BC且EF=AD=BC,
∴四边形EFBC是平行四边形,
∴H为FC的中点.
又∵G是FD的中点,∴HG∥CD.
∵HG?平面CDE,CD?平面CDE,
∴GH∥平面CDE.
(2)∵平面ADEF⊥平面ABCD,交线为AD且FA⊥AD,∴FA⊥平面ABCD.
∵BC=6,∴FA=6.
又∵CD=2,DB=4,CD2+DB2=BC2,
∴BD⊥CD,
∴SABCD=CD×BD=8,
∴VF-ABCD=×SABCD×FA=×8×6=16.
20.(12分)如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=.
(1)证明:平面A1BD∥平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
解:(1)证明:由题知,BB1綊DD1,∴BB1D1D是平行四边形,
∴BD∥B1D1,
又BD?平面CD1B1,∴BD∥平面CD1B1.
∵A1D1綊B1C1綊BC,
∴A1BCD1是平行四边形,
∴A1B∥D1C,
又∵A1B?平面CD1B1
∴A1B∥平面CD1B1,
∵A1B∩BD=B,
∴平面A1BD∥平面CD1B1
(2)∵A1O⊥平面ABCD,
∴A1O是三棱柱ABD-A1B1D1的高.
又∵AO=AC=1,AA1=,
∴A1O=1.又∵S△ABD=××=1,
∴V=S△ABD×A1O=1.
21.(12分)如图所示,在正三棱柱(底面是正三角形,侧棱和底面垂直的三棱柱)ABC-A1B1C1中,AB=AA1,D是BC上的一点,且AD⊥C1D.
(1)求证:A1B∥平面AC1D;
(2)在棱CC1上是否存在一点P,使直线PB1⊥平面AC1D?若存在,找出这个点,并加以证明;若不存在,请说明理由.
解:(1)证明:∵三棱柱ABC-A1B1C1是正三棱柱,
∴CC1⊥平面ABC,
∴CC1⊥AD.
又AD⊥C1D,CC1∩C1D=C1,
∴AD⊥平面BCC1B1,
∴AD⊥BC,∴D是BC的中点.
连接A1C,设与AC1相交于点E,则点E为A1C的中点.
连接DE,则在△A1BC中,
∵D、E分别是BC、A1C的中点,∴A1B∥DE.
又DE在平面AC1D内,A1B不在平面AC1D内,
∴A1B∥平面AC1D.
(2)存在这样的点P,且点P为CC1的中点.证明如下:由(1)知AD⊥平面BCC1B1,故B1P⊥AD.
设PB1与C1D相交于点Q,由于△DC1C≌△PB1C1,
故∠QB1C1=∠CC1D,
因为∠QC1B1=∠CDC1,从而△QC1B1∽△CDC1,
所以∠C1QB1=∠DCC1=90°,所以B1P⊥C1D.
因为AD∩C1D=D,所以B1P⊥平面AC1D.
22.(12分)如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
(1)求证:平面FGH∥平面PDE;
(2)求证:平面FGH⊥平面AEB;
(3)在线段PC上是否存在一点M,使PB⊥平面EFM?若存在,求出线段PM的长;若不存在,请说明理由.
解:(1)证明:因为F,G分别为BP,BE的中点,
所以FG∥PE.
又因为FG?平面PED,PE?平面PED,
所以FG∥平面PED,同理FH∥BC,
又BC∥AD,所以FH∥平面PDE
而FG∩FH=F,故平面FGH∥平面PDE.
(2)证明:因为EA⊥平面ABCD,所以EA⊥CB.
又因为CB⊥AB,AB∩AE=A,所以CB⊥平面AEB.
由已知F,H分别为线段PB,PC的中点,所以FH∥BC,则FH⊥平面AEB.
而FH?平面FGH,所以平面FGH⊥平面AEB.
(3)在线段PC上存在一点M,使PB⊥平面EFM.
证明如下:在直角三角形AEB中,因为AE=1,AB=2,所以BE=.在直角梯形EADP中,
因为AE=1,AD=PD=2,所以PE=,所以PE=BE.
又因为F为PB的中点,所以EF⊥PB.要使PB⊥平面EFM,只需使PB⊥FM.
因为PD⊥平面ABCD,所以PD⊥CB,
又因为CB⊥CD,PD∩CD=D,所以CB⊥平面PCD,而PC?平面PCD,所以CB⊥PC.
若PB⊥FM,则△PFM∽△PCB,可得PM∶PB=PF∶PC.
由已知可求得PB=2,PF=,PC=2,所以PM=.
