北师大版八年级数学下册: 6.1.1平行四边形性质 课件(共18张PPT)
文档属性
| 名称 | 北师大版八年级数学下册: 6.1.1平行四边形性质 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 423.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-15 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
北师大版八年级数学下册第六章6.1.1
平行四边形的性质(1)
1、掌握平行四边形的定义、表示方法及相关概念;
2、探索并掌握平行四边形的性质,并能简单应用.
一.学习目标
阅读课本135-136页,回答下列问题:
1、平行四边形的定义: 的四边形,叫做平行四边形。
2、平行四边形的表示:平行四边形用符号“______”表示。
3、平行四边形的不相邻的两个顶点连成的一条线段叫做它的 。
4.如图所示线段AC就是□ABCD的一条 .
两组对边分别平行
对角线
对角线
二.预习自测
1.平行四边形是中心对称图形吗?如果是,你能找到它的对称中心并验证你的结论吗?
平行四边形的性质1:
平行四边形是 中心对称图形,两条对角线的交点是它的对称中心
三.自主探究
2.平行四边形的对边、对角分别有什么关系?
平行四边形的性质2:平行四边形对边 ;
平行四边形的性质3:平行四边形对角 .
相等
相等
你能给出证明吗?
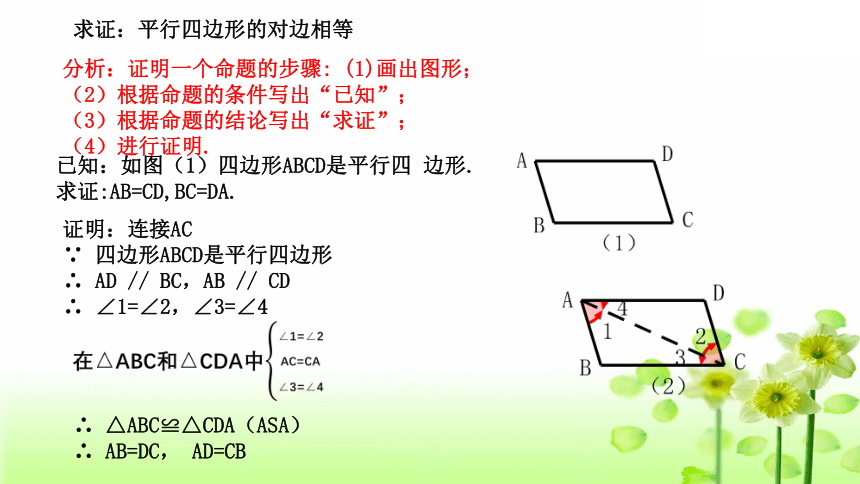
求证:平行四边形的对边相等
分析:证明一个命题的步骤: (1)画出图形;
(2)根据命题的条件写出“已知”;
(3)根据命题的结论写出“求证”;
(4)进行证明.
已知:如图(1)四边形ABCD是平行四 边形.
求证:AB=CD,BC=DA.
证明:连接AC
∵ 四边形ABCD是平行四边形
∴ AD // BC,AB // CD
∴ ∠1=∠2,∠3=∠4
∴ △ABC≌△CDA(ASA)
∴ AB=DC, AD=CB
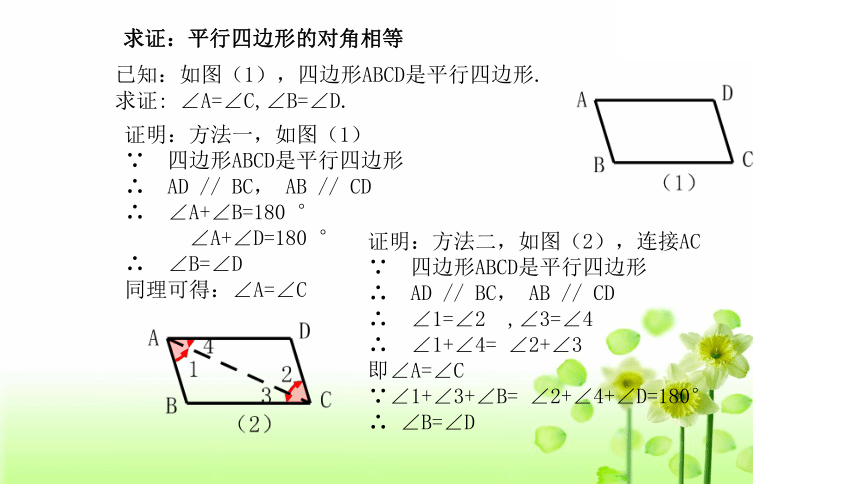
求证:平行四边形的对角相等
已知:如图(1),四边形ABCD是平行四边形.
求证: ∠A=∠C,∠B=∠D.
证明:方法一,如图(1)
∵ 四边形ABCD是平行四边形
∴ AD // BC, AB // CD
∴ ∠A+∠B=180 °
∠A+∠D=180 °
∴ ∠B=∠D
同理可得:∠A=∠C
证明:方法二,如图(2),连接AC
∵ 四边形ABCD是平行四边形
∴ AD // BC, AB // CD
∴ ∠1=∠2 ,∠3=∠4
∴ ∠1+∠4= ∠2+∠3
即∠A=∠C
∵∠1+∠3+∠B= ∠2+∠4+∠D=180°
∴ ∠B=∠D
3.平行四边形的性质用几何语言表示:
如图: ∵AD // BC ,
∴四边形ABCD是平行四边形;
∵ ABCD
∴ // , // ;
∵ ABCD
∴ = , = ;
∵ ABCD
∴ ∠ =∠ ,∠ =∠ ;
(1)平行四边形是 图形,对称中心是 ,
但不是 图形。
(2)平行四边形的 相等, 相等。
AB//CD
AB CD AD BC
A C B D
AB CD AD BC
中心对称
对角线的交点
轴对称
对边 对角
例1:四边形ABCD是平行四边形,AD=30,DC=25,∠B=56°
(1)求∠ADC和∠BCD的度数;
(2)求AB和BC的长度.
解: (1)∵四边形ABCD是平行四边形
∴ ∠ADC =∠B=56°,(平行四边形的对角相等)
AB // CD (平行四边形的对边平行)
∴∠B+∠BCD=180°
∴∠BCD =180°-56°=124°
(2)∵四边形ABCD是平行四边形
∴AB=DC=25,BC=AD=30(平行四边形的对边相等)
例2.已知:如图6-3,在平行四边形ABCD中,
E,F 是对角线AC上的两点,且AE=CF.
求证:BE = DF.
证明:∵四边形ABCD是平行四边形
∴AB = CD(平行四边形的对边相等)
AB // CD (平行四边形的定义)
∴∠BAE=∠DCF
又∵AE=CF
∴△BAE≌△DCF
∴BE=DF
四、随堂练习
1.填空(提示:下面的题都需自己先画出合适的平行四边形)
(1)在平行四边形ABCD中若∠B+∠D=80°,则∠A= ;∠C= 。
(2)若∠ABC=65°∠CAD=60°,则∠D= °;
∠ACD= °;∠BAC= °
140°
140°
65
55
55
2.如图,在平行四边形ABCD中,∠ADC=125°,∠CAD=21°,求∠ABD和∠CAB的度数。
解:在△ACD中,∠ADC=125°,∠CAD=21°
∴∠ACD=180°-125°-21°=34°
在平行四边形ABCD中,CD//AB
∴∠ABC=∠ADC=125°,∠CAB=∠ACD=34°
五,课堂小结
谈谈今天你有什么收获?
1.相关概念
(1)平行四边形的定义
(2)平行四边形对角线
(3)平行四边形ABCD记作
2.平行四边形性质
(1)平行四边形是 图形,对称中心是
(2)平行四边形的 相等, 相等。
五、当堂检测
1.在平行四边形ABCD中,周长为40cm,△ABC周长为25,则对角线AC= 。
2.在平行四边形ABCD中,周长为48cm,AB:BC=3:5,AD=_______,CD=______.
5
15 9
3.已知,如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,求证:BF=DE
证明:方法一,
在平行四边形ABCD中,AB//CD
∴∠AFD=∠CDF
∵DF是∠ADC的平分线 ∴∠ADF=∠CDF
∴∠AFD=∠ADF ∴AD=AF
同理CE=BC
∵AD=BC ∴AF=CE
∵AB=CD
∴DE=BF
3.已知,如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,求证:BF=DE
方法二,∵ABCD是平行四边形
∴∠ADC=∠ABC,AB∥CD
∴∠CDF=∠AFD
∵∠ABC平分线交CD于点E,∠ADC的平分线交AB于点F
∴∠CDF=1/2∠ADC,∠ABE=1/2∠ABC
∴∠CDF=∠ABE
∴∠AFD=∠ABE
∴DF∥BE
∵DE∥BF
∴BEDF是平行四边形
∴BF=DE
拓展提高题
1.易错题:未给出图形,需要进行分类讨论
在平行四边形ABCD中,AD=BD,BE是AD边上的高,∠EBD=20°,则∠A= .
55°或35°
A
北师大版八年级数学下册第六章6.1.1
平行四边形的性质(1)
1、掌握平行四边形的定义、表示方法及相关概念;
2、探索并掌握平行四边形的性质,并能简单应用.
一.学习目标
阅读课本135-136页,回答下列问题:
1、平行四边形的定义: 的四边形,叫做平行四边形。
2、平行四边形的表示:平行四边形用符号“______”表示。
3、平行四边形的不相邻的两个顶点连成的一条线段叫做它的 。
4.如图所示线段AC就是□ABCD的一条 .
两组对边分别平行
对角线
对角线
二.预习自测
1.平行四边形是中心对称图形吗?如果是,你能找到它的对称中心并验证你的结论吗?
平行四边形的性质1:
平行四边形是 中心对称图形,两条对角线的交点是它的对称中心
三.自主探究
2.平行四边形的对边、对角分别有什么关系?
平行四边形的性质2:平行四边形对边 ;
平行四边形的性质3:平行四边形对角 .
相等
相等
你能给出证明吗?
求证:平行四边形的对边相等
分析:证明一个命题的步骤: (1)画出图形;
(2)根据命题的条件写出“已知”;
(3)根据命题的结论写出“求证”;
(4)进行证明.
已知:如图(1)四边形ABCD是平行四 边形.
求证:AB=CD,BC=DA.
证明:连接AC
∵ 四边形ABCD是平行四边形
∴ AD // BC,AB // CD
∴ ∠1=∠2,∠3=∠4
∴ △ABC≌△CDA(ASA)
∴ AB=DC, AD=CB
求证:平行四边形的对角相等
已知:如图(1),四边形ABCD是平行四边形.
求证: ∠A=∠C,∠B=∠D.
证明:方法一,如图(1)
∵ 四边形ABCD是平行四边形
∴ AD // BC, AB // CD
∴ ∠A+∠B=180 °
∠A+∠D=180 °
∴ ∠B=∠D
同理可得:∠A=∠C
证明:方法二,如图(2),连接AC
∵ 四边形ABCD是平行四边形
∴ AD // BC, AB // CD
∴ ∠1=∠2 ,∠3=∠4
∴ ∠1+∠4= ∠2+∠3
即∠A=∠C
∵∠1+∠3+∠B= ∠2+∠4+∠D=180°
∴ ∠B=∠D
3.平行四边形的性质用几何语言表示:
如图: ∵AD // BC ,
∴四边形ABCD是平行四边形;
∵ ABCD
∴ // , // ;
∵ ABCD
∴ = , = ;
∵ ABCD
∴ ∠ =∠ ,∠ =∠ ;
(1)平行四边形是 图形,对称中心是 ,
但不是 图形。
(2)平行四边形的 相等, 相等。
AB//CD
AB CD AD BC
A C B D
AB CD AD BC
中心对称
对角线的交点
轴对称
对边 对角
例1:四边形ABCD是平行四边形,AD=30,DC=25,∠B=56°
(1)求∠ADC和∠BCD的度数;
(2)求AB和BC的长度.
解: (1)∵四边形ABCD是平行四边形
∴ ∠ADC =∠B=56°,(平行四边形的对角相等)
AB // CD (平行四边形的对边平行)
∴∠B+∠BCD=180°
∴∠BCD =180°-56°=124°
(2)∵四边形ABCD是平行四边形
∴AB=DC=25,BC=AD=30(平行四边形的对边相等)
例2.已知:如图6-3,在平行四边形ABCD中,
E,F 是对角线AC上的两点,且AE=CF.
求证:BE = DF.
证明:∵四边形ABCD是平行四边形
∴AB = CD(平行四边形的对边相等)
AB // CD (平行四边形的定义)
∴∠BAE=∠DCF
又∵AE=CF
∴△BAE≌△DCF
∴BE=DF
四、随堂练习
1.填空(提示:下面的题都需自己先画出合适的平行四边形)
(1)在平行四边形ABCD中若∠B+∠D=80°,则∠A= ;∠C= 。
(2)若∠ABC=65°∠CAD=60°,则∠D= °;
∠ACD= °;∠BAC= °
140°
140°
65
55
55
2.如图,在平行四边形ABCD中,∠ADC=125°,∠CAD=21°,求∠ABD和∠CAB的度数。
解:在△ACD中,∠ADC=125°,∠CAD=21°
∴∠ACD=180°-125°-21°=34°
在平行四边形ABCD中,CD//AB
∴∠ABC=∠ADC=125°,∠CAB=∠ACD=34°
五,课堂小结
谈谈今天你有什么收获?
1.相关概念
(1)平行四边形的定义
(2)平行四边形对角线
(3)平行四边形ABCD记作
2.平行四边形性质
(1)平行四边形是 图形,对称中心是
(2)平行四边形的 相等, 相等。
五、当堂检测
1.在平行四边形ABCD中,周长为40cm,△ABC周长为25,则对角线AC= 。
2.在平行四边形ABCD中,周长为48cm,AB:BC=3:5,AD=_______,CD=______.
5
15 9
3.已知,如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,求证:BF=DE
证明:方法一,
在平行四边形ABCD中,AB//CD
∴∠AFD=∠CDF
∵DF是∠ADC的平分线 ∴∠ADF=∠CDF
∴∠AFD=∠ADF ∴AD=AF
同理CE=BC
∵AD=BC ∴AF=CE
∵AB=CD
∴DE=BF
3.已知,如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,求证:BF=DE
方法二,∵ABCD是平行四边形
∴∠ADC=∠ABC,AB∥CD
∴∠CDF=∠AFD
∵∠ABC平分线交CD于点E,∠ADC的平分线交AB于点F
∴∠CDF=1/2∠ADC,∠ABE=1/2∠ABC
∴∠CDF=∠ABE
∴∠AFD=∠ABE
∴DF∥BE
∵DE∥BF
∴BEDF是平行四边形
∴BF=DE
拓展提高题
1.易错题:未给出图形,需要进行分类讨论
在平行四边形ABCD中,AD=BD,BE是AD边上的高,∠EBD=20°,则∠A= .
55°或35°
A
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
