19.3.2 矩形的判定课件(共19张PPT)
文档属性
| 名称 | 19.3.2 矩形的判定课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-15 21:59:14 | ||
图片预览




文档简介
(共19张PPT)
19.3.2
矩形的判定
沪科版
八年级下
新知导入
问题1.什么叫矩形?
答:有一个角是直角的平行四边形叫做矩形。
问题2.矩形具有哪些性质?
答:性质1.矩形的四个角都是直角.
性质2.矩形的对角线相等.
性质3.对称性:矩形是轴对称图形
思考:工人师傅在做门窗框架时,不仅要测量矩形两组对边的长度是否分别相等,还要测量它们的对角线是否相等,你能说出其中的道理吗?
新知讲解
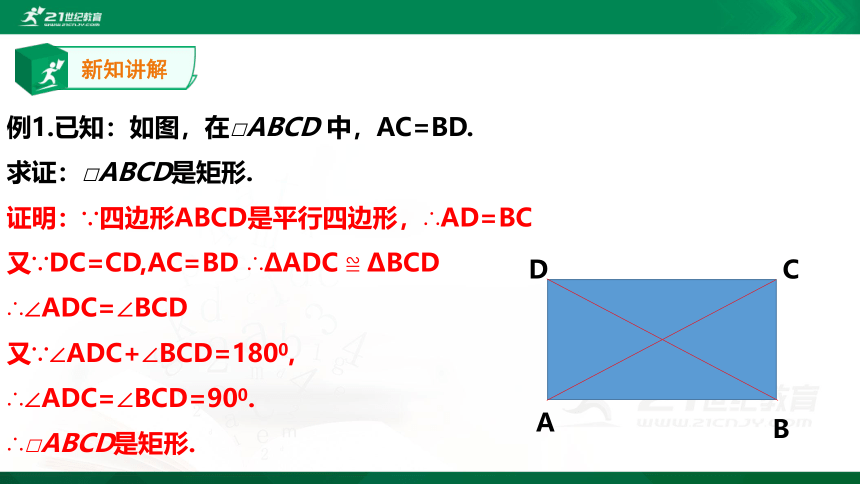
例1.已知:如图,在□ABCD
中,AC=BD.
求证:□ABCD是矩形.
证明:∵四边形ABCD是平行四边形,∴AD=BC
又∵DC=CD,AC=BD
∴?ADC
≌
?BCD
∴∠ADC=∠BCD
又∵∠ADC+∠BCD=1800,
∴∠ADC=∠BCD=900.
∴□ABCD是矩形.
新知讲解
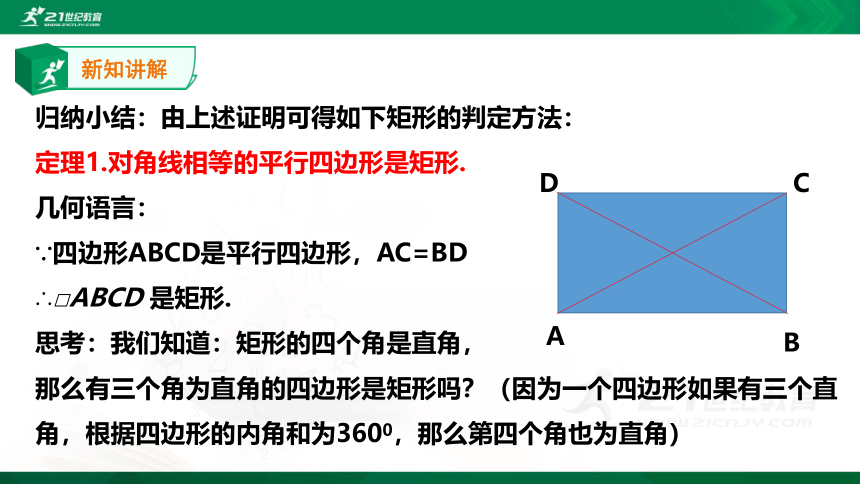
归纳小结:由上述证明可得如下矩形的判定方法:
定理1.对角线相等的平行四边形是矩形.
几何语言:
∵四边形ABCD是平行四边形,AC=BD
∴□ABCD
是矩形.
思考:我们知道:矩形的四个角是直角,
那么有三个角为直角的四边形是矩形吗?(因为一个四边形如果有三个直角,根据四边形的内角和为3600,那么第四个角也为直角)
新知讲解
例2.已知:如图,在四边形ABCD中,∠A=∠B=∠C=900.
求证:四边形ABCD是矩形.
证明:∵∠A=∠B=∠C=900.
∴∠B+∠C=1800,∠A+∠B=1800
∴AB‖CD,AD‖BC.
∴四边形ABCD是平行四边形
∴四边形ABCD是矩形.
新知讲解
归纳小结:由上述证明可得矩形的判定方法:
定理2.有三个角是直角的四边形是矩形。
几何语言:
∵∠A=∠B=∠C=900.
∴四边形ABCD
是矩形.
矩
形
判
定
如
何
应
用
呢?
新知讲解
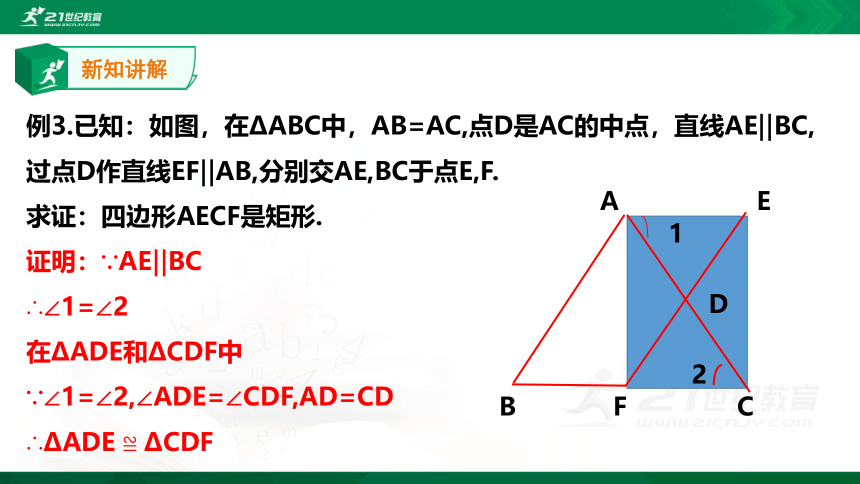
例3.已知:如图,在?ABC中,AB=AC,点D是AC的中点,直线AE‖BC,
过点D作直线EF‖AB,分别交AE,BC于点E,F.
求证:四边形AECF是矩形.
证明:∵AE‖BC
∴∠1=∠2
在?ADE和?CDF中
∵∠1=∠2,∠ADE=∠CDF,AD=CD
∴?ADE
≌
?CDF
D
新知讲解
∴AE=CF
∴四边形AECF是平行四边形
又∵四边形ABFE是平行四边形
∴EF=AB
∵AC=AB
∴EF=AC
∴四边形AECF是矩形.
D
课堂练习
1.如图,在?ABCD
中,AC
和BD
相交于点O,则下面条件能判定?ABCD
是矩形的是
( )
A.AC=BD
B.AC=BC
C.AD=BC
D.AB=AD
A
课堂练习
2.如图
□ABCD
中,
∠1=
∠2中.此时四边形ABCD
是矩形吗?为什么?
解:四边形ABCD
是矩形.
理由如下:
∵四边形ABCD
是平行四边形
∴
AO=CO,DO=BO.
又∵
∠1=
∠2,
∴AO=BO,
∴AC=BD,
∴四边形ABCD
是矩形.
1
2
课堂练习
3.在判断“一个四边形门框是否为矩形”的数学活动课上,一个合作学习小组的4位同学分别拟定了如下的方案,其中正确的是
( )
A.测量对角线是否相等
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量其中三个角是否都为直角
D
课堂练习
4.如图,直线EF∥MN,PQ
交EF、MN
于A、C
两点,AB、CB、CD、AD分别是∠EAC、
∠MCA、
∠
ACN、∠CAF
的平分线,则四边形ABCD
是
(
)
A.梯形
B.平行四边形
C.矩形
D.不能确定
C
拓展提高
5.如图,在四边形ABCD
中,AB∥CD,∠BAD=90°,AB=5,BC=12,AC=13.求证:四边形ABCD
是矩形.
证明:四边形ABCD
中,AB∥CD,∠BAD=90°,
∴∠ADC=90°.
又∵△ABC
中,AB=5,BC=12,AC=13,
满足132=52+122,即
∴△ABC
是直角三角形,且∠B=90°,
∴四边形ABCD
是矩形.
中考链接
6.(中考·南通)下列命题中正确的是(
)
A.对角线相等的四边形是矩形
B.对角线相等且有一个角是直角四边形是矩形
C.有一个角是直角四边形是矩形
D.各内角都相等的四边形是矩形
D
课堂总结
本节课你有什么收获?
矩形的判定方法除了可以根据定义判定外,还有如下两种方法:
定理1.对角线相等的平行四边形是矩形.
定理2.有三个角是直角的四边形是矩形。
板书设计
19.3.2
矩形的判定
1.定理1......................
2.定理2......................
作业布置
课
本
P97
习
题
19.3
第
3(1)题
和
第
4
题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
19.3.2
矩形的判定
沪科版
八年级下
新知导入
问题1.什么叫矩形?
答:有一个角是直角的平行四边形叫做矩形。
问题2.矩形具有哪些性质?
答:性质1.矩形的四个角都是直角.
性质2.矩形的对角线相等.
性质3.对称性:矩形是轴对称图形
思考:工人师傅在做门窗框架时,不仅要测量矩形两组对边的长度是否分别相等,还要测量它们的对角线是否相等,你能说出其中的道理吗?
新知讲解
例1.已知:如图,在□ABCD
中,AC=BD.
求证:□ABCD是矩形.
证明:∵四边形ABCD是平行四边形,∴AD=BC
又∵DC=CD,AC=BD
∴?ADC
≌
?BCD
∴∠ADC=∠BCD
又∵∠ADC+∠BCD=1800,
∴∠ADC=∠BCD=900.
∴□ABCD是矩形.
新知讲解
归纳小结:由上述证明可得如下矩形的判定方法:
定理1.对角线相等的平行四边形是矩形.
几何语言:
∵四边形ABCD是平行四边形,AC=BD
∴□ABCD
是矩形.
思考:我们知道:矩形的四个角是直角,
那么有三个角为直角的四边形是矩形吗?(因为一个四边形如果有三个直角,根据四边形的内角和为3600,那么第四个角也为直角)
新知讲解
例2.已知:如图,在四边形ABCD中,∠A=∠B=∠C=900.
求证:四边形ABCD是矩形.
证明:∵∠A=∠B=∠C=900.
∴∠B+∠C=1800,∠A+∠B=1800
∴AB‖CD,AD‖BC.
∴四边形ABCD是平行四边形
∴四边形ABCD是矩形.
新知讲解
归纳小结:由上述证明可得矩形的判定方法:
定理2.有三个角是直角的四边形是矩形。
几何语言:
∵∠A=∠B=∠C=900.
∴四边形ABCD
是矩形.
矩
形
判
定
如
何
应
用
呢?
新知讲解
例3.已知:如图,在?ABC中,AB=AC,点D是AC的中点,直线AE‖BC,
过点D作直线EF‖AB,分别交AE,BC于点E,F.
求证:四边形AECF是矩形.
证明:∵AE‖BC
∴∠1=∠2
在?ADE和?CDF中
∵∠1=∠2,∠ADE=∠CDF,AD=CD
∴?ADE
≌
?CDF
D
新知讲解
∴AE=CF
∴四边形AECF是平行四边形
又∵四边形ABFE是平行四边形
∴EF=AB
∵AC=AB
∴EF=AC
∴四边形AECF是矩形.
D
课堂练习
1.如图,在?ABCD
中,AC
和BD
相交于点O,则下面条件能判定?ABCD
是矩形的是
( )
A.AC=BD
B.AC=BC
C.AD=BC
D.AB=AD
A
课堂练习
2.如图
□ABCD
中,
∠1=
∠2中.此时四边形ABCD
是矩形吗?为什么?
解:四边形ABCD
是矩形.
理由如下:
∵四边形ABCD
是平行四边形
∴
AO=CO,DO=BO.
又∵
∠1=
∠2,
∴AO=BO,
∴AC=BD,
∴四边形ABCD
是矩形.
1
2
课堂练习
3.在判断“一个四边形门框是否为矩形”的数学活动课上,一个合作学习小组的4位同学分别拟定了如下的方案,其中正确的是
( )
A.测量对角线是否相等
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量其中三个角是否都为直角
D
课堂练习
4.如图,直线EF∥MN,PQ
交EF、MN
于A、C
两点,AB、CB、CD、AD分别是∠EAC、
∠MCA、
∠
ACN、∠CAF
的平分线,则四边形ABCD
是
(
)
A.梯形
B.平行四边形
C.矩形
D.不能确定
C
拓展提高
5.如图,在四边形ABCD
中,AB∥CD,∠BAD=90°,AB=5,BC=12,AC=13.求证:四边形ABCD
是矩形.
证明:四边形ABCD
中,AB∥CD,∠BAD=90°,
∴∠ADC=90°.
又∵△ABC
中,AB=5,BC=12,AC=13,
满足132=52+122,即
∴△ABC
是直角三角形,且∠B=90°,
∴四边形ABCD
是矩形.
中考链接
6.(中考·南通)下列命题中正确的是(
)
A.对角线相等的四边形是矩形
B.对角线相等且有一个角是直角四边形是矩形
C.有一个角是直角四边形是矩形
D.各内角都相等的四边形是矩形
D
课堂总结
本节课你有什么收获?
矩形的判定方法除了可以根据定义判定外,还有如下两种方法:
定理1.对角线相等的平行四边形是矩形.
定理2.有三个角是直角的四边形是矩形。
板书设计
19.3.2
矩形的判定
1.定理1......................
2.定理2......................
作业布置
课
本
P97
习
题
19.3
第
3(1)题
和
第
4
题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
