六年级北师大版数学下册第一单元复习课件(35张ppt)
文档属性
| 名称 | 六年级北师大版数学下册第一单元复习课件(35张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-16 00:00:00 | ||
图片预览







文档简介
(共35张PPT)
复习第一单元
圆柱与圆锥
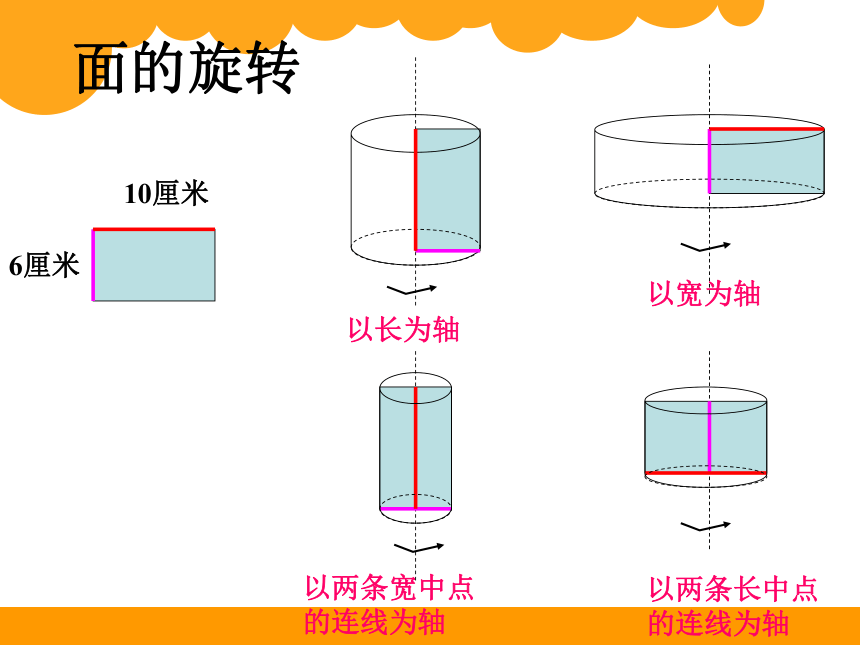
以长为轴
以宽为轴
10厘米
6厘米
以两条宽中点的连线为轴
以两条长中点的连线为轴
面的旋转
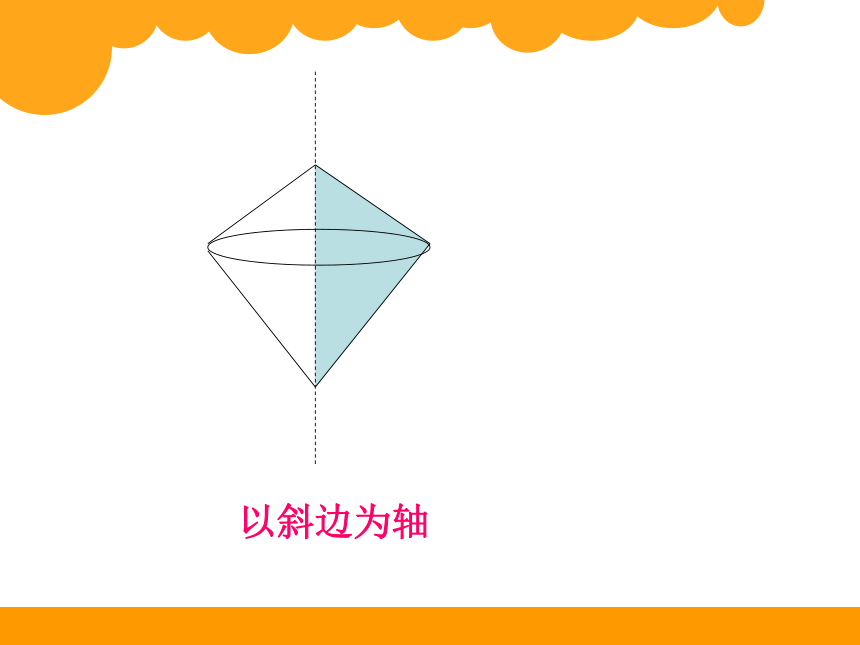
以斜边为轴
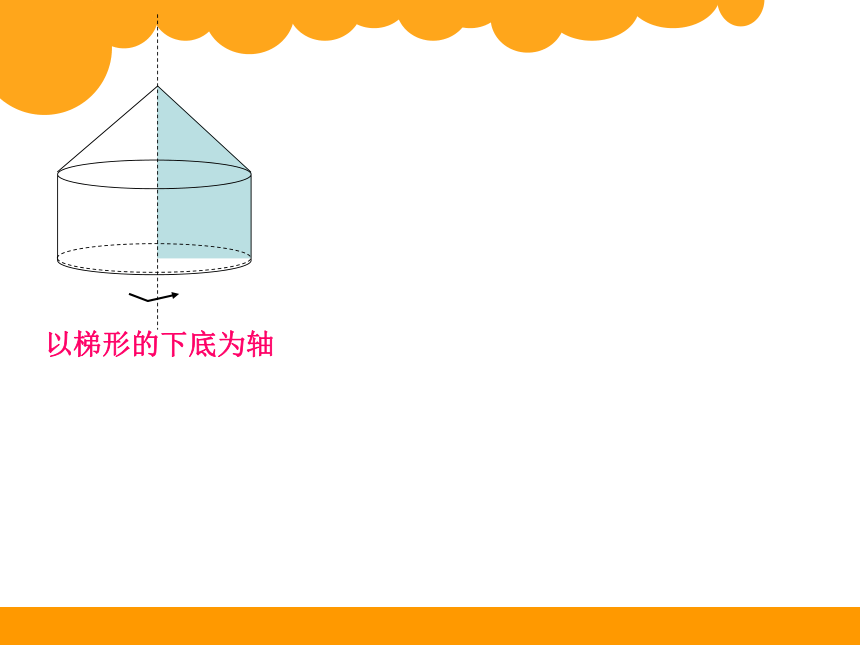
以梯形的下底为轴
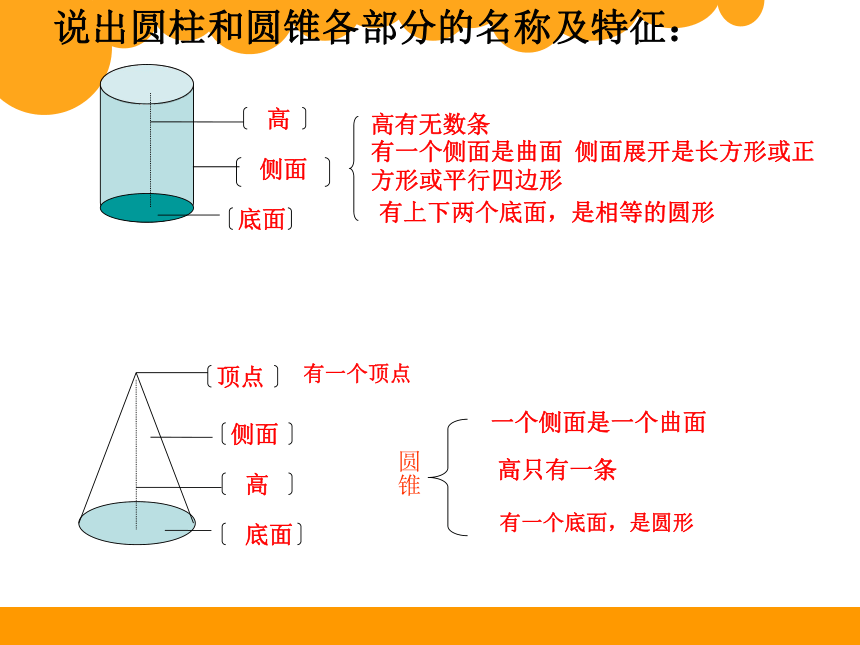
说出圆柱和圆锥各部分的名称及特征:
高
有上下两个底面,是相等的圆形
侧面
有一个侧面是曲面
侧面展开是长方形或正
方形或平行四边形
底面
高有无数条
顶点
侧面
一个侧面是一个曲面
高
高只有一条
底面
圆锥
有一个顶点
有一个底面,是圆形
归纳总结
补充:
把圆柱平行于底面进行切割,切面是和底面大小
相同的两个圆;
把圆柱沿底面直径垂直于底面进行切割,切面是
两个完全相同的长方形。
补充:
把圆锥平行于底面切割,切面是两个完全相同的圆,该圆要比圆锥的底面圆小;
把圆锥垂直于底面进行切割,
切面则是两个完全相同的等腰三角形。
归纳总结
圆锥的特征:圆锥的底面是一个圆;
圆锥的侧面是一个曲面;
圆锥只有一条高。
补充:
把圆锥平行于底面切割,切面是两个完全相同的圆,
该圆要比圆锥的底面圆小;
把圆锥垂直于底面进行切割,
切面则是两个完全相同的等腰三角形。
填空题
1.圆柱的上下两个底面都是(),他们的面积()。
2.圆柱的高有()条,圆锥的高有()条。
3.从圆锥的()到()的距离是圆锥的高。
4.以长方形的一边为轴,旋转一周能得到一个()。
圆柱的表面积
圆柱的侧面积=底面周长x高,用字母公式表示S侧=Ch
圆柱的表面积=侧面积+2x底面积,用字母公式表示为S表=2S底+S侧
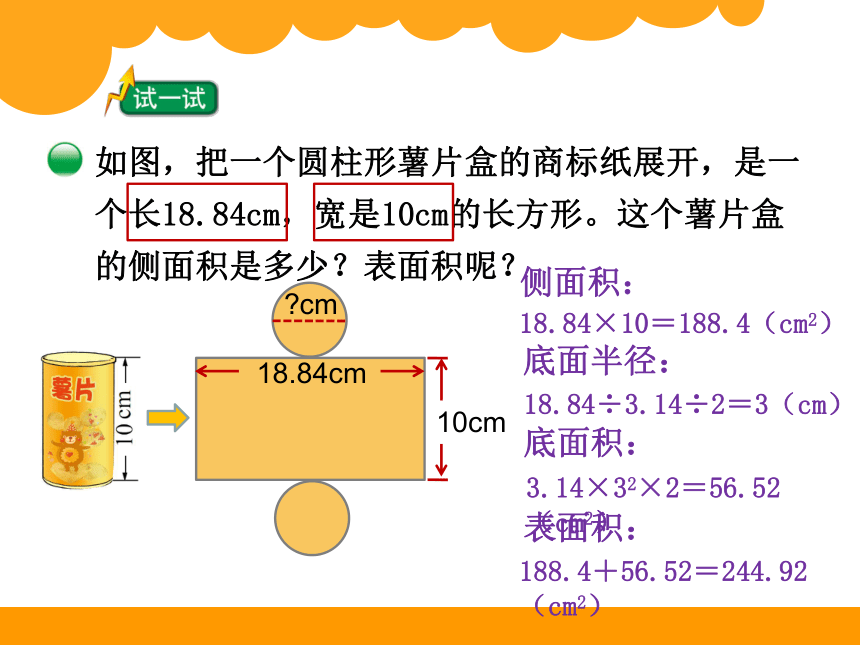
如图,把一个圆柱形薯片盒的商标纸展开,是一个长18.84cm,宽是10cm的长方形。这个薯片盒的侧面积是多少?表面积呢?
10cm
18.84cm
?cm
侧面积:
18.84×10=188.4(cm2)
底面半径:
18.84÷3.14÷2=3(cm)
底面积:
3.14×32×2=56.52(cm2)
表面积:
188.4+56.52=244.92(cm2)
解决问题
1.做一个底面直径为20厘米,长为60厘米的通风管。至少需要铁皮多少平方厘米?
2.?把一个底面半径6分米,高1米的圆柱切成3个小圆柱,表面积增加了多少?
3.工人叔叔把一根高1米的圆柱形木料,沿与底面平行的方向锯成两段,这时表面积比原来增加了25.12平方分米,求这根料的底面半径是多少?
4.一圆柱底面直径是4米,高是6米,沿着底面直径把圆柱切成两半,求这个圆柱的表面积增加多少?
圆柱的体积
圆柱的体积=底面积X高,
用字母公式表示为v=S底h=πr?h
圆锥的体积
圆锥的体积等于和它等底等高的圆柱的体积的三分之一,用字母公式表示为
面的旋转
1.点动成线,线动成面,面动成体。
2.圆柱的特征:圆柱有三个面,底面是两个大小相同的圆;侧面是一个曲面,展开后得到一个长方形,长是圆柱底面的周长,宽是圆柱的高;两个底面之间的距离是圆柱的高,圆柱有无数条高
3.圆锥的特征:圆锥有两个面,底面是个圆,侧面是一个曲面,展开后是一个扇形;从圆锥的顶点到底面圆心的距离是圆锥的高,圆锥只有一条高。
填空题
1.把一段圆柱形钢材切削成一个最大的圆锥,切削掉的部分的质量为8千克,这段圆柱形钢材质量为()千克。
2.一个高为12厘米的圆锥形量杯里装满了水,如果将这些水倒入与它底面积相等的圆柱形量杯中,水面高()厘米。
3.圆柱的体积比和它等底等高的体积大()倍。圆锥体积比和它等底等高的圆柱体积少()。
巩固练习
1.一个底面半径是4厘米,高是9厘米的圆柱体木材,削成一个最大的圆锥,这个圆锥的体积是多少立方厘米?削去部分的体积是多少??
2.一个圆锥形沙堆,底面周长是12.56米,高6米,将这些沙铺在宽10米的道路上铺4厘米厚,可以铺多少米长?
3.一个圆柱体和一个圆锥体等底等高,它们的体积相差50.24立方厘米如果圆锥体的底面半径是2厘米,这个圆锥体的高是多少厘米?
4.把一个体积是282.6立方厘米的铁块熔铸成一个底面半径是6厘米的圆锥形机器零件,求圆锥零件的高?
5.把一个底半径为5厘米的圆柱铁块放入一个底半径10厘米,高14厘米的容器里,水面上升了3厘米,求这个圆柱铁块的高?
比例的意义和基本性质
1.比例的意义;表示两个比相等的式子叫比例。组成比例的四个数叫比例的项,两端的两项叫比例的外项,中间的两项叫比例的内向。
2.比例的基本性质;在比例里两个内项积等于两个外项积。
3.解比例;解比例的基本依据是比例的基本性,已知比例的任意三项,都可以求出另外一项。
比例的应用
1.比例尺的意义;一幅图的图上距离和实际距离的比,叫这幅图的比例尺。
2.用比例尺解决实际问题;一般根据“
=比例尺“来解
3.图形的放大和缩小;n:1的比放大,就是把图形的每条边都放大到原来的n倍;将图形按1:n缩小,就是把图形的每条边都缩小到原来
的
4.用比例解决问题;(1)分析题意,找出题目中的两种变量。
(2)分析这两种变量成什么什么比例关系。
(3)根据这样的比例列出等式。
(
4
)解比例,求结果。
1.40千克小麦能磨面粉32千克,照这样计算,7吨小麦能磨面粉多少千克?
测量小组把一米长的竹竿直立在地面上,测得它的影子长度是1.6米,同时测得电线杆的影子长度是4米,求电线杆高多少米?
修路队修一段路,头3天修了135米,照这样速度,又修了8天才修完这段路,这段路长多少米?
一个房间,用边长3分米的方砖铺地,需要432块,如果改用边长4分米的方砖铺地,需要多少块?
100千克黄豆可以榨油13千克,照这样计算,要榨豆油6.5吨,需黄豆多少吨?
农场用3辆拖拉机耕地,每天共耕225公顷,如果用5辆同样的拖拉机,每天共耕在多少公顷?
用5辆同样汽车运粮食一次能运22.5吨,照这样计算,要把36吨粮食一次运完,需要增加多少辆这样的汽车?
某印刷厂计划三月份印刷课本20000本,结果上旬就印刷7000本,照这样速度,三月份可以多印刷多少本?
广州到福州的实际距离是720千米,在一幅地图上量得两地的图上距离是12厘米。求这幅地图的比例尺。
在比例尺是1:6000000的中国地图上,量得广州到深圳的距离是1.8厘米。请你计算,广州到深圳的实际距离大约是多少千米?
一个机器零件长3厘米,画在一张比例尺为20:1的图纸上,应画多长?
在一张比例尺是1:1000的设计图上,有一个长方形建筑物,量得建筑物的长是6厘米,宽是4厘米,这个建筑物的实际面积是多少平方米?
豫州到淮安的距离大约是230千米,在比例尺是1:2300000的地图上,两地的距离是多少厘米?
说出圆柱和圆锥各部分的名称及特征:
高
有无数条
侧面
展开后是长方形或正方形
底面
有两个底面,是相等的圆形
顶点
有一个顶点
侧面
展开后是扇形
高
只有一条
有一个底面,是圆形
圆柱的体积公式用字母表示是(
)。如果已知d=6厘米,h=10厘米。那么圆柱的体积是(
)立方厘米。如果已知c=6.28分米,h=5分米。那么圆柱的体积是(
)立方分米。
V=s
h
282.6
15.7
底面
绿色圃中小学教育网http://www.lspjy.com
?一、填空题:
?3等于乙数的75%,那么甲数与乙数的比是??()?:?()?。?
2.学校操场的长是100米,宽是80米,如果画在比例尺是1:1000的图纸上,长应画(????),宽应画(?????)。?
3.一种微型零件的长15毫米,画在图纸上长20厘米,这幅图的比例尺是??????????????4.一个精密零件长5毫米,把它画在比例尺是10:1的图纸上,长是(??????)。
5.如果A的
和B的
相等,那么??A:B=(??):(??)
如图,要做一个圆柱形纸盒。如果接口不计,至少需要用多大面积的纸板?
10cm
30cm
底面周长
高
圆柱的侧面积=底面周长×高
你能计算出“至少需要多大面积的纸板”吗?
10cm
30cm
侧面积:
底面积:
表面积:
答:至少需要2512平方厘米的纸板。
2×3.14×10×30=1884(cm2)
3.14×102×2=628(cm2)
1884+628=2512(cm2)
一个圆柱的高是15厘米,底面半径是5厘米,它的表面积是多少?
2×3.14×5×15
3.14
×52
答:它的表面积是628平方厘米。
15
5
5
15
5
2
×3.14
×5
471+78.5
×2
2
侧面积:
底面积:
表面积:
=471(平方厘米)
=78.5(平方厘米)
=628(平方厘米)
1.连一连,并在括号中填出相应的数。
(
)
(
)
(
)
(
)
21.98cm
4cm
9.42cm
8cm
10
5
5
10
2.求圆柱的表面积。
如图,做一个无盖的圆柱形铁皮水桶,底面直径为4dm,高为5dm,至少需要用多大面积的铁皮?
侧面积+一个底面积
侧面积:
底面积:
表面积:
3.14×4×5=62.8(dm2)
3.14×(4÷2)2=12.56(dm2)
62.8+12.56=75.36(dm2)
4dm
5dm
答:至少需要75.36平方分米的铁皮。
3
一个没有盖的圆柱形铁皮水桶,高是24厘米,底面直径是20厘米,做这个水桶要用铁皮多少平方厘米?(得数保留整百平方厘米?)
3.14×20×24
3.14
×(20÷2)2
1507.2+314
答:做这个水桶需用铁皮约1900平方厘米。
(1)水桶的侧面积:
(2)水桶的底面积:
(3)需要的铁皮:
=1507.2(平方厘米)
=314(平方厘米)
=1821.2
≈1900(平方厘米)
3.压路机前轮直径是1.6m,长2m,它转动一周,压
路的面积是多少平方米?
4.制作一个底面直径20cm,长50cm的圆柱形通风管,至少要用多少平方厘米的铁皮?
5.一个圆柱形水池,水池内壁和底部都镶上磁砖,
水池内部底面周长25.12m,池深1.2m,镶磁砖的
面积是多少平方米?
求圆柱侧面积
求圆柱侧面积
求圆柱侧面积和一个底面积
3.14×1.6×2=10.048(m2)
3.14×20×50=3140(cm2)
底面积:3.14×(25.12÷3.14÷2)2=50.24(m2)
侧面积:25.12×1.2=30.144(m2)
表面积:30.144+50.24=80.384(m2)
6.油桶的表面要刷上防锈油漆,每平方
米需用防锈油漆0.2kg,漆一个油桶
大约需要多少防锈油漆?(结果保留
两位小数)
求圆柱侧面积和两个底面积
侧面积:3.14×0.6×1=1.884(m2)
底面积:3.14×(0.6÷2)2×2=0.5652(m2)
表面积:1.884+0.5652=2.4492(m2)
油漆:2.4492×0.2≈0.49(kg)
7.做一做。
⑴
找一个圆柱形物体,量出它的高和底面直径,
计算出它的表面积。
⑵
制作一个底面直径和高都是10cm的圆柱形纸盒。
8.如图,用下面的长方形硬纸卷成圆柱形小笔筒,再
给这个笔筒配一个底,想一想,至少需要多少平方
厘米的硬纸片?
你学到了什么?
复习第一单元
圆柱与圆锥
以长为轴
以宽为轴
10厘米
6厘米
以两条宽中点的连线为轴
以两条长中点的连线为轴
面的旋转
以斜边为轴
以梯形的下底为轴
说出圆柱和圆锥各部分的名称及特征:
高
有上下两个底面,是相等的圆形
侧面
有一个侧面是曲面
侧面展开是长方形或正
方形或平行四边形
底面
高有无数条
顶点
侧面
一个侧面是一个曲面
高
高只有一条
底面
圆锥
有一个顶点
有一个底面,是圆形
归纳总结
补充:
把圆柱平行于底面进行切割,切面是和底面大小
相同的两个圆;
把圆柱沿底面直径垂直于底面进行切割,切面是
两个完全相同的长方形。
补充:
把圆锥平行于底面切割,切面是两个完全相同的圆,该圆要比圆锥的底面圆小;
把圆锥垂直于底面进行切割,
切面则是两个完全相同的等腰三角形。
归纳总结
圆锥的特征:圆锥的底面是一个圆;
圆锥的侧面是一个曲面;
圆锥只有一条高。
补充:
把圆锥平行于底面切割,切面是两个完全相同的圆,
该圆要比圆锥的底面圆小;
把圆锥垂直于底面进行切割,
切面则是两个完全相同的等腰三角形。
填空题
1.圆柱的上下两个底面都是(),他们的面积()。
2.圆柱的高有()条,圆锥的高有()条。
3.从圆锥的()到()的距离是圆锥的高。
4.以长方形的一边为轴,旋转一周能得到一个()。
圆柱的表面积
圆柱的侧面积=底面周长x高,用字母公式表示S侧=Ch
圆柱的表面积=侧面积+2x底面积,用字母公式表示为S表=2S底+S侧
如图,把一个圆柱形薯片盒的商标纸展开,是一个长18.84cm,宽是10cm的长方形。这个薯片盒的侧面积是多少?表面积呢?
10cm
18.84cm
?cm
侧面积:
18.84×10=188.4(cm2)
底面半径:
18.84÷3.14÷2=3(cm)
底面积:
3.14×32×2=56.52(cm2)
表面积:
188.4+56.52=244.92(cm2)
解决问题
1.做一个底面直径为20厘米,长为60厘米的通风管。至少需要铁皮多少平方厘米?
2.?把一个底面半径6分米,高1米的圆柱切成3个小圆柱,表面积增加了多少?
3.工人叔叔把一根高1米的圆柱形木料,沿与底面平行的方向锯成两段,这时表面积比原来增加了25.12平方分米,求这根料的底面半径是多少?
4.一圆柱底面直径是4米,高是6米,沿着底面直径把圆柱切成两半,求这个圆柱的表面积增加多少?
圆柱的体积
圆柱的体积=底面积X高,
用字母公式表示为v=S底h=πr?h
圆锥的体积
圆锥的体积等于和它等底等高的圆柱的体积的三分之一,用字母公式表示为
面的旋转
1.点动成线,线动成面,面动成体。
2.圆柱的特征:圆柱有三个面,底面是两个大小相同的圆;侧面是一个曲面,展开后得到一个长方形,长是圆柱底面的周长,宽是圆柱的高;两个底面之间的距离是圆柱的高,圆柱有无数条高
3.圆锥的特征:圆锥有两个面,底面是个圆,侧面是一个曲面,展开后是一个扇形;从圆锥的顶点到底面圆心的距离是圆锥的高,圆锥只有一条高。
填空题
1.把一段圆柱形钢材切削成一个最大的圆锥,切削掉的部分的质量为8千克,这段圆柱形钢材质量为()千克。
2.一个高为12厘米的圆锥形量杯里装满了水,如果将这些水倒入与它底面积相等的圆柱形量杯中,水面高()厘米。
3.圆柱的体积比和它等底等高的体积大()倍。圆锥体积比和它等底等高的圆柱体积少()。
巩固练习
1.一个底面半径是4厘米,高是9厘米的圆柱体木材,削成一个最大的圆锥,这个圆锥的体积是多少立方厘米?削去部分的体积是多少??
2.一个圆锥形沙堆,底面周长是12.56米,高6米,将这些沙铺在宽10米的道路上铺4厘米厚,可以铺多少米长?
3.一个圆柱体和一个圆锥体等底等高,它们的体积相差50.24立方厘米如果圆锥体的底面半径是2厘米,这个圆锥体的高是多少厘米?
4.把一个体积是282.6立方厘米的铁块熔铸成一个底面半径是6厘米的圆锥形机器零件,求圆锥零件的高?
5.把一个底半径为5厘米的圆柱铁块放入一个底半径10厘米,高14厘米的容器里,水面上升了3厘米,求这个圆柱铁块的高?
比例的意义和基本性质
1.比例的意义;表示两个比相等的式子叫比例。组成比例的四个数叫比例的项,两端的两项叫比例的外项,中间的两项叫比例的内向。
2.比例的基本性质;在比例里两个内项积等于两个外项积。
3.解比例;解比例的基本依据是比例的基本性,已知比例的任意三项,都可以求出另外一项。
比例的应用
1.比例尺的意义;一幅图的图上距离和实际距离的比,叫这幅图的比例尺。
2.用比例尺解决实际问题;一般根据“
=比例尺“来解
3.图形的放大和缩小;n:1的比放大,就是把图形的每条边都放大到原来的n倍;将图形按1:n缩小,就是把图形的每条边都缩小到原来
的
4.用比例解决问题;(1)分析题意,找出题目中的两种变量。
(2)分析这两种变量成什么什么比例关系。
(3)根据这样的比例列出等式。
(
4
)解比例,求结果。
1.40千克小麦能磨面粉32千克,照这样计算,7吨小麦能磨面粉多少千克?
测量小组把一米长的竹竿直立在地面上,测得它的影子长度是1.6米,同时测得电线杆的影子长度是4米,求电线杆高多少米?
修路队修一段路,头3天修了135米,照这样速度,又修了8天才修完这段路,这段路长多少米?
一个房间,用边长3分米的方砖铺地,需要432块,如果改用边长4分米的方砖铺地,需要多少块?
100千克黄豆可以榨油13千克,照这样计算,要榨豆油6.5吨,需黄豆多少吨?
农场用3辆拖拉机耕地,每天共耕225公顷,如果用5辆同样的拖拉机,每天共耕在多少公顷?
用5辆同样汽车运粮食一次能运22.5吨,照这样计算,要把36吨粮食一次运完,需要增加多少辆这样的汽车?
某印刷厂计划三月份印刷课本20000本,结果上旬就印刷7000本,照这样速度,三月份可以多印刷多少本?
广州到福州的实际距离是720千米,在一幅地图上量得两地的图上距离是12厘米。求这幅地图的比例尺。
在比例尺是1:6000000的中国地图上,量得广州到深圳的距离是1.8厘米。请你计算,广州到深圳的实际距离大约是多少千米?
一个机器零件长3厘米,画在一张比例尺为20:1的图纸上,应画多长?
在一张比例尺是1:1000的设计图上,有一个长方形建筑物,量得建筑物的长是6厘米,宽是4厘米,这个建筑物的实际面积是多少平方米?
豫州到淮安的距离大约是230千米,在比例尺是1:2300000的地图上,两地的距离是多少厘米?
说出圆柱和圆锥各部分的名称及特征:
高
有无数条
侧面
展开后是长方形或正方形
底面
有两个底面,是相等的圆形
顶点
有一个顶点
侧面
展开后是扇形
高
只有一条
有一个底面,是圆形
圆柱的体积公式用字母表示是(
)。如果已知d=6厘米,h=10厘米。那么圆柱的体积是(
)立方厘米。如果已知c=6.28分米,h=5分米。那么圆柱的体积是(
)立方分米。
V=s
h
282.6
15.7
底面
绿色圃中小学教育网http://www.lspjy.com
?一、填空题:
?3等于乙数的75%,那么甲数与乙数的比是??()?:?()?。?
2.学校操场的长是100米,宽是80米,如果画在比例尺是1:1000的图纸上,长应画(????),宽应画(?????)。?
3.一种微型零件的长15毫米,画在图纸上长20厘米,这幅图的比例尺是??????????????4.一个精密零件长5毫米,把它画在比例尺是10:1的图纸上,长是(??????)。
5.如果A的
和B的
相等,那么??A:B=(??):(??)
如图,要做一个圆柱形纸盒。如果接口不计,至少需要用多大面积的纸板?
10cm
30cm
底面周长
高
圆柱的侧面积=底面周长×高
你能计算出“至少需要多大面积的纸板”吗?
10cm
30cm
侧面积:
底面积:
表面积:
答:至少需要2512平方厘米的纸板。
2×3.14×10×30=1884(cm2)
3.14×102×2=628(cm2)
1884+628=2512(cm2)
一个圆柱的高是15厘米,底面半径是5厘米,它的表面积是多少?
2×3.14×5×15
3.14
×52
答:它的表面积是628平方厘米。
15
5
5
15
5
2
×3.14
×5
471+78.5
×2
2
侧面积:
底面积:
表面积:
=471(平方厘米)
=78.5(平方厘米)
=628(平方厘米)
1.连一连,并在括号中填出相应的数。
(
)
(
)
(
)
(
)
21.98cm
4cm
9.42cm
8cm
10
5
5
10
2.求圆柱的表面积。
如图,做一个无盖的圆柱形铁皮水桶,底面直径为4dm,高为5dm,至少需要用多大面积的铁皮?
侧面积+一个底面积
侧面积:
底面积:
表面积:
3.14×4×5=62.8(dm2)
3.14×(4÷2)2=12.56(dm2)
62.8+12.56=75.36(dm2)
4dm
5dm
答:至少需要75.36平方分米的铁皮。
3
一个没有盖的圆柱形铁皮水桶,高是24厘米,底面直径是20厘米,做这个水桶要用铁皮多少平方厘米?(得数保留整百平方厘米?)
3.14×20×24
3.14
×(20÷2)2
1507.2+314
答:做这个水桶需用铁皮约1900平方厘米。
(1)水桶的侧面积:
(2)水桶的底面积:
(3)需要的铁皮:
=1507.2(平方厘米)
=314(平方厘米)
=1821.2
≈1900(平方厘米)
3.压路机前轮直径是1.6m,长2m,它转动一周,压
路的面积是多少平方米?
4.制作一个底面直径20cm,长50cm的圆柱形通风管,至少要用多少平方厘米的铁皮?
5.一个圆柱形水池,水池内壁和底部都镶上磁砖,
水池内部底面周长25.12m,池深1.2m,镶磁砖的
面积是多少平方米?
求圆柱侧面积
求圆柱侧面积
求圆柱侧面积和一个底面积
3.14×1.6×2=10.048(m2)
3.14×20×50=3140(cm2)
底面积:3.14×(25.12÷3.14÷2)2=50.24(m2)
侧面积:25.12×1.2=30.144(m2)
表面积:30.144+50.24=80.384(m2)
6.油桶的表面要刷上防锈油漆,每平方
米需用防锈油漆0.2kg,漆一个油桶
大约需要多少防锈油漆?(结果保留
两位小数)
求圆柱侧面积和两个底面积
侧面积:3.14×0.6×1=1.884(m2)
底面积:3.14×(0.6÷2)2×2=0.5652(m2)
表面积:1.884+0.5652=2.4492(m2)
油漆:2.4492×0.2≈0.49(kg)
7.做一做。
⑴
找一个圆柱形物体,量出它的高和底面直径,
计算出它的表面积。
⑵
制作一个底面直径和高都是10cm的圆柱形纸盒。
8.如图,用下面的长方形硬纸卷成圆柱形小笔筒,再
给这个笔筒配一个底,想一想,至少需要多少平方
厘米的硬纸片?
你学到了什么?
