24.2.1 点与圆、直线与圆的位置关系 课件(共22张PPT)
文档属性
| 名称 | 24.2.1 点与圆、直线与圆的位置关系 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-16 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
人教版
九上
第二十四章
圆
第一节
点与圆的位置关系
第一节
点与圆的位置关系
1.上节课我们学习了圆的概念,请同学们回答一下什么是圆?
(在平面内一条线段OA绕着它一个固定的端点O旋转一周,另外一个端点A所形成的图形。)【也可以这样说过定点O等于定长OA的所有点的集合】
我们来看这样一个题目
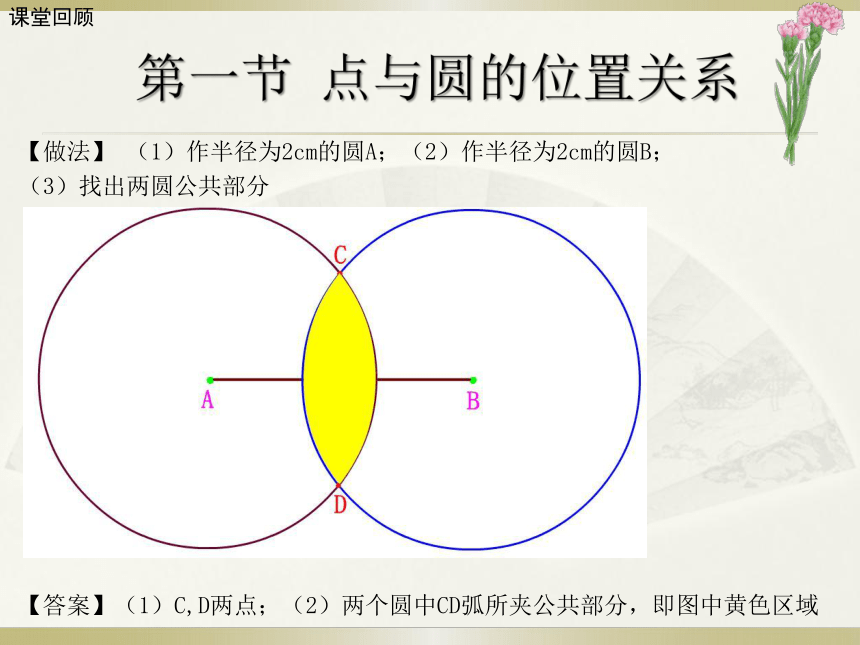
【兔爸数学】设AB=3cm,作图说明满足下列要求的图形:
(1)到点A和点B的距离都等于2cm的所有点组成的图形;
(2)到点A和点B的距离都小于2cm的所有点组成的图形。
课堂回顾
第一节
点与圆的位置关系
课堂回顾
【做法】
(1)作半径为2cm的圆A;(2)作半径为2cm的圆B;
(3)找出两圆公共部分
【答案】(1)C,D两点;(2)两个圆中CD弧所夹公共部分,即图中黄色区域
第一节
点与圆的位置关系
2.了解什么是圆心,什么是半径,直径,什么是弧,什么是弦、什么是圆心角,什么是圆周角?现在我给大家一个空白纸,大家在这张纸上画出圆,半径,直径,弦,圆周角并标记出来,圆心角;看谁画的又准确又快!
第一节
点与圆的位置关系
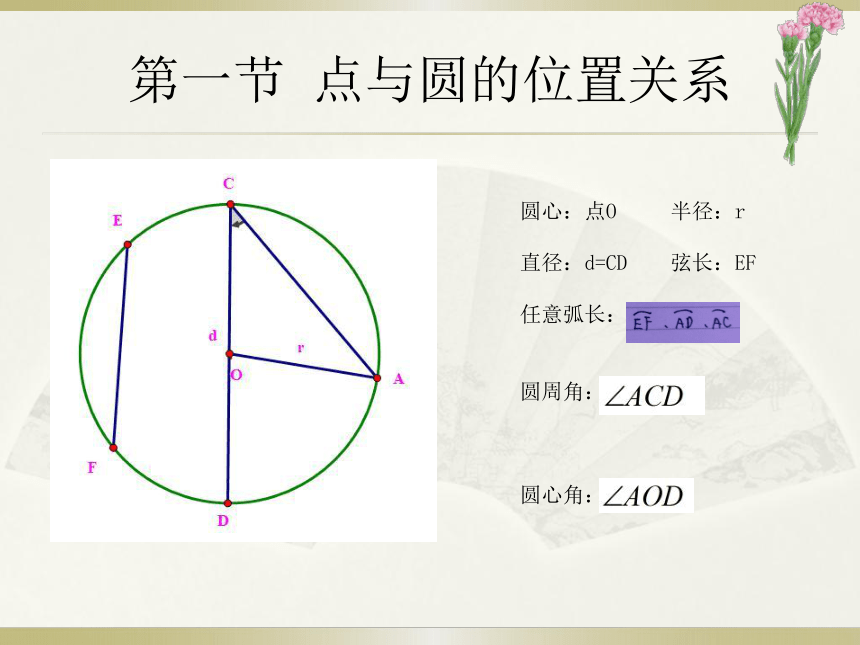
圆心:点O
半径:r
直径:d=CD
弦长:EF
任意弧长:
圆周角:
圆心角:
第一节
点与圆的位置关系
3.我们还学习了垂径定理;弦、弧、圆心角的关系以及圆周角和圆心角的关系,是什么呢?你还记得吗?
(垂直于弦的直径平分弦,并且平分弦所对的两条弧---垂径定理)
(在同圆或者等圆中,相等的圆心角所对的弧相等,所对的弦也相等;反过来也可以这样说:在同圆或者等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等;如果两条弦相等,那么他们所对的圆心角相等,所对的弧也相等----弦、弧、圆心角的关系)
(一条弧所得圆周角等于它所对的圆心角的一半,同弧或者等弧所对的圆周角相等,半圆或者直径所对的圆周角是直角,反之直角所对的弦是直径----
圆心角与圆周角的关系)
第一节
点与圆的位置关系
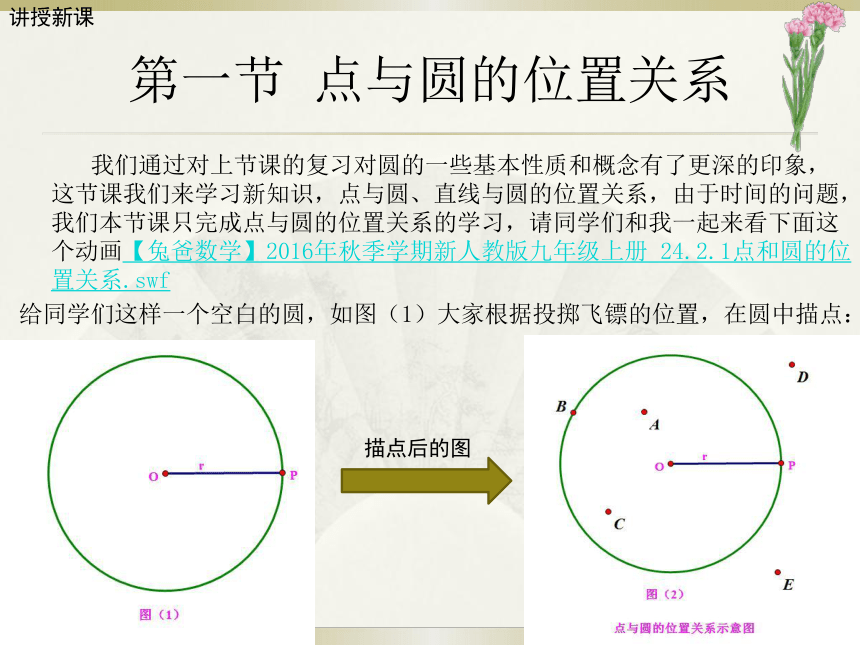
我们通过对上节课的复习对圆的一些基本性质和概念有了更深的印象,这节课我们来学习新知识,点与圆、直线与圆的位置关系,由于时间的问题,我们本节课只完成点与圆的位置关系的学习,请同学们和我一起来看下面这个动画【兔爸数学】2016年秋季学期新人教版九年级上册
24.2.1点和圆的位置关系.swf
给同学们这样一个空白的圆,如图(1)大家根据投掷飞镖的位置,在圆中描点:
讲授新课
描点后的图
第一节
点与圆的位置关系
通过作图描点大家发现了什么呢?如果用数学的语言表达出来又该怎么描述呢?
我们一起来说明,已知圆的的半径为r,我们将这些点到圆心的距离分别记为:a、b、c、d、e
通过标记和比较得出:[ar,e>r]
第一节
点与圆的位置关系
由此我们得出这样的结论:点与圆的位置关系有三种。
(1)当点在圆外时,这个点到圆心的距离____半径;
【大于】
(2)当点在圆上时,这个点到圆心的距离____半径;
【等于】
(3)当点在圆内时,这个点到圆心的距离____半径;
【小于】
通过对点和圆的位置关系的学习,我们来进一步探究这样一个问题:我们知道,已知圆心和半径,可以作一个圆,经过一个已知点A能不能作圆,这样的圆你能作出多少个?经过两个已知点A,B能不能作圆?如果能,圆心分布有什么特点?
概念总结,探究思考
第一节
点与圆的位置关系
作圆的关键是确定圆心和半径的大小,对于经过一个已知点作圆的问题,
首要任务就是确定圆心,圆心确定了,半径也就随之确定了,
那么问题就简单了,经过点A做圆,只要在点A以外任意一点确定为圆心,
圆心与点A的距离为半径作圆即可,我们可以画出图形如下图(3):
探究思考
由此可知经过一个已知点A能作圆,
这样的圆你能作出无数个
第一节
点与圆的位置关系
再来看经过两个点A,B做圆的问题,也就是说圆心到点A和点B的距离相等,那么我们根据以前所学知识知道,到线段两个端点的距离相等的点就是这样一条线即线段AB的垂直平分线,也就是说只要圆心在这条线上,都能满足到点A,B距离相等,如下图(4)所示:
探究思考
经过两个已知点A,B能作圆,
这样的圆也是有无数个的。
第一节
点与圆的位置关系
我们进一步思考:经过不在同一直线上的三点A,B,C能不能作圆?如果能,如何确定所作圆的圆心?如下图所示我们画出图形:
【思路分析】根据题目我们可以这样理解:我们要作这样一个圆能满足点A,B,C都在圆上,也就是说圆心的距离到这三个点的距离相等都等于半径,根据上面我们经过两个点的圆,就在这条线段的垂直平分线上,因此要满足经过三个点,就是说圆心都在这三条线段的垂直平分线上,于是我们连接这三个点,作出这个三角形的三条垂直平分线,作图如下:
探究思考
第一节
点与圆的位置关系
如图,我们作线段AC的垂直平分线为m,做线段BC的垂直平分线为n,做线段AB的垂直平分线为l,三条垂直平分线的交点为点O,由此可以得出OA-OB=OC,即就是说交点O即为圆心,就有OA-OB=OC=OD=r
思考总结
第一节
点与圆的位置关系
由此我们得出这样的结论:不在同一直线的三个点确定一个圆。
如上图中经过三角形ABC的三个顶点可以作一个圆,这个圆叫做三角形的外接圆;外接圆的圆心是这个三角形的三条边的垂直平分线的交点,叫做这个三角形的外心。
我们知道了不在同一直线的三个点可以确定一个圆,那么在同一直线的三个点能确定一个圆吗?(想一想)
第一节
点与圆的位置关系
思考后我们一起来解决,我们不妨假设存在这样的一个圆满足经过这三个点A,B,C,设圆心为点O,那么点O在线段AB的垂直平分线上,也在线段AC的垂直平分线上,同时也在线段BC的垂直平分线上,根据之前所学知识,做出这三个线段的垂直平分线,观察可知三条线段的垂直平分线都相互垂直,这和我们之前所学的过一个点有且只有一条直线与已知直线相互垂直相矛盾,所以这个结论是不成立的,作图如下。
第一节
点与圆的位置关系
上面证明“经过同一条直线上的三个点不能作圆”的方法与我们之前所学过的证明不同,他不是直接从命题的已知得出结论,而是假设命题的结论不成立(即假设经过同一直线上的三个点可以做一个圆),由此经过推理得出矛盾,由此矛盾断定所做假设不正确,从而得到原命题成立,这种方法叫做反证法。
在某种情形下,反证法是很有效的证明方法。例如用反证法证明平行线的性质:“两直线平行,同位角相等”在这里我们就不演示证明过程了,同学们自己思考证明,然后参照课本94页验证自己证明方法是否正确。
第一节
点与圆的位置关系
趣味数学-----反证法
反证法一节,可以说是一个难点.因为以前我们的证明,所采用的方法均为直接证法,由已知到结论,顺理成章.而对于属于间接证法的反证法,许多同学正是难以走出直接证法的局限,从而不能深刻或正确理解反证法思想.其实,反证法作为证明方法的一种,有时起着直接证法不可替代的作用.下面这两则故事,对于我们正确理解反证法很有帮助.
故事:南方某风水先生到北方看风水,恰逢天降大雪.乃作一歪诗:“天公下雪不下雨,雪到地上变成雨;早知雪要变成雨,何不当初就下雨.”他的歪诗又恰被一牧童听到,亦作一打油诗讽刺风水先生:“先生吃饭不吃屎,饭到肚里变成屎;早知饭要变成屎,何不当初就吃屎.
第一节
点与圆的位置关系
实际上,小牧童正是巧妙运用了反证法,驳斥了风水先生否定事物普遍运动的规律,只强调结果,不要变化过程的形而上学的错误观点:假设风水先生说的是真理,只强调变化最后的结果,不要变化过程也可,那么,根据他的逻辑,即可得出先生当初就应吃屎的茺唐结论.风水先生当然不会承认这个事实了.那么,显然,他说的就是谬论了.
这就是反证法的威力,一个原本非常复杂难证的哲学问题被牧童运用了“以其人之道,还其人之身”的反证法迎刃而解了.
第一节
点与圆的位置关系
下面我们来看这样几个练习加深本节课的学习
【兔爸数学】1.下列说法正确的是( )
A.过一点A的圆的圆心可以是平面上任意点
B.过两点A、B的圆的圆心在一条直线上
C.过三点A、B、C的圆的圆心有且只有一点
D.过四点A、B、C、D的圆不存在
【兔爸数学】2.若△ABC的外接圆的圆心在△ABC的内部,则△ABC是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
【兔爸数学】3.
Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙A的位置关系是( )
A.点D在⊙A外
B.点D在⊙A上
C.点D在⊙A内
D.无法确定
【兔爸数学】4.若AB=4cm,则过点A、B且半径为3cm的圆有______个
第一节
点与圆的位置关系
【兔爸数学】5.用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应该假设这个三角形中( )
A.有一个内角小于60°
B.每一个内角都小于60°
C.有一个内角大于60°
D.每一个内角都大于60°
【兔爸数学】6.在△ABC中,BC=24cm,外心O到BC的距离为6cm,则△ABC外接圆的半径为______.
【兔爸数学】7.已知圆的半径等于5cm,根据下列点P到圆心的距离:
(1)4cm;(2)5cm;(3)6cm,判定点P与圆的位置关系,并说明理由.
【兔爸数学】8.
(教材变式题)如图所示,△ABC中,AB=AC=10,BC=12,求△ABC外接圆的半径.
第一节
点与圆的位置关系
答案:1.B;2.A;3.A;4.
0≤d<3cm;5.D;6.
7.解:(1)当d=4
cm时,∵d<r,∴点P在圆内;
(2)当d=5
cm时,∵d=r,∴点P在圆上;
(3)当d=6
cm时,∵d>r,∴点P在圆外.
8.解:如图,作AD⊥BC,垂足为D,则O一定在AD上,
https://www.21cnjy.com/help/help_extract.php
人教版
九上
第二十四章
圆
第一节
点与圆的位置关系
第一节
点与圆的位置关系
1.上节课我们学习了圆的概念,请同学们回答一下什么是圆?
(在平面内一条线段OA绕着它一个固定的端点O旋转一周,另外一个端点A所形成的图形。)【也可以这样说过定点O等于定长OA的所有点的集合】
我们来看这样一个题目
【兔爸数学】设AB=3cm,作图说明满足下列要求的图形:
(1)到点A和点B的距离都等于2cm的所有点组成的图形;
(2)到点A和点B的距离都小于2cm的所有点组成的图形。
课堂回顾
第一节
点与圆的位置关系
课堂回顾
【做法】
(1)作半径为2cm的圆A;(2)作半径为2cm的圆B;
(3)找出两圆公共部分
【答案】(1)C,D两点;(2)两个圆中CD弧所夹公共部分,即图中黄色区域
第一节
点与圆的位置关系
2.了解什么是圆心,什么是半径,直径,什么是弧,什么是弦、什么是圆心角,什么是圆周角?现在我给大家一个空白纸,大家在这张纸上画出圆,半径,直径,弦,圆周角并标记出来,圆心角;看谁画的又准确又快!
第一节
点与圆的位置关系
圆心:点O
半径:r
直径:d=CD
弦长:EF
任意弧长:
圆周角:
圆心角:
第一节
点与圆的位置关系
3.我们还学习了垂径定理;弦、弧、圆心角的关系以及圆周角和圆心角的关系,是什么呢?你还记得吗?
(垂直于弦的直径平分弦,并且平分弦所对的两条弧---垂径定理)
(在同圆或者等圆中,相等的圆心角所对的弧相等,所对的弦也相等;反过来也可以这样说:在同圆或者等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等;如果两条弦相等,那么他们所对的圆心角相等,所对的弧也相等----弦、弧、圆心角的关系)
(一条弧所得圆周角等于它所对的圆心角的一半,同弧或者等弧所对的圆周角相等,半圆或者直径所对的圆周角是直角,反之直角所对的弦是直径----
圆心角与圆周角的关系)
第一节
点与圆的位置关系
我们通过对上节课的复习对圆的一些基本性质和概念有了更深的印象,这节课我们来学习新知识,点与圆、直线与圆的位置关系,由于时间的问题,我们本节课只完成点与圆的位置关系的学习,请同学们和我一起来看下面这个动画【兔爸数学】2016年秋季学期新人教版九年级上册
24.2.1点和圆的位置关系.swf
给同学们这样一个空白的圆,如图(1)大家根据投掷飞镖的位置,在圆中描点:
讲授新课
描点后的图
第一节
点与圆的位置关系
通过作图描点大家发现了什么呢?如果用数学的语言表达出来又该怎么描述呢?
我们一起来说明,已知圆的的半径为r,我们将这些点到圆心的距离分别记为:a、b、c、d、e
通过标记和比较得出:[a
第一节
点与圆的位置关系
由此我们得出这样的结论:点与圆的位置关系有三种。
(1)当点在圆外时,这个点到圆心的距离____半径;
【大于】
(2)当点在圆上时,这个点到圆心的距离____半径;
【等于】
(3)当点在圆内时,这个点到圆心的距离____半径;
【小于】
通过对点和圆的位置关系的学习,我们来进一步探究这样一个问题:我们知道,已知圆心和半径,可以作一个圆,经过一个已知点A能不能作圆,这样的圆你能作出多少个?经过两个已知点A,B能不能作圆?如果能,圆心分布有什么特点?
概念总结,探究思考
第一节
点与圆的位置关系
作圆的关键是确定圆心和半径的大小,对于经过一个已知点作圆的问题,
首要任务就是确定圆心,圆心确定了,半径也就随之确定了,
那么问题就简单了,经过点A做圆,只要在点A以外任意一点确定为圆心,
圆心与点A的距离为半径作圆即可,我们可以画出图形如下图(3):
探究思考
由此可知经过一个已知点A能作圆,
这样的圆你能作出无数个
第一节
点与圆的位置关系
再来看经过两个点A,B做圆的问题,也就是说圆心到点A和点B的距离相等,那么我们根据以前所学知识知道,到线段两个端点的距离相等的点就是这样一条线即线段AB的垂直平分线,也就是说只要圆心在这条线上,都能满足到点A,B距离相等,如下图(4)所示:
探究思考
经过两个已知点A,B能作圆,
这样的圆也是有无数个的。
第一节
点与圆的位置关系
我们进一步思考:经过不在同一直线上的三点A,B,C能不能作圆?如果能,如何确定所作圆的圆心?如下图所示我们画出图形:
【思路分析】根据题目我们可以这样理解:我们要作这样一个圆能满足点A,B,C都在圆上,也就是说圆心的距离到这三个点的距离相等都等于半径,根据上面我们经过两个点的圆,就在这条线段的垂直平分线上,因此要满足经过三个点,就是说圆心都在这三条线段的垂直平分线上,于是我们连接这三个点,作出这个三角形的三条垂直平分线,作图如下:
探究思考
第一节
点与圆的位置关系
如图,我们作线段AC的垂直平分线为m,做线段BC的垂直平分线为n,做线段AB的垂直平分线为l,三条垂直平分线的交点为点O,由此可以得出OA-OB=OC,即就是说交点O即为圆心,就有OA-OB=OC=OD=r
思考总结
第一节
点与圆的位置关系
由此我们得出这样的结论:不在同一直线的三个点确定一个圆。
如上图中经过三角形ABC的三个顶点可以作一个圆,这个圆叫做三角形的外接圆;外接圆的圆心是这个三角形的三条边的垂直平分线的交点,叫做这个三角形的外心。
我们知道了不在同一直线的三个点可以确定一个圆,那么在同一直线的三个点能确定一个圆吗?(想一想)
第一节
点与圆的位置关系
思考后我们一起来解决,我们不妨假设存在这样的一个圆满足经过这三个点A,B,C,设圆心为点O,那么点O在线段AB的垂直平分线上,也在线段AC的垂直平分线上,同时也在线段BC的垂直平分线上,根据之前所学知识,做出这三个线段的垂直平分线,观察可知三条线段的垂直平分线都相互垂直,这和我们之前所学的过一个点有且只有一条直线与已知直线相互垂直相矛盾,所以这个结论是不成立的,作图如下。
第一节
点与圆的位置关系
上面证明“经过同一条直线上的三个点不能作圆”的方法与我们之前所学过的证明不同,他不是直接从命题的已知得出结论,而是假设命题的结论不成立(即假设经过同一直线上的三个点可以做一个圆),由此经过推理得出矛盾,由此矛盾断定所做假设不正确,从而得到原命题成立,这种方法叫做反证法。
在某种情形下,反证法是很有效的证明方法。例如用反证法证明平行线的性质:“两直线平行,同位角相等”在这里我们就不演示证明过程了,同学们自己思考证明,然后参照课本94页验证自己证明方法是否正确。
第一节
点与圆的位置关系
趣味数学-----反证法
反证法一节,可以说是一个难点.因为以前我们的证明,所采用的方法均为直接证法,由已知到结论,顺理成章.而对于属于间接证法的反证法,许多同学正是难以走出直接证法的局限,从而不能深刻或正确理解反证法思想.其实,反证法作为证明方法的一种,有时起着直接证法不可替代的作用.下面这两则故事,对于我们正确理解反证法很有帮助.
故事:南方某风水先生到北方看风水,恰逢天降大雪.乃作一歪诗:“天公下雪不下雨,雪到地上变成雨;早知雪要变成雨,何不当初就下雨.”他的歪诗又恰被一牧童听到,亦作一打油诗讽刺风水先生:“先生吃饭不吃屎,饭到肚里变成屎;早知饭要变成屎,何不当初就吃屎.
第一节
点与圆的位置关系
实际上,小牧童正是巧妙运用了反证法,驳斥了风水先生否定事物普遍运动的规律,只强调结果,不要变化过程的形而上学的错误观点:假设风水先生说的是真理,只强调变化最后的结果,不要变化过程也可,那么,根据他的逻辑,即可得出先生当初就应吃屎的茺唐结论.风水先生当然不会承认这个事实了.那么,显然,他说的就是谬论了.
这就是反证法的威力,一个原本非常复杂难证的哲学问题被牧童运用了“以其人之道,还其人之身”的反证法迎刃而解了.
第一节
点与圆的位置关系
下面我们来看这样几个练习加深本节课的学习
【兔爸数学】1.下列说法正确的是( )
A.过一点A的圆的圆心可以是平面上任意点
B.过两点A、B的圆的圆心在一条直线上
C.过三点A、B、C的圆的圆心有且只有一点
D.过四点A、B、C、D的圆不存在
【兔爸数学】2.若△ABC的外接圆的圆心在△ABC的内部,则△ABC是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
【兔爸数学】3.
Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙A的位置关系是( )
A.点D在⊙A外
B.点D在⊙A上
C.点D在⊙A内
D.无法确定
【兔爸数学】4.若AB=4cm,则过点A、B且半径为3cm的圆有______个
第一节
点与圆的位置关系
【兔爸数学】5.用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应该假设这个三角形中( )
A.有一个内角小于60°
B.每一个内角都小于60°
C.有一个内角大于60°
D.每一个内角都大于60°
【兔爸数学】6.在△ABC中,BC=24cm,外心O到BC的距离为6cm,则△ABC外接圆的半径为______.
【兔爸数学】7.已知圆的半径等于5cm,根据下列点P到圆心的距离:
(1)4cm;(2)5cm;(3)6cm,判定点P与圆的位置关系,并说明理由.
【兔爸数学】8.
(教材变式题)如图所示,△ABC中,AB=AC=10,BC=12,求△ABC外接圆的半径.
第一节
点与圆的位置关系
答案:1.B;2.A;3.A;4.
0≤d<3cm;5.D;6.
7.解:(1)当d=4
cm时,∵d<r,∴点P在圆内;
(2)当d=5
cm时,∵d=r,∴点P在圆上;
(3)当d=6
cm时,∵d>r,∴点P在圆外.
8.解:如图,作AD⊥BC,垂足为D,则O一定在AD上,
https://www.21cnjy.com/help/help_extract.php
同课章节目录
