多边形的内角和课件
图片预览




文档简介
(共29张PPT)
孝南区车站中学数学组
孝南区车站中学数学组
学 习 目 标
经历探索多边形内角和及外角和公式的过程,并能熟练运用多边形的内角和及外角和公式解决相关问题。
看课本81-82页例2上方的内容,完成学案中填表题,5分钟后比一比哪个小组能正确回答下列问题:
1.多边形的内角和公式是怎样的?
2.课本中是怎样推导这个公式的?
3.你会应用这个公式进行简单的计算吗?
自 学 指 导 一
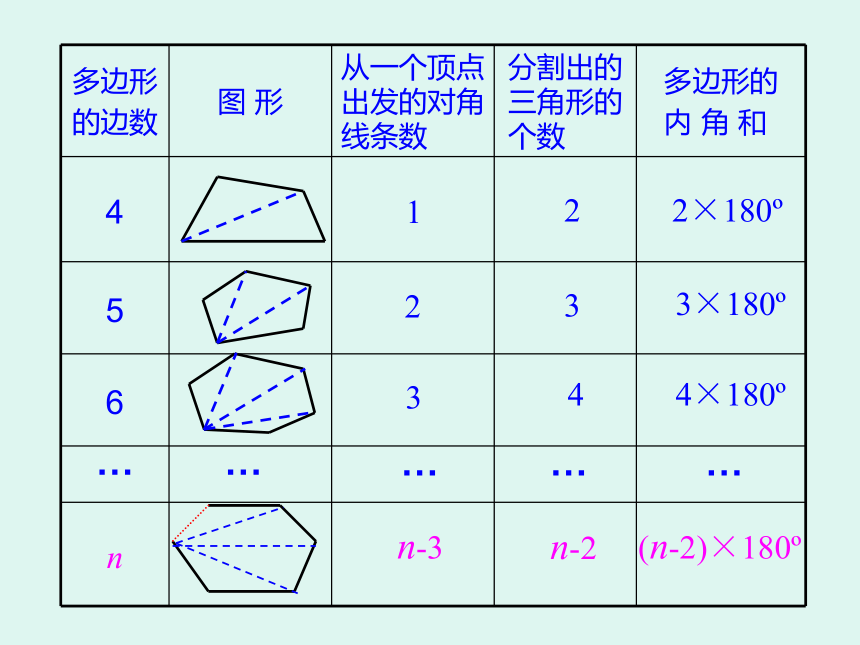
多边形
的边数 图 形 从一个顶点出发的对角线条数 分割出的三角形的个数 多边形的
内 角 和
4
5
6
n
n-2
2
3
2×180
3×180
(n-2)×180
1
2
n-3
…
…
…
…
4
4×180
3
…
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
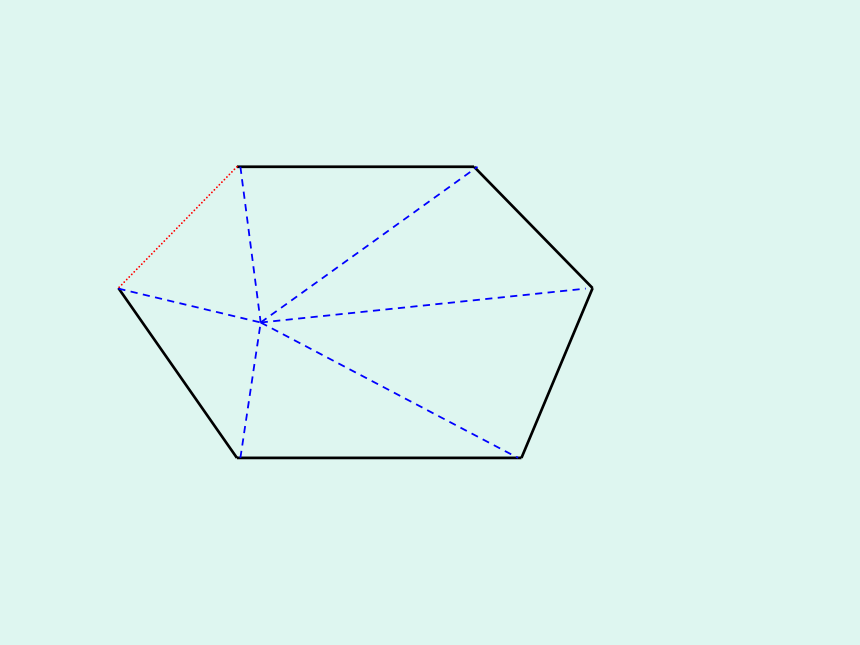
这种分割方式,将多边形分成n个三角形,故所有三角形的内角和为n×180 °,中间一点周围所成的圆周角不是多边形的内角,因此n边形的内角和为 n×180 °- 360 °= (n-2)×180 °
多了什么?如何处理?
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为 (n-1)×180 °- 180 °= (n-2)×180 °
2.根据多边形的内角和求多边形的边数。
1.根据多边形的边数求多边形的内角和。
3.如果四边形的一组对角互补,那么另一组对角有什么关系?
1080o
720o
1440o
多边形的边数
多边形的内角和
5
8
6
10
540o
9
7
12
多边形的内角和
多边形的边数
360o
1260o
900o
1800o
4
看课本82页例2—-83页练习上方的内容,边看边完成学案中的填空题,5分钟后,比一比谁的答案最准确!
自 学 指 导 二
一、如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
180°
180°× 5
180°× ( 5-2 )
180°×5- 180°× ( 5-2 ) =360°
解:∵五边形的每一个外角与它相
邻的内角的和是 ,
∴五边形的内角和加外角和等
于 。
∵五边形的内角和等于
,
∴五边形的外角和等于
。
C
2
A
E
B
3
4
5
1
你能用推理的形式说明多边形的外角和是360°吗?
解:∵ n边形的每一个外角与它
相邻的内角的和是____,
∴ n边形的内角和加外角和
等于 ________。
∵ n 边形的内角和等于
______________,
∴ n 边形的外角和等于
___________________________ 。
A1
A2
A3
An
A4
180°
180°× n
180°× ( n-2 )
180°×n-180°× ( n-2 ) =360°
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。
即:多边形的外角和等于360 。
1.当多边形的边数增加时,它的内角和也
随着增加。 ( )
2.当多边形的边数增加时,它的外角和也随
着增加。 ( )
3.一个多边形的内角中,最多可以有三个锐
角。 ( )
4.将一个长方形的桌面锯去一块后,余下各
内角的和为540°。 ( )
√
√
×
×
1.一个多边形的内角和不可能是( )。
A. 540° B.7200 ° C.1800 ° D.2000 °
2.一个多边形的每一个外角都等于72 ° ,则它的边数是( )。
A.四 B.五 C.六 D.八
3.一个正多边形的一个内角为120 °,则它的边数是
( )。
A.四 B.五 C.六 D.八
4.正十边形的每一个内角的度数都是( )。
A. 120 ° B.135 ° C.144 ° D.180 °
D
B
C
C
求下列图形中x的值:
(1)
C
A
B
D
E
AB∥CD
(2)
如图,小明从O点出发,前进5米后向右转,再前进5米后又向右转,……,这样一直走下去,他第一次回到出发点O时一共走了( )米。
A.60米 B.100米 C.90米 D.120米
C
20o
20o
O
你能帮小亮计算出图中∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数吗?
∠A+∠B+∠C+∠D+∠E+∠F+∠G=
540°
A
B
E
F
G
C
D
1
2
3
4
学 习 目 标
经历探索多边形内角和及外角和公式的过程,并能熟练运用多边形的内角和及外角和公式解决相关问题。
课 后 作 业
1.课本85页4、5、6题。
2.练习册一课时。
孝南区车站中学数学组
孝南区车站中学数学组
学 习 目 标
经历探索多边形内角和及外角和公式的过程,并能熟练运用多边形的内角和及外角和公式解决相关问题。
看课本81-82页例2上方的内容,完成学案中填表题,5分钟后比一比哪个小组能正确回答下列问题:
1.多边形的内角和公式是怎样的?
2.课本中是怎样推导这个公式的?
3.你会应用这个公式进行简单的计算吗?
自 学 指 导 一
多边形
的边数 图 形 从一个顶点出发的对角线条数 分割出的三角形的个数 多边形的
内 角 和
4
5
6
n
n-2
2
3
2×180
3×180
(n-2)×180
1
2
n-3
…
…
…
…
4
4×180
3
…
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
这种分割方式,将多边形分成n个三角形,故所有三角形的内角和为n×180 °,中间一点周围所成的圆周角不是多边形的内角,因此n边形的内角和为 n×180 °- 360 °= (n-2)×180 °
多了什么?如何处理?
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
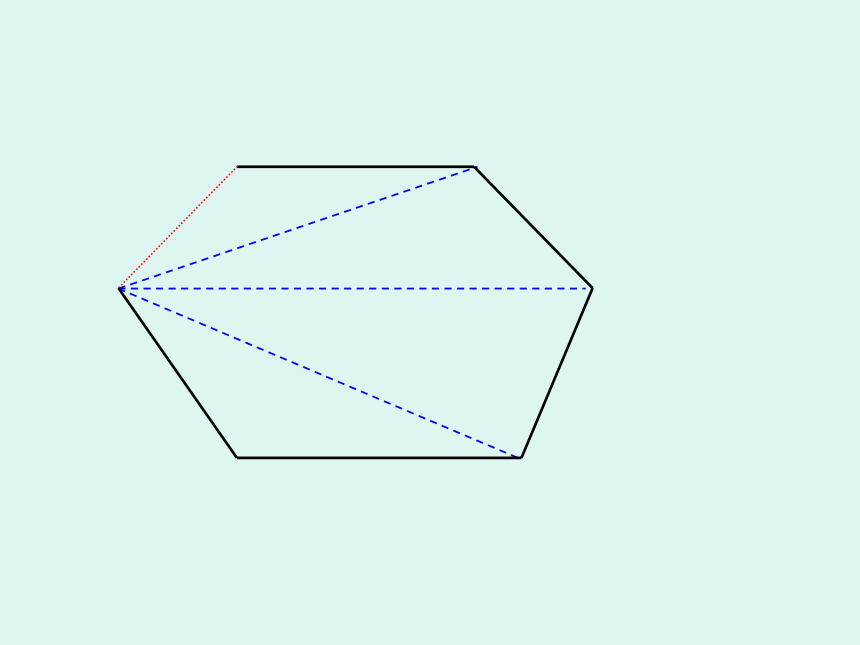
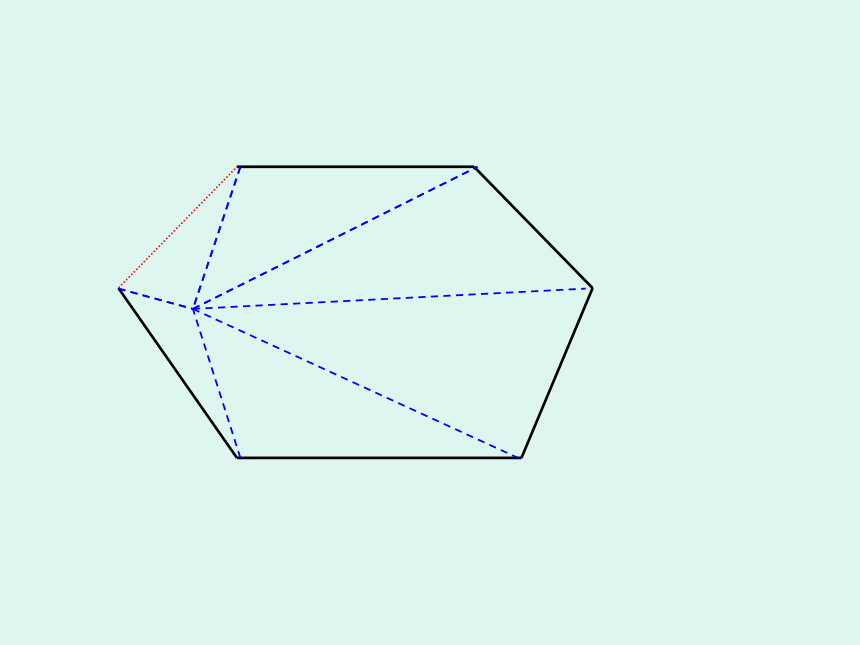
这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为 (n-1)×180 °- 180 °= (n-2)×180 °
2.根据多边形的内角和求多边形的边数。
1.根据多边形的边数求多边形的内角和。
3.如果四边形的一组对角互补,那么另一组对角有什么关系?
1080o
720o
1440o
多边形的边数
多边形的内角和
5
8
6
10
540o
9
7
12
多边形的内角和
多边形的边数
360o
1260o
900o
1800o
4
看课本82页例2—-83页练习上方的内容,边看边完成学案中的填空题,5分钟后,比一比谁的答案最准确!
自 学 指 导 二
一、如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
180°
180°× 5
180°× ( 5-2 )
180°×5- 180°× ( 5-2 ) =360°
解:∵五边形的每一个外角与它相
邻的内角的和是 ,
∴五边形的内角和加外角和等
于 。
∵五边形的内角和等于
,
∴五边形的外角和等于
。
C
2
A
E
B
3
4
5
1
你能用推理的形式说明多边形的外角和是360°吗?
解:∵ n边形的每一个外角与它
相邻的内角的和是____,
∴ n边形的内角和加外角和
等于 ________。
∵ n 边形的内角和等于
______________,
∴ n 边形的外角和等于
___________________________ 。
A1
A2
A3
An
A4
180°
180°× n
180°× ( n-2 )
180°×n-180°× ( n-2 ) =360°
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。
即:多边形的外角和等于360 。
1.当多边形的边数增加时,它的内角和也
随着增加。 ( )
2.当多边形的边数增加时,它的外角和也随
着增加。 ( )
3.一个多边形的内角中,最多可以有三个锐
角。 ( )
4.将一个长方形的桌面锯去一块后,余下各
内角的和为540°。 ( )
√
√
×
×
1.一个多边形的内角和不可能是( )。
A. 540° B.7200 ° C.1800 ° D.2000 °
2.一个多边形的每一个外角都等于72 ° ,则它的边数是( )。
A.四 B.五 C.六 D.八
3.一个正多边形的一个内角为120 °,则它的边数是
( )。
A.四 B.五 C.六 D.八
4.正十边形的每一个内角的度数都是( )。
A. 120 ° B.135 ° C.144 ° D.180 °
D
B
C
C
求下列图形中x的值:
(1)
C
A
B
D
E
AB∥CD
(2)
如图,小明从O点出发,前进5米后向右转,再前进5米后又向右转,……,这样一直走下去,他第一次回到出发点O时一共走了( )米。
A.60米 B.100米 C.90米 D.120米
C
20o
20o
O
你能帮小亮计算出图中∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数吗?
∠A+∠B+∠C+∠D+∠E+∠F+∠G=
540°
A
B
E
F
G
C
D
1
2
3
4
学 习 目 标
经历探索多边形内角和及外角和公式的过程,并能熟练运用多边形的内角和及外角和公式解决相关问题。
课 后 作 业
1.课本85页4、5、6题。
2.练习册一课时。
